Презентация « Отбор корней в тригонометрических уравнениях на числовой окружности по материалам открытого банка задач ЕГЭ по математике 2017 года»

МОУ «Гимназия №1»

города Железногорска, Курской области

Отбор корней в тригонометрических уравнениях на числовой окружности по материалам открытого банка задач ЕГЭ по математике 2017 года

учитель математики Р. И. Пискарева

ЕГЭ по математике направлен на контроль сформированности математических компетенций, предусмотренных требованиями Федерального компонента государственного образовательного стандарта среднего (полного) общего образования по математике (2004 г.) Варианты КИМ составлены на основе кодификаторов элементов содержания и требований к уровню подготовки выпускников общеобразовательных учреждений для проведения в 2017 году ЕГЭ по математике. Некоторые задания №13 ЕГЭ по математике (профильный уровень ) представляют собой тригонометрическое уравнение. В последние годы составители заданий ЕГЭ по математике в качестве задания №13 предлагают не сложные тригонометрические уравнения, в демоверсии по математики 2017 года (профильный уровень), задание №13 имеет следующее содержание

а) Решите уравнение

б) Найти все корни этого уравнения принадлежащие промежутку

Задания имеют некоторые особенности. Особенности этого задания в том, что требуется во-первых решить (то есть, найти решения, причём все) во вторых, осуществит отбор решений по тому или иному ограничению.

При отборе можно проверить знания основных разделов школьной математики, уровень логического мышления, навыки исследовательской деятельности.

В анализе типичных ошибок участников ЕГЭ 2016 года И. В. Ященко, А.В. Семёнов и другие отмечают следующее: в 2016 году произошел заметный рост выполнения задания повышенного уровня сложности с развёрнутым ответом №13- решение тригонометрического уравнения с отбором корней.

Если в 2015 г. верно решили - 27,4% , то в 2016 г.- 38,9%

Выполнение второй части задания №13 - это отбор корней принадлежащих заданному промежутку.

Существуют разные способы отбора корней в тригонометрических уравнениях:

• Арифметический способ.
• Перебор значений целочисленного параметра и вычисление корней.
• Функционально - графический способ.
• Отбор корней тригонометрического уравнения, на числовой прямой.
• Отбор корней тригонометрического уравнения на числовой окружности и другие способы.

В процессе обучения решению задач, в которых требуется отобрать корни тригонометрического уравнения, следует обсудить разные способы выполнения этого задания, Во-первых в этом случае выпускники начинают применять знания в нестандартной ситуации, развивается логическое мышление, формируются навыки исследовательской деятельности.

Во – вторых ученик научится выяснять случаи, когда тот или иной способ может оказаться наиболее удобным или наоборот непригодным.

Рассмотрим отбор корней тригонометрического уравнения на числовой окружности.

• Когда удобно применять этот метод.

Этот метод удобно применять, если уравнение имеет несколько корней, объединить которые в один корень невозможно.

Когда корни тригонометрического уравнения, содержат обратные тригонометрические функции.

2 . Что надо уметь и знать, чтобы отобрать корни на числовой окружности.

• Движение начинается от нуля., если корень положительный , то против часовой стрелки, если отрицательный , то по часовой стрелки.

• Числовая окружность по положительному направлению и т.д.
• По отрицательному направлению и т.д.

• Поэтому, если дают числовой промежуток , его надо записать в другом виде или если предлагают промежуток ) , значит надо записать в виде )

0 Через точку первой четверти уметь вычислить симметричные точки в остальных четвертях. " width="640"

• Знать главные части числовой окружности по положительному направлению: ; π ; , по отрицательному ; -π ;

• Знать точки первой четверти, обозначим их буквой t , это табличное значение : (близкое к нулю) , (середина дуги первой четверти), (близкое к ),если это не табличные значения , arcsin a ; arccos a ; arctg a;

arcctg a , где а 0

• Через точку первой четверти уметь вычислить симметричные точки в остальных четвертях.

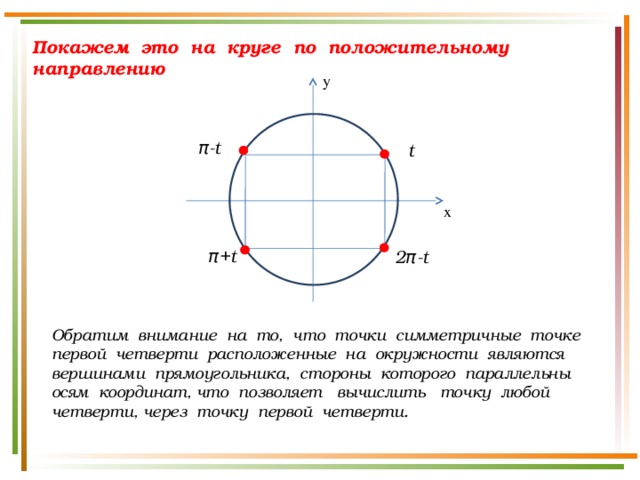
Покажем это на круге по положительному направлению

y

π-t

t

x

π+t

2 π-t

Обратим внимание на то, что точки симметричные точке первой четверти расположенные на окружности являются вершинами прямоугольника, стороны которого параллельны осям координат, что позволяет вычислить точку любой четверти, через точку первой четверти.

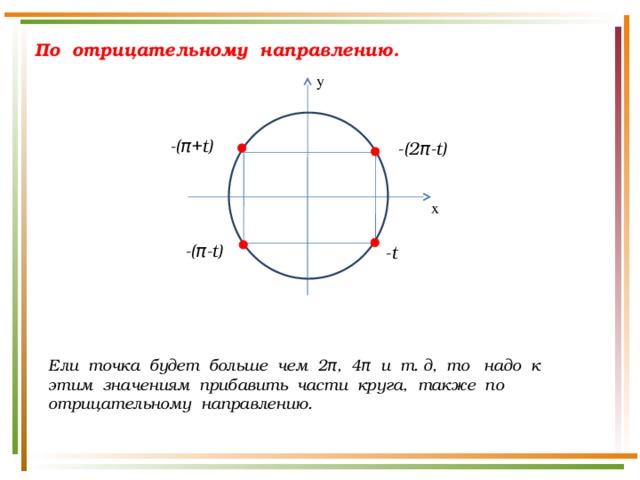
По отрицательному направлению.

y

-(π+t)

-(2 π-t)

x

-(π-t)

-t

Ели точка будет больше чем 2π, 4π и т. д, то надо к этим значениям прибавить части круга, также по отрицательному направлению.

3. Как отбирают корни на числовой окружности.

• Изобразить числовую окружность и на ней чёрными точками отметить все корни тригонометрического уравнения (подписывать корни не надо )

• Изобразить числовую прямую, на которой отметить числовой промежуток (его обязательно заштриховать), обратить внимание на изображение концов промежутка

• Отметить ноль , его расположение зависит от отмеченного промежутка (он может располагаться справа от промежутка, слева и находится внутри промежутка)

• От нуля отмети 2π, 4π, 6π и т, д. или --2π,-4π, -6π и т , д. до конца промежутка.

• Начинаем одновременно двигаться от нуля по числовой прямой и по окружности , если на числовой прямой участок по которому движемся не заштрихован , то точки ( корни уравнения не принадлежат промежутку), если корень попадает в заштрихованный промежуток, то его записываем рядом с точкой изображающей корень уравнения на окружности.

• Если корень принадлежит промежутку меньше круга то, это часть круга вычисляем эту часть (корень уравнения) через точку первой четверти

• Если это больше круга то, надо к целому количеству кругов ( 2π или 4π и т. д. прибавит часть круга до отмеченного корня.

4.Что позволяет изображение числовой прямой?

Во-первых понять в коком направлении двигаться.

Во-вторых увидеть , какие точки числовой окружности (корни уравнения не принадлежат заданному промежутку)

В-третьих правильно вычислить корни уравнения, принадлежащие заданному промежутку.

Приведем примеры решения тригонометрических уравнений и отбора корней , принадлежащих заданному промежутку на числовой окружности.

Пример 1

а) Решите уравнение

б) Укажите корни, принадлежащие промежутку

Решение.

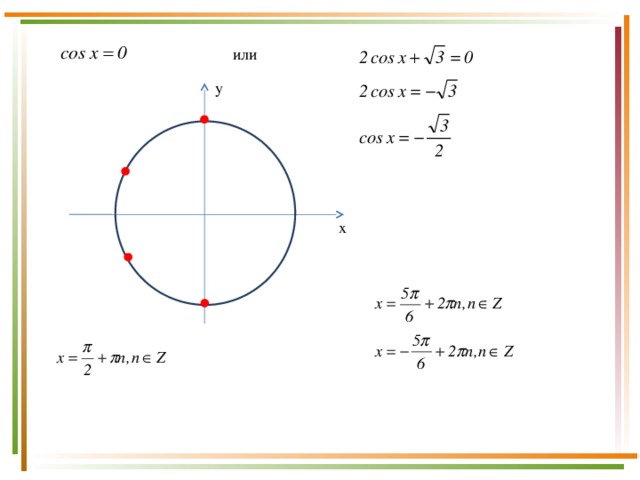
или

y

x

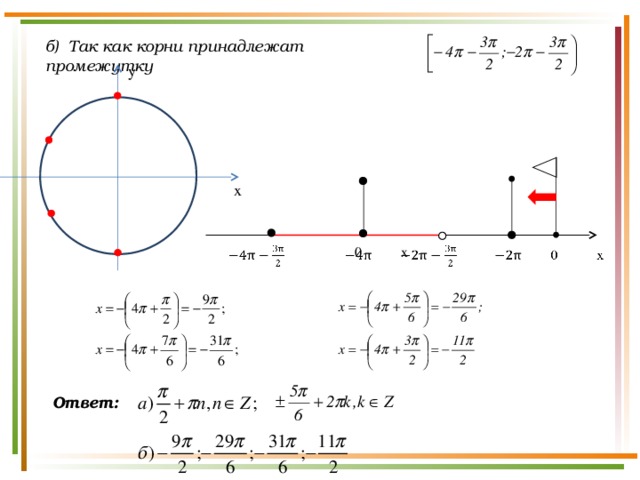
б) Так как корни принадлежат промежутку

y

x

0 х

Ответ:

Пример 2

а) Решите уравнение

б) Укажите корни, принадлежащие промежутку

Решение.

Уравнение равносильно системе

y

1) ОДЗ:

x

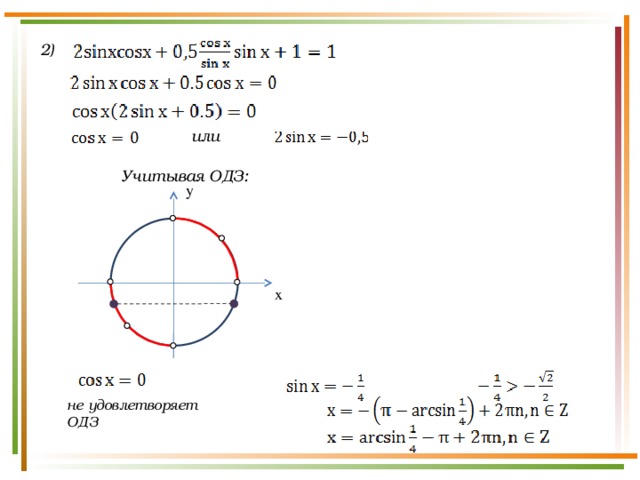
2)

или

Учитывая ОДЗ:

y

x

не удовлетворяет ОДЗ

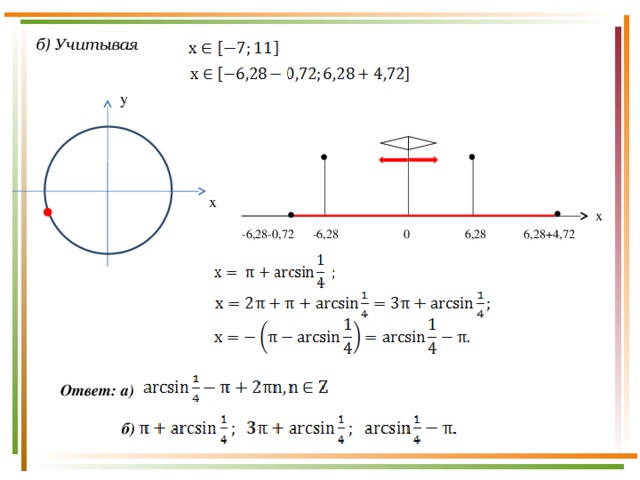
б) Учитывая

y

x

х

-6,28-0,72 -6,28 0 6,28 6,28+4,72

Ответ: а)

б)

Пример 3

а) Решите уравнение

б) Укажите корни, принадлежащие промежутку

Решение.

Пусть

у

t

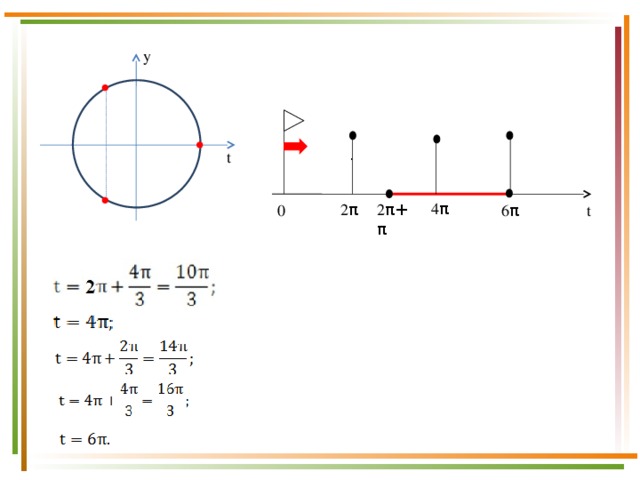
у

t

.

4 π

2 π

2 π+π

t

0

6 π

;

Так как t=2x, то

а)

б)

Ответ: а)

б)

Можно было решить уравнение, методом разложения на множители, применив формулу разность косинусов.

Получим корни:

y

объединив ответы

x

и отобрав корни, принадлежащие

промежутку через круг:

.

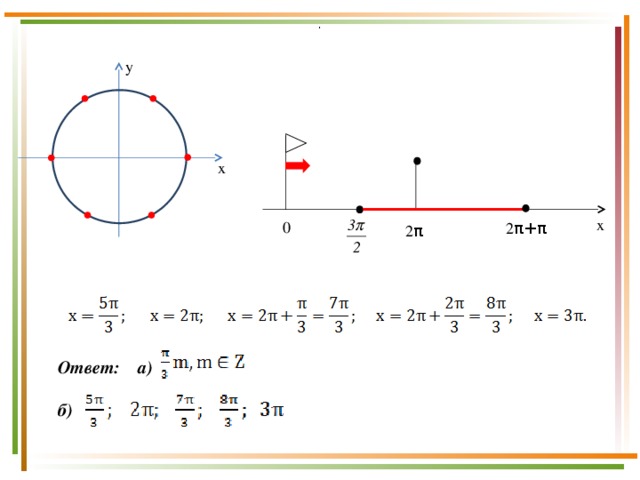
у

x

x

0

2 π+π

2 π

Ответ: а)

б)

Задания для самостоятельного решения