Презентация по геометрии "Правильные и полуправильные многогранники"

Государственное автономное профессиональное образовательное учреждение

«Елабужский колледж культуры и искусств»

преподаватель математики и информатики

Лопанова Любовь Александровна

ПРАВИЛЬНЫЕ И ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ

Все время, когда мы имеем дело с формой, размером, положением предмета в пространстве, мы вовлечены в геометрию. Когда доисторические люди занимались ткачеством или отделкой зданий, они пользовались геометрией, не зная ее. Древним египтянам была нужна геометрия, чтобы измерить участки земли, подвергавшиеся затоплению во время разливов Нила. Им была нужна  геометрия в строительных целях, когда религия заставила их строить могилы для умерших — пирамиды. Само слово «геометрия» произошло от греческих слов «Земля» и «измерять» и, вероятно, является переводом египетского слова.

Геометрические знания примерно в объеме современного курса средней школы были изложены еще 2200 лет назад в “Началах” Евклида. Конечно, изложенная в “Началах” наука геометрия не могла быть создана одним ученым. Известно, что Евклид в своей работе опирался на труды десятков предшественников, среди которых были Фалес и Пифагор, Демокрит и Гиппократ, Архит, Теэтет, Евдокс и др.

Архимед

(287-212 гг до н.э.)

Фалес

(625-546 гг до н.э.)

Теэтет

(417-369 гг до н.э.)

Демокрит

(460-370 гг до н.э.)

Архит

Пифагор

Гиппократ

Евдокс

(564-473 гг до н.э.)

(460-370 гг до н.э.)

(408-355 гг до н.э.)

(428-347 гг до н.э.)

Начала Евклида. «…в науке нет царского пути»

Историческая заслуга Евклида состоит в том, что он, создавая свои “Начала”, объединил результаты своих предшественников, упорядочил и привел в одну систему основные геометрические знания того времени.

«Начала» (в оригинале «Стохейа») состоят из 13 книг, позднее к ним были прибавлены ещё 2.

Первые шесть книг посвящены планиметрии. Книги VII – X содержат теорию чисел, XI, XII и XIII книги «Начал» посвящены стереометрии.

Из постулатов Евклида видно, что он представлял пространство как пустое, безграничное, изотропное и трёхмерное.

около 365 – 300 гг. до н.э.

Интересно, что «Начала» Евклида открываются описанием построения правильного треугольника и заканчиваются изучением пяти правильных многогранных тел! В наше время они известны как Платоновы тела.

Учение о правильных многогранниках, содержащееся в последней XIII книге Евклида, является венцом его «Начал».

Сначала Евклид устанавливает существование этих многогранников, показывает как вписать их в сферу.

После этого Евклид доказывает в 18-м, последнем предложении XIII книги, что, кроме упомянутых пяти тел, нет других правильных многогранников.

ПРАВИЛЬНЫЕ МНОГОГРАННИКИ

Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.

Существует пять типов правильных выпуклых многогранников:

• правильный тетраэдр,
• куб (гексаэдр),
• октаэдр,
• додекаэдр,
• икосаэдр.

Не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и, вообще, n-угольники при n ≥6.

Платон

Платон (Platon) - греческий философ из Афин. Настоящее имя Платона было Аристокл. Прозвище Платон (Широкоплечий) было ему дано в молодости за мощное телосложение. Происходил из знатного рода и получил прекрасное образование. Возможно, слушал лекции гераклитика Кратила, знал популярные в Афинах сочинения Анаксагора, был слушателем Протагора и других софистов. В 407 г. стал учеником Сократа, что определило всю его жизнь и творчество.

около 429 – 347 гг до н.э.

Платоновыми телами называются правильные однородные выпуклые многогранники , то есть выпуклые многогранники, все грани и углы которых равны, причем грани - правильные многоугольники.

Платоновы тела - трехмерный аналог плоских правильных многоугольников. Однако между двумерным и трехмерным случаями есть важное отличие: существует бесконечно много различных правильных многоугольников, но лишь пять различных правильных многогранников.

Правильные многогранники называют также «платоновыми телами» - они занимали видное место в идеалистической картине мира древнегреческого философа Платона.

тетраэдр (от греческих слов «тетра» — четыре и (h)edra — грань);

гексаэдр («гекса» — шесть);

октаэдр («окто» — восемь);

додекаэдр («додека» — двенадцать);

икосаэдр («икоси» — двадцать).

Платоновы тела

куб

додекаэдр

октаэдр

икосаэдр

тетраэдр

вода

воздух

огонь

«всё сущее»

земля

Олицетворение многогранников

Тетраэдр – четырехгранник, все грани которого треугольники, т.е. треугольная пирамида; правильный тетраэдр ограничен четырьмя равносторонними треугольниками.

Так как вершина устремлена вверх его олицетворяли с огнем.

тетраэдр-огонь

Олицетворение многогранников

Гексаэдр (куб) – шестигранник (из шести квадратов). Каждая из 8 вершин куба является вершиной 3 квадратов, поэтому сумма углов при вершине равна 180 0

Куб олицетворял землю, как самый устойчивый многогранник.

куб-земля

Олицетворение многогранников

Октаэдр – восьмигранник, гранями которого являются правильные треугольники и в каждой вершине сходится 4 грани.

Олицетворял воздух, как самый воздушный.

октаэдр-воздух

Олицетворение многогранников

Икосаэдр – двадцатигранник. Каждая вершина икосаэдра является вершиной пяти треугольников.

Следовательно, сумма плоских углов при каждой вершине равна 300 0 .

Олицетворял воду, как самый обтекаемый.

икосаэдр-вода

Олицетворение многогранников

Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.

Додекаэдр – двенадцатигранник. Каждая вершина является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324 0 .

додекаэдр-вселенная

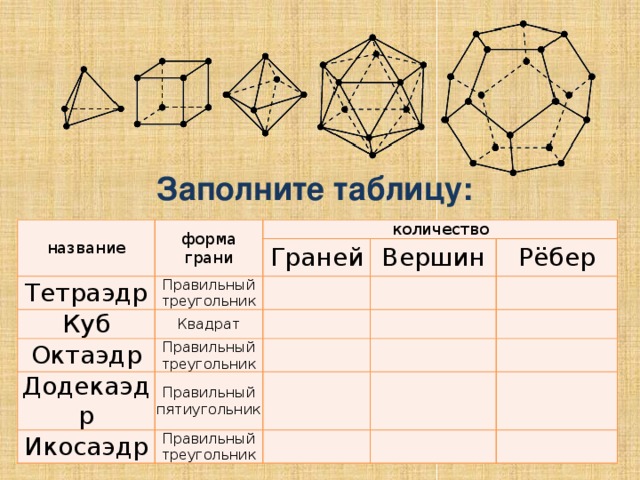
Заполните таблицу:

название

форма грани

Тетраэдр

количество

Куб

Граней

Правильный треугольник

Вершин

Квадрат

Октаэдр

Рёбер

Додекаэдр

Правильный треугольник

Икосаэдр

Правильный пятиугольник

Правильный треугольник

7

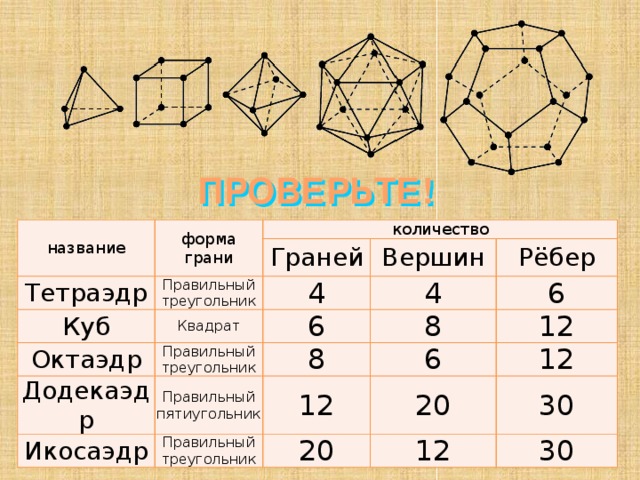
ПРОВЕРЬТЕ!

название

форма грани

Тетраэдр

количество

Куб

Граней

Правильный треугольник

Квадрат

Вершин

4

Октаэдр

Додекаэдр

6

4

Рёбер

Правильный треугольник

8

Икосаэдр

6

Правильный пятиугольник

8

12

12

Правильный треугольник

6

20

12

20

30

12

30

Леонард Эйлер

Один из величайших математиков мира, работы которого оказали решающее влияние на развитие многих современных разделов математики.

Леонард Эйлер доказал теорему

о связи количества граней, вершин и рёбер

правильного многогранника:

Г + В = Р + 2

А позднее он показал, что эта теорема выполняется

для любого выпуклого многогранника .

1707-1783 г.г.

Теорема Эйлера:

Число вершин - число ребер + число граней =2

Архимед Сиракузский

Математик, физик и инженер Архимед Сиракузский оставил после себя немало изобретений, тринадцать сочинений (таких как «О сфере и цилиндре», «Измерение круга», «Равновесие плоскостей», «Стомахион», «Правильный семиугольник и другие).

Архимед, как геометр определил поверхность шара и его объём, исследовал параболоиды и гиперболоиды, изучал «архимедову спираль», определил число «пи», как находящееся между 3,141 и 3,142.

Вклад Архимеда в теорию многогранников - описание 13 полуправильных выпуклых однородных многогранников (архимедовых тел).

около 287 – 212 гг. до н.э.

Архимеду принадлежит открытие тринадцати так называемых полуправильных многогранников («архимедовых тел»)

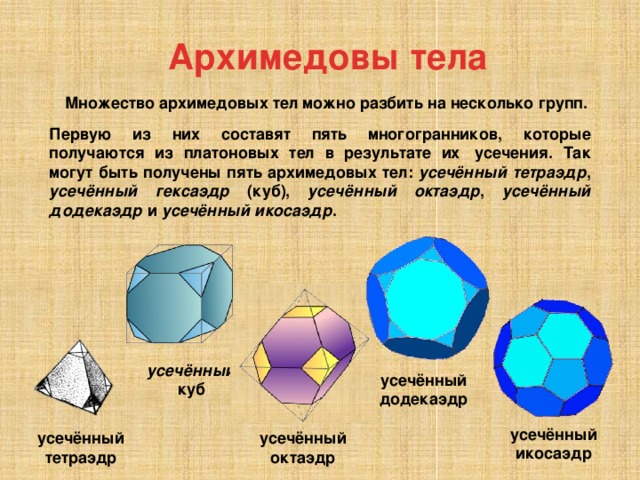
Архимедовы тела

Множество архимедовых тел можно разбить на несколько групп.

Первую из них составят пять многогранников, которые получаются из платоновых тел в результате их  усечения. Так могут быть получены пять архимедовых тел: усечённый тетраэдр , усечённый гексаэдр (куб), усечённый октаэдр , усечённый додекаэдр и усечённый икосаэдр .

усечённый куб

усечённый додекаэдр

усечённый икосаэдр

усечённый тетраэдр

усечённый октаэдр

Архимедовы тела

Другую группу составляют всего два тела, именуемых также квазиправильными многогранниками. Эти два тела носят названия: кубооктаэдр и икосододекаэдр

кубооктаэдр

икосододекаэдр

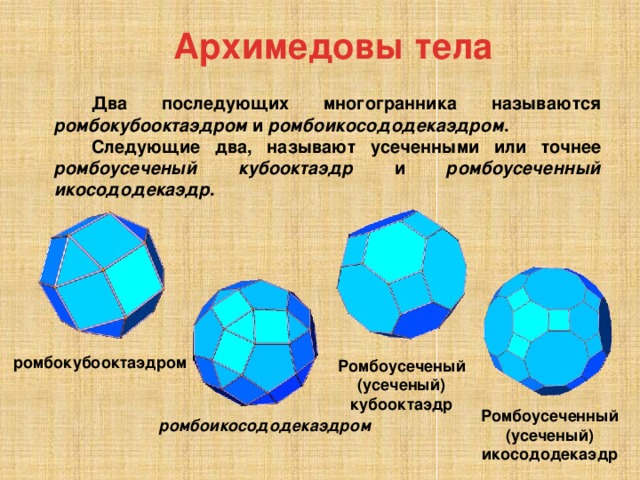
Архимедовы тела

Два последующих многогранника называются ромбокубооктаэдром и ромбоикосододекаэдром .

Следующие два, называют усеченными или точнее ромбоусеченый кубооктаэдр и ромбоусеченный икосододекаэдр .

ромбокубооктаэдром

Ромбоусеченый

(усеченый) кубооктаэдр

Ромбоусеченный

(усеченый) икосододекаэдр

ромбоикосододекаэдром

Архимедовы тела

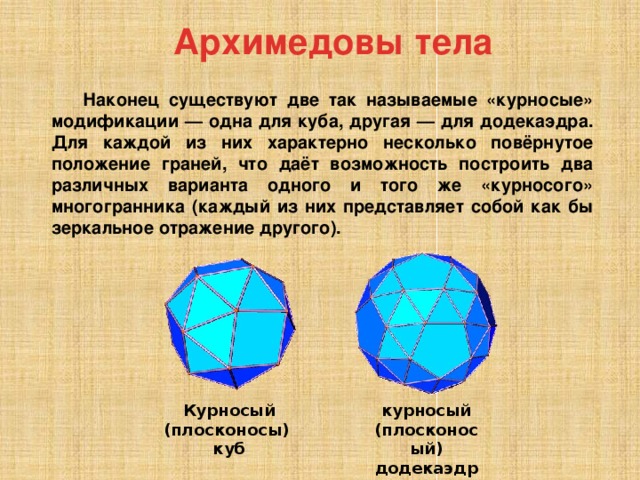
Наконец существуют две так называемые «курносые» модификации — одна для куба, другая — для додекаэдра. Для каждой из них характерно несколько повёрнутое положение граней, что даёт возможность построить два различных варианта одного и того же «курносого» многогранника (каждый из них представляет собой как бы зеркальное отражение другого).

курносый (плосконосый)

додекаэдр

Курносый (плосконосы)

куб

ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ

Выпуклый многогранник называется полуправильным, если его гранями являются правильные многоугольники, возможно, с разным числом сторон, и все многогранные углы равны, причем одни из них в другой можно перевести движением самого многогранника.

Кроме «архимедовых тел» к полуправильным многогранникам относятся правильные n-угольные призмы , все ребра которых равны, и, так называемые, антипризмы с равными ребрами.

Существование нового «архимедова тела» -

Псевдоромбокубооктаэдра ,

который получается из ромбокубооктаэдра поворотом его верхней восьмиугольной «крышки» на 45 градусов по оси – открыл Миллер в 1930 г. и независимо от него В.Г.Ашкинузе и Л.Есаулова. Оба советских математика получили свои результаты независимо друг от друга и от Миллера.

Звездчатые многогранники

Правильные невыпуклые многогранники, полученные из правильных многогранников продолжением граней и ребер.

Иоганн Кеплер

Немецкий астроном и математик. Один из создателей современной астрономии.

Вклад Кеплера в теорию многогранника - это, восстановление математического содержания утерянного трактата Архимеда о полуправильных выпуклых однородных многогранниках.

(1571 – 1630)

Космологическая гипотеза Кеплера

Весьма оригинальна космологическая гипотеза Кеплера, в которой он попытался связать некоторые свойства Солнечной системы со свойствами правильных многогранников. Кеплер предположил, что расстояния между шестью известными тогда планетами выражаются через размеры пяти правильных выпуклых многогранников (Платоновых тел).

Между каждой парой "небесных сфер", по которым, согласно этой гипотезе, вращаются планеты, Кеплер вписал одно из Платоновых тел. Вокруг сферы Меркурия , ближайшей к Солнцу планеты, описан октаэдр . Этот октаэдр вписан в сферу Венеры , вокруг которой описан икосаэдр. Вокруг икосаэдра описана сфера Земли , а вокруг этой сферы - додекаэдр . Додекаэдр вписан в сферу Марса , вокруг которой описан тетраэдр . Вокруг тетраэдра описана сфера Юпитера , вписанная в куб . Наконец, вокруг куба описана сфера Сатурна .

Позже, с открытием еще трех планет и более точным измерением расстояний, эта гипотеза была полностью отвергнута.

Звездчатый октаэдр

Восемь пересекающихся плоскостей граней октаэдра отделяют от пространства новые «куски», внешние по отношению к октаэдру. Это малые тетраэдры основания которые совпадают с гранями октаэдра.

Можно рассматривать как соединение двух пересекающихся тетраэдров центры которых совпадают с центром исходного октаэдра. Все вершины звездчатого октаэдра совпадают с вершинами некоторого куба, а ребра его являются диагоналями граней (квадратов) этого куба. Дальнейшее продление граней октаэдра не приводит к созданию нового многогранника. Октаэдр имеет только одну звездчатую форму. Такой звездчатый многогранник открыл еще Леонардо да Винчи, затем спустя почти 100 лет в 1619 году описал Кеплер и назвал его Stella octangula - восьмиугольная звезда .

Тела Кеплера-Пуансо

Иоганн Кеплер, для которого правильные многогранники были любимым предметом изучения, в своем первом его крупном сочинении «Mysterium Cosmographicum» — «Космографическая тайна» (1596 г.) развил учение о двух видах выпуклых звездчатых многогранников (которые получаются из правильных многогранников продолжением граней или рёбер).

Большой звездчатый додекаэдр – получается при продолжении граней додекаэдра, при этом каждая грань заменяется на правильный звездчатый пятиугольник. Его можно также получить из икосаэдра, установкой на его гранях правильных треугольных пирамид.

Малый звездчатый додекаэдр – образован продолжением граней выпуклого додекаэдра. Этот многогранник можно получить из додекаэдра, установкой на его гранях правильных пятиугольных пирамид.

Тела Кеплера-Пуансо

Луи Пуансо французский математик и механик, Парижской АН с 1813. Окончил Политехническую школу в Париже (1797), с 1809 профессор там же. В период Июльской монархии – в Министерстве народного образования. Пэр Франции (1846), сенатор (1852).

Первые работы Пуансо посвящены теории правильных звездчатых многогранников. В 1803 опубликовал «Элементы статистики», в которых применил разработанные им геометрические методы исследования к учению о равновесии твердых тел и их систем. В начале 1810 открыл существование еще двух видов правильных невыпуклых многогранников.

(1777—1859)

Большой додекаэдр получается при продолжении граней додекаэдра. Его можно так же получить из икосаэдра, вырезанием из его граней правильных треугольных пирамид.

Большой икосаэдр получается при продолжении граней икосаэдра. Его можно так же получить из малого звездчатого додекаэдра, вырезанием из его граней треугольных пирамид.

Правильные звездчатые многогранники

Французский математик, Огюстен Коши в 1812 г, доказал, что возможные правильные многогранники исчерпываются пятью выпуклыми «платоновыми телами» и четырьмя звездчатыми многогранниками Кеплера-Пуансо, к которым можно добавить звездчатый октаэдр Кеплера.

(1789—1857)

малый звездчатый додекаэдр

большой икосаэдр

звездчатый октаэдр

большой звездчатый додекаэдр

большой додекаэдр

Звездчатые кубооктаэдры

Помимо правильных звездчатых многогранников (тел Кеплера-Пуансо) имеется более сотни различных звездчатых форм многогранников. Например звездчатые формы кубооктаэдра:

Звездчатые икосаэдры

Всего звездчатых икосаэдров 59, некоторые из них:

Звездчатые икосододекаэдры

Всего звездчатых икосододекаэдров 19, некоторые из них:

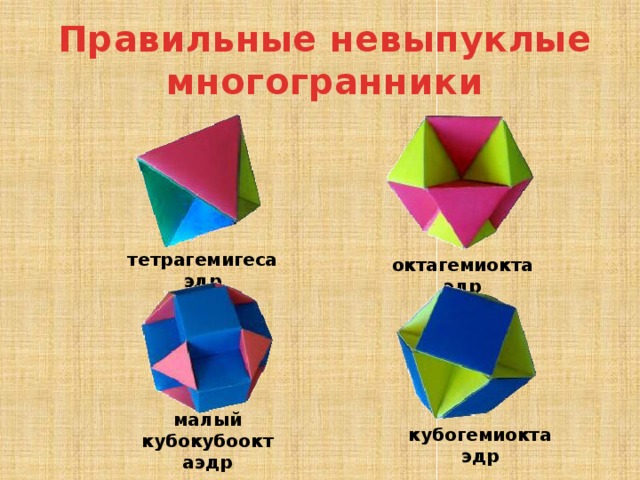
Правильные невыпуклые многогранники

тетрагемигесаэдр

октагемиоктаэдр

малый кубокубооктаэдр

кубогемиоктаэдр

Лука Пачоли

Интерес к правильным многогранникам возродился в эпоху Ренессанса, в частности, в кругах архитекторов и художников. Итальянский математик Лука Пачоли приезжает в Милан, где читает лекции по математике. В Милане в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» в которой рассматривается 59 многогранников, «золотое сечение» и «архимедовы тела».

Блестяще выполненные иллюстрации к книге сделал Леонардо да Винчи. К нескольким рукописным экземплярам трактата, врученным властительным особам, прилагается набор правильных многогранников и других геометрических тел, о которых Лука говорит, что изготовил из собственноручно.

(1445—1517)

Полуправильные многогранники, нарисованные Леонардо да Винчи для книги Пачоли «О божественной пропорции»

Леонардо да Винчи

Титан возрождения, живописец, скульптор, ученый и изобретатель Леонардо да Винчи – символ неразрывности искусства и науки, а следовательно, закономерен его интерес к таким прекрасным, высокосиметричным объектам, как выпуклые многогранники вообще и усеченный икосаэдр в частности

(1452—1519)

Рисунок «Витрувианский человек» символизирует внутреннюю симметрию, Божественную пропорцию человеческого тела. Две наложенные одна на другую фигуры вписаны в круг и квадрат. Этот рисунок определил канонические пропорции изображения человека для европейского искусства.

Мориц Корнилис Эшер

Голландский художник Мориц Корнилис Эшер создал уникальные и очаровательные работы, в которых использованы или показаны широкий круг математических идей.

Правильные геометрические тела – многогранники – имели особое очарование для Эшера. В его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов.

(1898-1972)

На гравюре «Четыре тела» Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.

Мориц Корнилис Эшер

Изящный пример звездчатого додекаэдра можно найти в его работе «Порядок и хаос». В данном случае звездчатый многогранник помещен внутрь стеклянной сферы. Аскетичная красота этой конструкции контрастирует с беспорядочно разбросанным по столу мусором.

В гравюре «Звезды» , на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров. Если бы Эшер изобразил в данной работе лишь различные варианты многогранников, мы никогда бы не узнали о ней. Но он по какой-то причине поместил внутрь центральной фигуры хамелеонов, чтобы затруднить нам восприятие всей фигуры.

Литография «Водопад» , где на вершинах башен изображены разновидности звездчатого многогранника

В картине «Силы гравитации» присутствуют три перпендикулярные друг другу силы гравитации в звездчатом многограннике.

Альбрехт Дюрер

Его считают знаменитейшим и самым блестящим живописцем Германии эпохи возрождения. Воспитанный в мастерской серебряных дел мастера, Альбрехт Дюрер был те только удивительным художником и гравером, но (подобно Микеланджело) он занимался еще архитектурой, скульптурой, музыкой, словесностью.

(1471-1528)

Несколько веков почитатели живописи пытались расшифровать аллегорический ансамбль на знаменитой гравюре на меди «Меланхолия» написанной в 1514 году.

На ней изображена фигура и великое множество разных предметов, а на самом видном месте – геометрический многогранник – ромбоэдр с усеченными вершинами. Но символом чего он является? Ведь не случайно же Дюрер – сын ювелира, уделил ему столько внимания? Догадка напрашивается сама собой помещенный на самое видное место кристалл – символ и идеального слияния форм и гглубокого содержания, символ порядка и гармонии. В 1973 году было доказано, что это флюорит плавиковый шпат CaF 2, широко распространенный и используемый для изготовления брошей и колец.

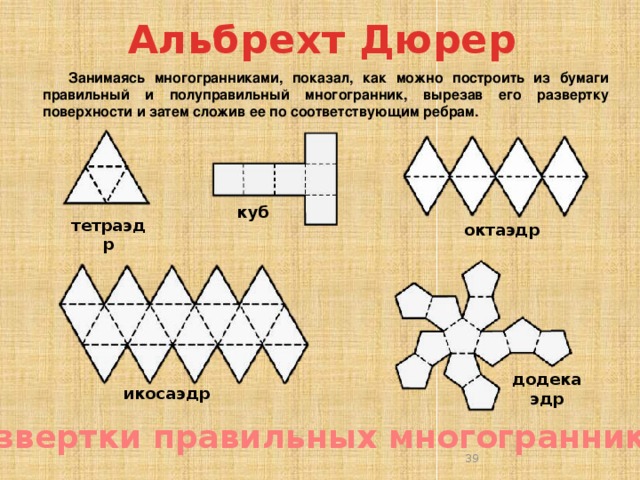
Альбрехт Дюрер

Занимаясь многогранниками, показал, как можно построить из бумаги правильный и полуправильный многогранник, вырезав его развертку поверхности и затем сложив ее по соответствующим ребрам.

куб

тетраэдр

октаэдр

додекаэдр

икосаэдр

Развертки правильных многогранников

Правильные многогранники в искусстве

Сальвадор Дали на картине «Тайная вечеря» изобразил Иисуса Христа со своими учениками на фоне огромного прозрачного додекаэдра

Интарсия – вид декоративного искусства, выполняемая деревом по дереву. Мозаики созданные Фра Джовани да Верона (1457 – 1525), созданные для церкви Santa Maria in Organo в Вероне.

Художница Суламифь Вулфинг (Sulamith Wulfing), родившаяся в Германии (1901 – 1989), своими картинами открывает мистический мир, где присутствуют добро и зло, феи, ангелы, драконы. Благодаря своей развитой интуиции художница сумела почувствовать форму энергетической оболочки человека в почти правильном виде, что отражено на ее картине «Христос-Младенец», где центральная фигура Христа находится внутри Икосаэдра.

Правильные многогранники

в живой природе

Вирус полиомиелита имеет форму додекаэдра . Он может жить и размножаться только в клетках человека и приматов.

Феодария

Бактериофаг Т4

Скелет одноклеточного организма феодарии по форме напоминает икосаэдр

Вирус поражающий сенные растения типа помидоров и огурцов (точнее, внешняя белковая оболочка вируса). Практически, усеченный икосаэдр .

вирус ветряной

оспы

вирус краснухи

Вирусы

Правильные многогранники в газах

Фуллерены – класс химических соединений, молекулы которых состоят только из углерода, число атомов которого четно, от 32 и более 500, они представляют по структуре выпуклые многогранники, построенные из правильных пяти- и шестиугольников.

Разнообразие физико-химических и структурных свойств соединений на основе фуллеренов позволяет говорить о химии фуллеренов как о новом, перспективном направлении органической химии.

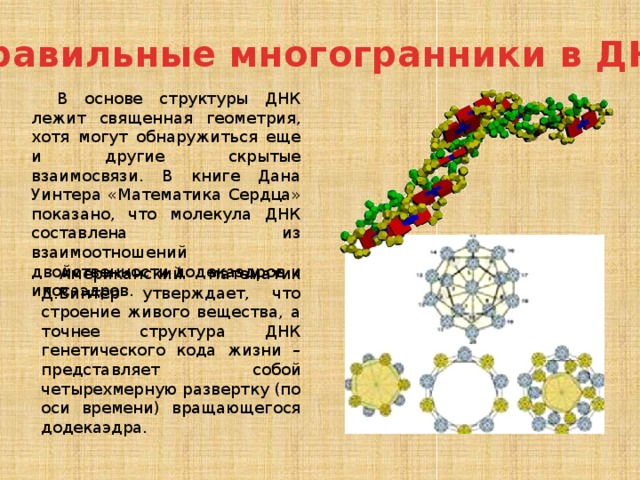
Правильные многогранники в ДНК

В основе структуры ДНК лежит священная геометрия, хотя могут обнаружиться еще и другие скрытые взаимосвязи. В книге Дана Уинтера «Математика Сердца» показано, что молекула ДНК составлена из взаимоотношений двойственности додекаэдров и икосаэдров.

Американский математик Д.Винтер утверждает, что строение живого вещества, а точнее структура ДНК генетического кода жизни – представляет собой четырехмерную развертку (по оси времени) вращающегося додекаэдра.

Правильные многогранники

и минералы

Шеелит или ангидрид соляной кислоты (пирамида)

Алмаз (октаэдр)

Кристаллы пирита или сернистого колчедана FeS (додекаэдр)

Хрусталь (призма)

Поваренная соль (куб)

Кристаллы куприта (октаэдр)

Природные минералы бывают разных цветов, обычно прозрачные, и что самое главное, обладают красивой правильной формой. Чаще всего кристаллы минералов представляют собой правильные многогранники, грани их идеально плоские, ребра строго прямые. Известный ученый Шафрановский пишет: «В ограненном кристалле само природное явление, как бы ставит готовую задачу, решение которой невозможно без углубленных математических изысканий».

Создания природы красивы и симметричны. В кристаллографии существует раздел, который называется «геометрическая кристаллография».

Многогранники в ювелирных изделиях

Кулон «Алхимия», серебро. Мощный очиститель энергии. Создает гармоничные частоты, очищая и балансируя. Его можно повесить в большом помещении для очищения и создания гармоничной атмосферы. Этот кулон называется «Алхимия», потому что он символизирует многие молекулярные структуры, а это значит, что он трансформирует разные материалы. Форма кулона – кубооктаэдр. В основе кулона – октаэдр (двойная пирамида).

Хотя и редко, встречаются черырех- и шестилучевые звездчатые гранаты

Кулоны-подвески – многогранники.

Звездчатые многогранники

в природе

Многие формы звездчатых многогранников подсказывает сама природа. Снежинки – это снежный или ледяной кристалл, звездчатый многогранник, чаще всего в форме шести-лучевых звездочек или шестиугольных пластинок. Сейчас известно несколько тысяч различных типов снежинок.

Правильные многогранники для развлечения

Правильные многогранники известны с древнейших времен. Их орнаментные модели можно найти на разных каменных шарах созданных в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.

Правильные многогранники для развлечения

Интересные представители правильных многогранников являются механические головоломки.

Созданные венгерским преподавателем архитектуры Эрнё Рубиком « Кубик Рубика » (гексаэдр), составленный из 26 кубов, и « Пирамидка Мефферта » (тетраэдр), созданная русским инженером А.А.Ордынцовым .

Головоломки-игрушки в виде разных многогранников.

Правильные многогранники для развлечения

Кусудама – модульная оригами, бумажная модель, которая обычно (но не всегда) формируется сшиванием или склеиванием вместе концов множества одинаковых пирамидальных модулей

Пентаграмма – для построения

новых многогранников

Начиная с 7 века до нашей эры в Древней Греции создаются философские школы, в которых происходит постепенный переход от практической к философской геометрии. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства.

Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком пифагорейцев бала пентаграмма, на языке математики – это правильный невыпуклый или звездчатый пятиугольник, с применением которого строились правильные многогранники. В переводе с греческого – пять линий. Пентаграмме присваивалось способность защищать человека от злых духов.

Гипотеза В.Макарова, В.Морозова и Н.Гончарова:

Идеи Пифагора, Платона, Кеплера о связи правильных многогранников с гармоничным устройством мира нашли свое продолжение в интересной научной гипотезе, которую в начале 80-х годов высказали московские инженеры В.Макаров, В.Морозов, Н.Гончаров. Они считают, что ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. Лучи кристалла обуславливают икосаэдро-додекаэрическую структуру Земли. Многие залежи полезных ископаемых тянутся вдоль икосаэдро-додекаэдровой сетки.

В местах пересечения рёбер располагаются очаги древних культур и цивилизаций.

В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана, шотландское озеро Лох-Несс, Бермудский треугольник.

Применение многогранников в архитектуре

Формы многогранников придают зданиям особый вид. Чаще всего это параллелепипеды. Но бывают и другие многогранники – и это не только красивые, но и прочные, надежные и уникальные сооружения.

Великая пирамида в Гизе . Эта Египетская пирамида является древнейшим из Семи чудес древности. Единственное из чудес, сохранившееся до наших дней. Великая пирамида во времена своего создания была самым высоким сооружением. Удерживала этот рекорд почти 4000 лет.

Многогранники Китая

Готический стиль

Александрийский

маяк

Елабужский институт КФУ

Университетская

площадь в Москве

Спасская башня Казанского кремля состоит из четырех ярусов: куб, призмы и пирамида.

Мечеть Кул-Шариф

Башня

Сююмбике

Применение правильных и звездчатых

многогранников в архитектуре

Дворец счастья в Ашхабаде , 11-этажное здание представляет собой трехступенчатое сооружение, каждая сторона которого имеет вид восьмиконечной звезды.

Здание Национальной библиотеки в Минске имеет форму стеклянного ромбокубооктаэдра

Купола Б. Фуллера в современной

архитектуре

Фуллер Ричард Бакминстер (1895-1983), американский архитектор и инженер. Разработал легкие и прочные «геодезические купола».

Идея «геодезических куполов» достаточно проста, сфера представляется в виде многогранника (икосаэдра), то есть двадцатигранника со сторонами в виде правильных треугольников. Эта фигура и разворачивается на плоскость, давая неискаженные соотношения по всей поверхности.

Правильные многогранники будущего

Использованные Интернет-ресурсы:

• http://mirznanii.com/a/315332/pravilnye-mnogogranniki-2
• https :// znanija.com/task/3231925
• http:// dok.opredelim.com/docs/index-4789.html
• http:// otherreferats.allbest.ru/mathematics/00238030_0.html
• http://ppt4web.ru/geometrija/pravilnye-i-polupravilnye-mnogogranniki0.html
• https://yandex.ru/images/search?textD0%BA%D0%B8&stype=image&lr=43&noreask=1&parent-reqid=1483952945892857-344282573591779764322248-sas1-3626&source=wiz