Россия, пгт Серышево
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 20.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 13.02.2024 09:54
Новоселова Галина Валентиновна
Учитель математики
61 год
970
59 292 
Местоположение
Призма и разверток
Категория:
Алгебра
13.12.2023 10:07
Просмотр содержимого документа
«Призма и разверток»
Призма
Понятие призмы
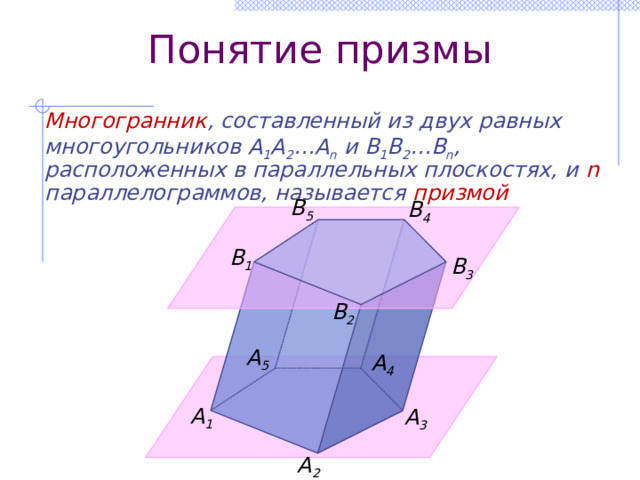
Многогранник , составленный из двух равных многоугольников A 1 A 2 …A n и B 1 B 2 …B n , расположенных в параллельных плоскостях, и n параллелограммов, называется призмой
В 5
В 4
В 1
В 3
В 2
A 5
A 4
A 1
A 3
A 2
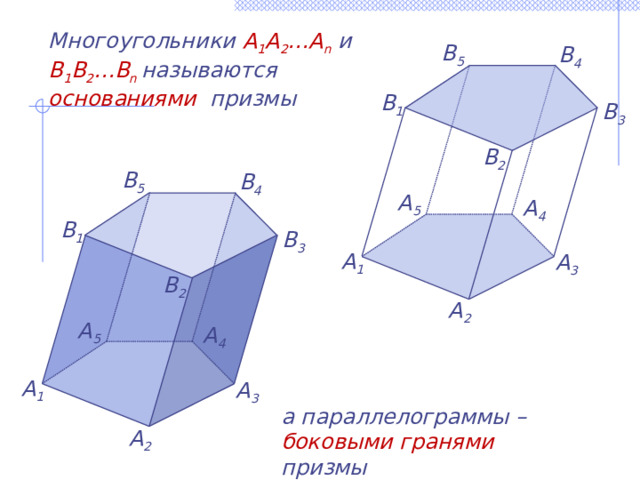
Многоугольники A 1 A 2 …A n и B 1 B 2 …B n называются основаниями призмы
В 5
В 4
В 1
В 3
В 2
В 5
В 4
A 5
A 4
В 1
В 3
A 1
A 3
В 2
A 2
A 5
A 4
A 1
A 3
а параллелограммы – боковыми гранями призмы
A 2
В 5
В 4
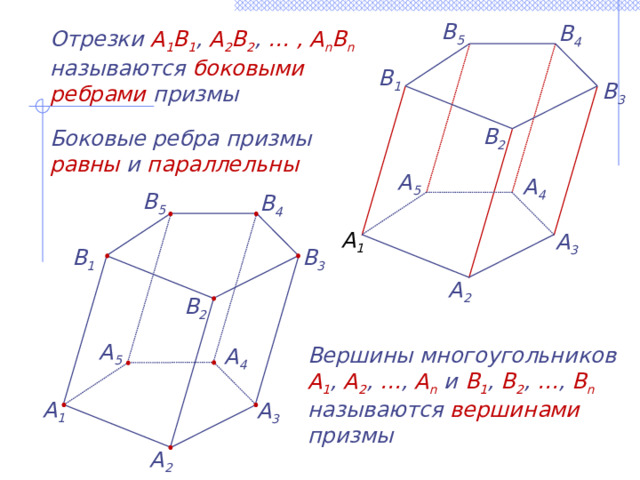
Отрезки A 1 B 1 , A 2 B 2 , … , A n B n называются боковыми ребрами призмы
В 1
В 3
В 2
Боковые ребра призмы равны и параллельны
A 5
A 4
В 5
В 4
A 1
A 3
В 1
В 3
A 2
В 2
A 5
Вершины многоугольников A 1 , A 2 , … , A n и B 1 , B 2 , … , B n называются вершинами призмы
A 4
A 1
A 3
A 2
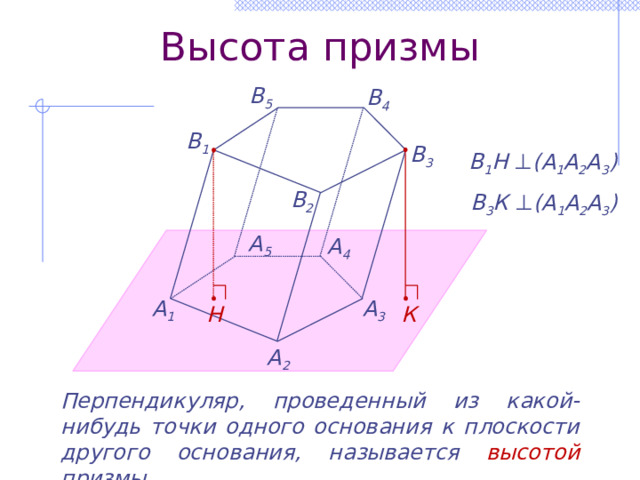
Высота призмы
В 5
В 4
В 1
В 3
В 1 Н ⊥ (А 1 А 2 А 3 )
В 2
В 3 К ⊥ (А 1 А 2 А 3 )
A 5
A 4
A 3
A 1
К
Н
A 2
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы
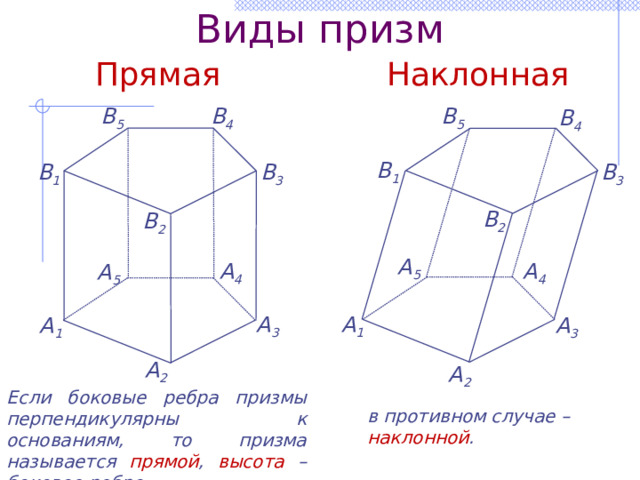
Виды призм
Прямая
Наклонная
В 4
В 5
В 5
В 4
В 1
В 3
В 3
В 1
В 2
В 2
A 5
A 4
A 4
A 5
A 1
A 3
A 1
A 3
A 2
A 2
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой , высота – боковое ребро
в противном случае – наклонной .
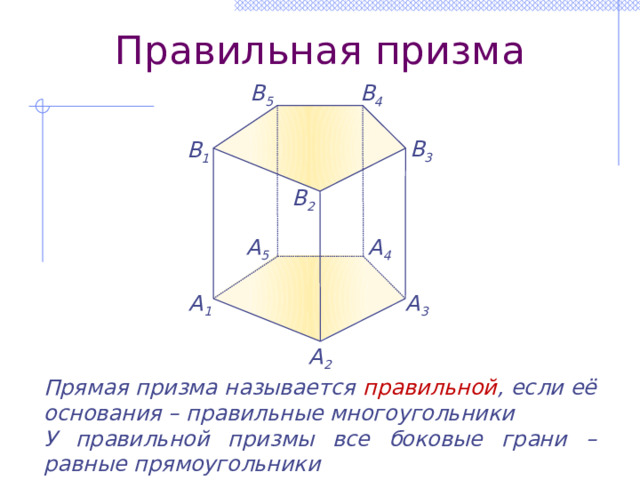
Правильная призма
В 4
В 5
В 3
В 1
В 2
A 5
A 4
A 3
A 1
A 2
Прямая призма называется правильной , если её основания – правильные многоугольники
У правильной призмы все боковые грани – равные прямоугольники
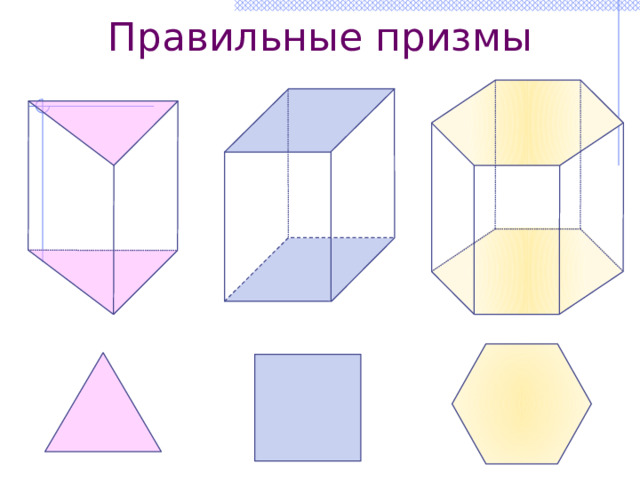
Правильные призмы
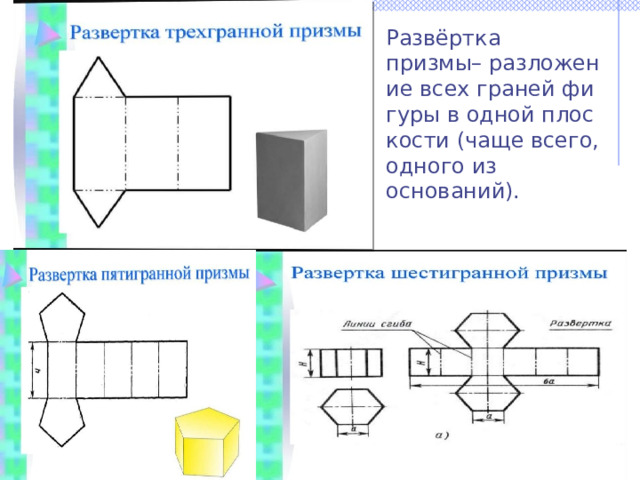
Развёртка призмы– разложение всех граней фигуры в одной плоскости (чаще всего, одного из оснований).
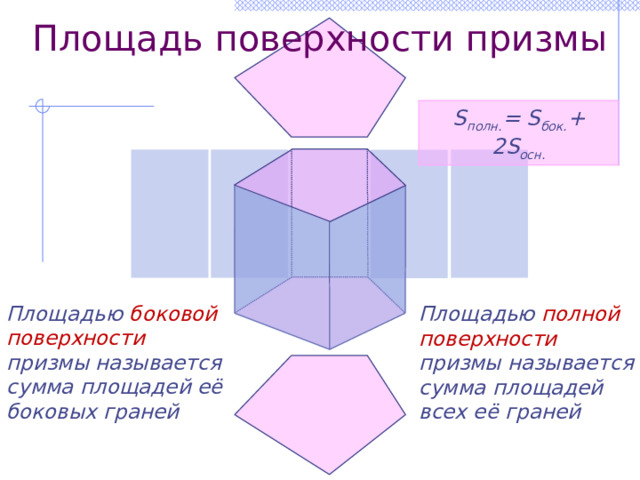
Площадь поверхности призмы
S полн. = S бок. + 2S осн.
Площадью боковой поверхности призмы называется сумма площадей её боковых граней
Площадью полной поверхности призмы называется сумма площадей всех её граней
Теорема о площади боковой поверхности прямой призмы
Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы
S бок. = Р осн. · h
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
