Муниципальное бюджетное общеобразовательное учреждение
Лежневская средняя школа №11
(МБОУ Лежневская СШ №11)
Адрес: 155120, Россия, Ивановская область, п. Лежнево, ул.Островского, д.17
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
Исследование свойств ленты Мёбиуса
Выполнен учеником
5а класса МБОУ Лежневской СШ №11 Гусевым Никитой
Руководитель
учитель математики
Смирнова Светлана Николаевна
п.Лежнево
2022г.
Введение.
Математика наука сложная и серьезная, но в ней встречаются интересные объекты, которые могут показаться занимательными и удивительными. С одним из таких объектов – лентой Мёбиуса я решил познакомиться поближе. Удивительные свойства листа Мёбиуса использовались и используются в кулинарии, в технике, в физике, в живописи, в архитектуре, в оформлении ювелирных изделий и бижутерии. Наконец, этот математический объект позволяет при помощи несложных манипуляций выполнить самые настоящие фокусы.
Цель.
Исследовать свойства ленты Мёбиуса.
Задачи:
Поиск и изучение информации о ленте Мёбиуса:
- что из себя представляет;
- история открытия;
- какие виды бывают;
- свойства;
- применение в технике, искусстве, архитектуре.
2. Проведение серии опытов с лентой Мёбиуса;
3. Фиксация опытов в таблице и на видеофайлах;
4. Подготовка отчета-презентации.
Предмет исследования: лента Мёбиуса.
Объект исследования: свойства ленты Мёбиуса, позволяющие проводить занимательные опыты.
Методы работы над проектом:
Изучение литературы и иной информации по теме;
Моделирование односкрутных и многоскрутных лент Мёбиуса для проведения серии опытов;
Постановка и описание опытов, их видеофиксация.
План работы над проектом: Исследование выполняется поэтапно в соответствии с поставленными задачами.
|
| Этап работы | Время выполнения | Помощники |
| 1 | Поиск и изучение информации о ленте Мёбиуса | 1-13 марта | Интернет |
| 2 | Проведение серии опытов с лентой Мёбиуса и их фиксация на фото | 14-22 марта | Родители, руководитель проекта |
| 3 | Фиксация результатов опытов в таблице | до 31.03.22 | руководитель проекта |
| 4 | Подготовка отчета-презентации | до 7.04.22 | Руководитель проекта |
| 5 | Оформление проекта | До 15.04.22 | Родители, руководитель проекта |
2. Ход работы.
1. Основное содержание.
1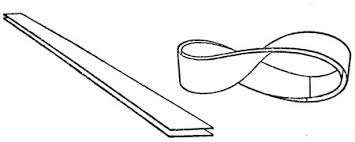 .1 Лента Мебиуса (или ее еще называют петля Мебиуса, лист Мебиуса и даже кольцо Мебиуса) – одна из наиболее известных в математике поверхностей. Это лента достаточной длины, концы которой нужно склеить, предварительно перевернув один конец. Изучением свойств ленты Мёбиуса занимается топология.1
.1 Лента Мебиуса (или ее еще называют петля Мебиуса, лист Мебиуса и даже кольцо Мебиуса) – одна из наиболее известных в математике поверхностей. Это лента достаточной длины, концы которой нужно склеить, предварительно перевернув один конец. Изучением свойств ленты Мёбиуса занимается топология.1
1.2 История открытия.
Считается, что лента Мёбиуса была открыта независимо друг от друга двумя немецкими математиками А.Ф. Мёбиусом (имя которого и получила лента) и И.Б. Листингом (ему повезло меньше) в 1858 году, хотя на самом деле похожий объект был изображен древними римлянами еще в III веке нашей эры.
Н емецкий геометр и астроном Август Фердинанд Мёбиус (17.11.1790 – 26.09.1868), профессор Лейпцигского университета, был учеником «короля математиков» Гаусса. Мёбиус стал одним из крупнейших геометров XIX века. В возрасте 68 лет ему удалось сделать открытие поразительной красоты. Идея пришла ему в голову, когда служанка неправильно сшила ленту.
емецкий геометр и астроном Август Фердинанд Мёбиус (17.11.1790 – 26.09.1868), профессор Лейпцигского университета, был учеником «короля математиков» Гаусса. Мёбиус стал одним из крупнейших геометров XIX века. В возрасте 68 лет ему удалось сделать открытие поразительной красоты. Идея пришла ему в голову, когда служанка неправильно сшила ленту.
1.3 Свойства ленты Мебиуса.
Односторонность. У листа Мёбиуса – всего одна сторона.
Непрерывность. На листе Мёбиуса любая точка может быть соединена с любой другой точкой и при этом ни разу не придётся переползать через край “ленты”. Если на внутреннюю сторону простого кольца посадить паука, а на внутреннюю сторону муху и разрешить им ползать как угодно, запретив лишь переползать через края кольца, то паук не сможет добраться до мухи. А если их обоих посадить на лист Мёбиуса, то бедная муха будет съедена, если, конечно, паук бегает быстрее!
Связность. Лист Мёбиуса двусвязен, т.к. если разрезать его вдоль, он превратится не в два отдельных кольца, а в одну целую ленту.
1.4 Примеры применения в технике, искусстве, архитектуре, быту.

 Лента Мёбиуса в искусстве.
Лента Мёбиуса в искусстве.
Л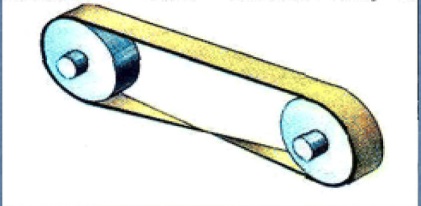 ист Мёбиуса служил вдохновением для скульптур и для графического искусства. Эшер был одним из художников, кто особенно любил его и посвятил несколько своих литографий этому математическому объекту. Одна из известных показывает муравьев, ползающих по поверхности листа Мёбиуса.
ист Мёбиуса служил вдохновением для скульптур и для графического искусства. Эшер был одним из художников, кто особенно любил его и посвятил несколько своих литографий этому математическому объекту. Одна из известных показывает муравьев, ползающих по поверхности листа Мёбиуса.
Лента Мёбиуса в технике.
Полоса ленточного конвейера, шлифовальная лента, выполненная в виде ленты Мёбиуса, изнашивается вдвое меньше, потому что вся поверхность ленты изнашивается равномерно.
Также в системах записи на непрерывную плёнку применялись ленты Мёбиуса (чтобы увеличить время записи).
В матрицах принтера красящая лента имела вид листа Мёбиуса для увеличения срока годности.
Лента Мёбиуса в архитектуре.


Ювелиры посвящают свои работы ленте Мёбиуса.



Примеры предметов быта в форме ленты Мёбиуса


М
 еждународный символ переработки представляет из себя лист Мёбиуса.
еждународный символ переработки представляет из себя лист Мёбиуса.
Он так же красуется на эмблеме механико-математического факультета МГУ.
Проведение и фиксация опытов с лентой Мёбиуса.
| № опыта | Опыт | Результат | Примечания |
| 1. | Два склеенных листа Мёбиуса разрезал каждое посередине | Получил два сцепленных друг с другом сердечка. | Фотоотчет Приложение 1 |
| 2. | Лист Мёбиуса разрезал по середине вдоль. | Получил 1 кольцо, длина которого в два раза больше, ширина в два раза уже, перекручено на 1 полный оборот. | Фотоотчет Приложение 2 |
| 3. | Лист Мёбиуса разрезал вдоль на расстоянии 1/3 от края. | Получил два сцепленных друг с другом кольца: одно большое, одно маленькое | Фотоотчет Приложение 2 |
| 4. | Двухскрутный лист Мёбиуса разрезал вдоль посередине | Получил два сцепленных друг с другом одинаковых кольца. | Фотоотчет Приложение 3 |
| 5. | Трехскрутный лист Мёбиуса разрезал вдоль посередине | Получил кольцо с узелком. Узел можно переместить вдоль кольца, но избавиться от него нельзя. | Фотоотчет Приложение 3 |
| 6. | На односкрутном листе Мёбиуса провел непрерывную линию. | Линия замкнулась в той точке, в которой начиналась. При этом она прошла и снаружи и внутри кольца. У ленты Мёбиуса оказалась одна поверхность.
| Фотоотчет Приложение 4 |
Заключение:
В результате работы я познакомился с интересным математическим объектом – лентой Мёбиуса, изучил её необыкновенные свойства, зная которые можно, например, подготовить и продемонстрировать интересные, простые, но зрелищные фокусы. Я рад поделиться своими открытиями с каждым. Теперь и вы при желании можете почувствовать себя немного волшебниками.
3. Источники информации
https://ru.wikipedia.org/wiki/%D0%9B%D0%B5%D0%BD%D1%82%D0%B0_%D0%9C%D1%91%D0%B1%D0%B8%D1%83%D1%81%D0%B0
https://to-name.ru/biography/avgust-mjobius.htm
https://kozelrozel.jimdofree.com/%D1%83%D0%B4%D0%B8%D0%B2%D0%B8%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5-%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5-%D0%B3%D0%BE%D0%BB%D0%BE%D0%B2%D0%BE%D0%BB%D0%BE%D0%BC%D0%BA%D0%B8/%D0%BB%D0%B8%D1%81%D1%82-%D0%BC%D0%B5%D0%B1%D0%B8%D1%83%D1%81%D0%B0/%D0%BB%D0%B8%D1%81%D1%82-%D0%BC%D1%91%D0%B1%D0%B8%D1%83%D1%81%D0%B0-%D0%B2-%D0%B8%D1%81%D0%BA%D1%83%D1%81%D1%81%D1%82%D0%B2%D0%B5-%D0%B8-%D0%B0%D1%80%D1%85%D0%B8%D1%82%D0%B5%D0%BA%D1%82%D1%83%D1%80%D0%B5/
https://www.google.com/search?rlz=1C1GIVA_enRU969RU969&sxsrf=APq-WButKtA3kVbRUfDesmgTE75PbQuMPA:1650298858166&source=univ&tbm=isch&q=%D0%BB%D0%B8%D1%81%D1%82+%D0%BC%D0%B5%D0%B1%D0%B8%D1%83%D1%81%D0%B0+%D0%B2+%D1%8E%D0%B2%D0%B5%D0%BB%D0%B8%D1%80%D0%BD%D0%BE%D0%BC+%D0%B4%D0%B5%D0%BB%D0%B5&fir=WwThsYekqW2VfM%252CPnMPoeI7JgD06M%252C_%253BDujg1zWxK_PxfM%252CPnMPoeI7JgD06M%252C_%253BftBdnNFOqkRZRM%252CUU_lKcvKd8IJbM%252C_%253BMGkp2yXWMz8OWM%252CUU_lKcvKd8IJbM%252C_%253B_f9SNnL1P3_jQM%252CUU_lKcvKd8IJbM%252C_%253B8FGgCcigHgGH-M%252CUU_lKcvKd8IJbM%252C_%253BLTqA_QE4QKLtXM%252Cs_WF2alfU3bNBM%252C_%253BmBJ1NWoMC1WNfM%252Ciu0AuNWbtwzpwM%252C_%253BTs-eOnJQhBcnsM%252CUU_lKcvKd8IJbM%252C_%253BkIqn-5XQMICTIM%252CNcKm8SHkClG5hM%252C_&usg=AI4_-kS8jANvIvC69jthDnQtjnTPaMEnOA&sa=X&ved=2ahUKEwi4_tqpgp73AhVL-yoKHZBiCnEQjJkEegQIGBAC&biw=1920&bih=969&dpr=1
Приложение 1
Опыт со склеенными кольцами.












При разрезании посередине второй пары колец получил два переплетенных сердечка, каждое из которых оказалось односкрутной лентой Мёбиуса.
Заготовил пары колец (обыкновенных и односкрутных лент Мёбиуса).
Склеил их под прямым углом.
Разрезал кольца посередине.
Результат опыта с простыми кольцами – рамка.

Приложение 2
Опыт с односкрутной лентой Мёбиуса №1.




Заготовил односкрутную ленту Мёбиуса.
Разрезал ее посередине.
Результат опыта – одно большое кольцо.
Опыт с односкрутной лентой Мёбиуса №2.






Результат опыта: два переплетенных кольца. Одно кольцо (тонкое) получилось большим, второе кольцо по размерам как было исходное.
Заготовил односкрутную ленту Мёбиуса.
Разрезал ее посередине на расстоянии 1 см от кромки.
Приложение 3
Опыт с двухскрутной лентой Мёбиуса.




Заготовил двухскрутную ленту Мёбиуса.
Разрезал ее посередине.
Результат опыта – два одинаковых переплетенных кольца.
Опыт с трехскрутной лентой Мёбиуса.





Результат опыта: кольцо с узелком. Узел можно переместить вдоль кольца, но избавиться от него нельзя.
Заготовил трехскрутную ленту Мёбиуса.
Разрезал ее посередине.
Приложение 4
Опыт с лентой Мёбиуса.






Результат опыта: линия замкнулась в той точке, в которой начиналась. При этом она прошла и снаружи и внутри кольца. У ленты Мёбиуса оказалась одна поверхность.
Заготовил ленту Мёбиуса.
Нарисовал точку и от этой точки начал рисовать непрерывную линию посередине кольца.
1� Топология – раздел математики, изучающий в самом общем виде явления непрерывности (Википедия).
11







 .1 Лента Мебиуса (или ее еще называют петля Мебиуса, лист Мебиуса и даже кольцо Мебиуса) – одна из наиболее известных в математике поверхностей. Это лента достаточной длины, концы которой нужно склеить, предварительно перевернув один конец. Изучением свойств ленты Мёбиуса занимается топология.1
.1 Лента Мебиуса (или ее еще называют петля Мебиуса, лист Мебиуса и даже кольцо Мебиуса) – одна из наиболее известных в математике поверхностей. Это лента достаточной длины, концы которой нужно склеить, предварительно перевернув один конец. Изучением свойств ленты Мёбиуса занимается топология.1 емецкий геометр и астроном Август Фердинанд Мёбиус (17.11.1790 – 26.09.1868), профессор Лейпцигского университета, был учеником «короля математиков» Гаусса. Мёбиус стал одним из крупнейших геометров XIX века. В возрасте 68 лет ему удалось сделать открытие поразительной красоты. Идея пришла ему в голову, когда служанка неправильно сшила ленту.
емецкий геометр и астроном Август Фердинанд Мёбиус (17.11.1790 – 26.09.1868), профессор Лейпцигского университета, был учеником «короля математиков» Гаусса. Мёбиус стал одним из крупнейших геометров XIX века. В возрасте 68 лет ему удалось сделать открытие поразительной красоты. Идея пришла ему в голову, когда служанка неправильно сшила ленту.
 Лента Мёбиуса в искусстве.
Лента Мёбиуса в искусстве. ист Мёбиуса служил вдохновением для скульптур и для графического искусства. Эшер был одним из художников, кто особенно любил его и посвятил несколько своих литографий этому математическому объекту. Одна из известных показывает муравьев, ползающих по поверхности листа Мёбиуса.
ист Мёбиуса служил вдохновением для скульптур и для графического искусства. Эшер был одним из художников, кто особенно любил его и посвятил несколько своих литографий этому математическому объекту. Одна из известных показывает муравьев, ползающих по поверхности листа Мёбиуса.







 еждународный символ переработки представляет из себя лист Мёбиуса.
еждународный символ переработки представляет из себя лист Мёбиуса. 













































