Проект на тему: «Методы решения симметрических и однородных систем рациональных уравнений».
Автор: Хабибова Патимат Магомедовна – учитель математики МКОУ «Ободинская СОШ»
ПЛАН.
Введение.
Раздел I.
Знакомство с темой проекта. Поиск информации и справочной литературы в библиотеке и сети Интернет. Анализ и обработка информации. Обсуждение возможных вариантов исследования, сравнение предполагаемых стратегий, выбор способов, сбор и изучение информации, составление плана работы над проектом.
Основные теоретические положения.
Методы решения систем линейных однородных уравнений.
Методы решения систем нелинейных однородных уравнений. а) Однородные системы уравнений;
б) Симметричные системы уравнений.
Раздел.
Опыт работы.
Заключение.
Информационные источники.
Приложения.
Введение.
Цель данного проекта – глубоко изучить литературу по проблеме, с научных позиций осмыслить, обобщить, проанализировать педагогический опыт и определить пути в данном направлении. Расширить свои знания в области математики, связанные с понятием «Системы уравнений». На эти темы отдельных часов в программе не выделено, она изучается в рамках тех уроков, где рассматриваются конкретные виды уравнений: целые, дробно-рациональные, иррациональные, показательные, логарифмические, тригонометрические. Задача проекта заключается в том, что для успешной подготовки учащихся к сдаче ЕГЭ требуется умение решать различные системы уравнений, а в курсе средней школы им отведено недостаточно времени, необходимого познать этот вопрос глубже. Основная часть проекта состоит из трёх частей: основные теоретические положения темы, методы решения однородных и симметрических уравнений,опыт работы ( методы решения однородных и симметрических систем уравнений).
РАЗДЕЛ 1. 1.1 Основные теоретические положения.
Если система однородных линейных уравнений:

имеет:
 , то она имеет единственное решение
, то она имеет единственное решение 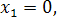
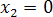 ,
,  ;
;
 , то она имеет ненулевые решения.
, то она имеет ненулевые решения.
Теорема. Для того чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг  ее основной матрицы был меньше числа
ее основной матрицы был меньше числа  неизвестных, т.е.
неизвестных, т.е. 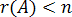 .
.
1.2 Методы решения систем линейных однородных уравнений. Метод Крамера. Пример. Решить систему 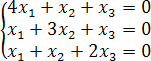 .
.
Решение.
 система имеет только нулевое решение
система имеет только нулевое решение  .
.
Ответ: 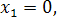
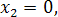
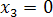 .
.
Пример. Решить систему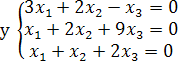 .
.
Решение.
 матрица системы.
матрица системы.
Так как определитель системы 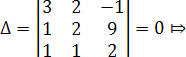 система имеет отличные от нуля решения.
система имеет отличные от нуля решения.
Найдем ранг матрицы 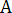 . Поскольку определитель третьего порядка равен нулю, рассмотрим определитель второго порядка
. Поскольку определитель третьего порядка равен нулю, рассмотрим определитель второго порядка
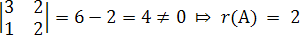 .
.
Этот определитель является базисным.
Так как 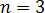 и
и 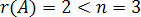 , то система имеет бесчисленное множество решений.
, то система имеет бесчисленное множество решений.
Найдем их.
1. Составим систему из уравнений коэффициенты, которых вошли в базисный минор: 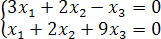 .
.
Неизвестные  – главные неизвестные, неизвестное
– главные неизвестные, неизвестное 
Решаем систему методом Крамера.
Определитель системы  , найдем дополнительные определители:
, найдем дополнительные определители:
,
,
Итак, ; общее решение.
2. Положив  получаем одно частное решение:
получаем одно частное решение:
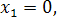
 .
.
Положив  получаем второе частное решение:
получаем второе частное решение:


 .
.
Положив  получаем третье частное решение:
получаем третье частное решение:


 .
.
Ответ:  ;
;  .
.
Метод Гаусса.
1. Решить систему уравнений
Решение. Выполним элементарные преобразования над строками матрицы коэффициентов, приведя ее к ступенчатому виду:
Ранг матрицы равен 3, тогда как число неизвестных равно 4. Поэтому одну из неизвестных, например,  следует рассматривать как свободный параметр.
следует рассматривать как свободный параметр.
Далее нужно присвоить этому параметру произвольное значение  и выразить базисные неизвестные
и выразить базисные неизвестные  ,
,  и
и  через c.
через c.
Преобразованная матрица соответствует следующей системе уравнений:
Из последнего уравнения следует, что  .
.
Выразим остальные базисные переменные:


Таким образом, общее решение системы найдено
1.2 МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.
В этой части проекта я рассмотрю два основных метода решения систем нелинейных уравнений:
1) Однородные системы нелинейных уравнений;
2) Симметричные системы уравнений.
1) Однородные системы уравнений:
Уравнения называются однородными, если все слагаемые, содержащие неизвестные, имеют одну и ту же степень (показатели степеней разных неизвестных в слагаемых складываются). ИЛИ: Определение . Система двух уравнений с двумя неизвестными вида
называется однородной. Многочлены в левых частях уравнений системы являются однородными многочленами степени  .
.
Пример Решить систему уравнений 
Решение. Положим  , тогда из первого уравнения системы находим
, тогда из первого уравнения системы находим  . Но пара чисел
. Но пара чисел  не является решением второго уравнения системы. Поэтому рассмотрим случай, когда
не является решением второго уравнения системы. Поэтому рассмотрим случай, когда  . Разделим обе части первого уравнения на
. Разделим обе части первого уравнения на  . Получим
. Получим  . Это уравнение вместе со вторым уравнением данной системы образует систему, равносильную исходной. Решая данное уравнение, имеем
. Это уравнение вместе со вторым уравнением данной системы образует систему, равносильную исходной. Решая данное уравнение, имеем  или
или  , т.е.
, т.е.  или
или  . Тогда данная система равносильна совокупности двух систем:
. Тогда данная система равносильна совокупности двух систем:  и
и 
Первая система этой совокупности не имеет действительных решений. Решив вторую систему совокупности, получим  , тогда
, тогда  .
.
Ответ.  ;
;  .
.
В примере рассмотрели однородную систему, в которой одно из чисел  ,
,  равно
равно  . Если в однородной системе
. Если в однородной системе  ,
,  , то надо такую систему свести к виду предыдущей (т.е. одно из чисел
, то надо такую систему свести к виду предыдущей (т.е. одно из чисел  ,
,  равно
равно  ). Покажем это на примере.
). Покажем это на примере.
Пример . Решить систему уравнений 
Решение. Умножим первое уравнение системы на  , а второе – на
, а второе – на  и сложим полученные уравнения. В результате имеем уравнение
и сложим полученные уравнения. В результате имеем уравнение  , которое вместе с первым уравнением системы образует систему, равносильную исходной. Пара чисел
, которое вместе с первым уравнением системы образует систему, равносильную исходной. Пара чисел  не является решением данной системы, значит можно перейти от последнего уравнения к следующему:
не является решением данной системы, значит можно перейти от последнего уравнения к следующему:  . Решив его, получим
. Решив его, получим  или
или  , т.е.
, т.е.  или
или  . Имеем совокупность двух систем:
. Имеем совокупность двух систем:  и
и  Из первой системы получаем
Из первой системы получаем  ,
,  . Вторая система имеет решения
. Вторая система имеет решения  ,
,  .
.
Ответ.  ;
;  ;
;  ;
;  . Пример Решить систему уравнений
. Пример Решить систему уравнений 
Решение. Первое уравнение системы однородно, но заметим, что все члены его левой части делятся на  . Поэтому данную систему заменим равносильной ей совокупностью двух систем уравнений
. Поэтому данную систему заменим равносильной ей совокупностью двух систем уравнений  и
и  Решая первую систему совокупности, находим
Решая первую систему совокупности, находим  ,
,  ;
;  ,
,  . Процесс решения второй системы известен, ей удовлетворяют четыре пары чисел:
. Процесс решения второй системы известен, ей удовлетворяют четыре пары чисел:


 Ответ.
Ответ.  ;
;  ;
;  ;
;  ;
;  ;
;  .
.
Пример . Решить систему уравнений 
Решение. Пара  удовлетворяет системе. Пусть
удовлетворяет системе. Пусть  . Разделим на
. Разделим на  оба уравнения системы, получим откуда находим
оба уравнения системы, получим откуда находим  Значит,
Значит,  . Положим
. Положим  , тогда
, тогда  . Заметим, что при
. Заметим, что при  имеем
имеем  и
и  . Решения данной системы запишем парой вида
. Решения данной системы запишем парой вида  , где
, где  .
.
Ответ.  ,
,  .
.
Рассмотрим примеры систем, в которых левые части уравнений являются однородными многочленами степени выше второй.
Пример . Решить систему уравнений 
Решение. Разложим левые части уравнений на множители  Разделим уравнения последней системы почленно, в результате получим уравнение
Разделим уравнения последней системы почленно, в результате получим уравнение  . Полученное уравнение вместе с первым уравнением данной системы образует систему, равносильную исходной. Положим
. Полученное уравнение вместе с первым уравнением данной системы образует систему, равносильную исходной. Положим  , получим
, получим  , откуда
, откуда  ,
,  , т.е.
, т.е.  ,
,  . Если
. Если  , то из первого уравнения системы находим
, то из первого уравнения системы находим  и поэтому
и поэтому  . Аналогично, если
. Аналогично, если  , то
, то  ,
,  .
.
Ответ.  ;
;  .
.
Замечание. Систему уравнений в примере можно было решить, используя прием: первое уравнение системы помножить на  , второе – на
, второе – на  и сложить. Получим уравнение
и сложить. Получим уравнение  , далее обе части уравнения можно разделить на
, далее обе части уравнения можно разделить на  . Уравнение, полученное в результате таких преобразований, и первое уравнение данной системы образуют систему, равносильную исходной. Затем решаем кубическое уравнение относительно
. Уравнение, полученное в результате таких преобразований, и первое уравнение данной системы образуют систему, равносильную исходной. Затем решаем кубическое уравнение относительно  . Однако приведенное выше решение примера, через разложение левых частей уравнений на множители и равносильных преобразований с этими уравнениями, привело к решению квадратного уравнения, решить которое проще кубического.
. Однако приведенное выше решение примера, через разложение левых частей уравнений на множители и равносильных преобразований с этими уравнениями, привело к решению квадратного уравнения, решить которое проще кубического.
Оказывается, существует стандартная подстановка x = ty (y ≠ 0), которая позволяет решить систему однородных уравнений:
Пример:
Решение.
Пусть x = ty (y ≠ 0), тогда
Зная t, легко сразу найти  , учитывая, что . Используя это, найдём y,а затем и х a) t =3
, учитывая, что . Используя это, найдём y,а затем и х a) t =3 
b) t = 

При y = 0 решения нет.
Ответ: {(3√3; √3); (-3√3; √3); (4; 5); (-4; -5)}.
Пример 3
Решить систему уравнений:
Решение
| Ни одно из уравнений системы не является однородным, однако в левой части уравнений стоят однородные функции. Применим стандартный приём, который позволяет свести систему такого вида к однородному уравнению. Умножим первое уравнение на 4, а второе на 3 и вычтем из первого уравнения второе. Имеем: А это уравнение уже однородное. Очевидно, что пара (0; 0) является его решением, однако непосредственной подстановкой можно убедиться, что эта пара не является решением исходной системы уравнений. Значит, разделим уравнение на  Получим: Получим: Стандартная замена  приводит нас к квадратному уравнению приводит нас к квадратному уравнению  корни которого корни которого  и и  Система распалась на две: 1) Система распалась на две: 1) 2) Ответ.  
|
|
|
Симметрические системы.
| Теорема 1. (о симметрических многочленах) Любой симметрический многочлен от двух переменных представим в виде функции от двух основных симметрических многочленов
|
Другими словами, для любого симметрического многочлена f (x, y) существует такая функция двух переменных φ (u, v), что
Доказательство этого факта хотя и доступно школьнику, но далеко выходит за рамки школьного курса, поэтому мы приведём лишь примеры, которые иллюстрируют применение этой теоремы.
Пример 3
Функция  может быть преобразована следующим образом:
может быть преобразована следующим образом:
где 
Пример 4
Функция  может быть преобразована следующим образом:
может быть преобразована следующим образом:
где 
Аналогично, симметрическая функция трёх переменных определяется как функция, которая не изменяет своего значения при произвольных перестановках своих аргументов, то есть
Для симметрических многочленов трёх переменных справедлива точно такая же теорема, как и для многочленов двух переменных, а именно:
| Теорема 2. (о симметрических многочленах) Любой симметрический многочлен от трёх переменных представим в виде функции от трёх основных симметрических многочленов:
|
Другими словами, для любого симметрического многочлена f (x, y) существует такая функция трёх переменных θ (u, v, w), что
Применим эту теорему для упрощения систем уравнений.
Пример 5
Решите систему уравнений
Решение
| Эта система является симметрической, поэтому делаем стандартную замену   Поскольку Поскольку  а из второго уравнения системы следует, что а из второго уравнения системы следует, что  то то  Левая часть второго уравнения перепишется так: Левая часть второго уравнения перепишется так:  Относительно u и v получаем систему Относительно u и v получаем систему Перейдем к переменным x и y: 1) 2) Ответ.  |
Пример 6
Решите систему уравнений
Решение
| Эта система – симметрическая, поэтому делаем стандартную замену u = x + y, v = xy. Преобразуем левую часть первого уравнения: тогда система принимает вид: Итак, для u получаем уравнение  Вспомним теорему о рациональных корнях многочленов. Рациональные корни нашего уравнения нужно искать среди делителей числа –4. Перебирая все делители, убеждаемся, что рациональных корней у уравнения нет. Однако эта теорема и не была теоремой существования корней. Указанная теорема констатировала лишь следующее: если у многочлена с целыми коэффициентами существуют рациональные корни (но для них имеется ещё возможность НЕ существовать), то эти корни будут иметь некоторый специальный вид. Тот случай, когда рациональных корней нет, эта теорема и не описывала. Вспомним теорему о рациональных корнях многочленов. Рациональные корни нашего уравнения нужно искать среди делителей числа –4. Перебирая все делители, убеждаемся, что рациональных корней у уравнения нет. Однако эта теорема и не была теоремой существования корней. Указанная теорема констатировала лишь следующее: если у многочлена с целыми коэффициентами существуют рациональные корни (но для них имеется ещё возможность НЕ существовать), то эти корни будут иметь некоторый специальный вид. Тот случай, когда рациональных корней нет, эта теорема и не описывала. Попробуем найти корни уравнения исходной системы среди иррациональных чисел. Однако для этого придется проявить некоторую изобретательность: стандартная замена для симметрических систем здесь, очевидно не работает. Возводя второе уравнение в куб, получим:  Таким образом, по теореме Виета, Таким образом, по теореме Виета,  и и  являются корнями квадратного уравнения являются корнями квадратного уравнения  Отсюда Отсюда  и и  Значит, Значит, Заметим, что мы нашли один из корней уравнения  Ответ. 2) Системы симметричных уравнений:
Пусть  , тогда система имеет вид: , тогда система имеет вид:  . .
Вычтем из первого уравнения второе уравнение:
 
a)  
По теореме, обратной теореме Виета, данная система порождает квадратное уравнение  + 4m + 3 = 0, корнями которого являются x и y. В силу симметричности имеем: (1; 3); (3; 1). + 4m + 3 = 0, корнями которого являются x и y. В силу симметричности имеем: (1; 3); (3; 1).
b)  
Из порождённого квадратного уравнения  - 4n + 3 = 0 следует решения (-3; -1); (-1; -3). - 4n + 3 = 0 следует решения (-3; -1); (-1; -3).
Ответ: {(1; 3); (3; 1); (-3; -1); (-1; -3)}. Пример Решить систему уравнений  Решение. Выполним алгебраическое сложение уравнений системы, предварительно помножив первое уравнение на  , а второе – на , а второе – на  . Получим уравнение, которое со вторым уравнением системы образуют систему, равносильную исходной: Как и в предыдущих примерах, первое уравнение системы можно разделить на . Получим уравнение, которое со вторым уравнением системы образуют систему, равносильную исходной: Как и в предыдущих примерах, первое уравнение системы можно разделить на  . В результате получим уравнение четвертой степени, решение которого громоздко. Однако, решив его и реализовав план решения системы, описанный в предыдущих примерах, получим ответ. Но дана симметрическая система, а значит, с помощью введения новых неизвестных может быть преобразована к более простому виду. Покажем это. . В результате получим уравнение четвертой степени, решение которого громоздко. Однако, решив его и реализовав план решения системы, описанный в предыдущих примерах, получим ответ. Но дана симметрическая система, а значит, с помощью введения новых неизвестных может быть преобразована к более простому виду. Покажем это.  Пусть Пусть  , ,  , тогда имеем систему , тогда имеем систему  и т.д. Решая исходную систему любым из предложенных способов, получим и т.д. Решая исходную систему любым из предложенных способов, получим  ; ;  ; ;  ; ;  . . Ответ.  ; ;  ; ;  ; ;  . . |
Раздел 2
Из опыта работы.
Элективный курс по математике «Уравнения, неравенства и их системы»
Составила: Хабибова Патимат Магомедовна,
учитель математики первой категории МКОУ «Ободинская СОШ» Хунзахского района РД.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Программа данного элективного курса рассчитана на 27 часов и предназначена для учащихся 11 класса. Элективный курс позволит интересующимся школьникам получить дополнительную подготовку и сдать ЕГЭ по предмету на профильном уровне. В настоящее время практика вступительных экзаменов оторвалась от школы. Нам известно насколько велики «ножницы» между требованиями школьной программы и требованиями, которые предъявляют к поступающему ВУЗ.
Курсы, которые предлагают ВУЗы учащимся, ориентируют их на экзамен лишь в данный ВУЗ. Элективный курс «Уравнения, неравенства и их системы» поможет подготовиться учащимся к поступлению в любое высшее учебное заведение, так как основной целью этого курса является знакомство учащихся с общими методами и приемами решения уравнений, неравенств и их систем.
Задачами данного элективного курса являются:
повышение уровня математического и логического мышления учащихся;
развитие навыков исследовательской деятельности,
подготовка выпускника к сдаче конкурсного экзамена по математике.
Работа элективного курса строится на принципах:
научности;
доступности;
опережающей сложности;
вариативности;
самоконтроля.
Однородное тригонометрическое уравнение – это уравнение двух видов:
a sin x + b cos x = 0 (однородное уравнение первой степени)
либо a sin2 x + b sin x cos x + c cos2 x = 0 (однородное уравнение второй степени).
Алгоритм решения однородного уравнения первой степени a sin x + b cos x = 0:
| 1) разделить обе части уравнения на cos x 2) решить получившееся выражение |
Пример: Решим уравнение 2 sin x – 3 cos x = 0.
Решение.
Разделим обе части уравнения на cos x:
2 sin x 3 cos x 0
———— – ———— = ———
cos x cos x cos x Получаем: 2 tg x – 3 = 0, 2 tg x = 3, tg x = 3/2
x = arctg 3/2 + πn
Алгоритм решения однородного уравнения второй степени a sin2 x + b sin x cos x + c cos2 x = 0.
Условие: в уравнении должно быть выражение вида a sin2 x.
Если его нет, то уравнение решается методом разложения на множители.
| 1) Разделить обе части уравнения на cos2 x 2) Ввести новую переменную z, заменяющую tg x (z = tg x) 3) Решить получившееся уравнение |
Пример: Решить уравнение sin2 x – 3 sin x cos x + 2 cos2 x = 0.
Решение.
Разделим обе части уравнения на cos2 x:
sin2 x 3 sin x cos x 2 cos2 x 0
——— – —————— + ———— = ———
cos2 x cos2 x cos2 x cos2 x
Получаем: tg2 x – 3 tg x + 2 = 0.
Вместо tg x введем новую переменную z и получим квадратное уравнение:
z2 – 3z + 2 = 0. Найдем корни: z1 = 1, z2 = 2. Значит: либо tg x = 1, либо tg x = 2.
Сначала найдем x при tg x = 1: x = arctg 1 + πn,x = π/4 + πn.
Теперь найдем x при tg x = 2: x = arctg 2 + πn.
Ответ: x = π/4 + πn; x = arctg 2 + πn.
Однородные логарифмические уравнения.
Пример.
Решить уравнение log23 (х2 – 3х + 4) – 3log3 (х + 5) log3 (х2 – 3х + 4) – 2log23 (х + 5) = 0
Решение.
Область определения уравнения
{х2 – 3х + 4 0,
{х + 5 0. → х -5.
log3 (х + 5) = 0 при х = -4. Проверкой определяем, что данное значение х не является корнем первоначального уравнения.Следовательно можно разделить обе части уравнения на log2 3 (х+5).
Получим log23 (х2 – 3х + 4) / log23 (х + 5) – 3 log3 (х2 – 3х + 4) / log3 (х + 5) + 2 = 0.
Пусть log3 (х2 – 3х + 4) / log3 (х + 5) = t. Тогда t 2– 3 t + 2 = 0. Корни данного уравнения 1; 2. Возвратившись к первоначальной переменной, получим совокупность двух уравнений
[log3 (х2 – 3х + 4) / log3 (х + 5) = 1
[log3 (х2 – 3х + 4) / log3 (х + 5) = 2. Отсюда
[log3 (х2 – 3х + 4) = log3 (х + 5),
[log3 (х2 – 3х + 4) = 2log3 (х + 5).
Выполнив потенцирование, получим
[х2 – 3х + 4 = х + 5,
[х2 – 3х + 4 = (х + 5)2 ;
[х2 – 4х – 1 = 0,
[-13х = 21.
[х = 2 – √5,
[х = 2 + √5, [х = -21/13. Все корни входят в область определения.
Ответ: ,-21/13; 2 – √5; 2 + √5.
Использование однородности
Определение. Показательные уравнения вида  называются однородными.
называются однородными.
Суть метода: Так как показательная функция не может принимать значение, равное нулю, и обе части уравнения можно делить на одно и то же не равное нулю число, разделим обе части уравнения, например, на  .
.
Пример: 2x = 3x Решение:Разделим обе части уравнения на 
 Ответ: x = 0
Ответ: x = 0
Симметрические уравнения
Уравнение степени n называется симметрическим, если у него равны коэффициенты при xn и при хn-r. Таким образом симметрическое уравнение имеет вид: a0xn + a1xn-1 +…+ anxn-r +…+ a1x + a0 = 0. Симметрические уравнения являются частным видом возвратного уравнения, поэтому симметрические уравнения решаются тем же способом, что и возвратные.Различают симметрические уравнения 3-ого порядка и 4-ого порядка. Некоторые свойства симметрических уравнений:
Симметрическое уравнение нечетной степени имеет корень -1.
В результате деления симметрического уравнения нечетной степени на (х + 1) получается симметрическое уравнение четной степени на единицу меньше. 3. Симметрическое уравнение четной степени 2n подстановкой
y = x +1|x может сводиться,на области действительных чисел, к уравнению степени n и к уравнениям второй степени.
1. Уравнения называются симметрическими уравнениями 3-й степени, если они имеют вид ах3 + bx2 + bх + a = 0.
Пример. х3 + 2x2 + 2х + 1 = 0. Решение.У исходного уравнения обязательно есть корень х = -1, поэтому разделим х3 + 2x2 + 2х + 1 на (х + 1) по схеме Горнера:
| . | 1 | 2 | 2 | 1 |
| -1 | 1 | 2 – 1 = 1 | 2 – 1 = 1 | 1 – 1 = 0 |
х3 + 2x2 + 2х + 1 = (х + 1)(x2 + х + 1) = 0.
Квадратное уравнение x2 + х + 1 = 0 не имеет корней.
Ответ: -1.
Другой способ: Поскольку ах3 + вх2 + вх + а = а (х3 + 1) + вх (х+1) = а (х+ 1) (х2 - х+ 1) + вх (х+ 1) = (х+1) (ах2 + (в - а) х + а), то уравнение (1) равносильно совокупности уравнений
х + 1 = 0 и ах2 + (в - а) х + а = 0, решить которую просто.
Пример 1. Решить уравнение
3х3 + 4х2 + 4х + 3 = 0.
Уравнение является симметрическим уравнением третьей степени. Разложим на множители левую часть уравнения
3х3 + 4х2 + 4х + 3 = 3 (х3 + 1) + 4х (х + 1) = ( х + 1) (3х3 – 3х + 3 + 4х) = ( х+ 1) (3х3 + х + 3).
Уравнение равносильно совокупности уравнений
х + 1 = 0 и 3х3 + х + 3 = 0,
х= - 1 D
Ответ: - 1.
2. Уравнения называются симметрическими уравнениями 4-й степени, если они имеют вид ах4 + bx3 + сх2 + bх + a = 0.
Алгоритм решения подобных уравнений таков:
а) Разделить обе части исходного уравнения на х2. Это действие не приведет к потере корня, ведь х = 0 решением заданного уравнения не является.
б) С помощью группировки привести уравнение к виду:
а(x2 + 1/x2) + b(x + 1/x) + c = 0.
в) Ввести новую неизвестную: t = (x + 1/x).
Проделаем преобразования:t2 = x2 +2 + 1/x2. Если теперь выразить x2 + 1/x2, то t2 – 2 = x2 + 1/x2.
г) Решить в новых переменных полученное квадратное уравнение:
аt2 + bt + c – 2a = 0.
д) Сделать обратную подстановку.
Пример.
6х4 – 5х3 – 38x2 – 5х + 6 = 0.
Решение.
6х2 – 5х – 38 – 5/х + 6/х2 = 0, 6(х2 + 1/х2) – 5(х + 1/х) – 38 = 0.
Вводим t: подстановка (x + 1/x) = t. Замена: (x2 + 1/x2) = t2 – 2, имеем:
6t2 – 5t – 50 = 0, t = -5/2 или t = 10/3. Вернемся к переменной х. После обратной замены решим два полученных уравнения: 1) x + 1/x = -5/2; х2 + 5/2 х +1 = 0;
х = -2 или х = -1/2. 2) x + 1/x = 10/3; х2 – 10/3 х + 1 = 0; х = 3 или х = 1/3. Ответ: -2; -1/2; 1/3; 3.
Способы решения некоторых видов уравнений высших степеней
1. Уравнения, которые имеют вид (х + а)n + (х + b)n = c, решаются подстановкой t = x + (a + b)/2. Этот метод называется методом симметризации.
Примером такого уравнения может быть уравнение вида (х + а)4 + (х + b)4 = c.
Пример.
(х + 3)4 + (х + 1)4 = 272.
Решение.
Делаем подстановку, о которой говорилось выше: t = x + (3 + 1)/2 = х + 2, после упрощения: х = t – 2, (t – 2 + 3)4 + (t – 2 + 1)4 = 272, (t + 1)4 + (t – 1)4 = 272. Убрав скобки с помощью формул, получим:t4 + 4t3 + 6t2 + 4t + 1 + t4 – 4t3 + 6t2 – 4t + 1 = 272, 2t4 + 12t2 – 270 = 0, t4 + 6t2 – 135 = 0, t2 = 9 или t2 = -15. Второе уравнение корней не дает, а вот из первого имеем t = ±3. После обратной замены получим, что х = -5 или х = 1. Ответ: -5; 1.
Для решения подобных уравнений часто оказывается эффективным и метод разложения на множители левой части уравнения.
2. Уравнения вида (х + а)(х + b)(x + c)(x + d) = А, где а + d = c + b.
Методика решения подобных уравнений заключается в частичном раскрытии скобок, а затем введении новой переменной. Пример.(х + 1)(х + 2)(x + 3)(x + 4) = 24. Решение. Вычисляем: 1 + 4 = 2 + 3. Группируем скобки по парам: ((х + 1)(x + 4))((х + 2)(x + 3)) = 24, (х2 + 5х + 4)(х2 + 5х + 6) = 24. Сделав замену х2 + 5х + 4 = t, имеем уравнение t(t + 2) = 24, оно является квадратным: t2 + 2t – 24 = 0, t = -6 или t = 4. После выполнения обратной замены, легко находим корни исходного уравнения. Ответ: -5; 0.
3. Уравнения вида (х + а)(х + b)(x + c)(x + d) = Ах2, где аd = cb.
Метод решения заключается в частичном раскрытии скобок, делении обеих частей на х2 и решении совокупности квадратных уравнений.
Пример.
(х + 12)(х + 2)(x + 3)(x + 8) = 4х2.
Решение.
Перемножив в левой части первые две и последние две скобки получим:
(х2 + 14х + 24)(х2 + 11х + 24) = 4х2. Делим на х2 ≠ 0: (х + 14 + 24/х)(х + 11 + 24/х) = 4. Заменой (х + 24/х) = t приходим к квадратному уравнению: (t + 14)(t + 11) = 4; t2 + 25х + 150 = 0. t = 10 или t = 15. Произведя обратную замену х + 24/х = 10 или х + 24/х = 15, находим корни. Ответ: (-15 ± √129)/2; -4; -6.
4. Решить уравнение (3х + 5)4 + (х + 6)3 = 4х2 + 1.
Решение.
Данное уравнение сразу трудно классифицировать и выбрать метод решения. Поэтому сначала преобразуем, используя разность квадратов и разность кубов: ((3х + 5)4 – 4х2) + ((х + 6)3 – 1) = 0. Затем, после вынесения общего множителя, придем к простому уравнению: (х + 5)(х2 + 18х + 48) = 0. Ответ: -5; -9 ± √33. Задача. Составить многочлен третьей степени, у которого один корень, равный 4, имеет кратность 2 и корень, равный -2. Решение.По следствию из теоремы Безу, если у многочлена есть корень кратности 2 равный 4 и есть корень -2, то он без остатка должен поделиться на (х – 4)2(х + 2), значит:f(x)/((х – 4)2(х + 2)) = q(x) или f(x) = (х – 4)2(х + 2)q(x).Умножив первые две скобки, и приведя подобные слагаемые, получим: f(x) = (х3– 6x2 + 32)q(х), х3 – 6x2 + 32 – многочлен третьей степени, следовательно, q(x) – некоторое число из R (т. е. действительное). Пусть q(x) есть единица, тогда f(x) = х3 – 6x2+ 32.
Ответ: f(x) = х3 – 6x2 + 32.
ЗАКЛЮЧЕНИЕ. Тема "Уравнения и системы уравнений" - одна из ключевых тем школьного курса математики. На ней основаны темы решения неравенств и текстовых задач, аналитическое решение геометрических задач. Если говорить о практическом применении, то можно сказать, что ни одна экономическая модель не обходится без этой темы. Практически все естественные науки тем или иным образом затрагивают тему решения уравнений и систем уравнений. Знание этой темы может пригодиться учащимся в их повседневных делах.
Итак, в своём проекте я, во-первых, обобщила основные методы решения систем линейных однородных уравнений с двумя переменными, во-вторых, рассмотрела некоторые методы решения систем нелинейных уравнений с двумя переменными, в-третьих, составила решебник, который, я надеюсь, поможет читающим мой проект лучше понять тему, которую я выбрала, и сформирует навык решения систем уравнений. Другими словами я решила все задачи, которые стояли передо мной, и справилась с моей целью. Надеюсь, мой проект был интересен для чтения, повторения прошлого и знакомства с частью нового материала. Во-первых анализ вступительных экзаменов по математике показывает, что задачи на однородные уравнения и системы однородных уравнений представляют для абитуриентов определенную сложность, поэтому умение их решать во многом определяет успешную сдачу экзамена в любом ВУЗе. Во-вторых в настоящее время в различных сферах проектной деятельности (технической, экономической и др.) все шире применяют компьютерные исследования на основе модели. Под моделью понимается формализованное описание объекта, системы объектов, процесса или явления, выполненное посредством математических соотношений, набора чисел, словесных формул и т. п.. Часто описание процессов или явлений сводится к их описанию посредством линейных однородных уравнений или систем однородных уравнений. Поэтому тема проектной работы является актуальной. Познавательная ценность для данной области знаний: 1. умение решать однородные уравнения и системы однородных уравнений для дальнейшего обучения в ВУЗе. 2. применение однородных уравнений и систем однородных уравнений в проектной деятельности человека.
В научно-практической работе предметом исследования являются различного вида однородные уравнения (алгебраические, показательные, логарифмические и тригонометрические) и системы однородных уравнений. Сложность математического описания любого исследуемого объекта зависит: от необходимости одновременного рассмотрения всей совокупности факторов, отражающих свойства объекта и количества взаимосвязей. Ведущая идея: изучить существующие виды разнообразных задач содержащие однородные уравнения и системы уравнений, проанализировать их решения, а также научиться их решать различными способами.
В работе рассмотрены различные подходы к решению алгебраических, показательных, логарифмических и тригонометрических однородных уравнений и систем однородных и симметрических уравнений. В результате проведенного анализа решения данных уравнений и систем уравнений был сделан вывод о том, что наиболее часто встречающимся способом является способ замены общей части текущей переменной. Информационные источники.
1. Дорофеев Г. В. Математика. Алгебра. Функции. Анализ данных. – М.: Дрофа,2001.
2. Ионин В. Л. Системы однородных уравнений. Квант, № 9, 1975.
3. Шахмейстер А. Х. Системы уравнений. – С-Пб.: ЧеРо–на–Неве, 2004.
4. А.Х.Шахмейстер: «Системы уравнений математика»
5. Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков "АЛГЕБРА. Учебник для 9 класса с углублённым изучением математики" Москва 2006 год, 5-е издание - М.:Мнемозина, 439 страница.
6. М.Л.Галицкий, А.М.Гольдман, Л.И.Звавич "Сборник задач по алгебре 8-9 классы" Москва "Просвещение" 1994 год, 271 страница.
7. http://eqworld.ipmnet.ru
8. http://www.exponenta.ru
9. http://methmath.chat.ru
10. http://ru.wikipedia.org
11. http://www.bymath.net







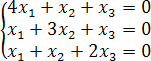 .
. система имеет только нулевое решение
система имеет только нулевое решение 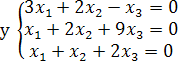 .
. матрица системы.
матрица системы.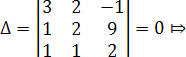 система имеет отличные от нуля решения.
система имеет отличные от нуля решения.









