Муниципальное автономное общеобразовательное учреждение "Лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина"
Индивидуальный проект
по теме:
«Теорема Морли»
Выполнил:
Учащийся «10-А» класса
Березняк Андрей Александрович
Подпись__________
Научный руководитель:
Андрющенко Алла Рудольфовна
Учитель математики
Тамбов, 2021
Оглавление
| 1. Введение…………………………………………………………………… | 3 |
| 2. Основная часть…………………………………………………………… | 4 |
| 2.1. История изучения теоремы Морлея……………………………………. | 5 |
| 2.2. Доказательства теоремы Морлея……………………………………….. | 6 |
| 2.3.Применение теоремы Морлея при решении задач…………………….. | 11 |
| 2.4 Упражнения………………………………………………………………. | 13 |
| 3. Выводы …………………………………………………………………… | 16 |
| 4. Список литературы ……………………………………………………... | 17 |
Введение
Треугольник – одна из самых простых геометрических фигур: три стороны и три вершины. Еще математиками в глубокой древности были открыты и изучены многие свойства треугольников. Но оказалось, что простая геометрическая фигура таит в себе еще множество открытий. Интересные факты о треугольнике открывались на протяжении всей истории их изучения.
Первые упоминания о треугольнике и его свойствах найдены в папирусах Древнего Египта. А именно: там описан способ нахождения площади равнобедренного треугольника. В Древней Греции изучение свойств треугольника выходит на новый уровень. Пифагор открывает свою известнейшую теорему. Герон Александрийский находит формулу, выражающую площадь треугольника через его стороны; становится известным, что биссектрисы, как медианы и высоты, пересекаются в одной точке.
В XV – XVI веках особенно активно исследовались свойства треугольника. Эти исследования составили большой раздел планиметрии, получивший название «Новая геометрия треугольника».
Актуальность. Огромное количество работ по геометрии треугольника, проведённое до начала 20 века, создало впечатление, что о треугольнике уже известно всё. Тем необычнее было открытие ещё одного интересного свойства треугольника, сделанное в начале XX века известным математиком Франком Морлеем.
Теорема Морлея была впервые сформулирована в 1905 году. Данная теорема утверждает, что трисектрисы любого треугольника ABC, взятые с одной и той же стороной, пересекаются в вершинах равностороннего треугольника, называемого треугольником Морли.
Эта теорема очень интересна и сложна, поэтому нужность и важность ее изучения неоспоримы, и чтобы облегчить изучение этой теоремы я и создаю пособие для ее изучения.
Цель исследования.
Изучение теоремы Морлея, областей ее применения в решении задач, написание пособия для ее изучения.
Задачи
-
Изучить историю открытия теоремы Морлея
-
Изучить способы доказательства теоремы
-
Проанализировать область ее применения при решении различных задач
-
Создать теоретико-практическое пособие по изучению теоремы Морлея
2. Литературный обзор
2.1 История изучения теоремы Морлея
Франк Морлей (9 сентября 1860 — 17 октября 1937) — математик, внёсший большой вклад в алгебру и геометрию. Родился в городке Вудбридж в графстве Саффолк. Родители владели небольшим магазином фарфора. В 1884 году окончил Кингс-колледж в Кембридже, в 1887 году уехал в США, но оставался британским подданным. До 1900 года преподавал в Хэверфордском колледже (Пенсильвания), потом получил кафедру в Университете Джонса Хопкинса в Балтиморе. Был широко известен как математик, в 1919—1920 годах был президентом Американского математического общества, а с 1900 по 1921 год — редактором ведущего математического журнала American Journal of Mathematics.
Наиболее известным результатом Фрэнка Морли является знаменитая теорема о трисектрисах его имени, гласящая, что точки пересечения смежных трисектрис углов произвольного треугольника являются вершинами равностороннего треугольника. [1]
Доказательство теоремы о трисектрисах Морлей опубликовал в 1914 году – через 15 лет после того, как нашел его. В 1924 году он изложил это доказательство более подробно и существенно усилил первоначальный результат. Доказательство Морлея весьма элегантно, но в то же время достаточно сложно. Оно базируется на рассмотрении довольно изысканных линий – так называемых кардиоид1.
Первые элементарные доказательства теоремы Морлея были получены в 1909 году индусами М. Сатьянараяном и М. Т. Нараньенгаром. В настоящее время известно уже, по крайней мере, несколько десятков доказательств теоремы Морлея. Однако интерес к ней не затухает, и все время появляются новые доказательства, обобщения и варианты этого изящного предложения. [2]
2.2 Доказательства теоремы Морлея
У этой теоремы есть, к сожалению, один существенный «недостаток». До недавнего времени были известны лишь довольно сложные доказательства этой теоремы. Ниже предлагается три коротких доказательства, найденных не так давно.
Доказательство теоремы Морлея
Пусть АВС – данный треугольник, а треугольник XYZ образован трисектрисами углов данного треугольника (рис.1). Докажем, что треугольник XYZ равносторонний.

Рис. 1
Введем обозначения: ∠А = 3α, ∠В = 3β, ∠С = 3γ. Рассмотрим произвольный равносторонний треугольник A1B1C1 (рис. 2).

Рис. 2
Построим на стороне B1C1 треугольник A2B1C1 так, чтобы ∠A2B1C1=γ+600, а ∠A2C1B1=β+60°. Очевидно, что ∠ B1A2C1= α , так как α + β + γ = 60°.
Точно так же построим еще два треугольника A1C1B2 и A1B1C2 (см. рис.2).
Лучи A2 B1 и B2 A1 пересекутся в некоторой точке М, так как сумма углов B1A2B2 и A1B2A2 меньше 180 градусов. При этом для треугольника A2B2M выполняются условия задачи 3. Поэтому A2C1 будет биссектрисой угла B1A2B2, а B2C1 будет биссектрисой угла A1B2A2. Это означает, что ∠ C1A2B2 = α, а ∠C1B2A2= β.
Аналогичный результат получается и в остальных случаях (для A2B1, C2B1, C2A1 и B2A1).
Таким образом, оказывается, что в треугольнике A2B2C2 проведены трисектрисы, и они при своем пересечении определяют равносторонний треугольник. Но очевидно, что треугольники A2B2C2 и АВС подобны (по углам). Следовательно, и треугольник XYZ также равносторонний. Теорема Морлея доказана. [3]
Доказательство Конвея
Пусть углы исходного треугольника равны 3α, 3β, 3γ. Введем удобное обозначение: будем писать ϕ∗ вместо ϕ + 60°. Тогда α + β + γ = 0∗. Заметим, что существуют треугольники с углами (0∗, 0∗, 0∗), (α, β∗, γ∗), (α∗, β, γ∗), (α∗, β∗, γ), (α∗∗, β, γ), (α, β∗∗, γ), (α, β, γ∗∗), так как в каждом случае сумма углов равна 180°. Теперь для каждой тройки углов построим конкретный треугольник с этими углами, специально подбирая длины сторон.
Для тройки (0∗, 0∗, 0∗) это будет равносторонний треугольник со стороной 1.
Для тройки (α∗, β, γ∗) – это треугольник, в котором сторона, соединяющая вершины с углами α∗ и γ∗, равна 1 (рис.3, а). Аналогично поступим с тройками (α, β∗, γ∗) и (α∗, β∗, γ).
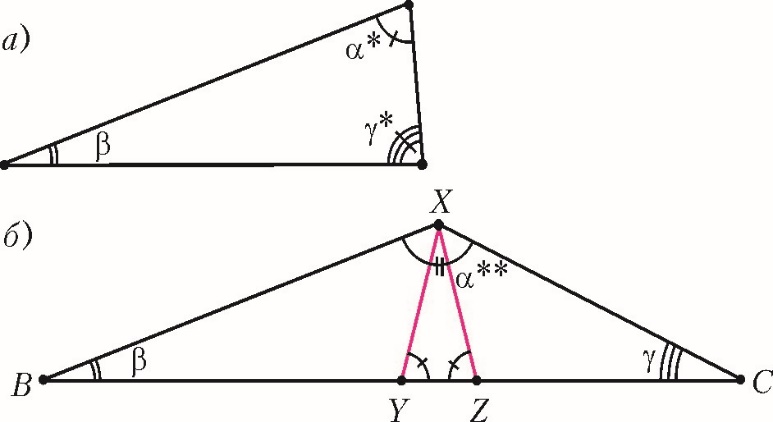
Рис 3
Для тройки (α∗∗, β, γ) сделаем так. Рассмотрим треугольник BXC (рис.3, б), в котором угол при вершине B равен β, при вершине X равен α∗∗, а при вершине C равен γ. Через вершину X проведем два луча, которые пересекают прямую BC в точках Y и Z под углом α∗, и подберем масштаб так, чтобы XY = XZ = 1. При этом сторона BX окажется равной стороне, лежащей против угла α∗ в уже построенном треугольнике с углами α∗, β, γ∗. Аналогично построим треугольники и для двух оставшихся троек такого вида.
Итак, мы получили 7 треугольников. Расположим их как показано на рисунке 4, и начнем придвигать их друг к другу, чтобы получился рисунок 5. Почему все так хорошо совпадет? Во-первых, суммы углов при всех внутренних вершинах равны 360°. Во-вторых, красный треугольник примыкает к зеленым по единичным отрезкам, а желтые треугольники примыкают к зеленым по равным отрезкам по построению (выше мы доказали это для треугольника BXC и треугольника с углами α∗, β, γ∗, аналогично рассматривается любая пара из желтого и зеленого треугольников).

Рис. 4

Рис. 5
Образовавшийся треугольник ABC подобен исходному по трем углам, а получившаяся картинка совпадает с той, что получится при проведении трисектрис. Поэтому и в исходном треугольнике образованный трисектрисами треугольник будет равносторонним. [3]
2.3 Применение теоремы Морлея при решении задач
Задача 1
Д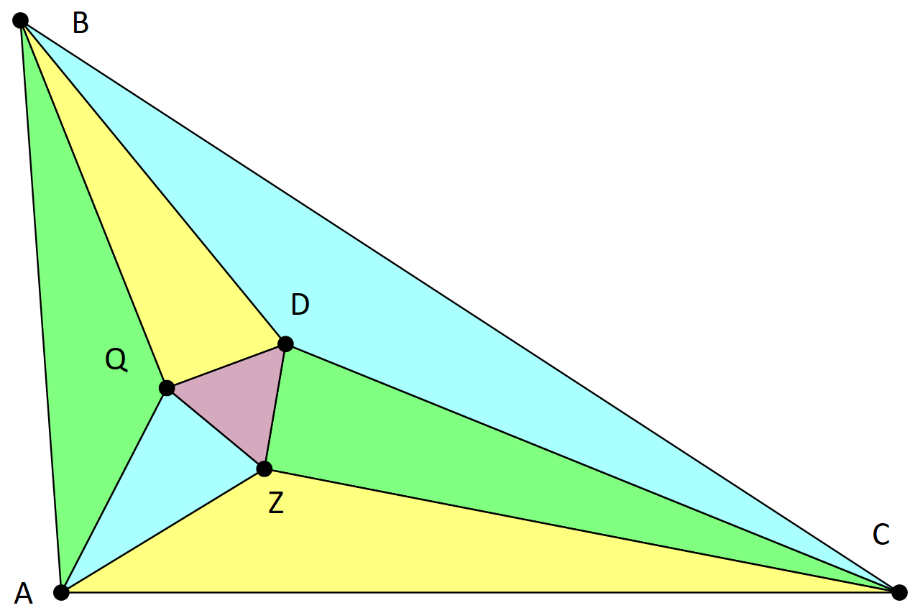 ано: ΔABC, AZ, CZ, AQ, BQ, CD, BD трисектрисы, QD=12.
ано: ΔABC, AZ, CZ, AQ, BQ, CD, BD трисектрисы, QD=12.
Найти: SΔZQD
Рис. 6
Решение:
1)По теореме Морли ΔZQD равносторонний так как AZ, CZ, AQ, BQ, CD, BD трисектрисы.
2)По формуле площади равностороннего треугольника S=√3 * QD /4=√3
Ответ:36√3
Задача 2
Д ано: ΔABC равносторонний, AZ, CZ, AQ, BQ, CD, BD трисектрисы.
ано: ΔABC равносторонний, AZ, CZ, AQ, BQ, CD, BD трисектрисы.
Доказать: ΔAZQ=ΔBQD= ΔCZD.
Рис.7
Решение:
1)Так как ΔABC равносторонний, то все углы, образованные трисектрисами равны. Следовательно, ZAC=ZAQ=QAB=ZCA=ZCD=DCB=CBD=DBQ=QBA
2)Рассмотрим ΔAZC, ΔBQA и ΔCDB они равны так как AC=AB=BC по свойству равностороннего треугольника
ZAC=ZAQ=QAB=ZCA=ZCD=DCB=CBD=DBQ=QBA Следовательно, ΔAZC=ΔBQA=ΔCDB
3)ΔAZC=ΔBQA=ΔCDB следует AZ=ZC=AQ=BQ=DB=CD
4)Рассмотрим ΔAZQ, ΔBQD и ΔCZD
AZ=ZC=AQ=BQ=DB=CD
AC=AB=BC по свойству равностороннего треугольника
Следовательно, ΔAZQ=ΔBQD= ΔCZD.
2.4 Упражнения
1. Дано ΔABC AZ, CZ, AQ, BQ, CD, BD трисектрисы углов ΔABC, QD=12. Найдите площадь ΔZQD.
2. Дано ΔABC равносторонний, AZ, CZ, AQ, BQ, CD, BD трисектрисы углов ΔABC.
Докажите: ΔAZQ=ΔBQD= ΔCZD.
3. Дано ΔABC равнобедренный AC основание, AZ, CZ, AQ, BQ, CD, BD трисектрисы углов ΔABC, угол AZC=140.
Докажите: ΔAZQ=ΔBQD= ΔCZD.
4. Дано ΔABC равнобедренный AC основание, BQ трисектриса, прилегающая к стороне AB, а BD трисектриса, прилегающая к стороне BC угла ABC, ΔAZC равнобедренный угол AZC=140, угол BAQ=QAZ=ZAC.
Докажите: ΔAZQ=ΔBQD= ΔCZQ.
5. Дано ΔABC равнобедренный AC основание, BQ трисектриса, прилегающая к стороне AB, а BD трисектриса, прилегающая к стороне BC угла ABC, ΔAZC равнобедренный угол AZC=150, угол BAQ=QAZ=ZAC, QD=12, AC=36, AQ=13.
Найдите площадь четырехугольника AQZC.
6. Дано ABCD ромб, BQ трисектриса, прилегающая к стороне AB, а BW трисектриса, прилегающая к стороне BC угла ABC, ΔAZC равнобедренный угол AZC=160, угол BAQ=QAZ=ZAC, DK трисектриса, прилегающая к стороне AD, а DF трисектриса, прилегающая к стороне DC угла ADC, ΔAJC равнобедренный угол AJC=160, угол BAQ=QAZ=ZAC.
Докажите QW параллельна KF.
7. Дано ABCD ромб, BQ трисектриса, прилегающая к стороне AB, а BW трисектриса, прилегающая к стороне BC угла ABC, ΔAZC равнобедренный угол AZC=156, угол BAQ=QAZ=ZAC, DK трисектриса, прилегающая к стороне AD, а DF трисектриса, прилегающая к стороне DC угла ADC, ΔAJC равнобедренный угол AJC=156, угол BAQ=QAZ=ZAC.
Докажите QWFK-параллелограмм.
8. Дано ABCD ромб, BQ – трисектриса, прилегающая к стороне AB, а BW трисектриса, прилегающая к стороне BC угла ABC, ΔAZC равнобедренный угол AZC=156, угол BAQ=QAZ=ZAC, DK трисектриса, прилегающая к стороне AD, а DF трисектриса, прилегающая к стороне DC угла ADC, ΔAJC равнобедренный угол AJC=156, угол BAQ=QAZ=ZAC.
Докажите QWFK-прямоугольник.
9. Дано ABCD прямоугольник, BQ – трисектриса, прилегающая к стороне AB, а BW трисектриса, прилегающая к стороне BC угла ABC, ΔAZC равнобедренный угол AZC=150, угол BAQ=QAZ=ZAC, DK трисектриса, прилегающая к стороне AD, а DF трисектриса, прилегающая к стороне DC угла ADC, ΔAJC равнобедренный, угол AJC=150, угол BAQ=QAZ=ZAC.
Докажите, что QWFK-прямоугольник.
10. Дано ABCD прямоугольник, BQ трисектриса, прилегающая к стороне AB, а BW трисектрис, а прилегающая к стороне BC угла ABC, ΔAZC равнобедренный угол AZC=150, угол BAQ=QAZ=ZAC, DK трисектриса прилегающая к стороне AD, а DF трисектриса прилегающая к стороне DC угла ADC, ΔAJC равнобедренный, угол AJC=150, угол BAQ=QAZ=ZAC, QW=12, AC=36, AQ=13.
Докажите, что QWFK-прямоугольник и найдите его периметр.
11. Дано ABCD ромб, BQ трисектриса, прилегающая к стороне AB, а BW трисектриса, прилегающая к стороне BC угла ABC, ΔAZC равнобедренный угол AZC=154, угол BAQ=QAZ=ZAC, DK трисектриса прилегающая к стороне AD, а DF трисектриса прилегающая к стороне DC угла ADC, ΔAJC равнобедренный угол AJC=150, угол BAQ=QAZ=ZAC, QW=12, AC=36, AQ=13.
Докажите, что QWFK - прямоугольник и найдите его площадь.
12. Дано ΔABC AZ, CZ, AQ, BQ, CD, BD трисектрисы углов ΔABC, углы AZC=140, AQB=168. Найдите углы Δ ABC. (задача с трисектрисами)
13. Дано ΔABC AZ, CZ, AQ, BQ, CD, BD трисектрисы углов ΔABC, углы AZQ=50, DZC=90, BQD=40. Докажите ΔABC равнобедренный.
14. Дано ΔABC AZ, CZ, AQ, BQ, CD, BD трисектрисы углов ΔABC, угол ABC=3b, ACB=3c, BAC=3a, радиус описанной окружности R.
Найдите ZQ.
3. Выводы
В результате выполнения работы была достигнута поставленная цель изучить одну из самых элегантных теорем геометрии - теорему Морлея. Была исследована история открытия этой теоремы. Рассмотрены несколько современных вариантов ее доказательства. На различных задачах были исследованы возможности практического применения данной теоремы.
Полученные результаты позволили составить теоретико-практическое пособие для школьников по изучения данной теоремы и областей ее применения при решении геометрических задач. Поставленные в работе задачи выполнены полностью.
В ходе выполнения работы я узнал много нового из истории изучения трисектрис треугольника, открытии теоремы Морли, о классических и современных способах ее доказательства.
Проведенное исследование показало, что вопрос о трисектрисах треугольника и их свойствах изучен еще не всесторонне. Полученный продукт индивидуального проекта представляет интерес с точки зрения расширения наших знаний о математике.
4. Список литературы
-
Морли, Фрэнк [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 108162001, сохранённая в 10:39 UTC 13 июля 2020 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2020. — Режим доступа: https://ru.wikipedia.org/?curid=655628&oldid=108162001
-
Тоноян Г., Яглом И. , Теорема Морлея. «Квант», №8, 1978
-
Л. Штейнгарц, Снова о теореме Морлея. «Квант», №5, 2009
-
Простой и неисчерпаемый треугольник. Режим доступа: http://www.microanswers.ru/article/prostoj-i-neischerpaemij-treygolnik.html
1� Кардиоида - плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности с таким же радиусом. Получила своё название из-за схожести своих очертаний со стилизованным изображением сердца.
2












 ано: ΔABC, AZ, CZ, AQ, BQ, CD, BD трисектрисы, QD=12.
ано: ΔABC, AZ, CZ, AQ, BQ, CD, BD трисектрисы, QD=12. ано: ΔABC равносторонний, AZ, CZ, AQ, BQ, CD, BD трисектрисы.
ано: ΔABC равносторонний, AZ, CZ, AQ, BQ, CD, BD трисектрисы.




















