Проект по математике: «Красота математики».
Цель: Расширить мировоззрение учащихся, Воспитывать познавательный интерес к математике.
Задачи: 1. Подобрать и изучить необходимую дополнительную литературу по данной теме.
2. Изучить связь красоты и математики, симметрию в архитектуре, искусстве, живописи, золотое сечение и его применение в различных направлениях.
3. Экспериментальным путем доказать, что человеческое тело, и его части подчиняется золотой пропорции.
Методы и приёмы: Поисковый и исследовательский.
Содержание :
Введение.
Пропорция в искусстве.
Золотая (логарифмическая) спираль.
Золотой треугольник.
Пропорция в архитектуре.
Исследование пропорций тел учащихся 8а класса.
Пропорция в живописи.
Пропорция в музыке.
Серебряное сечение в математике.
Золотое сечение в природе.
Заключение.
Список литературных источников.
Презентационный лист.
Введение.
О красоте математики создано немало материалов. В этом проекте мы хотим продемонстрировать гармонию чисел и форм, изящество математики и её универсальность.
Дадим определение красоты.
Красота — это субъективное понятие, характеризующее нечто, обладающее набором качеств или свойств, которые доставляют человеку эстетическое удовольствие, затрагивающее зрение, слух, обоняние или осязание, а также вызывающее внутренние, душевные переживания. Не имеет определенных критериев, стандартов и классификаций.
Определение красоты из другого источника.
Красота́ — эстетическая (неутилитарная, непрактическая) категория, обозначающая совершенство, гармоничное сочетание аспектов объекта, при котором последний вызывает у наблюдателя эстетическое наслаждение. Красота является одной из важнейших категорий культуры.
Восприятие красоты (не только в науке, но и в любой человеческой деятельности) требует от человека определённого труда на приближение к высокому знанию, которое заложил автор в своё творение: будь то математическая задача, картина или музыкальное произведение.
Математика – царица всех наук, символ мудрости. Красота математики среди наук недосягаема, а красота является одним из связующих звеньев науки и искусства. Это не только стройная система законов, но и уникальное средство познания красоты.
Красота может доставлять удовольствие не только слуху и взору, но и разуму!
Красота многогранна и многолика. Она выражает высшую целесообразность устройства мира, подтверждает универсальность математических закономерностей, которые действуют одинаково эффективно и в произведениях искусства , и в научных открытиях.
Гармония означает «согласованность, соразмерность , единство частей и целого, обуславливающие внутреннюю и внешнюю формы предмета, события, явления, их совершенство». Внешне гармония может проявляться в мелодии, ритме, симметрии, пропорциональности.
Наука и искусство – два основных начала в человеческой культуре, две дополняющие друг друга формы высшей творческой деятельности человека. В истории человечества были времена, когда эти начала дружно уживались, а были времена , когда они противоборствовали.
Основная часть.
Пропорция в искусстве.
Золотое сечение - гармоничная пропорция
В математике пропорцией называют равенство двух отношений: a : b = c : d. (a*d=b*c)
Золотое деление - деление отрезка в крайнем и среднем отношении.
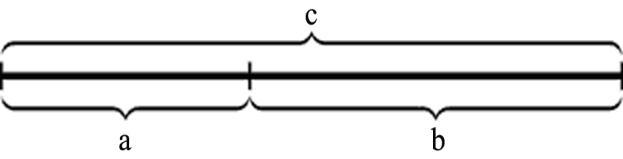
Золотое сечение – иррациональное число, приблизительно равное φ=1,6180339887.
И, наоборот, отношение меньшей части к большей =0,6180339887…
Число φ называется золотым числом.
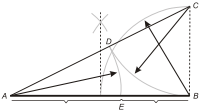
Построение золотого сечения. Золотое сечение отрезка АВ можно построить следующим образом: В точке В восстанавливают перпендикуляр к АВ, откладывают на нём отрезок ВС, равный половине АВ, на отрезке АС откладывают отрезок AD, равный АС-СВ, и наконец, на отрезке АВ откладывают отрезок АЕ, равный AD. Тогда φ==.
Золотая (логарифмическая) спираль.
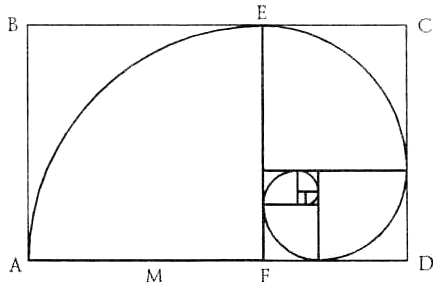
Если соединить вершины получаемых квадратов плавной линией, то получим кривую, которая называется золотой или логарифмической спиралью.
Логарифмическая спираль единственная из спиралей не меняет своей формы при увеличении размеров.
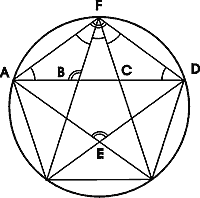
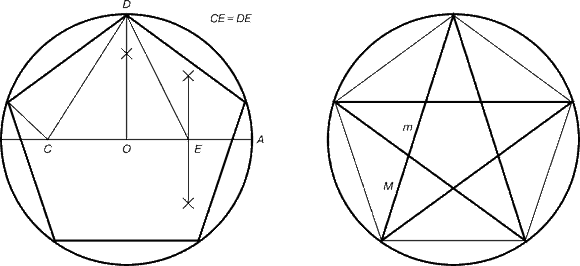
Золотой треугольник.
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.
Пропорция в архитектуре.
Под «правилом золотого сечения» в архитектуре обычно понимаются композиции, содержащие пропорции, близкие к золотому сечению. В архитектуре божественная пропорция — это мать-царица. Без нее невозможно ни ваяние скульптуры, ни создание архитектурного проекта.
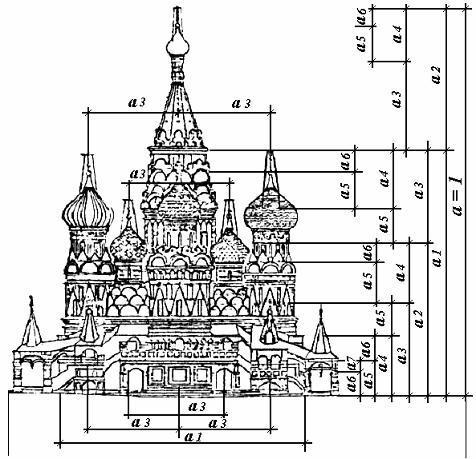 Каждый элемент храма Василяя Блаженного выполнен с соблюдением золотой пропорции.
Каждый элемент храма Василяя Блаженного выполнен с соблюдением золотой пропорции.
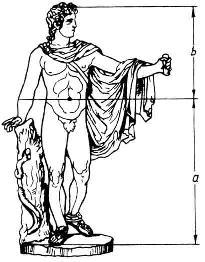
Статуя Аполлона Бельведерского, издавна почитаемая за образец мужской красоты. Если ее высоту а разделить в отношении золотого сечения (b : а 0,618) и то же самое проделать с каждой частью, то точки деления придутся на анатомически важные пункты: начало шеи, талию, коленную чашечку и т. д. Та же закономерность распространяется на лицо и руки статуи. Много позже было измерено несколько тысяч человеческих тел и обнаружено, что для них отношение длины торса до талии к длине всего тела, т. е. отношение b:а равно 0,615

Исследование пропорций тел учащихся 8а класса
«Человеческое тело – лучшая красота на земле», говорил Чернышевский Н.Г.
Вот и мы решили исследовать пропорции тел учащихся своего класса.
|
| Андрей | Ки-рилл | Юля | Нас-тя Ч. | Ари-на | Ди-ма И. | На-дя | Олег | Учи-тель |
| Рост,см | 162 | 177 | 164 | 166 | 165 | 183 | 158 | 163 | 160 |
| Окружность головы | 55 | 68 | 56 | 53 | 53 | 57 | 53 | 57 | 58 |
| Длина от макушки до пояса | 65 | 109 | 63 | 60 | 65 | 76 | 62 | 66 | 67 |
| Длина от макушки до среднего пальца | 102 | 110 | 102 | 98 | 102 | 112 | 100 | 100 | 100 |
| Длина плеча | 44 | 47 | 42 | 38 | 40 | 42 | 42 | 42 | 42 |
| Длина руки | 66 | 72 | 72 | 70 | 72 | 80 | 68 | 62 | 72 |
В исследовании приняли участие 63% учащихся класса. После необходимых измерений и несложных вычислений , мы выяснили, что пропорции тела сохраняются у многих детей, лишь у некоторых есть небольшие отклонения от значения золотой пропорции, что допустимо из-за индивидуальных особенностей человеческого тела, тем более организмы учащихся ещё полностью не сформировались.
Пропорция в живописи.
Золотое сечение находит применение и в живописи. Его называют исключительным, превосходнейшим, замечательнейшим.
Посмотрим на картину Рафаэля «Избиение младенцев». Не знаем, рисовал ли
Рафаэль золотую спираль, когда задумывал композицию этой картины, но гравер Раймонди эту спираль увидел, когда завершал эскиз Рафаэля.


Рафаэль «Избиение младенцев».
Композиция Леонардо да Винчи «Мона Лиза» основана на золотых треугольниках, которые являются частями правильного звездчатого пятиугольника.


Портрет Моны Лизы.
Пропорция в музыке.
Большинство выдающихся музыкальных сочинений можно легко разделить на части или по теме, или по интонационному строю, или по ладовому строю, которые находятся между собой в отношении золотого сечения. Не только большие части этюдов могут делиться по длительности в отношении золотого сечения, но и части этюдов внутри зачастую делятся в таком же отношении. Золотое сечение приводит к впечатлению особой стройности музыкального сочинения.
“Исчисление пропорций, которое совершается при восприятии музыки, происходит скрытным неосознанным образом” – говорил Лейбниц.
Серебряное сечение в математике.
Кроме золотой пропорции в математике существует ещё и серебряная пропорция. Целое относится к меньшему отрезку, как длина окружности к её диаметру. Примером такой пропорции служит отношение длины окружности к длине её диаметра, равное числу π. То есть = π, π ≈ 3,14.
Золотое сечение в природе.
Каждый вид растений имеет свое листорасположение, вернее, угол расхождения листьев, который характерен не только для листьев, но и для расположения веток, почек, цветов, чашек внутри почек. Но этот угол не произвольный, а подчиняется определенному закону.
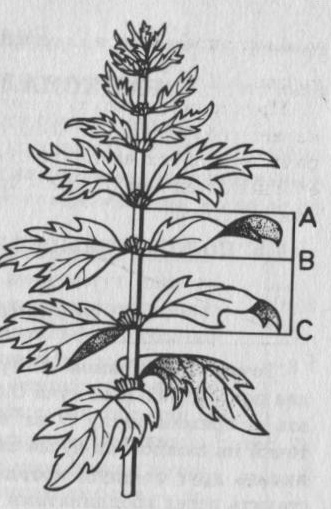

Как говорил Ж.Фурье: «Пристальное и глубокое изучение природы есть источник самых Плодотворных открытий математики».
Закономерность, похожую на золотую пропорцию можно пронаблюдать, например, в строении тела ящерицы и в стебле цикория.
Заключение.
Конечно же, все законы красоты невозможно вместить в несколько формул. Но, изучая математику мы открываем всё новые и новые слагаемые прекрасного, приближаясь к пониманию, а в дальнейшем и к созданию красоты и гармонии.
А красота многогранна и многолика. Она выражает высшую целесообразность устройства мира, подтверждает универсальность математических закономерностей, которые действуют одинаково эффективно и в произведениях искусства, и научных открытиях.
Красота помогает с радостью воспринимать окружающий мир, а математика даёт возможность осознать явления и упрочить знания о гармонии всего мира.
Искусство, наука, красота… эти великие сферы человеческой деятельности, внешне столь разные и далекие друг от друга, тесно переплетены между собой незримыми узами! И разорвать эти узы нельзя, не повредив и тому и другому. Красота является самым крепким связующим звеном между наукой и искусством!
Единство науки и искусства – важнейший залог последующего развития культуры!
Список литературных источников.
1.http://upload.wikimedia.org/wikipedia/commons/thumb/7/76/Leonardo_da_Vinci_-_Mona_Lisa.jpg/385px-Leonardo_da_Vinci_-_Mona_Lisa.jpg
2. http://luboznaiki.ru/opredelenie/krasota.html
3. http://ru.wikipedia.org
4. Математика и искусство” А. В. Волошинов, Москва, “Просвещение”, 2000.
5. Эстетика урока математики. Пособие для учителей. И.Г.Зенкевич. Москва
“Просвещение”, 1981.
6. “Математическое путешествие в мир гармонии” (устный журнал)
Е.С.Смирнова, Н.А. Леонидова (Москва). “Школа-Пресс”. Ж. “Математика в
школе” № 3, 1993.
Презентационный лист.
Проект по математике: «Красота математики».
Секция: Математика, физика, информатика.
Цель: Расширить мировоззрение учащихся, Воспитывать познавательный интерес к математике.
Задачи: 1. Подобрать и изучить необходимую дополнительную литературу по данной теме.
2. Изучить связь красоты и математики, симметрию в архитектуре, искусстве, живописи, золотое сечение и его применение в различных направлениях.
3. Экспериментальным путем доказать, что человеческое тело, и его части подчиняется золотой пропорции.
Методы и приёмы: Поисковый и исследовательский.
Выполнили: Черников Кирилл Николаевич, 8а класс, 25.11.1999г.,
Ионов Дмитрий Александрович, 8а класс, 14.03.1999г.,
Мельникова Юлия Юрьевна, 8а класс, 25.11.1999г.,
Путилин Александр Викторович, 8а класс, 10.07.1999г.
Руководитель: Ляшенко Валентина Ивановна, учитель математики
МКОУ Заболотовская СОШ.
2014г.








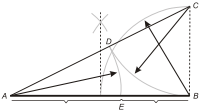



 Каждый элемент храма Василяя Блаженного выполнен с соблюдением золотой пропорции.
Каждый элемент храма Василяя Блаженного выполнен с соблюдением золотой пропорции.



























