Промежуточная аттестация по геометрии (устный экзамен) в 8 классе

Устный экзамен по геометрии 8 класс (переводной)

Билет 1

1. Какая фигура называется углом. Объяснить, что такое вершина и стороны угла. Какой угол называется развернутым? острым? прямым? тупым? Какие углы называются смежными? Свойство смежных углов. Какие углы называются вертикальными? Свойство вертикальных углов.

2. Определение параллелограмма. Свойства параллелограмма. Площадь параллелограмма

Задачи:

1. Какие из следующих утверждений верны?

1. Противоположные углы параллелограмма равны.

2. Биссектриса угла делит угол пополам.

3. Смежные углы равны.

В ответ запишите номера выбранных утверждений.

1. В остроугольном треугольнике ABC проведена высота CH, угол ABC равен 36°. Найдите угол BCH. Ответ дайте в градусах

2. Найдите площадь прямоугольника, если его периметр равен 56 и одна из его сторон на 6 больше другой.

Билет 2

1. Какая точка называется серединой отрезка? Какой луч называется биссектрисой угла? Какой отрезок называется перпендикуляром?

2. Определение трапеции. Равнобедренная трапеция, ее свойства. Прямоугольная трапеция. Площадь трапеции

Задачи:

1. Какие из следующих утверждений верны?

1. Диагонали прямоугольника равны.

2. Все равнобедренные треугольники подобны.

3. Если диагонали параллелограмма перпендикулярны, то это ромб.

В ответ запишите номера выбранных утверждений.

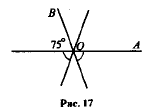1. Углы, отмеченные на рисунке 17 одной дугой, равны. Найдите угол AOB.

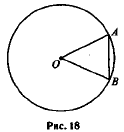1. Центральный угол опирается на хорду AB длиной 10. При этом угол AOB равен 60°. Найдите радиус окружности.

Билет 3

1. Какая фигура называется треугольником? Стороны, вершины и углы треугольника. Что такое периметр треугольника? Какой отрезок называется медианой, высотой и биссектрисой треугольника?

2. Определение прямоугольника. Свойства и признак прямоугольника. Площадь прямоугольника

Задачи:

1. Какие из следующих утверждений верны?

1. В параллелограмме сумма углов, прилежащих к одной стороне, равна 180°.

2. В тупоугольном треугольнике всегда есть два острых угла.

3. Любой параллелограмм можно вписать в окружность.

В ответ запишите номера выбранных утверждений.

1. Периметр квадрата равен 72. Найдите площадь квадрата.

2. Прямые a и b параллельны. Найдите угол 3, если угол 1 равен 40°, а угол 2 равен 34°. Ответ дайте в градусах.

Билет 4

1. Какие треугольники называются равными? Признаки равенства треугольников.

2. Определение ромба, свойства. Площадь ромба

Задачи:

1. Какие из следующих утверждений верны?

1. Касательная к окружности перпендикулярна радиусу, проведенному к точке касания.

2. Центр вписанной в треугольник окружности лежит в точке пересечения его высот.

3. Существует прямоугольник, у которого диагонали взаимно перпендикулярны.

В ответ запишите номера выбранных утверждений.

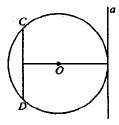1. Радиус окружности с центром в точке O равен 65, длина хорды CD равна 32. Найдите расстояние от хорды CD до параллельной ей касательной a.

1. В прямоугольнике диагональ равна 12, а угол между ней и одной из сторон равен 30°. Найдите площадь прямоугольника, деленную на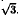

Билет 5

1. Какой треугольник называется равнобедренным? Свойство равнобедренного треугольника. Какой треугольник называется равносторонним?

2. Определение квадрата, свойства. Площадь квадрата

Задачи:

1. Какие из следующих утверждений верны?

1. В ромбе все стороны равны.

2. Вписанный угол, опирающийся на диаметр, прямой.

3. В квадрате радиус описанной окружности равен половине стороны.

В ответ запишите номера выбранных утверждений.

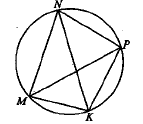1. Четырехугольник MNPK вписан в окружность. Угол MNP равен 81°. Найдите угол MNK, если угол KMP равен 64°.

2. Найдите величину угла COD, если OD - биссектриса угла AOB, угол AOB равен 86°. Ответ дайте в градусах.

Билет 6

1. Определение параллельных прямых. Секущая. Признаки параллельности двух прямых

2. Площадь треугольника. Формула Герона. Площадь равностороннего треугольника, площадь прямоугольного треугольника

Задачи:

1. Какие из следующих утверждений верны?

1. Все хорды окружности равны между собой.

2. Если один из двух смежных углов острый, то другой – тупой.

3. У любой трапеции основания параллельны.

В ответ запишите номера выбранных утверждений.

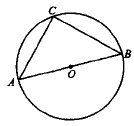1. Найдите градусную меру угла BAC, если известно, что AB является диаметром окружности, а градусная мера угла AOC равна 90°.

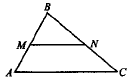2. В треугольнике ABC MN - средняя линия. Площадь треугольника MBN равна 17. Найдите площадь треугольника ABC.

Билет 7

1. Определение окружности. Центр, радиус, хорда и диаметр окружности.

2. Теорема Пифагора

Задачи:

1. Какие из следующих утверждений верны?

1. Средняя линия трапеции равна полуразности оснований.

2. У любой прямоугольной трапеции есть два равных угла.

3. Вертикальные углы равны.

В ответ запишите номера выбранных утверждений.

Четырехугольник MKPN описан около окружности, MK=15, KP=18, MN=9. Найдите NP.

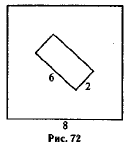1. Из квадрата вырезали прямоугольник. Найдите площадь получившейся фигуры.

Билет 8

1. Сформулируйте теорему о сумме углов треугольника. Какой угол называется внешним углом треугольника? Свойство внешнего угла.

2. Определение подобных треугольников. Отношение площадей и периметров подобных треугольников

Задачи:

1. Какие из следующих утверждений верны?

1. Если углы при основании трапеции равны, то эта трапеция – равнобедренная.

2. Треугольник со сторонами 1, 3 и 5 существует.

3. Сумма углов выпуклого четырехугольника равна 360°.

В ответ запишите номера выбранных утверждений.

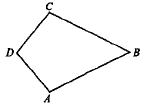1. В выпуклом четырехугольнике ABCD AD = CD, AB = BC, угол B равен 76°, угол D равен 100°. Найдите угол A. Ответ дайте в градусах.

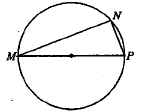2. Прямоугольный треугольник MNP с катетами 18 см и 24 см вписан в окружность. Чему равен радиус этой окружности? Ответ дайте в сантиметрах.

Билет 9

1. Какой треугольник называется остроугольным? тупоугольным? прямоугольным? Как называются стороны прямоугольного треугольника? Свойства прямоугольных треугольников.

2. Признаки подобия треугольников

Задачи:

1. Какие из следующих утверждений верны?

1. Косинус острого угла прямоугольного треугольника равен отношению прилежащего к этому углу катета к гипотенузе.

2. Каждая из биссектрис равнобедренного треугольника является его высотой.

3. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

В ответ запишите номера выбранных утверждений.

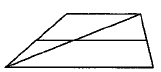1. Основания трапеции равны 5 и 12. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

2. Окружность с центром в точке O описана около равнобедренного треугольника ACD, в котором угол ACD равен 43°. Найдите величину угла COA. Ответ дайте в градусах.

Билет 10

1. Аксиома параллельных прямых

2. Синус, косинус и тангенс острого угла прямоугольного треугольника

Задачи:

1. Какие из следующих утверждений верны?

1. Отношение площадей подобных треугольников равно коэффициенту подобия.

2. Одна из биссектрис равнобедренного треугольника является его медианой.

3. Диаметр окружности – самая большая из хорд этой окружности.

В ответ запишите номера выбранных утверждений.

1. Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.

2. Углы выпуклого четырехугольника относятся как 1 : 3 : 5 : 6. Найдите меньший угол. Ответ дайте в градусах.

Билет 11

1. Касательная к окружности. Определение, свойство

2. Центральные и вписанные углы. Определение и свойства

Задачи:

1. Какие из следующих утверждений верны?

1. Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы.

2. Расстояние от любой точки на окружности до центра окружности равно радиусу этой окружности.

3. Площадь ромба равна квадрату его стороны.

В ответ запишите номера выбранных утверждений.

1. Величина центрального угла AOC равна 100°. Найдите величину вписанного угла ACD. Ответ дайте в градусах.

2. Один угол параллелограмма в 3 раза больше другого. Найдите меньший угол. Ответ дайте в градусах.

Билет 12

1. Вписанная и описанная окружности. Определение и свойства

2. Соотношения между сторонами и углами треугольника. Неравенство треугольника

Задачи:

1. Какие из следующих утверждений верны?

1. Тангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему.

2. Площадь трапеции равна произведению средней линии на высоту.

3. Угол, вершина которого лежит в центре окружности, называется центральным.

В ответ запишите номера выбранных утверждений.

1. В прямоугольнике периметр равен 55, а отношение смежных сторон равно 3 : 8. Найдите площадь прямоугольника.

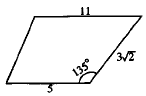Основания трапеции равны 5 и 11, одна из боковых сторон равна 3√2, а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.