Муниципальное бюджетное общеобразовательное учреждение
Кормиловского муниципального района
Юрьевская средняя общеобразовательная школа
|
| «Согласовано»
/____________________/ Боднар В.Н. (завуч по учебной работе)
«_____»___________20 г
| «Утверждаю»
/____________________/ Кейвабу Т.С. (директор школы)
«_____»___________20 г
|
|
|
|
|
Рабочая программа
по алгебре и началам
математического анализа
для 11 класса
(профильный уровень)
Составлена по УМК Т.А. Бурмистровой
к учебнику Ю.М. Колягина и др.
«Алгебра и начала математического анализа»
Разработала: Касаткина Е.В.
учитель математики
2021 г.
Пояснительная записка
Данная рабочая программа составлена на основе:
- Федерального закона Российской Федерации «Об образовании в Российской Федерации» (от 29.12.2012 № 273-ФЗ).
- федерального компонента государственного стандарта среднего (полного) общего образования по математике (профильный уровень) 2004 г. (приказ Министерства образования Российской Федерации от 05.03.2004 № 1089 «Об утверждении федерального компонента государственных стандартов начального общего, основного общего и среднего (полного) общего образования».)
-учебного плана школы (Приказ Министерства образования Российской Федерации от 09.03.2004 № 1312 «Об утверждении федерального базисного учебного плана и примерных учебных планов для образовательных учреждений Российской Федерации, реализующих программы общего образования», Приказ Министерства образования и науки Российской Федерации от 30.08.2010 № 889 «О внесении изменений в федеральный базисный учебный план и примерные учебные планы для образовательных учреждений Российской Федерации, реализующих программы общего образования, утверждённые приказом Министерства образования Российской Федерации от 09.03.2004 № 1312 «Об утверждении федерального базисного учебного плана и примерных учебных планов для образовательных учреждений Российской Федерации, реализующих программы общего образования»).
- перечня учебников , допущенных к использованию в 2020-2021 учебном году (Приказ Министерства образования и науки Российской Федерации от от 31 марта 2014 г. № 253 «Об утверждении федерального перечня учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования» ).
- примерной программы среднего (полного) общего образования по математике на профильном уровне (Т.А.Бурмистрова Сборник программ общеобразовательных учреждений. Алгебра и начала математического анализа.10-11 классы., , Москва «Просвещение» 2019 г.);
- программы по алгебре и началам математического анализа для 11 класса (профильный уровень) авторов Ю.М.Колягин, М.В.Ткачева, М.И.Шабунин, Н.Е.Фёдорова (Т.А.Бурмистрова Сборник программ общеобразовательных учреждений. Алгебра и начала математического анализа.10-11 классы., , Москва «Просвещение» 2010 г.)
Рабочая программа ориентирована на использование учебного комплекта:
- учебника Ю. М. Колягин, М. В. Ткачева и др . «Алгебра и начала математического анализа: базовый и углубленный уровни , 11 класс» (М: Просвещение, 2014г.);
- книги для учителя Е.Н.Фёдорова, М.В.Ткаченко «Изучение алгебры и начал математического анализа в 11 классах», Москва, «Просвещение»,2008 г.
- «Алгебра и начала математического анализа:. Дидактические материалы для 11 класса (профильный уровень)» (М.И.Шабунин, М.В.Ткачева, Н.Е.Фёдорова, О.Н.Доброва, М.:Просвещение,2010г)
- Алгебра и начала математического анализа. Тематические тесты. 11 класс. (базовый и профильный уровни) Ткачёва М.В. (2010г.,)
Общая характеристика учебного предмета.
В профильном курсе содержание образования, представленное в старшей школе, развивается в следующих направлениях:
· систематизация сведений о числах; формирование представлений о расширении числовых множеств от натуральных до комплексных как способе построения нового математического аппарата для решения задач окружающего мира и внутренних задач математики; совершенствование техники вычислений;
· развитие и совершенствование техники алгебраических преобразований, решения уравнений, неравенств, систем;
· систематизация и расширение сведений о функциях, совершенствование графических умений; знакомство с основными идеями и методами математического анализа в объеме, позволяющем исследовать элементарные функции и решать простейшие геометрические, физические и другие прикладные задачи;
· расширение системы сведений о свойствах плоских фигур, систематическое изучение свойств пространственных тел, развитие представлений о геометрических измерениях;
· развитие представлений о вероятностно-статистических закономерностях в окружающем мире;
· совершенствование математического развития до уровня, позволяющего свободно применять изученные факты и методы при решении задач из различных разделов курса, а также использовать их в нестандартных ситуациях;
· формирование способности строить и исследовать простейшие математические модели при решении прикладных задач, задач из смежных дисциплин, углубление знаний об особенностях применения математических методов к исследованию процессов и явлений в природе и обществе.
Изучение математики в старшей школе на профильном уровне направлено на достижение следующих целей:
· формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов;
· овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественнонаучных дисциплин, для продолжения образования и освоения избранной специальности на современном уровне;
· развитие логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности;
· воспитание средствами математики культуры личности: знакомство с историей развития математики, эволюцией математических идей, понимание значимости математики для общественного прогресса.
Место предмета в базисном учебном плане
Согласно Федеральному базисному учебному плану для общеобразовательных учреждений Российской Федерации на изучение предмета «Математика» на профильном уровне отводится 408 учебных часов: 204 часа в 10 классе и 204 часа в 11 классе из расчета 6 часов в неделю (4 часа алгебры и 2 часа геометрии). Данная рабочая программа по алгебре и началам математического анализа для 11 класса( профильный уровень) рассчитана на 4 часа в неделю, всего 136 учебных часов в год.
Требования к уровню подготовке выпускников:
Знать (понимать)
-
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
-
значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки, историю развития геометрии;
-
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
-
различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
-
роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания, для практики.
Уметь
-
проводить доказательные рассуждения в ходе решения задач;
-
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
-
составлять уравнения и неравенства по условию задачи;
-
использовать для приближенного решения уравнений и неравенств графический метод;
Содержание образования
1. Тригонометрические функции-19 часов
Область определения и множество значений тригонометрических функций. Четность, нечетность, периодичность тригонометрических функций. Свойства функции у = cosх: и ее график. Свойства функции у = sinх; и ее график. Свойства функции у = tgx и ее график. Обратные тригонометрические функции.
Основная цель — изучить свойства тригонометрических функций, научить учащихся применять эти свойства при решении уравнений и неравенств; обобщить и систематизировать знания об исследовании функций элементарными методами1', научить строить графики тригонометри ческих функций, используя различные приемы построения графиков.
Среди тригонометрических формул следует особо выделить те формулы, которые непосредственно относятся к исследованию тригонометрических функции и построению их графиков. Так, формулы sin(-х) = -sin х и cos(-x) = cos х выражают свойства нечетности и четности функций у = sin х и у = cos х соответственно.
На профильном уровне продолжается изучение свойств элементарных функций методами элементарной математики; решаются задачи разного уровня сложности на нахождение области определения и множества значений сложных функций.
На углубленном уровне рассматриваются доказательства утверждений, являющихся отрицанием факта ограниченности функции, периодичности и пр. Логическая структура этих доказательств специально не обсуждается. Приведенные примеры рассуждений в задачах позволяют провести их анализ и направить в нужное русло поиск учащихся при самостоятельном выполнении упражнений.
Построение графиков тригонометрических функций проводится с использованием их свойств и начинается с построение графика функции у = cosх.
С помощью графиков тригонометрических функций решаются простейшие тригонометрические уравнения и неравенства.
На базовом уровне обратные тригонометрические функции даются в ознакомительном плане. Рекомендуется также рассмотреть графики функций у = |cosх|, у = а + cosх , у = cos (х + а),
у = acos х, у = cos ах, где а — некоторое число.
На профильном уровне обратные тригонометрические функции изучаются после повторения понятия\взаимно обратных функций. Применение свойств обратных тригонометрических функций рассматривается на конкретных примерах.
В ходе изучения темы особое внимание уделяется исследованию функций и построению графиков методами элементарной математики. Таким образом, при изучении данного раздела происходит как обобщение и систематизация знаний учащихся об элементарных функциях и их исследовании методами элементарной математики, так и подготовка к восприятию элементов математического анализа.
2. Производная и ее геометрический смысл-22 часа
Предел последовательности. Предел функции. Непрерывность функции. Определение производной. Правила дифференцирования. Производная степенной функции. Про- ' изводные элементарных функций. Геометрический смысл производной.
Основная цель — ввести понятие предела последовательности, предела функции, производной; научить наводить производные с помощью формул дифференцирования; научить находить уравнение касательной к графику ; функции, решать практические задачи на применение понятия производной.
На базовом уровне изложение материала ведется на наглядно-интуитивном уровне: многие формулы не доказывается, а только поясняются или принимаются без доказательств. Главное — показать учащимся целесообразность , изучения производной и в дальнейшем первообразной (интеграла), так как это необходимо при решении многих практических задач, связанных с исследованием физических явлений, вычислением площадей криволинейных фигур и объемов тел с произвольными границами, с построением графиков функций. Прежде всего следует показать, что функции, графиками которых являются кривые, описывают многие важные физические и технические процессу.
На профильном уровне учащиеся знакомятся со строгими определениями предела, последовательности, предела функции, непрерывности функции. Правила дифференцирования и формулы производных элементарных функций доказываются строго.
Достаточно подробное изучение теории пределов числовых последовательностей учащимися профильных классов не просто готовит их к восприятию сложного понятия предела функции в точке, но развивает многие качества мыслительной деятельности учащихся.
3. Применение производной к исследованию функций-16 часов
Возрастание и убывание функции. Экстремумы функции. Наибольшее и наименьшее значения функции. Производная второго порядка, выпуклость и точки перегиба. Построение графиков функций.
Основная цель — показать возможности производной в исследовании свойств функций и построении их графиков.
При изучении материала широко используются знания, полученные учащимися в ходе работы над предыдущей темой.
Обосновываются утверждения о зависимости возрастания и убывания функции от знака ее производной на данном промежутке. Вводятся понятия точек максимума и минимума, точек перегиба. Учащиеся знакомятся с новыми терминами: критические и стационарные точки.
После введения понятий максимума и минимума функции формируется представление о том, что функция может иметь экстремум в точке, в которой она не имеет производной, например, у = |х| в точке х = 0.
Определение вида экстремума предполагается связать с переменой знака производной функции при переходе через точку экстремума. Необходимо показать учащимся не только профильных классов, что это можно сделать проще — по знаку второй производной: если f"(x) 0 в некоторой стационарной точке х, то рассматриваемая стационарная точка есть точка минимума; если f"(x) f"(x) = 0, то точка х есть точка перегиба.
Приводится схема исследования основных свойств функции, предваряющая построение графика. В классах базового уровня эта схема выглядит так:
1) область определения функции;
2) точки пересечения графика с осями координат;
3) производная функции и стационарные точки;
4) промежутки монотонности;
5) точки экстремума и значения функции в этих точках.
На профильном уровне (после изучения второй производной) схема исследования функции выглядит так:
1) область определения функции; четность (нечетность); периодичность;
2) нули функции; промежутки знакопо- стоянства;
3) асимптоты графика функции;
4) первёя производная; критические точки; промежутки монотонности; экстремумы;
5) вторая производная; промежутки выпуклости, направления выпуклостей и точки перегиба.
4. Первообразная и интеграл-15 часов.
Первообразная. Правила нахождения первообразных. Площадь криволинейной трапеции. Интеграл и его вычисление. Вычисление площадей фигур с помощью интегралов. Применение интегралов для решения физических задач. Простейшие дифференциальные уравнения.
Основная цель — ознакомить с понятием интеграла и интегрированием как операцией, обратной дифференцированию; научить находить площадь криволинейной трапеции, решать простейшие физические задачи с помощью интеграла.
Операция интегрирования сначала определяется как операция, обратная дифференцированию, далее вводится понятие первообразной, при этом не вводится ни определение неопределенного интеграла, ни его обозначение. Таблица правил интегрирования (т. е. таблица первообразных) в этом случае естественно получается из таблицы производных. Формулируется утверждение, что все первообразные для функции f(x) имеют вид F(x) + С, где F(x) — первообразная, найденная в таблице. Этот факт не доказывается, а только поясняется.
Связь между первообразной и площадью криволинейной трапеции устанавливается формулой Ньютона — Лейбница. Далее возникает определенный интеграл как предел ин- , тегральной суммы; при этом формула Ньютона — Лейбница также оказывается справедливой. Таким образом, эта формула является главной: с ее помощью вычисляются определенные интегралы и находятся площади криволинейных трапеций.
На профильном уровне учащиеся знакомятся с задачами на нахождение пути по заданной скорости, на вычисление работы переменной силы, задачами о размножении бактерий и о радиоактивном распаде более подробно, чем школьники классов базового уровня, и учатся решать простейшие дифференциальные уравнения.
5. Комбинаторика-10 часов
Математическая индукцця. Правило произведения. Размещения с повторениями. Перестановки. Размещения без повторений. Сочетания без повторений и бином Ньютона.
Основная цель — развить комбинаторное мышление учащихся; ознакомить с теорией соединений (как самостоятельным разделом математики и в дальнейшем — с аппаратом решения ряда вероятностных задач); обосновать формулу бинома Ньютона (с которой учащиеся лишь ' знакомились в курсе 10 класса).
Основными задачами комбинаторики считаются следующие: 1) составление упорядоченных множеств (образование перестановок); 2) составление подмножеств данного множества (образование сочетаний); 3) составление упорядоченных подмножеств данного множества (образование размещений).
Из всего многообразия вопросов, которыми занимается комбинаторика, в содержание образования старшей школы сегодня включается лишь теория соединений — комбинаторных конфигураций, которые называются перестановками, размещениями и сочетаниями. Причем обязательными для изучения являются лишь соединения без повторений — соединения, составляемые по определенным правилам из различных элементов.
Теория соединений с повторениями не является обязательной для изучения даже на профильном уровне, тем не менее, полезно ввести понятие хотя бы размещений с повторениями, так как задачи на подсчет числа этих размещений рассматриваются уже на первых уроках при решении задач на применение правила произведения.
Знакомство с остальными соединениями с повторениями может быть рассмотрено с учащимися профильных классов при наличии времени. Доказательство же справедливости формул для подсчета числа перестановок с повторениями и числа сочетаний с повторениями следует рассматривать только при углубленном изучении с учащимися, усвоившими применение метода мате- матической индукции.
Дополнительной мотивацией рассмотрения, например, перестановок с повторениями является то, что биномиальные коэффициенты есть не что иное, как перестановки с повторениями. Поэтому учащиеся, знакомые с понятием перестановок с повторениями, легко воспринимают вывод формулы бинома Ньютона.
-
Элементы теории вероятностей-8 часов
Вероятность события. Сложение вероятностей. Условная вероятность. Независимость событий. Вероятность произведения независимых событий. Формула Бернулли.
Основная цель — сформировать понятие вероятности случайного независимого события; научить решать задачи на применение теоремы о вероятности суммы двух несовместных событий и на нахождение вероятности произведения двух независимых событий.
В программу включено изучение (частично на интуитивном уровне) лишь отдельных элементов теории вероятностей. При этом введению каждого понятия предшествует неформальное объяснение, раскрывающее сущность данного понятия, его происхождение и реальный смысл. Так вводятся понятия случайных, достоверных и невозможных событий, связанных с некоторым испытанием; определяются и иллюстрируются операции над событиями.
Классическое определение вероятности события с рав- новозможными элементарными исходами формулируется строго, и на его основе (с использованием знаний комбинаторики) решается большинство задач/Понятия геометрической вероятности и статистической вероятности вводились на интуитивном уровне в основной школе.
Независимость событий вводится достаточно строго (после определения понятия условной вероятности). Разбирается решение задачи на нахождение вероятности события В, состоящего в том, что при п испытаниях наблюдаемое событие А произойдет ровно k раз, после чего обосновывается формула Бернулли.
При изложении материала данного раздела подчеркивается прикладное значение теории вероятностей в различных областях знаний и практической деятельности человека.
-
Комплексные числа-13 часов
Определение комплексных чисел. Сложение и умножение комплексных чисел. Комплексно сопряженные числа. Модуль комплексного числа. Операции вычитания и деления. Геометрическая интерпретация комплексного числа. Тригонометрическая форма комплексного числа. Умножение и деление комплексных чисел, записанных в тригонометрической форме. Формула Муавра. Квадратное уравнение с комплексным неизвестным. Извлечение корня из , комплексного числа. Алгебраические уравнения.
Основная цель — научить представлять комплексное число в алгебраической и тригонометрической формах; изображать число на комплексной плоскости; научить выполнять операции сложения,t вычитания, умножения и де- 1 ления чисел, записанных в алгебраической форме, операции умножения и деления чисел, представленных в тригонометрической форме.
На примере теории комплексных чисел старшеклассни- 1 ки впервые (а, возможно, и вообще единственный раз) знакомятся со строгим построением теории чисел.
Комплексные числа вводятся либо как упорядоченная пара чисел, либо как выражение а + bi, где а и b — действительные числа, i — некоторый символ, такой, что i2 = -1. Затем формулируются правила, устанавливающие равенство комплексных чисел, вводятся числа, соответствующие привычным для школьников нулю и единице, изучаются правила арифметических действий над комплексными числами.
Тригонометрическая интерпретация комплексного числа позволяет решать алгебраические уравнения (в частности, квадратные) в поле комплексных чисел и осознанно воспринимать основную теорему алгебры,.которая формулируется в конце темы.
8. Повторение курса алгебры и начал математического анализа (Уравнения и неравенства. Задачи с параметром )-21 час
Методы решения уравнений с одним неизвестным. Приёмы решения уравнений с двумя неизвестными. Неравенства, системы и совокупности неравенств с одним неизвестным. Методы их решения. Способы и методы решения систем уравнений с двумя неизвестными. Изображение на координатной плоскости решений неравенств и систем неравенств с двумя неизвестными. Подходы к решению задач с параметром.
Основная цель — обучить приемам решения уравнений, неравенств и систем уравнений и неравенств с двумя переменными.
Изображение множества точек, являющегося решением уравнения первой степени с двумя неизвестными, не ново для учащихся старших классов. Решение систем уравнений с помощью графика знакомо школьникам с основной колы. Теперь им предстоит углубить знания, полученные ранее, и ознакомиться с решением неравенств с двумя переменными и их систем.
Учебный материал этой темы построен так, что учащиеся постигают его в ходе решения конкретных задач, а затем происходит обобщение изученных примеров. Сначала рассматриваются уравнения с двумя переменными, линейные или нелинейные, затем неравенства и, наконец, системы уравнений и неравенств. Изучением этой темы подводится итог известным учащимся методам решения уравнений и неравенств. Рассмариваются методы, с которыми они ранее знакомы не были, но знания, которые приходится применять, хорошо известны и предстают с новой для учащихся стороны.
Тематическое планирование материала
| Глава | Тема | Часы | В том числе |
| Самостоятельные работы | контрольные работы |
|
| Повторение курса алгебры 10 класса | 3 | - | 1 |
| 1 | Тригонометрические функции | 19 | 3 | 1 |
| 2 | Производная и ее геометрический смысл | 22 | 5 | 1 |
| 3 | Применение производной к исследованию функций | 16 | 3 | 1 |
| 4 | Первообразная и интеграл | 15 | 5 | 1 |
| 5 | Комбинаторика | 10 | 2 | 1 |
| 6 | Элементы теории вероятностей | 11 | 1 | 1 |
| 7 | Комплексные числа | 14 | 4 | 1 |
|
| Итоговое повторение курса алгебры и начал анализа | 26 | - | 1 |
Календарно-тематическое планирование
| № урока | № в теме | Тема | Виды деятельности учащихся
(на уровне учебных действий) | Сроки изучения | Вид контроля |
| план | факт |
|
| Повторение курса алгебры и начал математического анализа 10 класса (3ч) |
-
| 1 | Тригонометрические формулы, уравнения | Решать упражнения на вычисления значений и упрощение тригонометрических выражений |
|
| Ответы у доски |
-
| 2 | Логарифмические, показательные уравнения и неравенства | Решать уравнения и неравенства перечисленных типов |
|
| Проверка д/з, ответы у доски, обучающая с/р |
-
| 3 | Входная контрольная работа | Решение заданий контрольной работы |
|
|
|
|
Глава I. Тригонометрические функции (19ч)
|
-
| 1 | Область определения и множество значений тригонометрических функций | Актуализировать знания о понятии функции, области определения, множестве значения функции С помощью единичной окружности определить область определения и множество значений функций 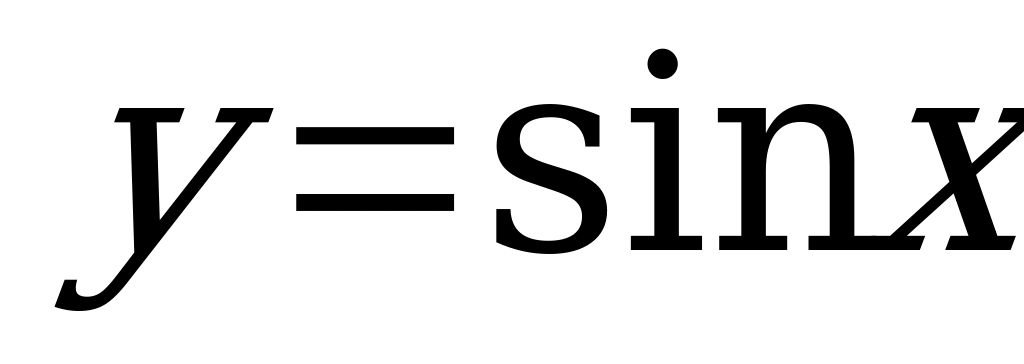 , , 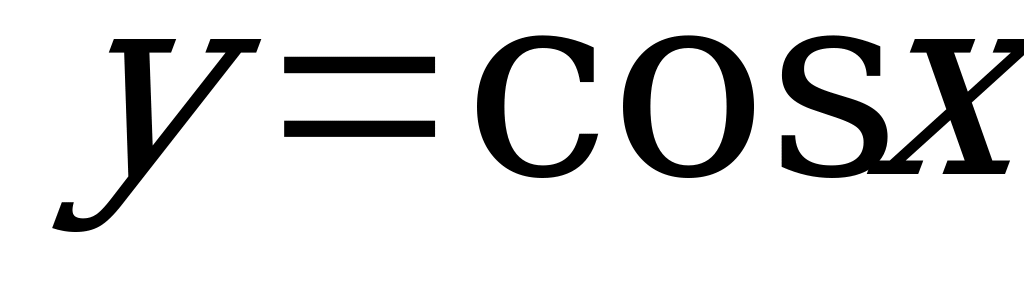 , ,  , , 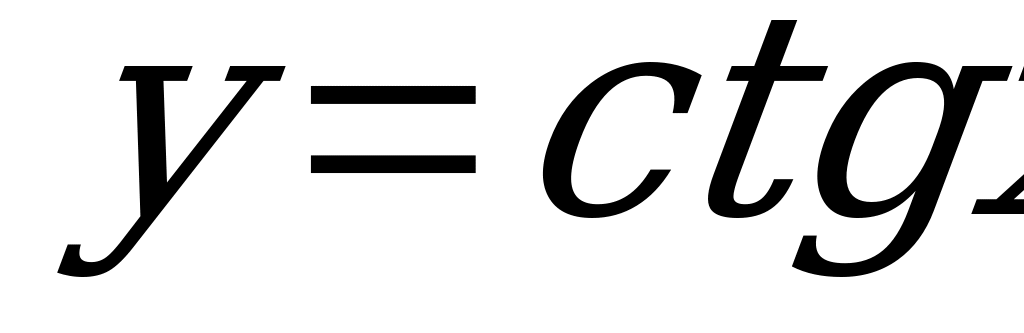 Решать задачи на нахождение области определение функции сложного аргумента, представленного в виде дроби или корня, множества значений функции вида  , , 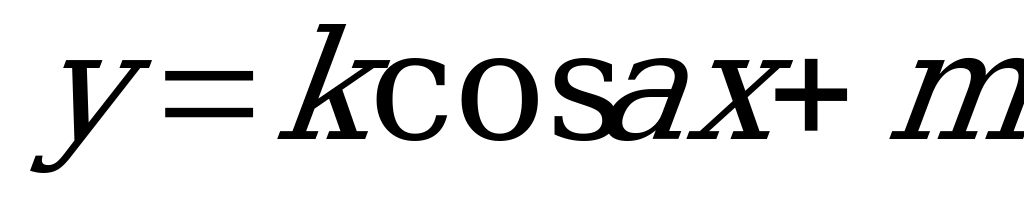 |
|
| Проверка д/з, ответы у доски, обучающая с/р |
-
| 2 | Множество значений тригонометрических функций | Решать задачи на нахождение области определения тригонометрических функций Решать задачи на нахождение множества значений тригонометрических функций вида  , ,  , ,  |
|
|
-
| 3 | Чётность, нечётность тригонометрических функций | Формулировать определения и свойства чётных и нечётных функций Формулировать свойства чётности и нечётности тригонометрических функций Решать задачи на определение чётности и нечётности функций |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
-
| 4 | Периодичность тригонометрических функций | Формулировать определение периодических функций Формулировать свойства периодичности тригонометрических функций Решать задачи на доказательство периодичности функций и нахождение наименьшего положительного периода тригонометрических функций |
|
|
-
| 5 | Самостоятельная работа на тему: «Чётность, нечётность, периодичность тригонометрических функций» | Решать задачи на определение чётности, нечётности и периодичности функций |
|
| С/р |
-
| 6 | Функция  ее свойства и график ее свойства и график | Формулировать свойства функции  строить её график строить её график Решать задачи на определение свойств функции  с применением графика с применением графика |
|
| Проверка д/з, ответы у доски, обучающая с/р |
-
| 7 | Функция 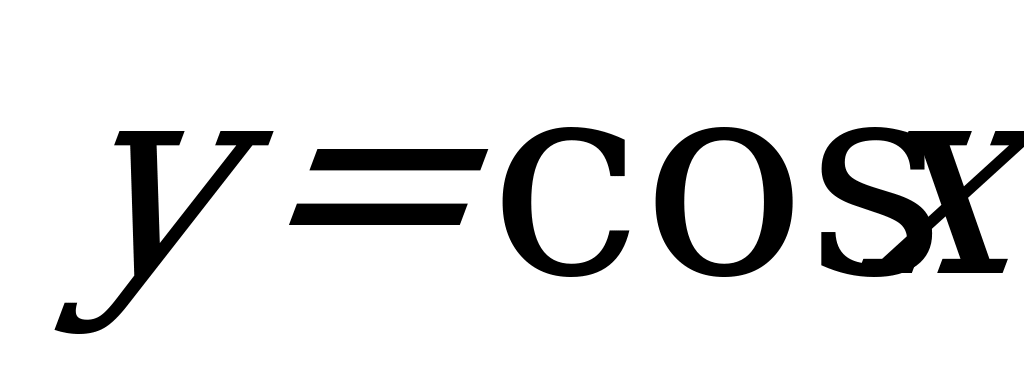 . Графическое решение тригонометрических уравнений и неравенств . Графическое решение тригонометрических уравнений и неравенств | Решать тригонометрические уравнения и неравенства на промежутке с применением графика функции 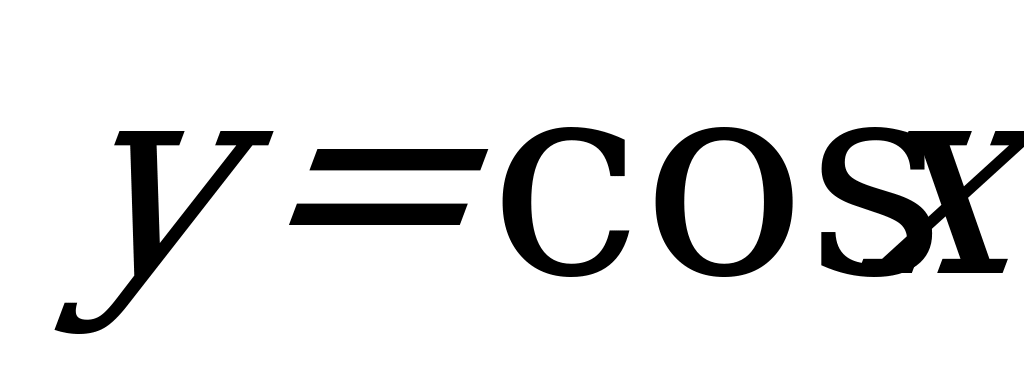 . . |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
-
| 8 | Функция  ее свойства и график ее свойства и график | Решать задания на применение свойств функции 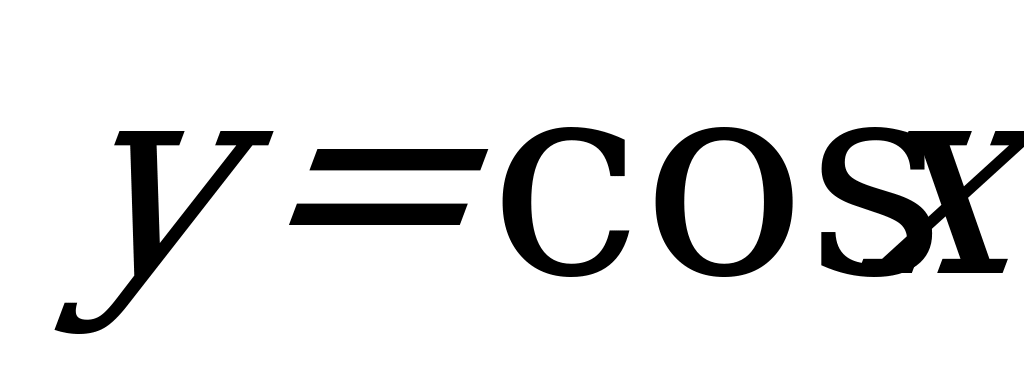 . . |
|
|
-
| 9 | Функция 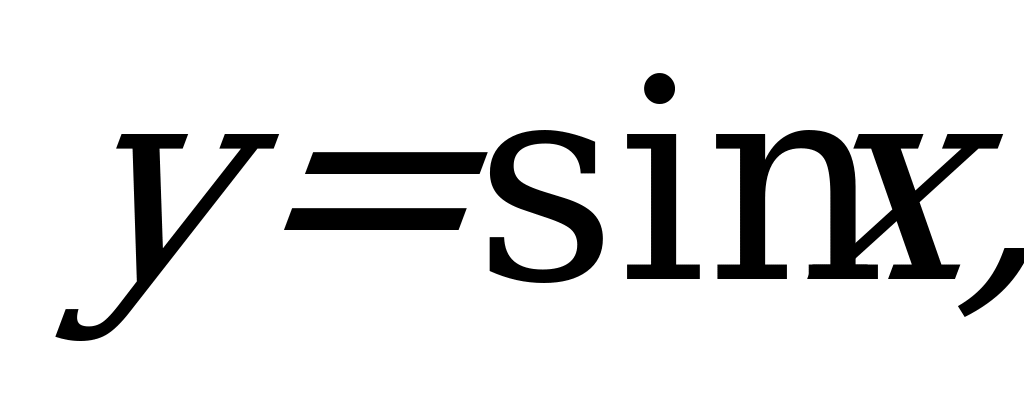 ее свойства и график ее свойства и график | Формулировать свойства функции 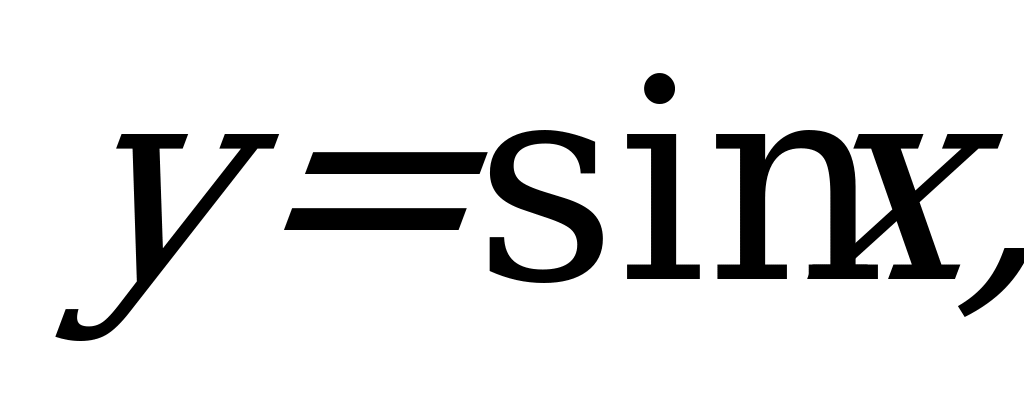 строить её график строить её график Решать задачи на определение свойств функции 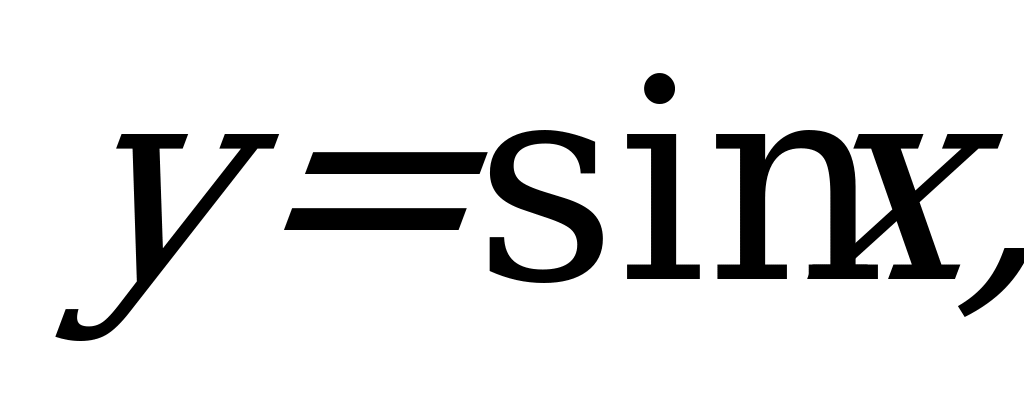 с применением графика с применением графика |
|
| Проверка д/з, ответы у доски, обучающая с/р |
-
| 10 | Функция  . Графическое решение тригонометрических уравнений и неравенств . Графическое решение тригонометрических уравнений и неравенств | Решать тригонометрические уравнения и неравенства на промежутке с применением графика функции  . . |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
-
| 11 | Функция 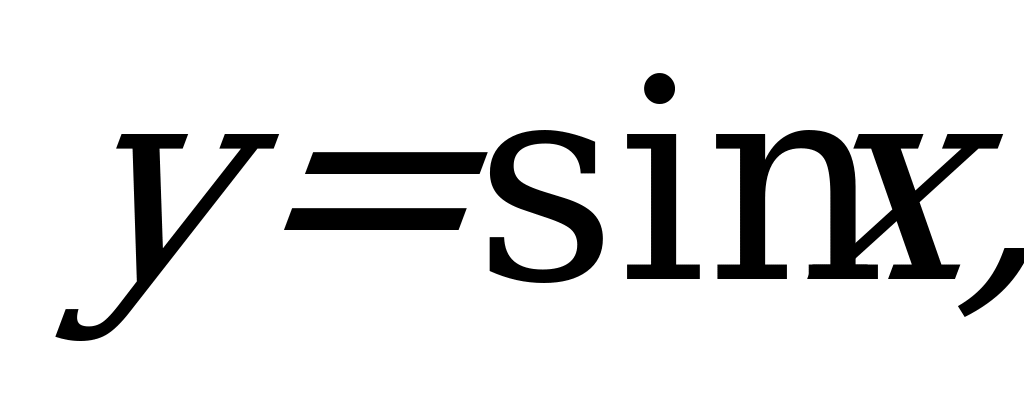 ее свойства и график ее свойства и график | Решать задания на применение свойств функции  . . |
|
| С/р |
-
| 12 | Функции 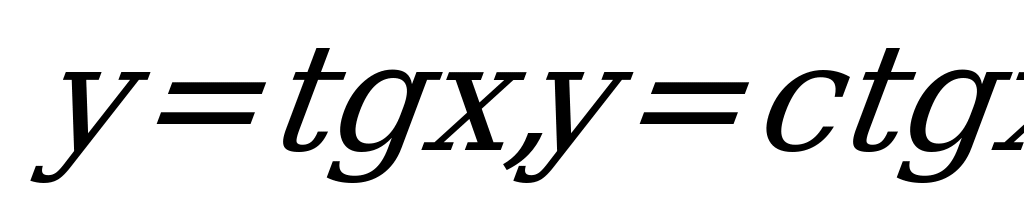 их свойства и графики их свойства и графики | Формулировать свойства функций 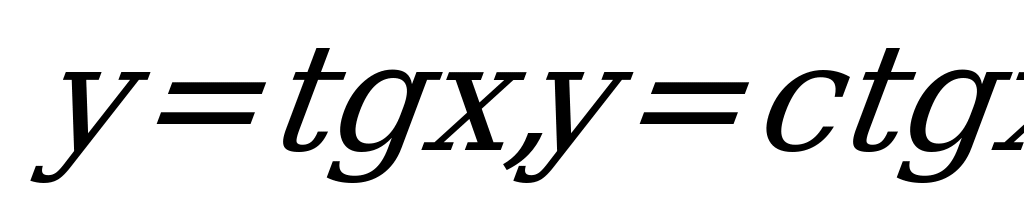 строить их графики строить их графики Решать задачи на определение свойств функции 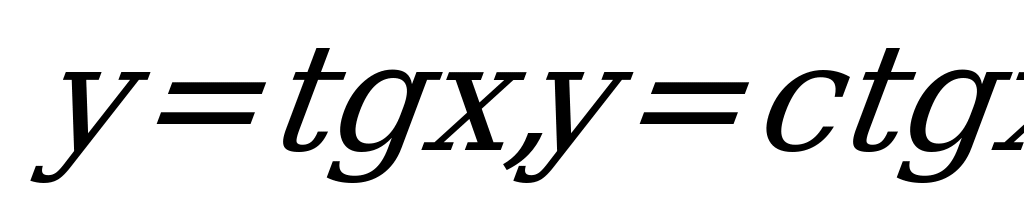 с применением графика с применением графика |
|
| Проверка д/з, ответы у доски, обучающая с/р |
-
| 13 | Функции 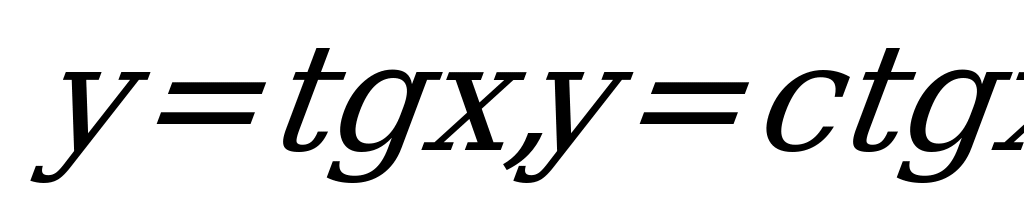 . Графическое решение тригонометрических уравнений и неравенств . Графическое решение тригонометрических уравнений и неравенств | Решать задания на применение свойств функции 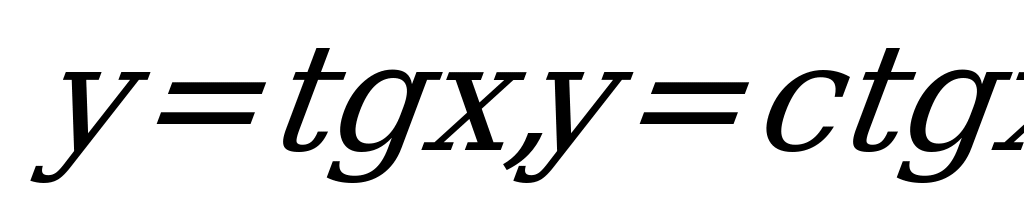 . . |
|
| С/р |
-
| 14 | Обратные тригонометрические функции | Формулировать определение и свойства обратных тригонометрических функций Решать задачи на применение свойств обратных тригонометрических функций Преобразовывать выражения, содержащие обратные тригонометрические функции |
|
| Проверка д/з, ответы у доски, обучающая с/р |
-
| 15 | Решение уравнений и неравенств, содержащих обратные тригонометрические функции | Решать уравнения и неравенства на применение свойств обратных тригонометрических функций Доказывать тождества, содержащие обратные тригонометрические функции |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
-
| 16 | Обратные тригонометрические функции | Решать задачи на применение свойств обратных тригонометрических функций |
|
| Проверка д/з, ответы у доски, обучающая с/р |
-
| 17 | Урок обобщения и систематизации знаний по теме «Тригонометрические функции» | Решать задания на применение свойств тригонометрических функций |
|
| Проверка д/з, ответы у доски |
-
| 18 | Урок обобщения и систематизации знаний по теме «Тригонометрические функции» |
|
|
-
| 19 | Контрольная работа №1 по теме «Тригонометрические функции» | Оформлять решение. Выполнять задания по заданному алгоритму |
|
| К/р |
|
Глава II. Производная и её геометрический смысл (22ч)
|
-
| 1 | Предел последовательности (определение и свойства) | Актуализировать знания о числовой последовательности Объяснять и иллюстрировать понятие, формулировать определение предела числовой последовательности, свойства сходящихся последовательностей, теоремы о пределе монотонной последовательности Решать задачи на доказательство того, что предел заданной последовательности равен данному числу |
|
| Ответы у доски, обучающая с/р |
| 24,25 | 2,3 | Вычисление пределов последовательностей | Использовать определение предела последовательности, теоремы о пределе монотонной последовательности, а также связанные с арифметическими действиями над последовательностями для вычисления пределов последовательностей |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
| 26,27 | 4,5 | Предел функции (определение, свойства). Вычисление пределов функций.
| Объяснять и иллюстрировать понятие и формулировать определение и свойства предела функции в точке и на бесконечности, пределов функции справа и слева, бесконечно малых функций; определение функции, непрерывной в точке, на интервале и отрезке, свойства функций, непрерывных на отрезке, теорему о промежуточных значениях Формулировать свойства предела функции Определять по графику значение предела функции, с помощью графика, является ли функция непрерывной на всей числовой прямой или на каких промежутках Находить асимптоты графиков функций Вычислять пределы функций |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски |
| 28. | 6 | Непрерывность функции
| Формулировать определение непрерывной функции Определять с помощью графика, является ли функция непрерывной на всей числовой прямой или на каких промежутках Вычислять пределы функций |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
| 29. | 7 | Определение производной | Формулировать определения мгновенной скорости, производной Вычислять производные функций по определению производной, находить производные функций  , , 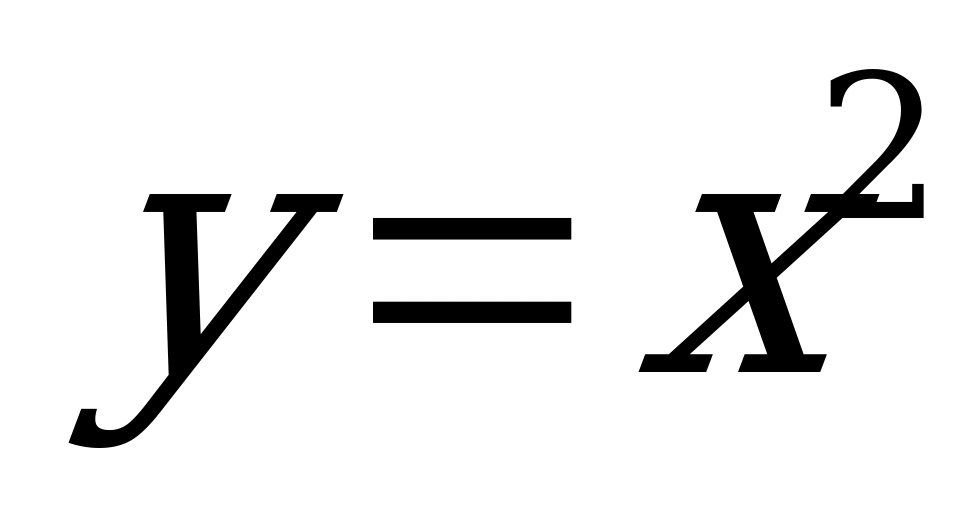 , , 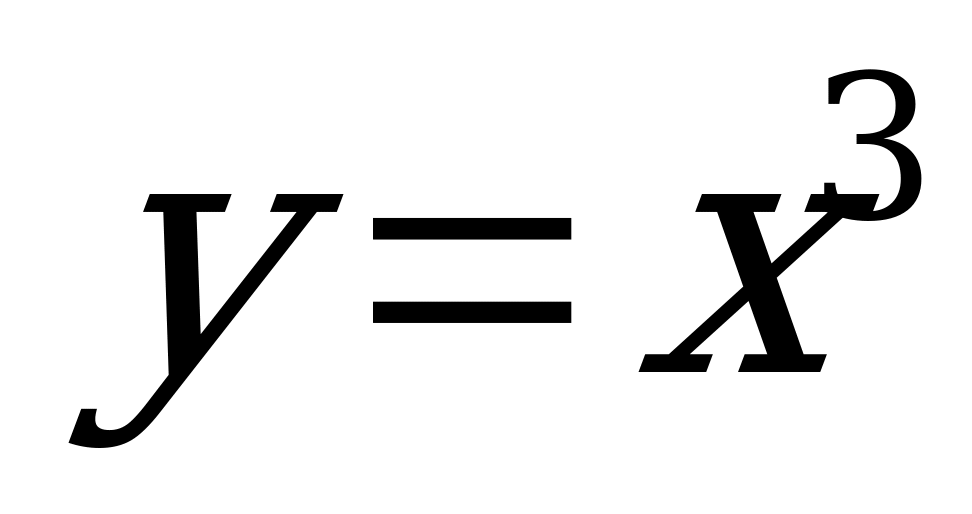 |
|
| Проверка д/з, ответы у доски, обучающая с/р |
| 30. | 8 | Вычисление производной функции по определению | Решать задачи на вычисление производной, используя определением производной |
|
| С/р |
| 31. | 9 | Дифференцирование суммы, произведения и частного | Формулировать правила дифференцирования суммы, произведения и частного Применять изученный материал для нахождения производных функций, решать уравнения вида 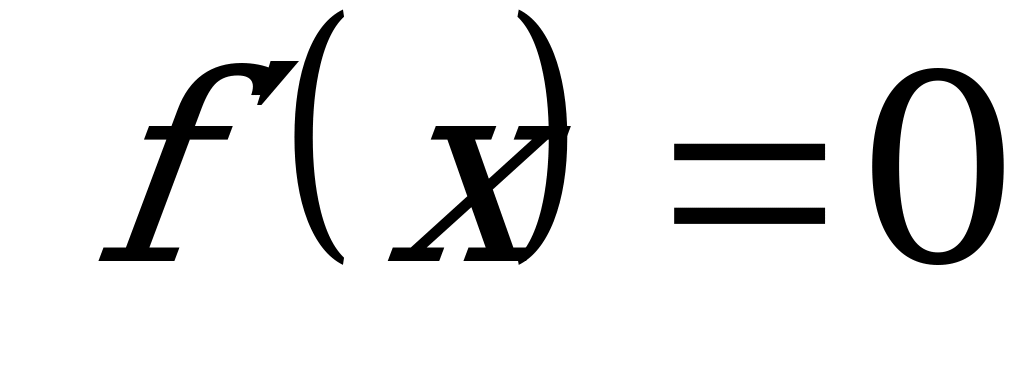 , неравенства вида , неравенства вида  , ,  |
|
| Проверка д/з, ответы у доски, обучающая с/р |
| 32. | 10 | Дифференцирование сложной и обратной функции | Формулировать правила дифференцирования сложной и обратной функций Применять изученный материал для решения задач, связанных с производной |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
| 33. | 11 | Правила дифференцирования | Применять изученные правила дифференцирования для решения задач, связанных с производной |
|
| С/р |
| 34. | 12 | Производная степенной функции | Формулировать правило дифференцирования степенной функции Применять изученный материал для нахождения производных функций, решать уравнения вида 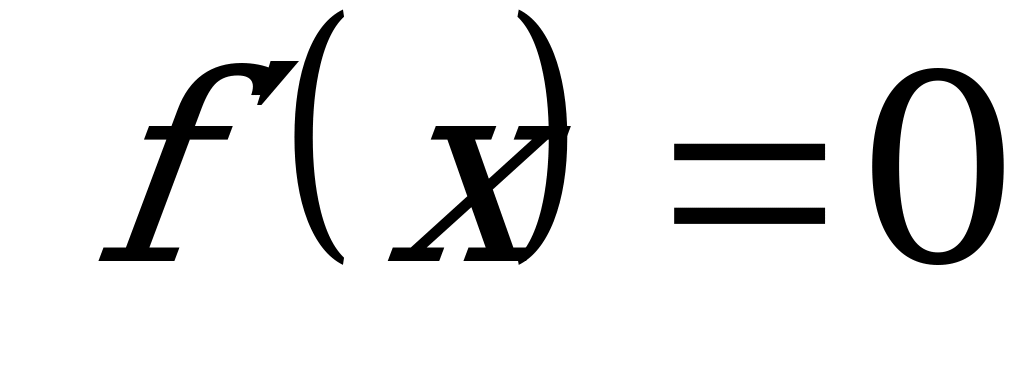 , неравенства вида , неравенства вида  , ,  |
|
| Проверка д/з, ответы у доски, обучающая с/р |
| 35. | 13 | Производная степенной функции | Применять правила дифференцирования и формулу производной степенной функции для решения задач, связанных с производной |
|
| С/р |
| 36. | 14 | Производные некоторых элементарных функций | Формулировать правила дифференцирования тригонометрических, показательной, логарифмической функций Применять изученные формулы для нахождения производных |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
| 37. | 15 | Решение задач на нахождение производных элементарных функций | Выводить формулы дифференцирования обратных тригонометрических функций Применять изученные формулы для нахождения производных функций, решать уравнения вида 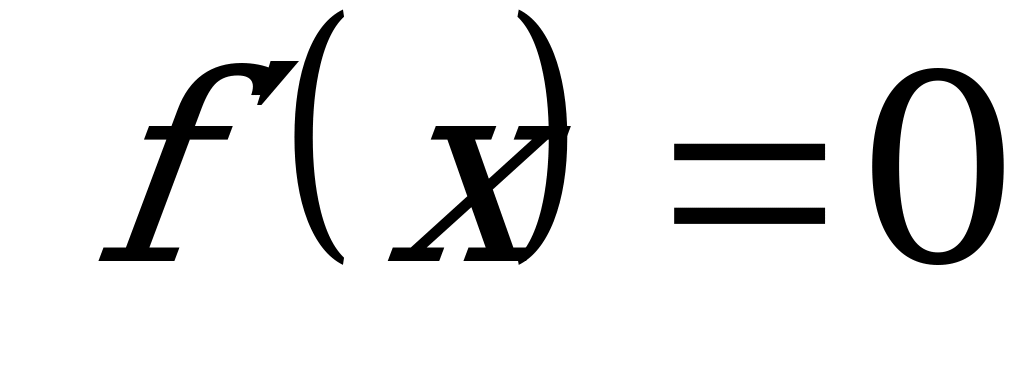 , неравенства вида , неравенства вида  , ,  |
|
|
| 38. | 16 | Производные некоторых элементарных функций | Применять изученные формулы для решения задач, связанных с производной |
|
| С/р |
| 39. | 17 | Геометрический смысл производной | Иллюстрировать, объяснять и формулировать понятие углового коэффициента прямой, касательной к графику функции, геометрический смысл производной Решать задачи на написание уравнения прямой, с заданным угловым коэффициентом и проходящим через данную точку Решать задачи, связанные с геометрическим смыслом производной |
|
| Проверка д/з, ответы у доски, обучающая с/р |
| 40. | 18 | Уравнение касательной к графику функции | Вывести уравнение касательной к графику функции в данной точке Решать задачи на написание уравнения касательной к графику функции |
|
|
| 41. | 19 | Геометрический смысл производной | Решать задачи на написание уравнения касательной к графику функции, а также связанные с геометрическим смыслом производной |
|
| С/р |
| 42,43 | 20,21 | Урок обобщения и систематизации знаний по теме «Производная и ее геометрический смысл» | Решать задачи на нахождение производных функций, а также связанных с геометрическим смыслом производной |
|
| Проверка д/з, фронтальный оп рос теории, ответы у доски, обучающая с/р |
| 44. | 22 | Контрольная работа №2 по теме «Производная и ее геометрический смысл» | Оформлять решение. Выполнять задания по заданному алгоритму |
|
| К/р |
|
Глава III. Применение производной к исследованию функций (16ч)
|
| 45. | 1 | Возрастание и убывание функции | Иллюстрировать и формулировать теорему Лагранжа Формулировать определение критической и стационарной точек функции Формулировать и доказывать достаточные условия монотонности функции Решать задачи на нахождение промежутков монотонности любой комбинации элементарных функций |
|
| Проверка д/з, ответы у доски, обучающая с/р |
| 46. | 2 | Возрастание и убывание функции. Решение задач | Решать задачи на нахождение промежутков монотонности функции |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
| 47. | 3 | Экстремумы функции | Иллюстрировать понятие и формулировать определение экстремумов функции Иллюстрировать и объяснять суть теоремы Ферма Формулировать и доказывать достаточные условия экстремумов Решать задачи на нахождение экстремумов функции |
|
| Проверка д/з, ответы у доски, обучающая с/р |
| 48. | 4 | Экстремумы функции. Решение задач | Решать задачи на нахождение экстремумов функции |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
| 49. | 5 | Возрастание и убывание и экстремумы функции | Решать задачи на нахождение промежутков монотонности и экстремумов функции |
|
| С/р |
| 50. | 6 | Наибольшее и наименьшее значения функции, непрерывной на отрезке (изучение алгоритма) | Формулировать алгоритм нахождения наибольшего (наименьшего) значений функции, непрерывной на отрезке, а также на интервале, содержащем только одну критическую точку Решать задачи на нахождения наибольшего (наименьшего) значения функции, непрерывной на отрезке, а также на интервале, содержащем только одну критическую точку |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
| 51. | 7 | Задачи на нахождение наибольшего (наименьшего) значения величин | Формулировать алгоритм решения задач на нахождение наибольшего (наименьшего) значения величины Решать задачи на нахождение наибольшего (наименьшего) значения величины, используя изученный алгоритм |
|
|
|
| 52. | 8 | Наибольшее и наименьшее значения функции | Решать задачи на нахождения наибольшего (наименьшего) значения функции |
|
| С/р |
| 53. | 9 | Производная второго порядка, выпуклость и точки перегиба | Объяснять понятие производной второго порядка Формулировать определение функции, выпуклой вверх (вниз), точки перегиба, а также достаточные условия выпуклости функции Решать задачи на нахождение промежутков выпуклости функции и точек перегиба |
|
| Проверка д/з, ответы у доски, обучающая с/р |
| 54. | 10 | Асимптоты графиков функций | Иллюстрировать, объяснять и формулировать понятия вертикальной, горизонтальной и наклонной асимптот к графику функции Формулировать и доказывать необходимое и достаточное условие асимптоты Решать задачи на нахождение асимптоты к графику функции |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
| 55. | 11 | Применение производной к построению графиков функций (изучение алгоритма) | Формулировать алгоритм построения графика функции с помощью производной Выполнять построение графиков функций с помощью производной по изученному алгоритму |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
| 56. | 12 | Построение графиков функции и помощью производной, содержащих асимптоты | Выполнять построение графиков функций с помощью производной |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
| 57. | 13 | Применение производной к построению графиков функций, содержащих асимптоты |
|
|
| 58. | 14 | Применение производной к построению графиков функций |
|
|
| 59. | 15 | Урок обобщения и систематизации знаний по теме «Применение производной к исследованию функции» | Решать задачи на нахождение промежутков монотонности функции, экстремумов функции, наибольшего (наименьшего) значения функции с помощью производной
Выполнять построение графиков функций с помощью производной |
|
| С/р |
| 60. | 16 | Контрольная работа №3по теме «Применение производной к исследованию функции» | Оформлять решение. Выполнять задания по заданному алгоритму |
|
| К/р |
|
Глава IV. Первообразная и интеграл – 15 часов
|
| 61.
| 1 | Первообразная | Формулировать определение первообразной функции Составить таблицу первообразных некоторых функций Решать задачи на применение понятия первообразной и нахождение первообразных функций |
|
| Ответы у доски, обучающая с/р |
| 62. | 2 | Первообразная. Решение задач | Решать задачи на применение понятия первообразной и нахождение первообразных функций |
|
| С/р |
| 63. | 3 | Правила нахождения первообразных | Формулировать правила нахождения первообразных Дополнить таблицу первообразных, составленную на уроке 59 Решать задачи на нахождение первообразных функций |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
| 64. | 4 | Правила нахождения первообразных | Решать задачи на нахождение первообразных функций |
|
| С/р |
| 65. | 5 | Площадь криволинейной трапеции и интеграл. | Формулировать понятие криволинейной трапеции, определённого интеграла Записывать формулу Ньютона-Лейбница Изображать криволинейную трапецию Вычислять площади криволинейных трапеций |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
| 66.
| 6 | Вычисление интегралов. | Вычислять интегралы по Формуле Ньютона-Лейбница |
|
|
| 67. | 7 | Площадь криволинейной трапеции и интеграл Вычисление интегралов. | Вычислять площади криволинейных трапеций и интегралы по Формуле Ньютона-Лейбница |
|
| С/р |
| 68. | 8 | Вычисление площадей с помощью интегралов | Формулировать алгоритмы различных вариантов вычисления площадей с помощью интегралов Вычислять площади фигур, ограниченных графиками функций, с помощью определённого интеграла |
|
| Проверка д/з, ответы у доски, обучающая с/р |
| 69. | 9 | Вычисление площадей с помощью интегралов | Формулировать алгоритмы различных вариантов вычисления площадей с помощью интегралов Вычислять площади фигур, ограниченных графиками функций, с помощью определённого интеграла |
|
| Проверка д/з, ответы у доски, обучающая с/р |
| 70. | 10 | Вычисление площадей с помощью интегралов | Формулировать алгоритмы различных вариантов вычисления площадей с помощью интегралов Вычислять площади фигур, ограниченных графиками функций, с помощью определённого интеграла |
|
| С/р |
| 71. | 11 | Применение интегралов для решения физических задач | Вычислять площади фигур, ограниченных графиками функций, с помощью определённого интеграла Решать задачи на применение интеграла в физике |
|
| Проверка д/з, ответы у доски, обучающая с/р |
| 72. | 12 | Простейшие дифференциальные уравнения | Решать простейшие дифференциальные уравнения |
|
|
| 73. | 13 | Урок обобщения и систематизации знаний по теме «Интеграл» | Решать задачи на вычисление первообразных функции, определённых интегралов, площадей с помощью интеграла |
|
| С/р |
| 74. | 14 | Урок обобщения и систематизации знаний по теме «Интеграл» |
|
| Проверка д/з, ответы у доски |
| 75. | 15 | Контрольная работа №4 по теме «Интеграл» | Оформлять решение. Выполнять задания по заданному алгоритму |
|
| К/р |
|
Глава V. Комбинаторика (13ч)
|
| 76,77. | 1,2 | Математическая индукция |
|
|
|
|
| 78,79.
| 3,4 | Правило произведения. Размещения с повторениями | Формулируют правило произведения Знакомиться с понятием определение размещения с повторениями Решать комбинаторные задачи на подсчёт числа вариантов с помощью правила произведения |
|
| Ответы у доски, обучающая с/р |
| 80 | 5 | Перестановки | Знакомятся с понятием перестановки, формулой числа перестановок n элементов, а также перестановок n элементов с повторениями Решать задачи на применение изученных формул Создавать математические модели для решения комбинаторных задач, сводимых к подсчету числа перестановок |
|
| Проверка д/з, ответы у доски, обучающая с/р |
| 81 | 6 | Перестановки | Решать задачи на применение правила произведения, перестановок, а также перестановок с повторениями Создавать математические модели для решения комбинаторных задач, сводимых к подсчету числа перестановок |
|
| С/р |
| 82. | 7 | Размещения без повторений | Знакомиться с понятием размещения без повторений Создавать математические модели для решения комбинаторных задач, сводимых к подсчету числа размещений |
|
| Проверка д/з, ответы у доски, обучающая с/р |
| 83. | 8 | Сочетания без повторений и бином Ньютона | Знакомиться с сочетаниями и их свойствами Создавать математические модели для решения комбинаторных задач, сводимых к подсчету числа сочетаний без повторений |
|
|
| 84. | 9 | Сочетания без повторений и бином Ньютона | Знакомиться с сочетаниями и их свойствами Создавать математические модели для решения комбинаторных задач, сводимых к подсчету числа сочетаний без повторений |
|
|
| 85. | 10 | Сочетания без повторений и бином Ньютона | Создавать математические модели для решения комбинаторных задач, сводимых к подсчету числа сочетаний без повторений |
|
| С/р |
| 86. | 11 | Сочетания с повторениями |
|
|
|
|
| 87. | 12 | Урок обобщения и систематизации знаний по теме «Комбинаторика» | Решать комбинаторные задачи различных типов |
|
| Проверка д/з, ответы у доски, обучающая с/р |
| 88. | 13 | Контрольная работа №5 по теме «Комбинаторика» | Оформлять решение. Выполнять задания по заданному алгоритму |
|
| К/р |
|
Глава VI. Элементы теории вероятностей (11ч)
|
| 89,90. | 1,2 | Вероятность события | Актуализовать знания о типах событий, вероятности события Решать задачи на нахождение вероятности событий |
|
| Ответы у доски, обучающая с/р |
| 91. | 3 | Сложение вероятностей | Знакомиться с теоремой о сумме вероятностей двух несовместных событий, а также о сумме вероятностей двух произвольных событий Применять изученные теоремы при решении задач |
|
| Проверка д/з, ответы у доски, обучающая с/р |
| 92. | 4 | Сложение вероятностей | Применять теоремы о сумме вероятностей при решении задач |
|
| С/р |
| 93. | 5 | Условная вероятность. Независимость событий | Формулировать определения независимых событий, условной вероятности Вычислять условную вероятность для характеристики одних события от других |
|
| Проверка д/з, ответы у доски |
| 94,95,96. | 6,7,8 | Вероятность произведения независимых событий | Решать задачи на вычисление вероятности совместного появления независимых событий, вероятности произведения независимых событий или событий, независимых в совокупности |
|
|
| 97. | 9 | Формула Бернулли | Знакомиться с формулой Бернулли Вычислять вероятность события B, заключающегося в том, что при n испытаниях событие A произойдёт ровно k раз |
|
| Проверка д/з, ответы у доски |
| 98. | 10 | Урок обобщения и систематизации знаний по теме «Элементы теории вероятности» | Вычислять вероятность события, используя материал главы VI. |
|
| Проверка д/з, ответы у доски |
| 99. | 11 | Контрольная работа №6 по теме «Элементы теории вероятности» | Оформлять решение. Выполнять задания по заданному алгоритму |
|
| К/р |
|
Глава VII. Комплексные числа (14ч)
|
| 100. | 1 | Определение комплексных чисел. Сложение и умножение комплексных чисел. | Знакомиться с понятием комплексных чисел Определять действительную и мнимую части комплексного числа; Выполнять действия сложения и умножения комплексного числа, заданного алгебраической формой |
|
| Ответы у доски |
| 101. | 2 | Определение комплексных чисел. Сложение и умножение комплексных чисел. |
|
| С/р |
| 102. | 3 | Комплексно сопряженные числа. Модуль комплексного числа. | Формулировать определение комплексно сопряжённых чисел, противоположных чисел Вычислять модуль комплексного числа, заданного алгебраической формой Выполнять действия вычитания и деления комплексного числа, заданного алгебраической формой |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
| 103. | 4 | Вычитание и деления комплексных чисел | Выполнять действия вычитания и деления комплексного числа, заданного алгебраической формой |
|
| С/р |
| 104. | 5 | Геометрическая интерпретация комплексного числа. | Знакомиться с геометрической интерпретацией комплексного числа, геометрическим смыслом модуля комплексного числа и модуля разности двух комплексных чисел Находить множество точек плоскости, удовлетворяющих заданному условию |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
|
105, 106. | 6,7 | Геометрическая интерпретация комплексного числа. | Находить множество точек плоскости, удовлетворяющих заданному условию |
|
| С/р |
| 107. | 8 | Тригонометрическая форма комплексного числа | Формулировать определение аргумента комплексного числа Вычислять аргумент комплексного числа Записывать комплексные числа в тригонометрической форме |
|
| Проверка д/з, фронтальный опрос теории, ответы у доски, обучающая с/р |
| 108. | 9 | Умножение и деление комплексного числа, записанного в тригонометрической форме. Формула Муавра. | Выполнять умножение и деление комплексных чисел, записанных в тригонометрической форме Использовать формулу Муавра для возведение в степень комплексных чисел, записанных в тригонометрической форме |
|
|
| 109. | 10 | Умножение и деление комплексного числа, записанного в тригонометрической форме. Формула Муавра. | Выполнять умножение и деление комплексных чисел, записанных в тригонометрической форме Использовать формулу Муавра для возведение в степень комплексных чисел, записанных в тригонометрической форме |
|
|
| 110. | 11 | Квадратное уравнение с комплексной переменной | Решать квадратное уравнение с комплексным неизвестным, а также уравнения сводящиеся к квадратным
|
|
|
| 111. | 12 | Извлечение корня из комплексного числа. Алгебраические уравнения | Вычислять корень из любого числа, используя тригонометрическую запись комплексного числа |
|
| С/р |
| 112. | 13 | Урок обобщения и систематизации знаний по теме «Комплексные числа» | Выполнять действия над комплексными числами, записанными в различной форме Находить характеристики комплексных чисел Изображать числа на комплексной плоскости Решать квадратные уравнения с комплексными неизвестными |
|
| Ответы у доски, обучающая с/р |
| 113. | 14 | Контрольная работа №7 по теме «Комплексные числа» | Оформлять решение. Выполнять задания по заданному алгоритму |
|
| К/р |
| Итоговое повторение курса алгебры и начал математического анализа (23ч)
|
|
114, 115. | 1,2 | Степени и корни | Выполнять арифметические действия, сочетая устные и письменные приемы Находить значения корня натуральной степени по известным формулам и правилам преобразования буквенных выражений, включающих радикалы |
|
| Проверка д/з, ответы у доски, обучающая с/р |
|
116,117. | 3,4 | Преобразование логарифмических выражений | Находить значения логарифмических выражений, используя определение и свойства логарифмов Выполнять преобразования логарифмических выражений, используя определение и свойства логарифмов |
|
| Проверка д/з, ответы у доски |
|
118,119. | 5,6 | Преобразование тригонометрических выражений | Находить значения тригонометрических выражений Выполнять преобразования тригонометрических выражений |
|
| Проверка д/з, ответы у доски |
| 120,121. | 7,8 | Решение тригонометрических уравнений, сводящихся к квадратным, однородных, линейных относительно  и и  | Решать тригонометрические уравнения сводящиеся к квадратным, однородные, линейные относительно  и и  |
|
| Проверка д/з, ответы у доски |
|
122,123. | 9,10 | Решение иррациональных уравнений | Решать иррациональных уравнения различных типов |
|
|
|
|
124,125. | 11,12 | Уравнение касательной к графику функции. Применение производной для исследования функций | Решать задания на нахождения наибольшего (наименьшего) значения функции (B-13) Решать задания на применение производной для определение характера монотонности и экстремумов функции (B-8) |
|
| Проверка д/з, ответы у доски |
|
126,127. | 13,14 | Первообразная | Находить значения первообразных функции Решать задания B-8, связанные с первообразной |
|
| Проверка д/з, ответы у доски |
|
128,129. | 15,16 | Интеграл | Находить значения определённого интеграла по формуле Ньютона-Лейбница Находить площадь криволинейной трапеции Находить площади фигур, ограниченных линиями, с помощью определённого интеграла |
|
|
Проверка д/з, ответы у доски |
|
130,131. | 17,18 | Повторение. Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке. | Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке. |
|
|
| 132. | 19 | Повторение. Текстовые задачи. | Решение текстовых задач |
|
|
| 133,134. | 20,21 | Решение текстовых задач |
|
|
| Проверка д/з, ответы у доски |
| 135 | 23 | Итоговая контрольная работа за курс средней (полной школы) | Решать тестовые задания с краткой формой записи ответа и подробным решением по материалам ЕГЭ |
|
| К/Р |
| 136 | 24 | Подведение итогов |
|
|
|
|
Учебно-методическое обеспечение предмета Основное
Для учащихся:
-
Ю.М. Колягин, М.В.Ткачева, Н.Е.Федорова, М.И.Шабунин. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и углубленный уровни. — М.: Просвещение, 2014г..
Для учителя:
-
Федорова Н.Е. Изучение алгебры и начал математического анализа в 11 классе: кн. для учителя/ Н.Е.Федорова, М.В.Ткачева. — М.: Просвещение, 2009.
-
Шабунин М.И., Ткачева М.В., Федорова Н.Е., Доброва О.Н. Алгебра и начала математического анализа: дидакт. материалы для 11 кл. общеобразоват. учреждений: профил. уровень, — М.: Просвещение, 2009.
-
Шабунин М.И., Ткачева М.В., Федорова Н.Е., Газарян Р.Г. Дидактические материалы по алгебре и началам анализа для 11 классов общеобразовательных учреждений, — 3-е изд. — М.: Просвещение, 2009.
Дополнительное
Для учащихся:
-
ЕГЭ 2014. Математика. 30 вариантов типовых тестовых заданий и 800 заданий части 2(C) / И.Р. Высоцкий, П.И. Захаров, B.C. Панферов, С.Е. Посицельский, А.В. Семенов, A.Л. Семенов, М.А. Семенова, И.Н. Сергеев, В.А. Смирнов, С.А. Шестаков, Д.Э. Шноль, И.В. Ященко; под ред. A.JI. Семенова, И.В. Ященко. — М.: Издательство «Экзамен», 2014. — 215, [1] с. (Серия «ЕГЭ. 30 вариантов. Типовые тестовые задания»)
-
ЕГЭ 2014. Математика. Типовые тестовые задания / И.Р. Высоцкий, П.И. Захаров, B.C. Панферов, С.Е. Посицельский, А.В. Семенов, М.А. Семенова, И.Н. Сергеев, В.А. Смирнов, С.А. Шестаков, Д.Э. Шноль, И.В. Ященко; под ред. А.Л. Семенова, И.В. Ященко. — М.: Издательство «Экзамен», 2014. — 95, [1] с. (Серия «ЕГЭ. ТРК. Типовые тестовые задания»)
-
ЕГЭ-2014. Математика : типовые экзаменационные варианты : 30 вариантов / под ред. А. Л. Семенова, И. В. Ященко. — М.: Издательство «Национальное образование», 2013. — 192 с. — (ЕГЭ-2013. ФИПИ — школе).
Для учителя:
-
Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по алгебре и началам анализа для 10–11 классов. — М.: Илекса, 2008.
-
Зив Б.Г. Алгебра и начала анализа. 11 класс. Тесты. — СПб.: СМО Пресс, 2004.
-
Зив Б.Г., Гольдич В.А. Дидактические материалы по алгебре и началам анализа — СПб.: СМИО Пресс, 2008.
-
В. Шепелева. Алгебра и начала анализа. Тематические тесты. 11 класс. М., Просвещение, 2009.
Материально-техническое обеспечение предмета
1
10


























