ОБЛАСТНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«СМОЛЕНСКАЯ АКАДЕМИЯ ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ»
Сафоновский филиал областного государственного бюджетного
профессионального образовательного учреждения
«Смоленская академия профессионального образования»
(Сафоновский филиал ОГБПОУ СмолАПО)
Рабочая программа учебной дисциплины
ЕН.01 Математика
Для специальности 15.02.08 Технология машиностроения
(базовая подготовка)
2019 г.
| Рабочая программа учебной дисциплины разработана на основе Федерального государственного образовательного стандарта по специальности среднего профессионального образования 15.02.08 Технология машиностроения |
|
Разработчик: преподаватель Сафоновского филиала ОГБПОУ СмолАПО ____________Ю.А. Пшенова
| Рассмотрено
цикловой комиссией общеобразовательных дисциплин Сафоновского филиала ОГБПОУ СмолАПО (протокол от 29.08.2019г. №1) Председатель ______И.В. Кладко
| УТВЕРЖДЕНО методическим советом Сафоновского филиала ОГБПОУ СмолАПО (протокол от 29.08.2019г. №1) Председатель_______Г.Л. Полежаева |
|
|
|
|
|
|
|
| |
| |
СОДЕРЖАНИЕ
| | стр. |
| 1. Паспорт рабочей программы учебной дисциплины | 4 |
| 2. Перечень развиваемых компетенций | 5 |
| 3. Структура и содержание учебной дисциплины | 6 |
| 4. Условия реализации учебной дисциплины | 12 |
| 5. Контроль и оценка результатов освоения учебной дисциплины | 13 |
1 паспорт ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ
Математика
1.1 Область применения программы
Рабочая программа учебной дисциплины разработана на основе Федерального государственного образовательного стандарта (далее - ФГОС) по специальности среднего профессионального образования (далее – СПО) 15.02.08 Технология машиностроения (базовая подготовка).
Рабочая программа учебной дисциплины может быть использована в учреждениях среднего профессионального образования, реализующих основные образовательные программы СПО.
1.2 Место учебной дисциплины в структуре основной профессиональной образовательной программы:
Дисциплина «Математика» по специальности 15.02.08 Технология машиностроения является дисциплиной математического и общего естественнонаучного цикла.
Дисциплина «Математика» обеспечивается следующими дисциплинами общеобразовательного цикла «Математика», «Информатика и ИКТ».
1.3 Цели и задачи дисциплины – требования к результатам освоения учебной дисциплины:
В результате освоения дисциплины обучающийся должен уметь:
анализировать сложные функции и строить их графики;
выполнять действия над комплексными числами;
вычислять значения геометрических величин;
производить операции над матрицами и определителями;
решать задачи на вычисление вероятности с использованием элементов комбинаторики;
решать прикладные задачи с использованием элементов дифференциального и интегрального исчислений;
решать системы линейных уравнений различными методами;
В результате освоения дисциплины обучающийся должен знать:
основные математические методы решения прикладных задач;
основные понятия и методы математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики;
основы интегрального и дифференциального исчисления;
роль и место математики в современном мире при освоении профессиональных дисциплин и в сфере профессиональной деятельности.
1.4 Количество часов на освоение программы учебной дисциплины:
максимальной учебной нагрузки обучающегося 120 часов, в том числе:
обязательной аудиторной учебной нагрузки обучающегося 80 часов;
самостоятельной работы обучающегося 40 часов.
2 ПЕРЕЧЕНЬ РАЗВИВАЕМЫХ КОМПЕТЕНЦИЙ
Дисциплина направлена на развитие следующих общих (ОК) и профессиональных (ПК) компетенций:
| Код | Наименование результата обучения |
| ОК 2. | Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество |
| ОК.4 | Осуществлять поиск, анализ и оценку информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития |
| ОК.5 | Использовать информационно-коммуникационные технологии для совершенствования профессиональной деятельности |
| ОК.8 | Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации |
| ПК. 1.4 | Разрабатывать и внедрять управляющие программы обработки деталей |
| ПК-1.5 | Использовать системы автоматизированного проектирования технологических процессов обработки деталей |
| ПК - 2.1. | Участвовать в планировании и организации работы структурного подразделения |
| ПК-3.2 | Проводить контроль соответствия качества деталей требованиям технической документации |
3 СТРУКТУРА И СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ 3.1 Объем учебной дисциплины и виды учебной работы
| Вид учебной работы | Объем часов |
| Максимальная учебная нагрузка (всего) | 120 |
| Обязательная аудиторная учебная нагрузка (всего) | 80 |
| в том числе: |
|
| лекционное занятие | 20 |
| семинарское занятие | 20 |
| лабораторные занятия | 0 |
| практические занятия | 40 |
| контрольные работы | 12 |
| курсовая работа (проект) (если предусмотрено) | 0 |
| Самостоятельная работа обучающегося (всего) | 40 |
| в том числе: |
|
| решение упражнений выполнение тестовых заданий составление опорных конспектов составление таблиц для систематизации учебного материала учебно-исследовательская работа | 20 6 4 4
6 |
| Итоговая аттестация в форме дифференцированного зачета |
3.2. Примерный тематический план и содержание учебной дисциплины «МАтематика»
| Наименование разделов и тем | Содержание учебного материала, лабораторные и практические работы, самостоятельная работа обучающихся | Объем часов | Уровень освоения |
| 1 | 2 | 3 | 4 |
| Раздел 1 Элементы аналитической геометрии и линейной алгебры |
| 32 |
|
| Тема 1.1 Матрицы и определители | Содержание учебного материала | 8 |
|
| Лекционное занятие. Матрицы и их виды. Операции над матрицами; определитель квадратной матрицы; свойства определителей; обратная матрица. | 2 | 2,3 |
| Практические занятия | 4 |
|
| Практическая работа №1. Выполнение операций над матрицами. Практическая работа №2. Вычисление определителей. | 2 2 | 3 |
| Самостоятельная работа студента №1 Решение упражнений: «Операции над матрицами»; «Определители квадратных матриц»; «Обратная матрица». Выполнение тестовых заданий «Виды матриц. Определители и их свойства» | 2 |
|
| Тема 1.2 Системы линейных уравнений | Содержание учебного материала | 10 |
|
| Лекционное занятие. Определение и основные понятия системы m линейных уравнений с n неизвестными. Методы решения систем линейных уравнений: метод Гаусса, формулы Крамера, метод обратной матрицы; численные методы решения уравнений и систем линейных уравнений. | 2 | 2,3 |
| Практические занятия | 4 |
|
| Практическая работа №3. Численные методы решения уравнений. Практическая работа №4. Решение систем линейных уравнений. | 2 2 | 2 |
| Самостоятельная работа студента №2 Решение упражнений: «Метод Гаусса для решения систем линейных уравнений»; «Решение систем линейных уравнений по формулам Крамера». Составление опорного конспекта «Метод обратной матрицы для решения систем линейных уравнений» Составление таблицы для систематизации учебного материала «Методы решения систем линейных уравнений» | 4 |
|
| Тема 1.3 Аналитическая геометрия | Содержание учебного материала | 8 |
|
| Семинарское занятие. Тема: Уравнение линии на плоскости. 1. Каноническое и параметрическое уравнение прямой; общее уравнение прямой и его частные случаи. 2. Другие формы уравнения прямой на плоскости; взаимное расположение двух прямых. 3. Кривые второго порядка: окружность, эллипс, гипербола, парабола. | 2 | 2,3 |
| Практические занятия | 2 |
|
| Практическая работа №5. Исследование прямой и кривых второго порядка на плоскости. | 2 | 2 |
| Самостоятельная работа студента №3 Решение упражнений: «Исследование взаимного расположения двух прямых на плоскости» «Построение кривых второго порядка» Составление таблицы для систематизации учебного материала «Кривые второго порядка» Выполнение тестовых заданий «Элементы аналитической геометрии» | 4 |
|
| Тема 1.4 Элементы теории линейных пространств | Содержание учебного материала | 6 |
|
| Лекционное занятие. Понятие линейного (векторного) пространства. Базис и размерность пространства; координаты вектора в базисе; евклидовы пространства; неравенство Коши-Буняковского; линейные операторы и их матрицы; собственные векторы и собственные значения линейных операторов. | 2 | 1,2 |
| Контрольная работа №1 | 2 |
|
| Самостоятельная работа студента №4 Решение упражнений: «Базис и размерность пространства» «Собственные векторы и собственные значения линейных операторов» | 2 |
| Раздел 2 Математический анализ |
| 70 |
| Тема 2.1. Введение в математический анализ | Содержание учебного материала | 10 |
| Семинарское занятие. Тема: Понятие функции; способы задания и свойства функции. 1. Обратная функция; основные элементарные функции, их свойства и графики; предел функции. 2. Основные теоремы о пределах функций; замечательные пределы; непрерывность функции. 3. Точки разрыва и их классификация; основные теоремы о непрерывных функциях. | 2 | 2,3
|
| Практические занятия | 4 |
|
| Практическая работа №6. Вычисление пределов функции. Практическая работа №7. Исследование функции на непрерывность. | 2 2 |
|
| Самостоятельная работа студента №5 Составление таблицы для систематизации учебного материала «Основные элементарные функции, их свойства и графики» Решение упражнений «Предел и непрерывность функции» | 4 |
|
| Тема 2.2 Дифференциальное исчисление | Содержание учебного материала | 12 |
|
| Семинарское занятие. Тема: Производная функции. 1. Геометрический и механический смысл производной; основные правила дифференцирования; таблица производных основных элементарных функций. 2. Производная сложной и обратной функции; производные высших порядков. 3. Дифференциал функции; признаки возрастания и убывания функции; экстремумы функции. 4. Выпуклость графика функции и точки перегиба; асимптоты графика функции; общая схема исследования функции и построение графиков. | 2 | 2,3
|
| Практические занятия | 4 |
|
| Практическая работа №8. Вычисление производной функции. Практическая работа №9. Исследование функции и построение ее графика. | 2 2 | 2,3 |
| Контрольная работа №2 | 2 |
|
| Самостоятельная работа студента №6 Составление опорного конспекта «Асимптоты графика функции» Решение упражнений: «Производная, ее геометрический и механический смысл»; «Построение графиков функций». Выполнение тестовых заданий «Приложение производной к исследованию свойств функции» Учебно-исследовательская работа «Применение производной к решению прикладных задач» | 4 |
|
| Тема 2.3 Интегральное исчисление | Содержание учебного материала | 10 |
|
| Семинарское занятие. Тема: Первообразная и неопределенный интеграл. 1. Свойства неопределенного интеграла; таблица основных интегралов; методы интегрирования. 2. Определенный интеграл и его геометрический смысл; свойства определенного интеграла; формула Ньютона-Лейбница. 3. Методы вычисления определенного интеграла; приложения определенного интеграла; приближенные методы вычисления определенных интегралов: формула прямоугольников, трапеций Симпсона. | 2 | 2,3
|
| Практические занятия | 4 |
|
| Практическая работа №10. Основные методы интегрирования. Практическая работа №11. Вычисление определенных интегралов. | 2 2 | 2,3 |
| Контрольная работа №3 | 2 |
|
| Самостоятельная работа студента №7 Решение упражнений: «Методы вычисления неопределенного интеграла»; «Методы вычисления определенного интеграла»; «Приложения определенного интеграла». Составление таблицы для систематизации учебного материала «Вычисление площадей плоских фигур» Учебно-исследовательская работа «Применение определенного интеграла к решению физических и технических задач» | 2 |
|
| Тема 2.4 Дифференциальные уравнения | Содержание учебного материала | 10 |
|
| Лекционное занятие. Дифференциальные уравнения первого порядка: основные понятия. Дифференциальные уравнения с разделяющимися переменными; однородные дифференциальные уравнения первого порядка; линейные дифференциальные уравнения первого порядка; простейшие дифференциальные уравнения второго порядка; численные методы решения задачи Коши, метод Рунге-Кутта. | 2 | 2 |
| Практические занятия | 4 |
|
| Практическая работа №12. Решение дифференциальных уравнений первого порядка. Практическая работа №13. Решение простейших дифференциальных уравнений второго порядка. | 2 2 | 2,3 |
| Контрольная работа №4 | 2 |
|
|
| Самостоятельная работа студента №8 Составление опорного конспекта «Задачи, приводящие к дифференциальным уравнениям» Решение упражнений: «Дифференциальные уравнения первого порядка»; «Дифференциальные уравнения второго порядка». Учебно-исследовательская работа «Дифференциальные уравнения в науке и технике» | 2 |
|
| Тема 2.5 Числовые и функциональные ряды | Содержание учебного материала | 10 |
|
| Лекционное занятие. Основные понятия и свойства числовых рядов. Необходимое условие сходимости числового ряда; признаки сходимости рядов с неотрицательными членами. Абсолютная и условная сходимость знакопеременных рядов. Признаки сходимости знакопеременных рядов; функциональные ряды; степенные ряды; область сходимость степенного ряда; основные свойства степенных рядов; ряд Тейлора; разложение элементарных функций в ряд Тейлора; применение степенных рядов. | 4 | 2 |
| Практические занятия | 2 |
|
| Практическая работа №14. Исследование на сходимость числовых и степенных рядов. | 2 | 2,3 |
| Самостоятельная работа студента №9 Составление опорного конспекта «Свойства числовых рядов» Решение упражнений: «Сходимость числовых рядов»; «Область сходимости степенного ряда». Выполнение тестовых заданий «Числовые и функциональные ряды» Учебно-исследовательская работа «Вычисление значений функции, определенных интегралов и решение дифференциальных уравнений при помощи степенных рядов» | 4 |
|
| Тема 2.6 Гармонический анализ | Содержание учебного материала | 8 |
|
| Лекционное занятие. Периодические функции. Разложение  в ряд Фурье при в ряд Фурье при 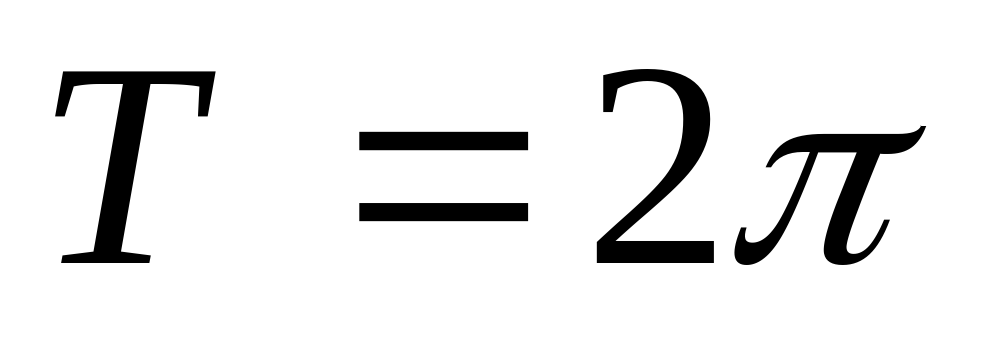 ; теорема Дирихле; ортогональные системы; разложение ; теорема Дирихле; ортогональные системы; разложение  в ряд Фурье при в ряд Фурье при 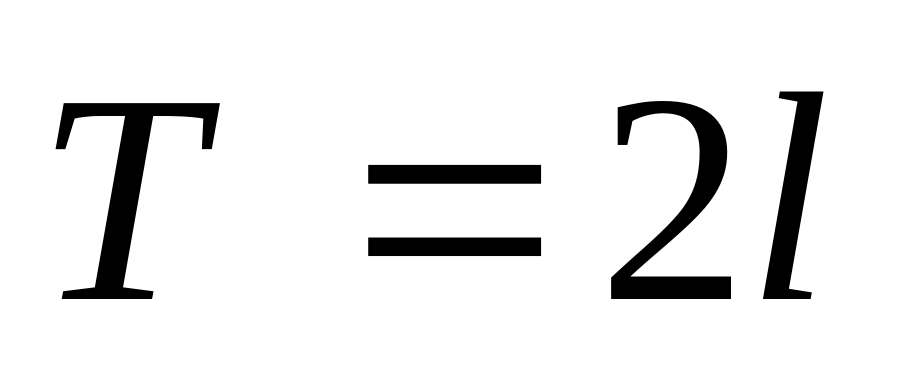 ; разложение ; разложение  в ряд Фурье только по косинусам или синусам. в ряд Фурье только по косинусам или синусам. Интеграл и преобразование Фурье. | 4 | 2 |
| Контрольная работа №5 | 2 |
|
| Самостоятельная работа студента №10 Решение упражнений: «Разложение в ряд Фурье функций, заданных на произвольном отрезке». Учебно-исследовательская работа «Применение рядов Фурье» | 2 |
|
| Тема 2.7 Функции комплексного переменного | Содержание учебного материала | 10 |
|
| Семинарское занятие. Тема: Понятие комплексного числа. 1. Алгебраическая форма комплексного числа; операции над комплексными числами. 2. Геометрическая интерпретация комплексного числа; тригонометрическая и показательная формы комплексного числа. Тема: Формула Эйлера. 1. Функции комплексного переменного. 2. Производная функции комплексного переменного. 3. Понятие о конформном отображении. Тема: Интеграл от функции комплексного переменного. 1. Ряды Тейлора и Лорана. 2. Выполнение действий над комплексными числами. 3. Дифференцирование и интегрирование функций комплексного переменного. | 6
2
2
2 | 2 |
| Самостоятельная работа студента №11 Составление опорного конспекта «Показательная форма комплексного числа» Решение упражнений: «Геометрическое представление комплексных чисел»; «Действия над комплексными числами в различных формах»; «Функции комплексного переменного» Учебно-исследовательская работа «Применение комплексных чисел». | 4 |
|
| Раздел 3 Элементы теории вероятностей и математической статистики |
|
|
|
| Тема 3.1 Элементы теории вероятностей | Содержание учебного материала | 12 |
|
| Семинарское занятие. Тема: Случайное событие. 1. Виды случайных событий. 2. Операции над событиями. 3. Вероятность события; свойства вероятности. Тема: Элементы комбинаторики. 1. Непосредственное вычисление вероятности. 2. Теоремы сложения и умножения вероятностей. 3. Формула полной вероятности; формула Байеса. Тема: Понятие дискретной случайной величины и ее закона распределения. 1. Числовые характеристики дискретной случайной величины: математическое ожидание и его свойства. 2. Дисперсия и ее свойства; среднее квадратическое отклонение. 3. Вычисление вероятности событий. 4. Определение числовых характеристик дискретной случайной величины. | 6 | 2
|
| Контрольная работа №6 | 2 | 2 |
| Самостоятельная работа студента №12 Решение упражнений: «Элементы комбинаторики»; «Применение теорем сложения и умножения для вычисления вероятности событий»; «Использование формул полной вероятности и Байеса для вычисления вероятности событий». Выполнение тестовых заданий «Теория вероятностей» | 4 |
|
| Тема 3.2 Элементы математической статистики | Содержание учебного материала | 6 |
|
| Лекционное занятие. Предмет и основные задачи математической статистики. Основные понятия математической статистики; виды выборок; группировка статистических данных. Числовые характеристики выборки: выборочная средняя, выборочная дисперсия, выборочное среднее квадратическое отклонение; статистическое оценивание. | 4 | 1 |
|
| Самостоятельная работа студента №13 Решение упражнений: «Числовые характеристики выборки»; «Статистическое оценивание». | 2 |
|
| Всего: | 120 |
4 условия реализации программы дисциплины 4.1 Требования к минимальному материально-техническому обеспечению
Реализация учебной дисциплины требует наличия учебного кабинета математики.
Оборудование учебного кабинета:
посадочные места по количеству обучающихся;
рабочее место преподавателя;
рабочие программы по математике, методическая литература;
комплект учебной литературы по математике;
электронные учебные издания;
демонстрационные печатные пособия;
электронное сопровождение учебных занятий;
дидактический материал по темам;
контрольно-измерительные материалы;
компьютерные тестовые программы.
Технические средства обучения:
персональный компьютер;
комплект лицензионного программного обеспечения;
мультимедийный проектор;
средства телекоммуникации.
4.2 Информационное обеспечение обучения Перечень рекомендуемых учебных изданий, Интернет-ресурсов
Основные источники:
Григорьев С.Г. Иволгина С.В. Математика: Учебник. – М.: «Академия», 2015. – 416 с.
Дополнительные источники:
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах.- М.: Высшая школа,2008
Калинина В.Н., Панкин В.Ф. Математическая статистика.- М.: Высшая школа,2006
Подольский В.А., Суходский А.М., Мироненко Е.С. Сборник задач по математике.- М.: Высшая школа,2005
Интернет-источники:
Математический портал (все книги по математике). [Электронный ресурс] – Режим доступа: http://math-portal.ru
Математика для колледжей. [Электронный ресурс] – Режим доступа: http://www.mathteachers.narod.ru
3. Математика за среднюю школу. [Электронный ресурс] – Режим доступа: http://www.mathematics.ru
5 Контроль и оценка результатов освоения Дисциплины Контроль и оценка результатов освоения учебной дисциплины осуществляется преподавателем в процессе проведения практических занятий, тестирования, а также выполнения обучающимися индивидуальных заданий, проектов, исследований.
| Результаты обучения (освоенные умения, усвоенные знания) | Формы и методы контроля и оценки результатов обучения |
| Освоенные умения: анализировать сложные функции и строить их графики; выполнять действия над комплексными числами; вычислять значения геометрических величин; производить операции над матрицами и определителями; решать задачи на вычисление вероятности с использованием элементов комбинаторики; решать прикладные задачи с использованием элементов дифференциального и интегрального исчислений; решать системы линейных уравнений различными методами; | текущие контрольные работы; итоговые контрольные работы письменная проверка
|
| Усвоенные знания: основные математические методы решения прикладных задач; основные понятия и методы математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики; основы интегрального и дифференциального исчисления; роль и место математики в современном мире при освоении профессиональных дисциплин и в сфере профессиональной деятельности.
| текущие контрольные работы; итоговые контрольные работы устный опрос; стандартизированный контроль
|
Перечень теоретических вопросов к дифференцированному зачету
Функция одной независимой переменной
Предел функции. Замечательные пределы.
Непрерывность функции. Исследование функции на непрерывность.
Производная. Правила дифференцирования.
Производная. Физический и геометрический смысл производной.
Неопределенный интеграл и его свойства.
Определенный интеграл и его свойства.
Геометрический смысл определенного интеграла. Вычисление площадей плоских фигур с помощью определенного интеграла.
Матрицы, их виды. Действия над матрицами.
Умножение матриц, обратная матрица.
Определители n-го порядка, их свойства и вычисление.
Миноры и алгебраические дополнения. Разложение определителей в сумму алгебраических дополнений.
Решение СЛАУ методами линейной алгебры. Формулы Крамера.
Матричный метод решения СЛАУ.
Метод Гаусса.
Множества. Способы задания множеств.
Операции над множествами.
Отношения, свойства отношений.
Определение графа. Элементы графа. Виды графов.
Комплексное число и его формы.
Действия над комплексными числами в различных формах
Определение размещения. Формула для расчета количества размещений.
Определение перестановки. Формула для расчета количества перестановок.
Определение сочетания. Формула для расчета количества сочетаний.
Событие. Виды событий. Операции над событиями.
Вероятность события. Частота события.
Классическое определение вероятности события.
Теоремы сложения и умножения вероятностей.
Случайная величина, ее виды. Закон распределения случайной величины.
Числовые характеристики случайной величины.
Генеральная совокупность и выборка. Статистическое распределение выборки. Полигон и гистограмма.
Перечень практических заданий.
Найти предел: 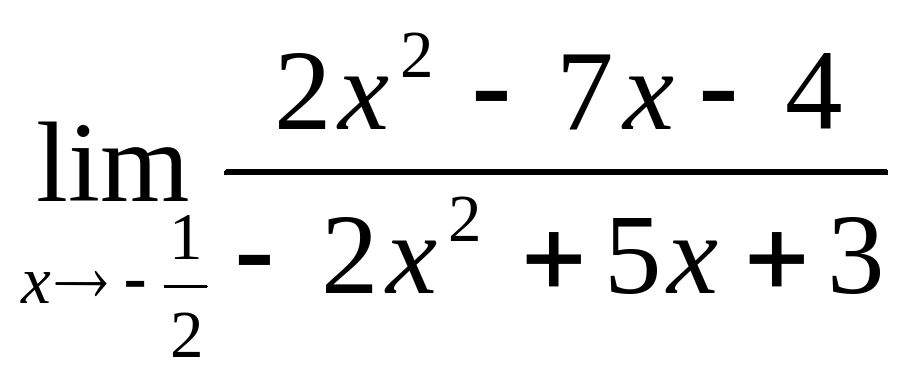
Найти предел: 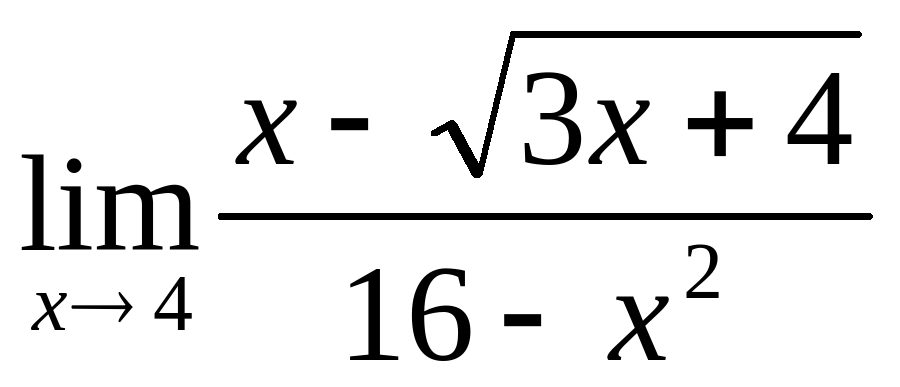
Найти предел: 
Найти предел: 
Найти предел: 
Найти предел: 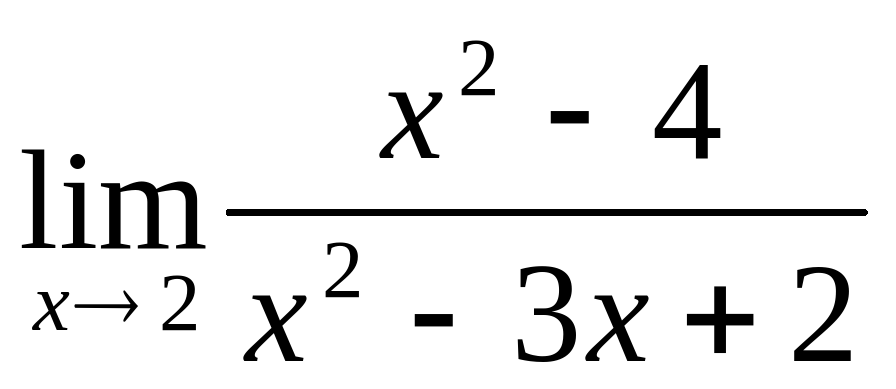 .
.
Найти предел: 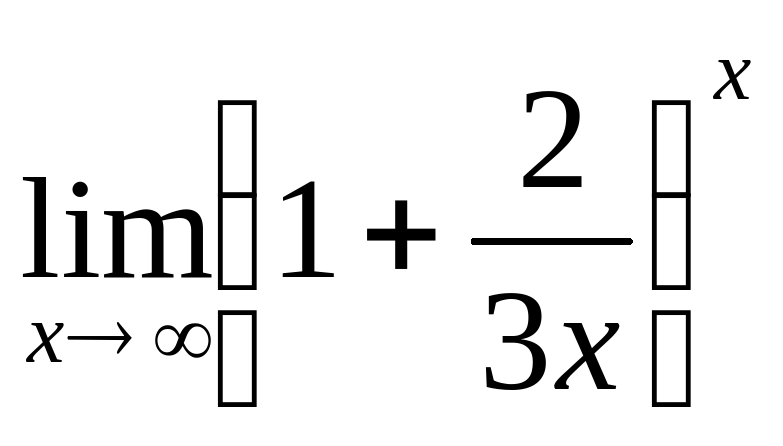
Найдите производную функции: 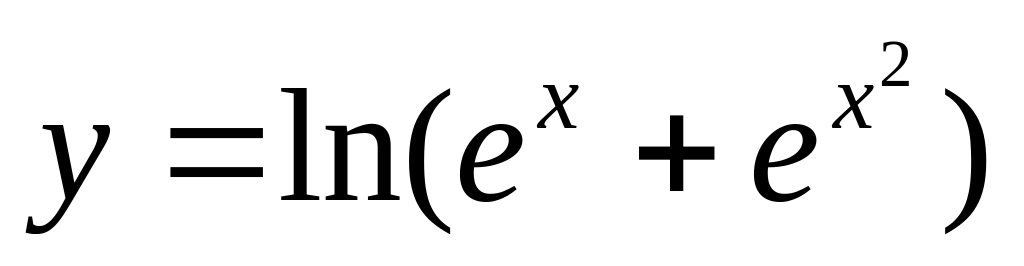 .
.
Найдите производную функции: у = arcsin(4x2 – x3).
Найдите производную функции: у = sin x∙(cos x – 4)
Найдите производную функции: у = 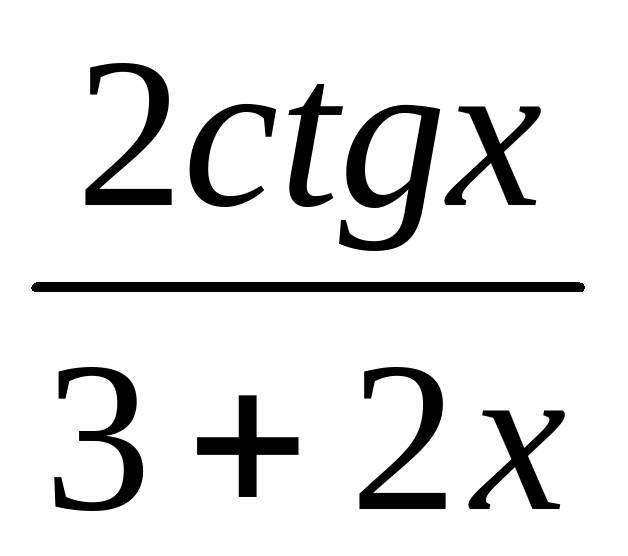
Найдите производную функции: у=(7х3 – 3х7)13
Найдите производную функции: у = 
Вычислите интеграл: 
Вычислите интеграл: 
Вычислите интеграл: 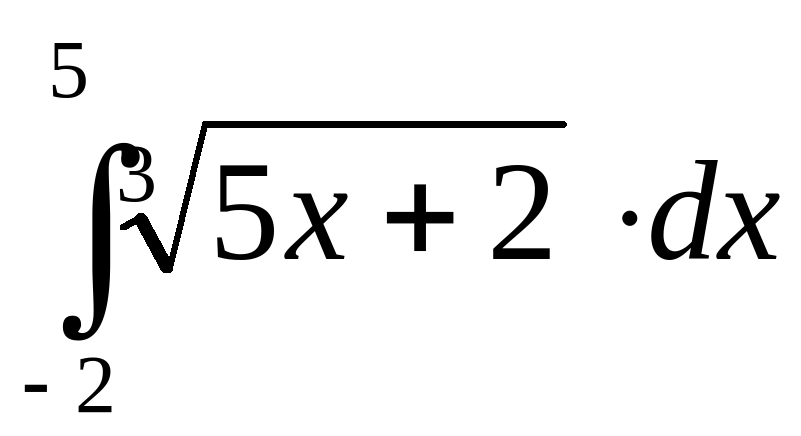
Вычислите интеграл: 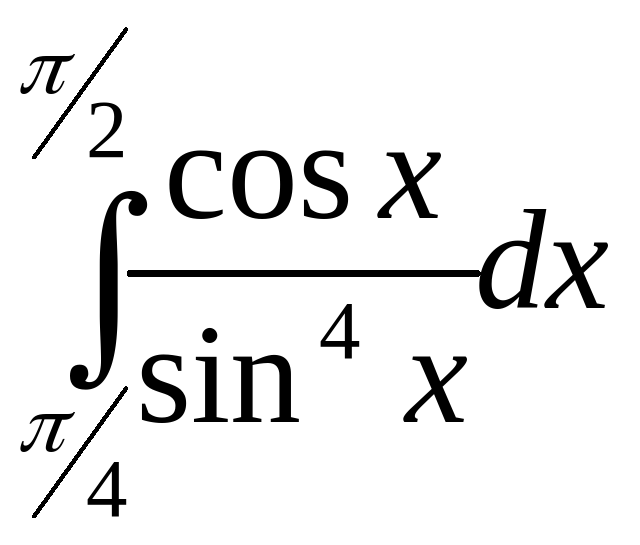 .
.
Вычислите интеграл:  .
.
Вычислите интеграл: 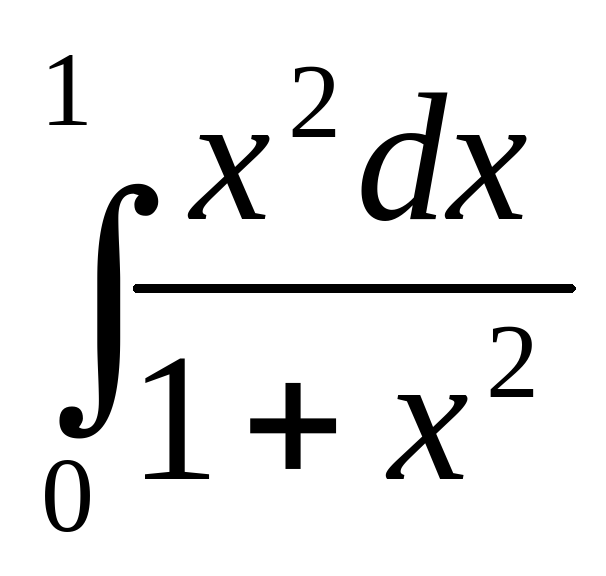 .
.
Вычислите площадь фигуры, ограниченной линиями: у = х3 и у = 4х. Постройте график.
Вычислите площадь между линиями у1 = 2х – х2 и у2 = 0. Изобразите эту площадь графически.
22.Выполните действия: �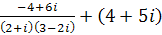 �
�
23. Выполните действия: � �
�
24.�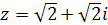 � . Найдите �
� . Найдите �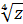 �.
�.
25.Представьте в алгебраической форме число � �.
�.
Изобразите это число на комплексной плоскости и найдите его модуль и аргумент.
26.Какое из заданных отношений на множестве N обладает свойством
симметричности?
«число х больше числа у на2»
«число х делится на число у без остатка»
«х+у- нечетное число»
«х-у=1
27.Чему равна степень вершины А заданного графа
28.Даны множества � �.
Найдите разность множеств А и В
29. Вычислить определитель:
30. Вычислить матрицу D = (BA) - C, если
6







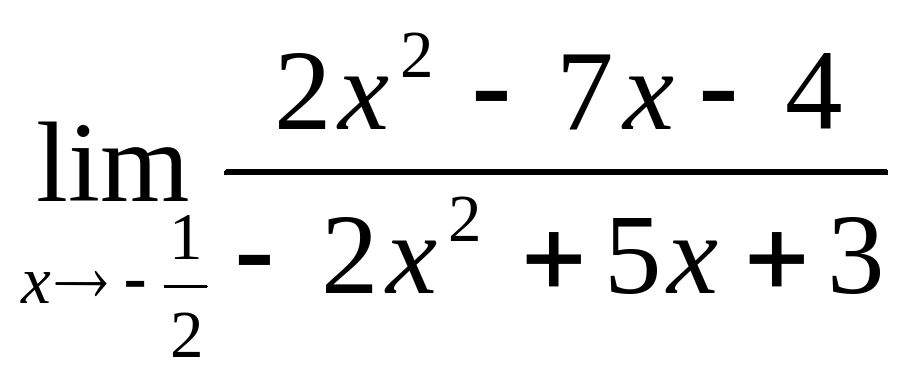
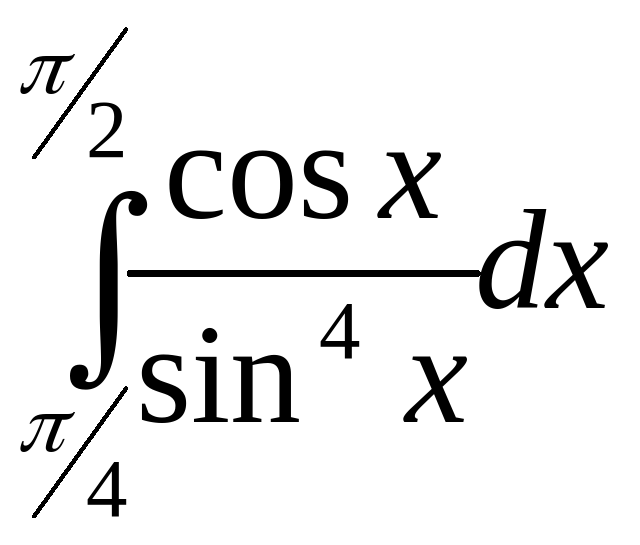 .
.
















