Разбор заданий по геометрии при подготовке к ОГЭ №16_КАСАТЕЛЬНАЯ, ХОРДА, СЕКУЩАЯ, РАДИУС

Разбор заданий ОГЭ №16

КАСАТЕЛЬНАЯ, ХОРДА, СЕКУЩАЯ,

РАДИУС

Разобрать и законспектировать!

Задача 1

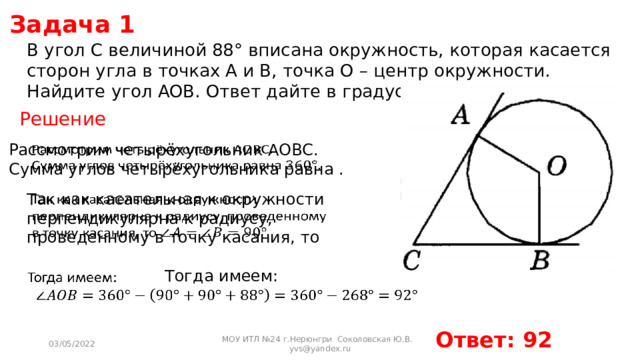
В угол C величиной 88° вписана окружность, которая касается сторон угла в точках A и B, точка O – центр окружности. Найдите угол AOB. Ответ дайте в градусах.

Решение

Рассмотрим четырёхугольник AOBC.

Сумма углов четырёхугольника равна .

Так как касательная к окружности перпендикулярна к радиусу, проведенному в точку касания, то

Тогда имеем:

Ответ: 92

03/05/2022

МОУ ИТЛ №24 г.Нерюнгри Соколовская Ю.В. yvs@yandex.ru

Задача 2

Касательные в точках A и B к окружности с центром O пересекаются под углом 66°. Найдите угол ABO. Ответ дайте в градусах.

Решение

Так как отрезки касательных к окружности, проведенные из одной точки, равны, то равнобедренный.

Угол между касательной и хордой равен половине дуги, которую он заключает, значит, дуга AB равна

Угол AOB – центральный, а градусная мера центрального угла (вершина в центре окружности) равна градусной мере соответствующей дуги окружности.

А так как равнобедренный (AO=OB - радиусы), то получим:

Ответ: 33

03/05/2022

МОУ ИТЛ №24 г.Нерюнгри Соколовская Ю.В. yvs@yandex.ru

Задача 3

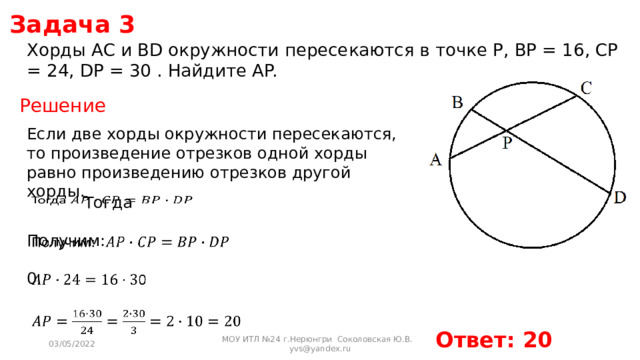
Хорды AC и BD окружности пересекаются в точке P, BP = 16, CP = 24, DP = 30 . Найдите AP.

Решение

Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

Тогда

Получим:

0

Ответ: 20

03/05/2022

МОУ ИТЛ №24 г.Нерюнгри Соколовская Ю.В. yvs@yandex.ru

Задача 4

На окружности отмечены точки A и B так, что меньшая дуга AB равна 138°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Решение

Угол между касательной и хордой равен половине дуги, которую он заключает.

По условию

   AB 

Поэтому

Задачу можно решить и другим способом!

Ответ: 69

03/05/2022

МОУ ИТЛ №24 г.Нерюнгри Соколовская Ю.В. yvs@yandex.ru

Задача 5

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 5, AC = 20. Найдите AK.

Решение

Квадрат отрезка касательной равен произведению секущей на ее внешнюю часть. Тогда

Получим:

AK=10

Ответ: 10

03/05/2022

МОУ ИТЛ №24 г.Нерюнгри Соколовская Ю.В. yvs@yandex.ru

Задача 6

Найдите угол АСО, если его сторона СА касается окружности, О – центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 128°.

Решение

- развёрнутый

 AD 

Тогда  AВ 

Угол AOB – центральный, а градусная мера центрального угла (вершина в центре окружности) равна градусной мере соответствующей дуги окружности.

Так как касательная к окружности перпендикулярна к радиусу, проведенному в точку касания, то

Имеем:

Ответ: 38

03/05/2022

МОУ ИТЛ №24 г.Нерюнгри Соколовская Ю.В. yvs@yandex.ru

Задача 7

Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3 : 6 : 9. Найдите радиус окружности, если меньшая из сторон равна 8.

Решение

Длины дуг относятся так же, как их градусные меры. Пусть x – одна часть градусной меры, тогда первая дуга будет 3x, вторая 6x, а третья – 9x.

Так как все три дуги образуют полную окружность 360 градусов, то составим уравнение:

Тогда меньшая дуга окружности будет:

Угол треугольника, опирающийся на эту дугу является вписанным, поэтому он равен половине дуги: 

Меньший угол треугольника лежит против меньшей стороны. Найдём радиус описанной окружности. По теореме синусов получим:

16

8

Ответ: 8

03/05/2022

МОУ ИТЛ №24 г.Нерюнгри Соколовская Ю.В. yvs@yandex.ru

Задача 8

Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а

расстояние от точки А до точки О равно 12.

Решение

Проведём радиусы OB и OC в точки касания. Получили два прямоугольных треугольника.

B

по двум сторонам и углу между ними (OB=OC радиусы, OA – общая,

Из равенства треугольников

Тогда

C

Ответ: 6

03/05/2022

МОУ ИТЛ №24 г.Нерюнгри Соколовская Ю.В. yvs@yandex.ru