АДМИНИСТРАЦИЯ ГОРОДА СМОЛЕНСКА
муниципальное бюджетное общеобразовательное учреждение
«Средняя школа № 9» города Смоленска
(МБОУ «СШ № 9»)
ПРОЕКТ
Решение некоторых задач закрытой части ОГЭ по математике из модуля «геометрия»
Выполнил работу: Саражинская Анастасия Андреевна,
учащийся 9 «Б» класса
Руководители: Филатова Татьяна Юрьевна,
Преподаватель математики,
математика
Смоленск
2019
Введение
Математика – царица наук. С первого класса на уроках математики мы изучаем геометрические фигуры.
Геометрические фигуры окружают каждого из нас в повседневной жизни. И люди давно заинтересовались их разнообразием, строением и их свойствами. Так появилась наука геометрия, позволяющая изучать геометрические фигуры, с которой мы познакомились в старших классах.
Этот предмет в школе считается одним из важных. Но к сожалению, он воспринимается намного сложнее остальных предметов, а времени на изучение этой науки в школе отводится значительно меньше, чем на другие уроки. Это является одной из причин, почему геометрию сложнее воспринимать ученикам.
У большинства моих одноклассников, как и других учеников, сложности возникают именно при решении задач по геометрии.
Геометрия сложна и требует точных расчетов. Не смотря на трудности, я стараюсь сама разобраться в поставленных задачах. И так, как по расчетам в ОГЭ по математике наибольший процент нерешенных задач приходится на модуль «геометрия», моя главная задача в этом проекте – помочь одноклассникам и желающим разобраться с этой проблемой, объяснив и подробно разобрав несколько наиболее сложных задач по этой теме
Актуальность темы
Почему я выбрала эту тему?
В мире почти во всем можно увидеть геометрические фигуры. Например, самая обычная комната состоит из прямоугольников, если смотреть на нее с точки зрения геометрии. Книга –тот же самый прямоугольник. А футбольный или волейбольный мяч? Это шар. Более сложные предметы, например, машину, можно представить в нескольких прямоугольниках, различных по длине и ширине, колоса – это окружность и так далее. На что бы мы не посмотрели, любой предмет можно разложить на геометрические фигуры. И знания геометрии нужны. Сейчас я попробую это доказать.
Предположим, вам необходимо переклеить обои в комнате. Для начала вам нужно рассчитать площадь стен – а*b, где а-длина, b-ширина. Потом вы идете в магазин, находите нужные обои, и чтобы не просчитаться, вам опять нужно вычислить площадь, но уже обоев. Можно привести множество таких примеров, где нужно знать именно этот раздел в математике: сколько воды потребуется, чтобы наполнить емкость? Какой длины должна быть лестница, чтобы залезть на крышу? И много еще задач, с разными сложностями, с которыми мы встречаемся в повседневной жизни, и которые могут вызвать затруднение.
Основная проблема состоит в том, что большинство людей не знает геометрию. И мне кажется, я знаю в чем проблема.
По моим расчетам, на изучение блока «геометрия» в школе отводится мало времени, примерно в 2 раза меньше, чем на блок «алгебра» и на многие предметы в школе. Я считаю, что этого недостаточно для усвоения этого урока, а воспринимается он намного сложнее остальных. Да и сами ученики не хотят в свое свободное время заниматься дополнительно этим предметом, который их не интересует. Многим кажется, что в дальнейшем она им не пригодится и все, что им надо они уже знают.
Прошу заметить еще вот что: традиционно в ОГЭ и ЕГЭ по математике наибольший процент нерешенных задач приходится как раз на модуль «геометрия». Поэтому, моя главная задача в этом проекте – подтянуть самой этот предмет и помочь одноклассникам и всем желающим разобраться с этой проблемой, понятно объяснив и подробно разобрав несколько задач из закрытой части ОГЭ по математике в блоке «геометрия»
Цель: разобраться в данных задачах, помочь другим и доступно объяснить, как они решаются.
Задачи: подробно разобрать задачи, которые вызывают наибольшие затруднения.
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ, НЕОБХОДИМЫЙ ДЛЯ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ 1-Й ЧАСТИ ОГЭ
Треугольники
Треугольник – это 3 точки, не лежащие на одной прямой, соединенные отрезками. Отмеченные три точки – вершины треугольника. Три отрезка – стороны треугольника.
Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса – это отрезок, соединяющий вершину треугольника с противоположной стороной и делящий угол пополам.
Высота – перпендикуляр, опущенный из вершины треугольника к противоположной стороны.
Средняя линия – линия, соединяющая середины двух сторон и равна половине третьей стороны и параллельна ей
Сумма всех углов треугольника равна 180̊. S=⅟2аh, где а – сторона, h – высота, опущенная к этой стороне. Р=а+с+b, где а, с и b – стороны треугольника.

![]()





В ВН – высота, ˪Н – прямой


СЕ – биссектриса, ˪ВСЕ=˪ЕСА


Е М СА – медиана, ВМ=МС

̢ ˪ВАС+˪АСВ+˪СВА=180̊
![]()
![]()
ЕМ – средняя линия, ЕМ=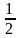 АС, ЕМ‖АС
АС, ЕМ‖АС
А Н С
Равнобедренный треугольник – треугольник, у которого две стороны равны. Равные стороны называются боковыми, а третья сторона – основание. В равнобедренном треугольнике углы при основании равны; биссектриса является высотой и медианой.

![]()
В АВ=ВС; ˪А=˪С
АВ, ВС – боковые стороны
АС – основание
![]()
![]()


ВН – высота, биссектриса, медиана
А Н С
Равносторонний треугольник – треугольник, у которого все стороны равны. В равностороннем треугольнике все углы равны и равны 60̊. S=(а²√30):4

В АВ= ВС=СА


˪А=˪В=˪С=60̊

А С
Прямоугольный треугольник – треугольник. У которого один из углов прямой 9 равен 90̊). Сторона, лежащая напротив прямого угла – гипотенуза, а две другие стороны – катеты. Сумма двух острых углов равна 90̊. Катет прямоугольного треугольника, лежащий напротив угла в 30̊, равен половине гипотенузы. S=⅟2аb, где а и b – катеты.



гипотенуза
катет
В ВС- гипотенуза, ВА и АС – катеты
˪А=90̊
˪В=30̊ =› АС=⅟2 ВС
![]()
![]()

катет
˪В+˪С=90̊
А С
Синус острого угла прямоугольного треугольника– это отношение противоположного катета к гипотенузе.
Косинус острого угла прямоугольного треугольника – это отношение прилежащего катета к гипотенузе.
Тангенс острого угла прямоугольного треугольника – это отношение противоположного катета к прилежащему.
Тангенс угла равен отношению синуса к косинусу этого угла.
Таблица синусов, косинусов и тангенсов углов.
| а | 30̊ | 45̊ | 60̊ |
| sin | ⅟2 | √2∕2 | √3∕2 |
| cos | √3∕2 | √2∕2 | ⅟2 |
| tg | √3∕3 | 1 | √3 |
Внешний угол треугольника – угол, смежный внутреннему углу треугольника при этой вершине.
Сумма смежных углов равна 180̊.
Сумма внешнего и внутреннего углов, при одной вершине, равна 180̊.
Внешний угол равен сумме двух углов, не смежных с ним.

А ˪АСМ – внешний угол, ˪АСВ – внутренний угол
˪АСМ+˪ВСА=180̊;

внешний угол
˪АСМ=˪САВ=˪АВС

В С М
Подобные треугольники
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Число k – коэффициент подобия, он равен отношению сторон одного треугольника к сходственным сторонам другого треугольника.
Отношение площадей двух подобных треугольников равно квадрату коэффициенту подобия этих треугольников.


В В1 ∆АВС≈∆А1В1С1 (≈ – подобны)
АВ и А1В1, ВС и В1С1; АС и А1С1-сходственные стороны
˪А=˪А1; ˪В=˪В1; ˪С=˪С1
А С k= =
= =
= 
А1 С1
Признаки подобия треугольников
-
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
-
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы между ними равны, то такие треугольники подобны.
-
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то они подобны.
Признаки равенств треугольников
-
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.
-
Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
-
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Четырехугольники
В любом четырехугольнике есть четыре стороны и четыре вершины. Две несмежные стороны и две вершины, не лежащие на одной прямой, называются противоположными. Сумма двух смежных углов равна 180̊, а сумма всех углов равна 360̊.
Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны. В параллелограмме противоположные стороны равны и противоположные углы равны. Сумма двух односторонних углов равна 180̊. Диагонали параллелограмма точкой пересечения делятся пополам. Накрест лежащие углы равны. S=aha, где а – сторона, h – высота, опущенная к стороне а.



В С АВ‖СD, ВС‖А; ВА=СD, ВС=АD




O ˪АВС=˪СDА, ˪ВСА=˪DАВ



ВО=DO, СО=АО
А D ˪ВАD+˪АВС=˪ВСD+˪СDА=180̊
˪АВD=˪СDВ, ˪СВD=ВDА, ˪ВСА=˪DАС, ˪ВАС=˪АСD –
(как накрест лежащие углы)
Трапеция – четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны трапеции называют ее основаниями, а две другие – боковыми сторонами. Сумма односторонних углов равна 180̊. S=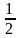 (а+b)h. S=МНh.
(а+b)h. S=МНh.
Средняя линия трапеции – линия, соединяющая боковые стороны трапеции и делящая их пополам. Средняя линия трапеции равна полусумме ее оснований.



боковая сторона
основание
В С ВС‖АD, АD и ВС – основание




боковая сторона
ВА и СD – боковые стороны
![]()





М Н
М
˪А+˪В=˪С+˪D=180̊

основание
МН – средняя линия; МН= 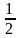 (ВС+АD)
(ВС+АD)
А D
Равнобедренная трапеция – трапеция, у которой боковые стороны равны. В равнобедренной трапеции углы, лежащие у одного основания равны.

В С ВС‖АD

ВА=СD

˪А=˪D, ˪В=˪С
˪А+˪В=˪С+˪D=180̊
А D


Прямоугольная трапеция – трапеция, у которой один из углов прямой. S=MH∙АВ



В С

![]()







![]()
![]()
![]()

![]()
М Н
ВС‖АD
ВА=СD
˪А=˪В=90̊

А D
˪А+˪В=˪С+˪D=180̊; ˪В+˪С=˪А+˪D=180̊
S=MH∙АВ
Прямоугольник – четырехугольник, у которого все углы прямые. Диагонали прямоугольника равны и точкой пересечения делятся пополам. Противолежащие стороны равны. S=аb.


![]()






![]()
![]()
![]()
В С АВ=СD; ВС=АD
![]()
АВ‖СD; ВС‖АD


О
ВD=АС
![]()
![]()

![]()
А D ˪А=˪В=˪С=˪D=90̊
Квадрат – параллелограмм, у которого все углы прямые и все стороны равны. Диагонали квадрата равны, взаимно перпендикулярны. Точкой пересечения делятся пополам и делят углы квадрата пополам.


![]()
![]()
![]()
![]()
 В С ВО=СО=АО=DО
В С ВО=СО=АО=DО


ВА=АD=DС=СВ


˪А=˪В=˪С=˪D=90


О ˪ВОА=˪ВОС=˪СОD=˪DОА=90̊
![]()
![]()


А D
Ромб –параллелограмм, у которого все стороны равны. Диагонали ромба взаимно перпендикулярно и делят его углы пополам и делят ромб на 4 равных треугольника.


С АВ=ВС=СD=DА


СD=АО; ВО=ОD



В D ˪ВОА=˪АОD=˪DОС=˪СОВ=90̊


А
Окружность
Окружность – замкнутая кривая, которая состоит и всех точек на плоскости, равноудаленных от центра. S=r2∙3,14. Окружность равна 360̊.
Радиус – отрезок, соединяющий центр окружности с какой-либо точкой окружности (R, r)
Хорда –отрезок, соединяющий две любые точки окружности, не проходящий через центр окружности. Если две хорды окружности пересекаются. То произведение отрезков одной хорды равно произведению отрезков другой хорды.
Диаметр – наибольшая хорда, проходящая через центр окружности. (D, D=2R)

![]()
D АВ – хорда


А М СD – диаметр; СD=2ОM

О ОМ – радиус
В
С
Касательная к окружности
-
Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая имеет две общие точки с окружностью.
-
Если расстояние оотцентра окружности до прямой равно радиусу окружности, то прямая имеет тоько одну общую точку с окружностью.
-
Если расстояние от окружности до прямой больше радиуса окружности, то прямая не имеет общих точек сокружностью.
















C ОВr, = прямая имеет 2 общие точки с окр.
В ОС=r, = прямая имеет 1 общую точку с окр.

о ОАr, = прямая не имеет общих точек с окр.
А
Точки, лежащие на окружности, делят эту окружность на дуги. Чтобы различать дуги на них отмечают промежуточную точку. Дуга называется полуокружностью, если соединенные ее концы являются диаметром.

![]()

М
K ‿АLВ; ‿АСВ; ‿МКА; ‿МLА

А МВ – диаметр

о L ‿МСВ=‿МLВ=180̊ – полуокружности

C
В
Вписанный угол – угол, вершина которого лежит на окружности, а стороны угла пересекают окружность. Вписанный угол равен половине дуги, на которую он опирается. Вписанные углы, опирающиеся на одну и ту же дугу равны. Вписанный угол, опирающийся на полуокружность – прямой.
Центральный угол – угол, вершина которого лежит в центре окружности. Центральный угол равен дуге, на которую он опирается.

Е






А В ˪АFВ=˪АСВ=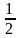 ‿АЕВ– вписанные углы
‿АЕВ– вписанные углы

о АОВ=‿АLВ – центральный угол
С F
РАЗБОР ЗАДАНИЙ ВАРИАНТОВ ОГЭ
Задание 16 Треугольники, четырёхугольники, многоугольники и их элементы (КИМ ОГЭ)
Задача №1
В треугольнике АВС известно, что АВ=8, ВС=10, АС=14. Найдите cos
Дано: ∆АВС
АВ=8, ВС=10, АС=14
Найти: cos
Решение:
142 =82+102-2·8·10·cos
196=64+100-160·cos
160·cos
160·cos
cos =- =-0,2
=-0,2
Ответ: -0,2
Попробуйте решить подобную задачу:
В треугольнике АВС известно, что АВ=8, ВС=10, АС=12. Найдите cos
Задача №2
В треугольнике АВС угол А равен 30̊, угол В равен 45̊, ВС=8 . Найдите АС
. Найдите АС
Дано: ∆АВС
ВС=8
Найти: АС
Решение:
 =
= (по теореме синусов)
(по теореме синусов)
АС=
АС= =
= =
= =
= =16
=16
Ответ: 16
Попробуйте решить подобную задачу:
В треугольнике АВС угол А равен 45̊, угол В равен 60̊, ВС= . Найдите АС.
. Найдите АС.
Задача №3
Биссектриса равностороннего треугольника равна 9 . Найдите его сторону.
. Найдите его сторону.

 В Дано: ΔАВС
В Дано: ΔАВС
ВК=9 – биссектриса
– биссектриса
А К D Найти: сторону АВС
Решение:
Рассмотрим ΔВСК – он прямоугольный, ˂К=90 - т.к. в равностороннем треугольнике биссектриса является медианой и высотой
˂В=60 :2=30°,
:2=30°,
˂С=60 (по условию)
sin˂C=
 =
=
ВС=
ВС=9‧2=18
Ответ: 18
Попробуйте решить подобную задачу:
Биссектриса равностороннего треугольника равна 5 . Найдите его сторону.
. Найдите его сторону.
Задание 17 Окружность, круг и их элементы (КИМ ОГЭ)
Задача №1
В угол величиной в 107° вписана окружность, которая касается сторон угла в точках А и В, точка О - центр окружности, Найдите угол АОВ, ответ дайте в градусах.
Дано: окр(О,r)
Найти:
Решение:
∆АВС - вписанный (по условию)
⇒
АОВ=90°⇒
∆АВС - прямоугольный
АВ - гипотенуза, АВ=2r=10·2=20
АС2+СВ2=АВ2
162+СВ2=202
СВ2=202-163=400-256=144
СВ= =12
=12
Ответ: 12
Попробуйте решить подобную задачу:
В угол С величиной 84° вписана окружность, которая касается сторон угла в точках А и В, точка О - центр окружности. Найдите угол АОВ. Ответ дайте в градусах
Задача №2
Периметр треугольника равен 140, одна из сторон равна 56, а радиус вписанной в него окружности равен 9. Найдите площадь этого треугольника.
Д ано: Р∆авс=140
АС=56
r=9
Найти: S∆авс
Решение:
S=pr
p=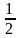 P=
P=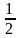 140=70
140=70
S=70·9=630
Ответ: 630
Попробуйте решить подобную задачу:
Периметр треугольника равен 120, дна из сторон равна 40, а радиус вписанной в него окружности равен 7. Найдите площадь этого треугольника.
Задача №3
К асательные в точках А и В к окружности с центром О пересекаются под углом 88°. Найдите угол АВО. Ответ дайте в градусах.
Дано: окр(О;r)
Найти: ˂АВО
Решение:
ΔАОВ – равнобедренный, т.к. АО и ОВ - радиусы⇒󠄀
˂АОВ=˂ОВА=(180°-88°):2=92°:2=46°
Ответ: 46°
Попробуйте решить подобную задачу:
Касательные в точках А и В к окружности с центром О пересекаются под углом 75°. Найдите угол АВО. Ответ дайте в градусах.
Задание 18 Площади фигур. (КИМ ОГЭ)
Задача №1
Сторона ромба равна 12, а расстояние от точки пересечения диагоналей ромба до нее равно 1. Найдите площадь ромба.
В С Дано: АВСD – ромб
O АD=12, ОН=1
А D Найти: SАВСD
Решение:
Диагонали ромба делят его на 4 равных треугольника⇒󠄀
Рассмотрим ΔАОD
SΔAOD=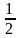 12‧1=6‧1=6
12‧1=6‧1=6
В ромбе АВСD 4 ΔАОD⇒󠄀
АВСD=4‧6=24
Ответ: 24
Попробуйте решить подобную задачу:
Сторона ромба равна 4, а расстояние от точки пересечения диагоналей ромба до нее равно 1. Найдите площадь ромба.
Задача №2
Основания трапеции равны 1 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
В С Дано: АВСD – трапеция
L М N LM – средняя линия
АС – диаметр
А D Найти: LM, MN
Решение:
Рассмотрим ΔАВС
LM=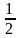 ВС=
ВС=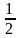 1=0,5 (т.к. LM - средняя линия ΔАВС и равна
1=0,5 (т.к. LM - средняя линия ΔАВС и равна 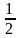 ее основания)
ее основания)
Рассмотрим ΔАСD
МN=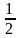 АD=
АD=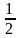 11=5,5
11=5,5
Ответ: 5,5
Попробуйте решить подобную задачу:
Основания трапеции равны 8 и 5. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Задача №3
В равнобедренной трапеции известна высота 5, меньшее основание 3 и угол при основании 45°. Найдите большее основание.
D C Дано: АВСD – трапеция
ВС=3, ВН=5,
А D ˂А=45°
H Найти: АD
Решение:
˂АНВ=90° т.к. ВН – высота
Рассмотрим ΔАВН
˂АВН=90°-˂ВАН=90°-45°=45° ⇒󠄀 ΔАВН – равнобедренный ⇒󠄀
АН=ВН=5
Опустим высоту из вершины С
Рассмотрим НВСN – это квадрат т.к. все углы равны ⇒󠄀
ВС=НN=3
АН=ND=5 т.к. трапеция равнобедренная
АD=АН+НN+ND=5+3+5=13
Ответ: 13
Попробуйте решить подобную задачу:
В равнобедренной трапеции известна высота 7, меньшее основание 4 и угол при основании 45°. Найдите большее основание.
Задача №4
Периметр квадрата равен 60. Найдите площадь этого квадрата.
 В С Дано: АВСD – квадрат
В С Дано: АВСD – квадрат
Р=60
А D Найти: S
Решение:
Р=4а
4а=60
а= =15
=15
S=а2=152=225
Ответ: 225
Попробуйте решить подобную задачу:
Периметр квадрата равен 90. Найдите площадь этого квадрата.
Заключение
С самого начала этого учебного года преподаватель давала варианты ОГЭ по математике каждому ученику, которые мы должны были решить за неделю. Большинство неправильно решенных задач у меня были из модуля «геометрия», так же и у большинства моих одноклассников. И так как моя главная цель в этом проекте была разобраться с этой проблемой, я с ней справилась.
В конце третьей четверти все девятиклассники писали пробный экзамен по математике. На этот раз я смогла решить правильно все задания из блока «геометрия» первой части, а также попробовала решить одно задание из второй части блока «геометрия».
После этого преподаватель неоднократно раздавала нам варианты ОГЭ, но на этот раз мы должны были решить его за один урок. Несмотря на это, все задачи по геометрии я решила правильно.
Так же я помогала своим одноклассникам разобраться с наиболее легкими заданиями, которые вызвали у них затруднения. После этого они смогли сами их решить на пробном экзамене.
Таким образом я могу сказать, что успешно выполнила поставленные мной цели и задачи в данном проекте.
















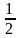 АС, ЕМ‖АС
АС, ЕМ‖АС 

























