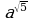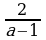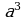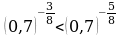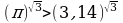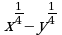СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Разработка методического кейса по теме « Действительные числа» по предмету «Алгебра и начала математического анализа в 10 классе
Данный методический продукт позволяет эффективнее использовать время учителя как на уроке, так и при подготовке к уроку. В представленных далее разработках сделан акцент на практическое применение знаний учащихся, полученных в процессе обучения. Об этом свидетельствует подобранное большое количество практических упражнений на каждом уроке
Просмотр содержимого документа
«Разработка методического кейса по теме « Действительные числа» по предмету «Алгебра и начала математического анализа в 10 классе»
АННОТАЦИЯ
Данная работа является методической разработкой по предмету «Алгебра и начала математического анализа» и включает цикл уроков для 10 класса по теме: «Действительные числа», на изучение которой отводится: 14 часов (3 часа в неделю).
Каждый урок содержит методический материал для учителя: теоретическую и практическую часть. Помимо методического материала для учителя в разработке предложены материалы для учащихся.
Цель исследования – разработка методического кейса по предмету «Алгебра и начала математического анализа» для 10 класса по теме: «Действительные числа».
Для достижения поставленной цели необходимо решить следующий комплекс задач:
изучить структуру современного урока и проблему методического обеспечения уроков предмета «Алгебра и начала математического анализа» в педагогической и методической литературе;
проанализировать требования учебной программы к уровню знаний и умений учащихся 10 классов по теме: «Действительные числа»;
разработать цикл уроков для 10 класса по теме: «Действительные числа».
Данная выпускная работа как методический продукт рассчитана как на начинающих педагогов, так и на учителей, имеющих большой опыт работы. Она позволит учителю всесторонне подготовиться к занятию, а также показать при этом высокие результаты во владении теоретическим материалом и решении практических задач, повысит общий уровень знаний по предмету.
ВВЕДЕНИЕ
Поиск путей совершенствования процесса изучения алгебры и начал математического анализа ведется много лет. Исследования проводятся в разных направлениях, среди которых можно выделить следующие:
- усиление прикладной направленности обучения и упрощение некоторых логических моментов в курсе математического анализа базовой школы;
- изменение методики изучения основных понятий математического анализа на основе моделирования некоторых непрерывных процессов;
- совершенствование системы упражнений путем дополнения ее эвристическими задачами;
- решение проблем индивидуализации и дифференциации обучения;
- методические особенности применения пакета прикладных программ в обучении математике;
- проблемы компьютеризации при обучении математике;
- формирование исследовательских навыков у старшеклассников и другие.
Решению названных вопросов посвящены исследования В.В.Анисимова, Е.Г. Глаголевой, Л.О. Денищевой, А.Н. Землякова, В. И. Казиева, Н.Р. Колмаковой, С.А. Моркина, М.И. Немытовой, Л. С. Нураковой, И.Ф. Соколовского, Г.В. Токмазова, Г.С. Шевченко и многих других ученых.
Наличие многочисленных исследований по этим направлениям не случайно, поскольку подготовить выпускников к жизни в динамичном мире - значит вооружить их необходимыми знаниями, способами овладения ими. Умение учиться не возникает само собой, как следствие дополнительных педагогических требований, оно становиться результатом серьезной работы не только педагогов, но и самих учащихся.
Поиск решения проблемы - как создать условия для того, чтобы каждый ученик в условиях дифференциации обучения, изучил курс математики в том объеме, который ему необходим - привел нас к необходимости нахождения одного из решений вопроса, связанного с использованием компьютера в старших классах.
Необходимость изучения множества действительных чисел в средней школе вызвана потребностями курса. Изучением множества действительных чисел завершается рассмотрение числовых систем в школьном курсе. Понятие действительного числа лежит в основе метрической геометрии и измерения геометрических величин. Без понятия действительного числа нельзя четко определить понятие предела числовой последовательности и функции. Иными словами нельзя ввести начала математического анализа.
Основной целью изучения темы «Действительные числа» является: обобщение и систематизация полученных учащимися ранее знаний о рациональных и иррациональных числах. Дополнительные цели, способствующие достижению основной цели:
- обоснование арифметических операций над действительными числами, опираясь на определение иррациональных чисел как бесконечных непериодических десятичных дробей;
- введение понятия мощности бесконечных множеств действительных чисел, понятия замкнутости числового множества относительно некоторой операции;
- введение отношения порядка на множестве действительных чисел и рассмотрение доказательства известных ранее свойств числовых неравенств;
- знакомство с понятием погрешности приближения, методом оценки погрешности, использованием приближенных формул;
- развитие навыков работы с квадратными корнями;
- приведение доказательства правил извлечения квадратного корня из произведения, дроби и степени.
Актуальность темы исследования обусловлена тем, что полного обобщения понятия множества действительных чисел как числовой системы нет, что негативно влияет на дальнейшее построение курса. Поэтому необходимо разработать методику обучения темы «Действительные числа», в чем и заключается цель данной работы.
Объект исследования – процесс обучения алгебре и началам математического анализа в среднем общем образовании.
Предметом исследования является методика проведения уроков по предмету «Алгебра и начала математического анализа» для 10 класса по теме: «Действительные числа».
Цель исследования – разработка методического кейса по предмету «Алгебра и начала математического анализа» для 10 класса по теме: «Действительные числа».
Для достижения поставленной цели необходимо решить следующий комплекс задач:
изучить структуру современного урока и проблему методического обеспечения уроков предмета «Алгебра и начала математического анализа» в педагогической и методической литературе;
проанализировать требования учебной программы к уровню знаний и умений учащихся 10 классов по теме: «Действительные числа»;
разработать цикл уроков для 10 класса по теме: «Действительные числа».
Методы исследования:
- анализ литературы и материалов сети Интернет по проблеме исследования;
- систематизация и теоретическое обобщение;
- диагностические методы (беседа, наблюдение);
- современные программные средства и информационные технологии.
1.ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРЕПОДАВАНИЯ ПРЕДМЕТА «АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА»
1.1. Цели изучения предмета «Алгебра и начала математического анализа»
Изучение курса алгебры и начала математического анализа математики среднего общего образования направлено на достижение следующих целей:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин, для получения образования в областях, требующих углубленной математической подготовки;
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
воспитание культуры личности средствами математики, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей. Изучение алгебры и начал математического анализа по данной программе способствует формированию у учащихся личностных, метапредметных, предметных результатов обучения, соответствующих требованиям государственного образовательного стандарта среднего общего образования.
Личностные результаты:
1) воспитание гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;
2) формирование мировоззрения, соответствующего современному уровню развития науки и общественной практики;
3) ответственное отношение к обучению, готовность и способность к саморазвитию и самообразованию на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;
4) осознанный выбор будущей профессиональной деятельности на базе ориентирования в мире профессий и профессиональных предпочтений; отношение к профессиональной деятельности как к возможности участия в решении личных, общественных, государственных и общенациональных проблем; формирование уважительного отношения к труду, развитие опыта участия в социально значимом труде;
5) умение контролировать, оценивать и анализировать процесс и результат учебной и математической деятельности;
6) умение управлять своей познавательной деятельностью;
7) умение взаимодействовать с одноклассниками, детьми младшего возраста и взрослыми в образовательной, общественно-полезной, учебно-исследовательской, проектной и других видах деятельности;
8) критичность мышления, инициатива, находчивость, активность при решении математических задач.
Метапредметные результаты:
1) умение самостоятельно определять цели своей деятельности, ставить и формулировать для себя новые задачи в обучении;
2) умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;
3) умение самостоятельно принимать решения, проводить анализ своей деятельности, применять различные методы познания;
4) владение основными приемами познавательной, учебно-исследовательской
и проектной деятельности;
5) формирование понятийного аппарата, умения создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;
6) умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключения (индуктивное, дедуктивное и по аналогии) и делать выводы;
7) формирование компетентности в области использования информационно-коммуникационных технологий;
8) умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
9) умение самостоятельно осуществлять поиск в различных источниках, отбор, анализ, систематизацию и классификацию информации, необходимой для решения математических проблем, представлять её в понятной форме; принимать решение в условиях неполной или избыточной, точной или вероятностной информации; критически оценивать и интерпретировать информацию, получаемую из различных источников;
10) умение использовать математические средства наглядности (графики, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
11) умение выдвигать гипотезы при решении задачи, понимать необходимость их проверки;
12) понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Предметные результаты:
1) осознание значения математики для повседневной жизни человека;
2) представление о математической науке как сфере математической деятельности, об этапах её развития, о её значимости для развития цивилизации;
3) умение описывать явления реального мира на математическом языке; представление о математических понятиях и математических моделях как о важнейшем инструментарии, позволяющем описывать и изучать разные процессы и явления;
4) представление об основных понятиях, идеях и методах алгебры и математического анализа;
5) представление о процессах и явлениях, имеющих вероятностный характер, о статистических закономерностях в реальном мире, об основных понятиях элементарной теории вероятностей; умение находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;
6) владение методами доказательств и алгоритмов решения; умение их применять, проводить доказательные рассуждения в ходе решения задач;
7) практически значимые математические умения и навыки, способность их применения к решению математических и нематематических задач, предполагающие умения:
выполнять вычисления с действительными и комплексными числами;
решать рациональные, иррациональные, показательные, логарифмические, степенные и тригонометрические уравнения, неравенства, системы уравнений и неравенств;
решать текстовые задачи арифметическим способом, с помощью составления и решения уравнений, систем уравнений и неравенств;
решать текстовые задачи арифметическим способом, с помощью составления и решения уравнений, систем уравнений и неравенств;
использовать алгебраический «язык» для описания предметов окружающего мира и создания соответствующих математических
моделей;
выполнять тождественные преобразования рациональных, иррациональных, показательных, логарифмических, степенных, тригонометрических выражений;
выполнять операции над множествами;
исследовать функции с помощью производной и строить их графики;
вычислять площади фигур и объёмы тел с помощью определённого интеграла;
проводить вычисление статистических характеристик, выполнять приближённые вычисления;
решать комбинаторные задачи.
8) владение навыками использования компьютерных программ при решении математических задач.
1.2. Содержание темы «Действительные числа»
Множества. Операции над множествами. Целые и рациональные числа. Действительные числа. Бесконечно убывающая геометрическая прогрессия. Арифметический корень натуральной степени. Степень с рациональным и действительным показателями.
Основная цель – обобщить и систематизировать знания о действительных числах; сформировать понятие степени с действительным показателем; научить применять определения арифметического корня и степени, а также их свойства при выполнении вычислений и преобразовании выражений.
Необходимость расширения множества натуральных чисел до действительных мотивируется возможностью выполнять действия, обратные сложению, умножению и возведению в степень, а значит, возможностью решать уравнения вида:  .
.
Рассмотренный в начале темы способ обращения бесконечной периодической десятичной дроби в обыкновенную обосновывается свойствами сходящихся числовых рядов, в частности, нахождением суммы бесконечно убывающей геометрической прогрессии.
Действия над иррациональными числами строго не определяются, а заменяются действиями над их приближенными значениями − рациональными числами.
В связи с рассмотрением последовательных рациональных приближений иррационального числа, а затем и степени с иррациональным показателем на интуитивном уровне вводится понятие предела последовательности.
Арифметический корень натуральной степени 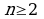 из неотрицательного числа и его свойства излагаются традиционно. Учащиеся должны уметь вычислять значения корня с помощью определения и свойств и выполнять преобразования выражений, содержащих корни.
из неотрицательного числа и его свойства излагаются традиционно. Учащиеся должны уметь вычислять значения корня с помощью определения и свойств и выполнять преобразования выражений, содержащих корни.
Степень с иррациональным показателем поясняется на конкретном примере: число 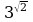 рассматривается как последовательность рациональных приближений
рассматривается как последовательность рациональных приближений 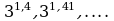 . Здесь же формулируются свойства степени с действительным показателем, которые будут использоваться при решении уравнений, неравенств, исследовании функций. 2 «РАЗРАБОТКА МЕТОДИЧЕСКОГО ОБЕСПЕЧЕНИЯ ПРЕПОДАВАНИЯ ТЕМЫ «ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА» ПРЕДМЕТА «АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА» В 10 КЛАССЕ
. Здесь же формулируются свойства степени с действительным показателем, которые будут использоваться при решении уравнений, неравенств, исследовании функций. 2 «РАЗРАБОТКА МЕТОДИЧЕСКОГО ОБЕСПЕЧЕНИЯ ПРЕПОДАВАНИЯ ТЕМЫ «ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА» ПРЕДМЕТА «АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА» В 10 КЛАССЕ
Целью данной работы является подготовка учебно-методических материалов по Алгебре и началам анализа для 10-х классов, необходимых для реализации примерной основной образовательной программы основного общего образования предмета «Алгебра и начала математического анализа. 10-11 кл. (базовый, профильный уровни)» / сост. Скафа Е.И., Федченко Л.Я., Полищук И.В. – 4-е изд. перераб., дополн. – ГОУ ДПО «ДонРИДПО». – Донецк: Истоки, 2020. – 38 с.» в 10 классе.
В данной работе разработан комплекс, включающий в себя, конспекты уроков, электронные презентации и задания для самостоятельных и контрольных работ для каждого урока Алгебры и начал математического анализа в 10 классе по теме: «Действительные числа».
Данная разработка составлена в соответствии с Примерной основной образовательной программой по учебному предмету «Алгебра и начала математического анализа. 10-11 кл. (базовый, профильный уровни)» / сост. Скафа Е.И., Федченко Л.Я., Полищук И.В. – 4-е изд. перераб., дополн. – ГОУ ДПО «ДонРИДПО». – Донецк: Истоки, 2020. – 38 с. и полностью соответствует календарно-тематическому планированию курса «Алгебра и начла математического анализа» (базовый компонент) [4].
Представленные методические разработки – это пособие, которое практически и теоретически раскрывает применяемую программу, методы и средства обучения, современные технологии в соответствии с темой и возрастными психолого-физиологическими особенностями учащихся. Разработки соответствуют выбранной теме «Действительные числа» и в полной мере раскрывают поставленные цели уроков. Работы имеют новизну, являются актуальными. В методических разработках использованы эффективные способы обучения, методические приемы, которые способствуют достижению целей уроков. Так, для актуализации знаний учащихся использованы облака слов, кроссворды, ребусы; при закреплении нового материала – групповая работа на отработку навыков действий с числами, преобразования чисел; для проверки полученных знаний – тестовая форма, самостоятельная работа в тетради, работа с файликом.
Визуализация материала реализована с помощью электронных презентаций.
Планируемые результаты освоения учащимися учебного материала по теме «Действительные числа»
Учащийся научится:
оперировать на базовом уровне понятиями:
целое число, делимость чисел, обыкновенная дробь, десятичная дробь, рациональное число, приближённое значение числа, часть, доля, отношение, процент, повышение и понижение на заданное число процентов, масштаб;
выполнять арифметические действия с целыми и рациональными числами;
выполнять несложные преобразования числовых выражений, содержащих степени чисел, либо корни из чисел;
сравнивать рациональные числа между собой;
оценивать и сравнивать с рациональными числами значения целых степеней чисел, корней натуральной степени из чисел;
изображать точками на числовой прямой целые и рациональные числа;
выполнять несложные преобразования целых и дробно-рациональных буквенных выражений;
Учащийся получит возможность:
свободно оперировать понятиями: целое число, делимость чисел, обыкновенная дробь, десятичная дробь, рациональное число, приближённое значение числа, часть, доля, отношение, процент, повышение и понижение на заданное число процентов, масштаб;
приводить примеры чисел с заданными свойствами делимости;
выполнять арифметические действия, сочетая устные и письменные приемы, применяя при необходимости вычислительные устройства;
проводить по известным формулам и правилам преобразования буквенных выражений;
находить значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
Учебный материал, связанный с понятием действительных чисел, не самый простой для восприятия школьника, требует особого внимания и труда от учителя. Для эффективного усвоения этого материала учащимися необходима четкая, логически обоснованная система тщательно подобранной теоретической информации, включающая наглядные примеры и практические задания, которых в вышеуказанных современных учебниках нет или содержится недостаточное количество. При этом следует учесть, что программа предмета «Алгебра и начала анализа» 10–11-х классов содержит значительное количество нового материала. Выделить дополнительное время для обобщения информации о числах учителю достаточно непросто.
В школьной программе изучаются иррациональные числа π и e, что, казалось бы, должно способствовать лучшему усвоению иррациональных чисел, иллюстрировать их наличие и применение в математике. Число π появляется при изучении окружности в курсе планиметрии и используется в формулах, связанных с окружностью, а в курсе стереометрии — при вычислении площади поверхности и объема тел вращения. Как правило, выпускники помнят, что π является постоянной величиной, выражающей отношение длины окружности к диаметру, помнят и умеют использовать формулы, в которых есть это число. Но наличие числа e в школьных учебниках для учащихся практически необъяснимо: оно появляется либо как основание показательной функции, значение производной (тангенс угла наклона касательной) которой в точке x0 = 0 равно 1 [3; 8], либо как основание при определении натурального логарифма, необходимость наличия которого в школьной программе тоже не вполне очевидна. Поскольку, как правило, второй замечательный предел не изучается в курсе предмета «Алгебра и начала анализа» общеобразовательной школы, число e чаще всего остается в памяти школьников лишь как основание показательной функции y = ex, производная которой совпадает с исходной функцией. Знание этого факта не добавляет ничего нового к пониманию, что такое иррациональные числа. Из вышесказанного следует сделать вывод: содержание учебного материала и отведенное количество часов на изучение действительных чисел в современных учебниках для общеобразовательной школы не способствуют глубокому и четкому усвоению понятий иррациональных и действительных чисел, развитию умений работать с числовыми множествами, правильному представлению о разных видах чисел.
Для преодоления этих трудностей учителю следует помнить, что задания используемые на уроках могут иметь различную сложность реализации, но все должны быть построены по одной дидактической схеме.
Принято выделять следующие основные типы уроков:
урок изучения нового материала;
уроки развития и закрепления умений и навыков;
урок контроля знаний;
обобщающий урок;
комбинированный урок.
Качество любого урока в значительной мере определяется тщательностью подготовки к нему учителя. Подготовку учителя к уроку схематично можно представить следующим образом.
1-й этап − изучение учебной программы. При этом особое внимание обращают на основные цели и задачи учебного предмета в целом и на цели и задачи, стоящие перед каждой учебной темой. Готовясь к изучению с учащимися очередной темы, учитель вновь обратится к программе, для того чтобы четко поставить перед собой цели и задачи, которые необходимо достигнуть и решить в процессе изучения темы в целом и на каждом конкретном уроке. Изучая содержание конкретной учебной темы, учитель уяснит логическую взаимосвязь учебного материала с ранее изученным, а также с материалом, который предстоит изучить позже. Это позволит более глубоко и четко сформулировать ближние и дальние цели изучения учебного материала.
2-й этап − изучение методической литературы. Изучив содержание очередной учебной темы по программе, учитель просматривает соответствующие разделы стабильного учебника, методических руководств и статьи в методических журналах, собирает материал для общего плана изучения темы (тематическое планирование). Тематический план не должен быть громоздким. В нем предусматривается самое важное и существенное, а именно: разбивка учебного материала по урокам, логическая взаимосвязь материала, календарные сроки проведения уроков (по неделям).
3-й этап − изучение материала конкретного урока в стабильном учебнике. Изучая учебник, учитель мысленно соотносит характер и логику изложения в нем учебного материала с достигнутым уровнем подготовки и уровнем развития своих учеников. Особенно большое внимание он уделяет доступности изложения учебного материала, отмечает то, что в учебнике изложено просто и доступно, с тем, чтобы часть материала поручить учащимся для самостоятельного изучения. Одновременно надо отметить и то, что может оказаться труднодоступным для учащихся. Особенно тщательно продумывается методика изложения этих вопросов на уроке.
4-й этап − изучение и подготовка имеющихся в школе средств обучения по теме урока. Учитель знакомится не только с имеющимися пособиями, просматривает учебные диафильмы и кинофильмы, но и с аннотациями учебных телевизионных передач, прослушивает звуковые пособия. Ничто так не подрывает авторитета учителя, как неудача в постановке учебного эксперимента. Определяя цели, непременно надо учитывать четыре возможные цели урока − усвоение знаний, привитие навыков и умений, развитие творческого опыта и воспитание. Цели следует обозначать конкретно в соответствии с темой, в зависимости от типа урока, но воспитательную надо иметь в виду всегда. Сообразно целям темы следует намечать упражнения, творческие задачи, конструируя их, если их нет в пособиях.
5-й этап − разработка плана урока. План урока − это конечный результат подготовительной работы учителя к проведению урока. План урока составляется на основе тематического плана с учетом реального продвижения в изучении темы.
В ходе выполнения выпускной работы для каждого урока разрабатывался:
План урока.
Презентация.
Раздаточный материал.
Интеллектуальная карта урока.
Выполнены следующие поурочные разработки по теме «Действительные числа»:
Урок 1. Целые и рациональные числа
Урок 2. Действительные числа
Урок 3. Действительные числа
Урок 4. Бесконечно убывающая геометрическая прогрессия
Урок 5. Бесконечно убывающая геометрическая прогрессия
Урок 6. Бесконечно убывающая геометрическая прогрессия
Урок 7. Арифметический корень натуральной степени
Урок 8. Арифметический корень натуральной степени
Урок 9. Степень с рациональным и действительным показателем
Урок 10. Степень с рациональным и действительным показателем
Урок 11.Решение задач
Урок 12. Решение задач
Урок 13.Контрольная работа
Урок 14.Анализ контрольной работы
Данный методический продукт предназначен как для начинающих педагогов, так и для учителей, имеющих большой опыт работы. Он позволяет эффективнее использовать время учителя как на уроке, так и при подготовке к уроку. В представленных далее разработках сделан акцент на практическое применение знаний учащихся, полученных в процессе обучения. Об этом свидетельствует подобранное большое количество практических упражнений на каждом уроке.
3. ПЛАНЫ-КОНСПЕКТЫ УРОКОВ ПО ПРЕДМЕТУ «АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА» ДЛЯ 10 КЛАССОВ ПО ТЕМЕ: «ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА»
ТЕМА 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА (14 часов)
Приведем примеры разработки трех конспектов уроков.
Урок № 1 Дата: ___ класс
Тема: ЦЕЛЫЕ И РАЦИОНАЛЬНЫЕ ЧИСЛА
Цели урока:
предметные – актуализировать знания о натуральных, целых, рациональных числах, овладение умением манипулировать с обыкновенными и десятичными дробями;
метапредметные – развитие умственных действий: анализ и синтез, сравнение, классификация, обобщение, формирование умения принимать и сохранять учебную цель и задачи, планировать собственную деятельность в соответствии с поставленной задачей и условиями её реализации, прогнозировать предстоящую работу, учить контролировать и оценивать свои действия, вносить коррективы в их выполнение на основе оценки и учёта характера ошибок, проявлять инициативу и самостоятельность в обучении.
личностные – создание условий для развития интереса к изучаемой теме; развитие самостоятельности, доброжелательного отношения, эмоциональной отзывчивости, формирование умения слушать и слышать собеседника, формировать умение сотрудничать с педагогом и сверстниками при решении учебных проблем, принимать на себя ответственность за результаты своих действий.
Задачи:
Закрепить изучаемый материал, меняя виды работы, по данной теме “Целые и рациональные числа”.
Развивать навыки и умения, в выполнении действий с десятичными и обыкновенными дробями, развивать логическое мышление, правильную и грамотную математическую речь, развитие самостоятельности и уверенности в своих знаниях и умениях при выполнении разных видов работ.
Воспитывать интерес к математике путём введения разных видов закрепления материала: устной работой, работой с учебником, работой у доски, ответами на вопросы и умением делать самоанализ, самостоятельной работой; стимулированием и поощрением деятельности учащихся.
Тип урока: Изучение нового материала.
Вид урока: изучение нового материала (беседа) с последующим закреплением через решение задач.
Методы и приемы обучения: объяснительно-иллюстративный; частично-поисковый; словесный (фронтальная беседа); наглядный (демонстрация компьютерной презентации); практический.
Средства обучения: авторская презентация; учебник (Алимов Ш.А. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10-11 классы: учеб. Для общеобразовательных организаций: базовый и углубленный уровень / Ш.А.Алимов, Ю.М. Колягин и др. – М.: Просвещение, 2016.); технические (компьютер, мультимедийный проектор).
План урока:
1.Организационный момент. (1 минута)
2. Актуализация знаний. (4 минуты)
3. Изложение нового материала. (13 минут)
4. Физкультминутка. (3 минуты)
5. Первичное закрепление (15 минут)
6. Проверка усвоения новых знаний. (5 минут)
7. Подведение итогов. (2 минуты)
8. Домашнее задание. (2 минуты)
ХОД УРОКА
Организационный момент.
1. Эмоциональный настрой и готовность учителя и обучающихся на урок. Сообщение цели и задач урока.
2. Организация рабочих мест:
- Проверьте ваши рабочие места: учебник, рабочая тетрадь, ручка.
Начинаем мы урок
Будем думать и решать!
На все вопросы отвечать,
Чтоб получить оценку «пять»
Мотивационное начало урока
Сегодня на уроке мы начинаем изучение новой главы «Действительные числа». Тема нашего урока – «Целые и рациональные числа».
Цель нашего урока – вспомнить и актуализировать наши знания о целых и рациональных числах.
![]() II. Актуализация знаний.
II. Актуализация знаний.
Фронтальный опрос
![]() (Слайд 2,3,4)
(Слайд 2,3,4)
- Какие числа называются натуральными?
(Для счета предметов используются числа, которые называются натуральными.)
- Как обозначается множество натуральных чисел?
(Для обозначения множества натуральных чисел употребляется буква 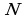 -
-
первая буква латинского слова Naturalis, «естественный», «натуральный»).
- Какие числа называются целыми и как обозначается это множество?
(Натуральные числа, числа им противоположные и число нуль, образуют множество целых чисел, которое обозначается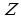 – первой буквой немецкого слова Zahl – «число»).
– первой буквой немецкого слова Zahl – «число»).
- Какие числа называются рациональными?
(Множество чисел, которое можно представить в виде 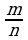 называется множеством рациональных чисел)
называется множеством рациональных чисел)
- Как обозначается множество рациональных чисел?
(Обозначается 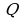 первой буквой французского слова Quotient – «отношение»)
первой буквой французского слова Quotient – «отношение»)

Устный счет

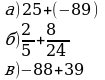
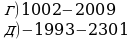
III. Изложение нового материала
![]() (Слайд 5)
(Слайд 5)
 Сформулируем определение целых и рациональных чисел и запишем его в тетради: (стр. 4).
Сформулируем определение целых и рациональных чисел и запишем его в тетради: (стр. 4).
Определение: Периодическая дробь – это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или группа цифр – период дроби.
Каждое рациональное число можно представить в виде бесконечной периодической десятичной дроби.
Например:
| Целое число | Конечная десятичная дробь | Бесконечная периодическая десятичная дробь |
|
|
|
|
| Период равен нулю | Период равен нулю | Период равен 2 |
![]() (Слайд 6)
(Слайд 6)
Работа с учебником![]()
Давайте рассмотрим задачу 1 на стр. 4.
Работа в группах (группы оформлены по рядам как сидит класс)
1-я группа – упражнение № 1(1)
2-я группа – упражнение №1 (5)
3-я группа – упражнение №1 (3)
IV. Физкультминутка
![]() Перед вами алгоритм для проведения физкультминутки. Давайте побудем немного исполнителями и постараемся точно выполнить все команды.
Перед вами алгоритм для проведения физкультминутки. Давайте побудем немного исполнителями и постараемся точно выполнить все команды.
Раз – подняться, подтянуться,
Два – согнуться, разогнуться,
Три – в ладоши три хлопка, головой три кивка
А четыре – руки шире,
Пять – руками помахать,
Шесть – за парты сесть опять.
V. Первичное закрепление
![]() (Слайд 7)
(Слайд 7)
№2. Выполните действия и запишите результат в виде десятичной дроби:
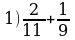
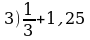
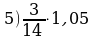
Ответы:
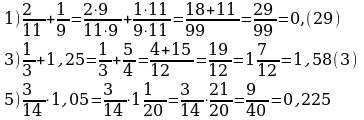
«Работа с файлом»
Предложить ученикам самостоятельно продумать и составить алгоритм перевода обыкновенной дроби в бесконечную периодическую дробь.
![]() (Слайд 8)
(Слайд 8)
Справедливо и обратное утверждение: каждая бесконечная периодическая десятичная дробь является рациональным числом.
Рассмотрим задачу 2 из параграфа и составим алгоритм : представить бесконечную периодическую десятичную дробь 0,2(18) в виде обыкновенной.
Пусть 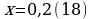 умножая на 10, получим
умножая на 10, получим 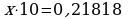
- нужно умножить дробь на 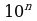 , где
, где 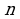 - количество десятичных знаков, содержащихся в записи этой дроби до периода. Получаем
- количество десятичных знаков, содержащихся в записи этой дроби до периода. Получаем 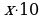 .
.
Умножая обе части последнего неравенства на 100, получим 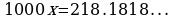
- нужно умножить дробь на 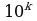 , где
, где 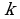 - количество цифр в периоде:
- количество цифр в периоде:
Получаем 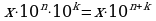
(2)-(1), получим 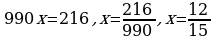
- отнять от равенства 2 равенство 1, решить полученное уравнение.
![]() (Слайд 9)
(Слайд 9)
№3(1) Записать в виде обыкновенной дроби бесконечную десятичную дробь:
1) 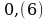
Решение
Пусть 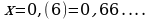
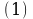
Период этой дроби состоит из одной цифры. Поэтому, умножая на обе части этого равенства на 10, находим
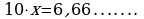
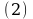
Вычитая из 2 равенство 1, получаем 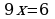 .
.
Отсюда 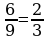 .
.
Ответ: 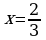
![]() (Слайд 10)
(Слайд 10)
3) 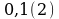
Решение
Пусть 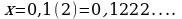
Так как в записи этого числа до периода содержится только один десятичный знак, то, умножая на 10, получаем
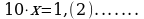 (1)
(1)
Период этой дроби состоит из одной цифры. Поэтому, умножая на обе части этого равенства на 10, находим
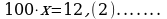
Вычитая из 2 равенство 1, получаем 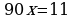 .
.
Отсюда 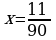
Ответ: 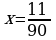
![]() (Слайд 11)
(Слайд 11)
5) 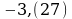
Решение
Пусть 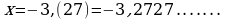
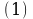
Период этой дроби состоит из двух цифр. Поэтому, умножая на обе части этого равенства на 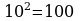 , находим
, находим
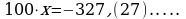 (2)
(2)
Вычитая из 2 равенство 1, получаем 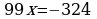 .
.
Отсюда 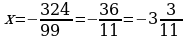
Ответ: 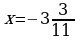
![]() (Слайд 12)
(Слайд 12)
6) 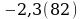
Решение
Пусть 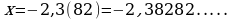
Так как в записи этого числа до периода содержится только один десятичный знак, то, умножая на 10, получаем
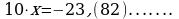
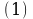
Период этой дроби состоит из двух цифр. Поэтому, умножая на обе части этого равенства на 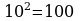 , находим
, находим
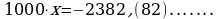
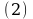
Вычитая из 2 равенство 1, получаем 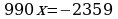 .
.
Отсюда 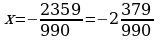
Ответ: 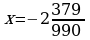
Дополнительно
№93 (стр. 35)Представить в виде обыкновенной дроби:
1) 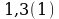
Решение
Пусть 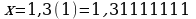
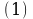
Так как в записи этого числа до периода содержится только один десятичный знак, то, умножая на 10, получаем

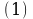
Период этой дроби состоит из двух цифр. Поэтому, умножая на обе части этого равенства на 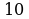 , находим
, находим
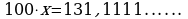
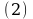
Вычитая из 2 равенство 1, получаем 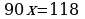 .
.
Отсюда 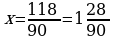
Ответ: 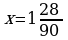
2) 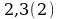
Решение
Пусть 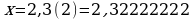
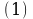
Так как в записи этого числа до периода содержится только один десятичный знак, то, умножая на 10, получаем
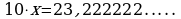
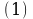
Период этой дроби состоит из двух цифр. Поэтому, умножая на обе части этого равенства на 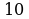 , находим
, находим
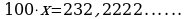
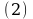
Вычитая из 2 равенство 1, получаем 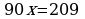 .
.
Отсюда 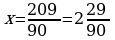
Ответ: 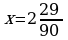
3) 
Решение
Пусть 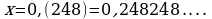
Так как в записи этого числа до периода содержится три десятичных знака, то, умножая на 10, получаем

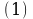
Период этой дроби состоит из двух цифр. Поэтому, умножая на обе части этого равенства на 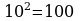 , находим
, находим
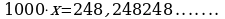
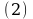
Вычитая из 2 равенство 1, получаем 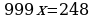 .
.
Отсюда 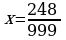
Ответ: 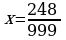
4) 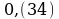
Решение
Пусть 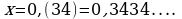
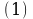
Так как в записи этого числа до периода содержится два десятичных знака, то, умножая на 100, получаем
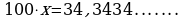
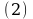
Вычитая из 2 равенство 1, получаем 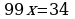 .
.
Отсюда 
Ответ: 
№ 92 (стр. 35) Вычислить
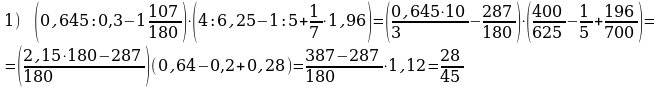
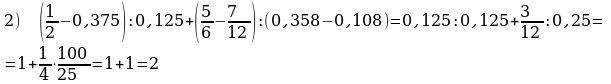
№ 5(1) Вычислить.
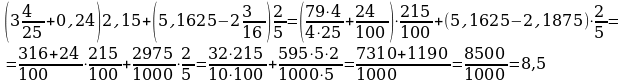
VI. Проверка усвоения новых знаний
Выполнение самостоятельно упражнения № 4 стр. 6. (по вариантам)
![]() (Слайд 13)
(Слайд 13)
Вариант 1
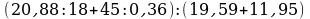
Решение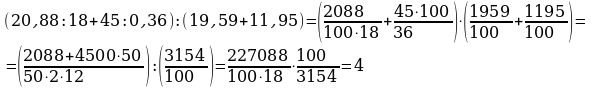
Вариант 2

Решение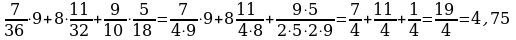
VII.Подведение итогов. Рефлексия
![]() (Слайд 14)
(Слайд 14)
Множества каких чисел вы знаете?
Приведите примеры этих чисел.
Что такое периодическая дробь?
Как записать её в виде обыкновенной?
У вас на парте есть карточки настроения, выберите подходящую карточку и вклейте в тетрадь.
|
|
|
|
VIII. Домашнее задание.
![]() (Слайд 15)
(Слайд 15)
1. §1, стр. 3 – 5, прочитать
2. № 1(2,4,6), № 2(2,4,6), № 3 (2,4), дополнительно (№ 5 (2))![]()
Урок № 6 Дата: ___ класс
Тема 6: БЕСКОНЕЧНО УБЫВАЮЩАЯ ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
Цели урока:
предметные – характеризуют умение и опыт обучающихся, которые приобретаются и закрепляются в процессе решения задач;
метапредметные – умение самостоятельно определять цели своего обучения, ставить для себя новые задачи, акцентировать мотивы и развивать интересы своей познавательной деятельности; умение планировать, контролировать и объективно оценивать свои учебные и практические действия в соответствии с поставленной задачей и условиями её реализации; самостоятельно оценивать уровень сложности заданий (упражнений) в соответствии с возможностями своего организма; формулировать, аргументировать и отстаивать своё мнение, умение вести дискуссию, обсуждать содержание и результаты совместной деятельности;
личностные – готовность и способность к саморазвитию и самообучению; готовность к личностному самоопределению; уважительное отношение к иному мнению; овладение навыками сотрудничества с взрослыми людьми и сверстниками; положительные качества личности и умение управлять своими эмоциями; дисциплинированность, внимательность, трудолюбие и упорство в достижении поставленных целей;
Задачи:
Закрепить изучаемый материал, меняя виды работы, по данной теме “Бесконечно убывающая геометрическая прогрессия”.
Развивать навыки и умения, в выполнении действий с десятичными и обыкновенными дробями, развивать логическое мышление, правильную и грамотную математическую речь, развитие самостоятельности и уверенности в своих знаниях и умениях при выполнении разных видов работ.
Воспитывать интерес к математике путём введения разных видов закрепления материала: устной работой, работой с учебником, работой у доски, ответами на вопросы и умением делать самоанализ, самостоятельной работой; стимулированием и поощрением деятельности учащихся.
Тип урока: урок развития и закрепления умений и навыков
Вид урока: решение задач.
Методы и приемы обучения: объяснительно-иллюстративный; частично-поисковый; словесный (фронтальная беседа); наглядный (демонстрация компьютерной презентации); практический.
Средства обучения: авторская презентация; учебник (Алимов Ш.А. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10-11 классы: учеб. Для общеобразовательных организаций: базовый и углубленный уровень / Ш.А.Алимов, Ю.М. Колягин и др. – М.: Просвещение, 2016.); технические , Алгебра и начала анализа. 10-11 классы: Учебно-методическое пособие / Сост. Потемкина Л.Л., Потемкин В.Л. – В 2-х ч. – Ч.1 – Донецк, 2017. – 130 с.), технические (компьютер, мультимедийный проектор).
План урока:
1.Организационный момент. (1 минута)
2. Актуализация знаний. (4 минуты)
3. Изложение нового материала. (13 минут)
4. Физкультминутка. (3 минуты)
5. Первичное закрепление (10 минут)
6. Проверка усвоения новых знаний. (5 минут)
7. Подведение итогов. (2 минуты)
8. Домашнее задание. (2 минуты)
ХОД УРОКА
Организационный момент.
1. Приветствие:
2. Организация рабочих мест:
- Проверьте ваши рабочие места: учебник, рабочая тетрадь, ручка.
Начинаем мы урок
Будем думать и решать!
На все вопросы отвечать,
Чтоб получить оценку «пять»
Мотивационное начало урока
Сегодня на уроке мы продолжаем изучение главы «Действительные числа». Тема нашего урока – «Бесконечно убывающая геометрическая прогрессия».
Цель нашего урока – расширение понятийной базы по теме и отработка навыков работы с прогрессиями.
Для достижения цели нашего урока, мы воспользуемся мультимедийной презентацией (приложение 1).
![]() . II. Актуализация знаний.
. II. Актуализация знаний.
Проверка домашнего задания
![]() (Слайд 2,3,4)
(Слайд 2,3,4)
Решение
№16 (2,4)
2) 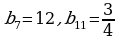
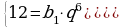
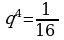
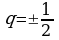
Т.к. 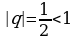 , то геометрическая прогрессия является бесконечно убывающей.
, то геометрическая прогрессия является бесконечно убывающей.
4) 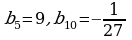
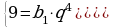
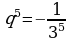
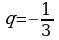
Так как 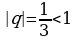 , то геометрическая прогрессия является бесконечно
, то геометрическая прогрессия является бесконечно
убывающей.
№21(2,4)
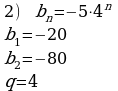
Т.к. 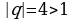 , то геометрическая прогрессия не является бесконечно убывающей.
, то геометрическая прогрессия не является бесконечно убывающей.
4) 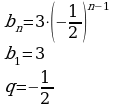
Т.к. 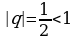 , то геометрическая прогрессия является бесконечно убывающей.
, то геометрическая прогрессия является бесконечно убывающей.
№ 24 (2)
2) 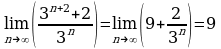
№ 22
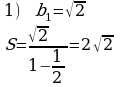
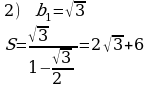
№ 25*
В заданной задаче чтобы найти высоту фигуры нужно сложить все стороны квадратов 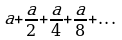 Найдем сумму геометрической прогрессии,
Найдем сумму геометрической прогрессии,
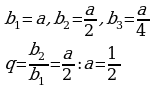
Т.к. 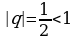 , то геометрическая прогрессия является бесконечно убывающая, следовательно сумма бесконечно убывающей геометрической прогрессии вычисляется по формуле
, то геометрическая прогрессия является бесконечно убывающая, следовательно сумма бесконечно убывающей геометрической прогрессии вычисляется по формуле 
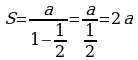
Фронтальный опрос (повторение)
![]() (Слайд 5,6)
(Слайд 5,6)
а) определения понятия геометрической прогрессии (ГП);
Геометрической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на постоянное для этой последовательности, отличное от нуля, число.
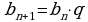 , где
, где 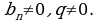
б) формулы n-ого члена ГП и знаменателя прогрессии;
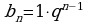 ,
,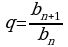
в) формула суммы n первых членов ГП.
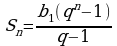 при
при 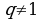
г) определение бесконечной геометрической прогрессии
Геометрическая прогрессия называется бесконечно убывающей, если модуль
её знаменателя меньше единицы.
д) формула суммы бесконечно убывающей геометрической прогрессии.

Математический диктант
№1. Найдите сумму первых пяти членов арифметической прогрессии, если её первый член равен 6 (1-й вариант), -20 (2-й вариант), а пятый член -6 (1-й вариант), 20 (2-й вариант).
№2. Найдите сумму первых пяти членов арифметической прогрессии, если её первый член равен -20(1-й вариант), 6 (2-й вариант), а разность равна 10(1-й вариант), -3(2-й вариант).
№3. Найдите сумму первых пяти членов геометрической прогрессии, если её первый член равен 1(1-й вариант), -1 (2-й вариант), а знаменатель равен -2(1-й вариант), 2(2-й вариант).
Решение
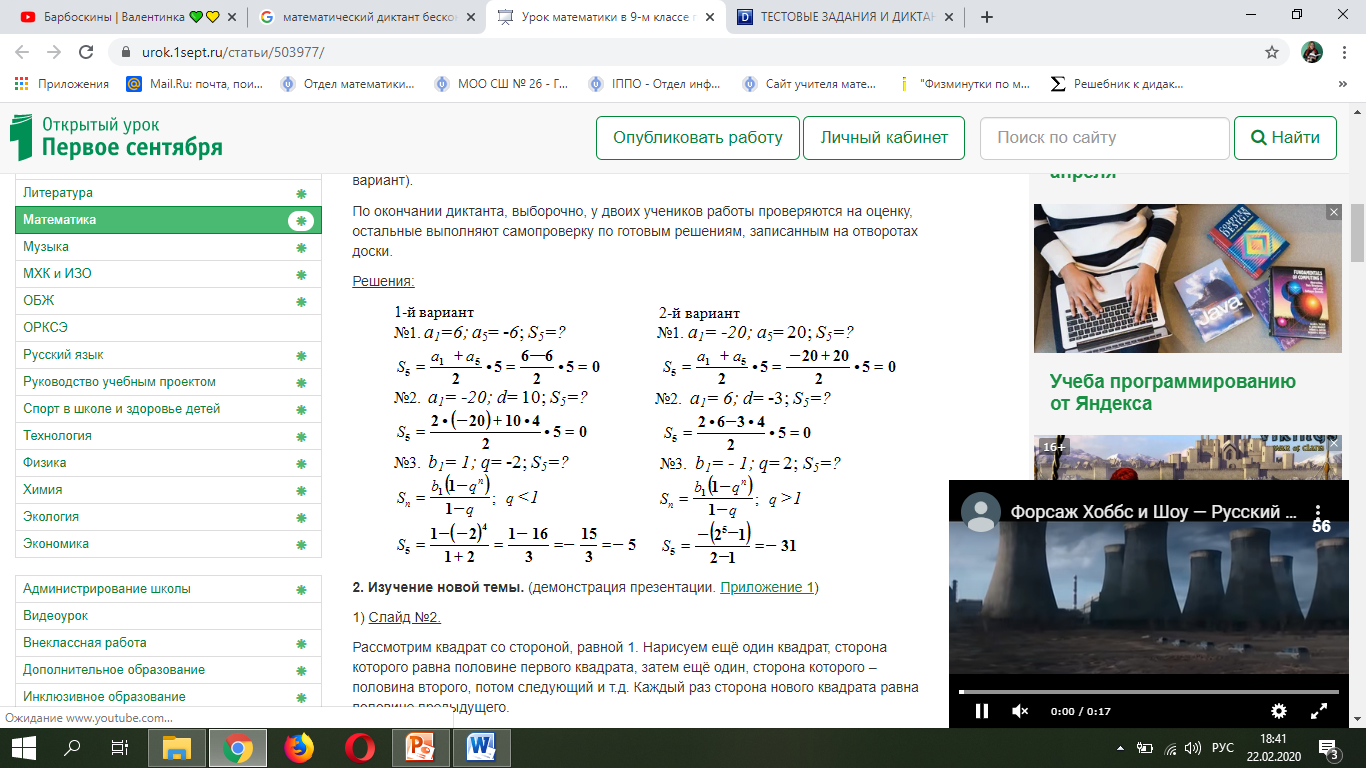
![]() (Слайд 7)
(Слайд 7)
III. Закреплениe и отработки навыков решения задач
![]() (Слайд 8,9)
(Слайд 8,9)
Работа с учебником![]()
Алимов Ш.А. Математика: алгебра и начала математического анализа дидактические маериалы. Алгебра и начала математического анализа. 10 класс: учеб. Для общеобразовательных организаций: базовый и углубленный уровень / Ш.А.Алимов, Ю.М. Колягин и др. – М.: Просвещение, 2016.
Стр. 33
Вариант 1
№ 1 Выяснить, является ли геометрической прогрессией последовательность, заданная формулой 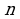 - го члена:
- го члена: 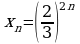
№2. Выяснить, является ли бесконечно убывающей геометрической прогрессией последовательность, заданная формулой 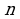 - го члена:
- го члена:
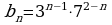
Найти сумму бесконечно убывающей геометрической прогрессии (3-5)
№ 3 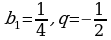
№ 4. 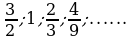
№ 5. 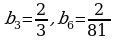
Записать бесконечную периодическую десятичную дробь в виде обыкновенной (6-8)
№ 6. 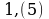
№ 7. 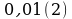
№ 8. 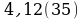
Вариант 2
№ 1. Выяснить, является ли геометрической прогрессией последовательность, заданная формулой 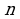 - го члена:
- го члена: 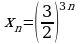
№2. Выяснить, является ли бесконечно убывающей геометрической прогрессией последовательность, заданная формулой 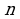 - го члена:
- го члена:
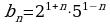
Найти сумму бесконечно убывающей геометрической прогрессии (3-5)
№ 3. 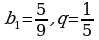
№ 4. 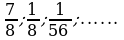
№ 5. 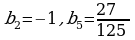
Записать бесконечную периодическую десятичную дробь в виде обыкновенной (6-8)
№ 6. 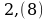
№ 7. 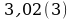
№ 8. 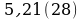
Решение
Вариант 1
1. заданная последовательность геометрическая прогрессия
2. последовательность является бесконечно убывающей геометрической прогрессией
3. 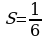
4. 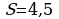
5. 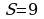
6. 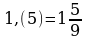
7. 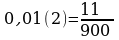
8. 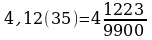
Вариант 2
1. заданная последовательность геометрическая прогрессия
2. последовательность является бесконечно убывающей геометрической прогрессией
3. 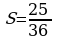
4. 
5. 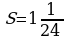
6. 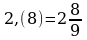
7. 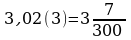
8. 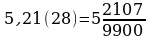
IV. Физкультминутка
![]() Перед вами алгоритм для проведения физкультминутки. Давайте побудем немного исполнителями и постараемся точно выполнить все команды.
Перед вами алгоритм для проведения физкультминутки. Давайте побудем немного исполнителями и постараемся точно выполнить все команды.
Перед нами дуб широкий, (Руки в стороны)
А над нами дуб высокий. (Руки вверх)
Вдруг над нами сосны, ели (Наклоны головой)
Головами зашумели (Хлопки)
Грянул гром, сосна упала, (Присели)
Только ветками качала. (Встали, покачали головой)
V. Проверка усвоения материала (тестирование).
Является ли геометрическая прогрессия бесконечно убывающей, если:
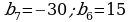 ?
?
Найдите сумму бесконечно убывающей геометрической прогрессии: -25; -5; -1;…
Записать бесконечную десятичную периодическую дробь 0,(9) в виде обыкновенной дроби.
Решение
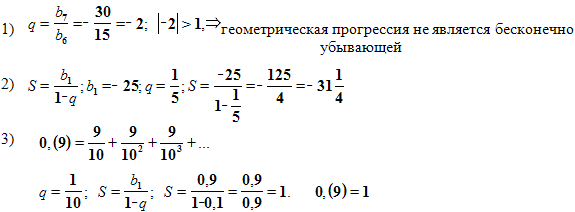
![]() Слайд (10) Ответы самостоятельной озвучивает учитель. После выполнения самостоятельной работы в тетради, ответы будут записаны на файлик, которым ученики обменяются и проверят друг друга.
Слайд (10) Ответы самостоятельной озвучивает учитель. После выполнения самостоятельной работы в тетради, ответы будут записаны на файлик, которым ученики обменяются и проверят друг друга.
VI.Подведение итогов. Рефлексия
У вас на парте есть карточки настроения, выберите подходящую карточку и вклейте в тетрадь.
|
|
|
|
VII. Домашнее задание.
1. Повторить правила и формулу из §3, стр. 11 – 15![]()
2. №26, 15, 13
Урок № 12 Дата: ___ класс
Тема: РЕШЕНИЕ ЗАДАЧ
Цели урока:
предметные – обобщение знаний по теме «Действительные числа», отработать навыки решения выражений содержащих корни, степени, бесконечно убывающие геометрические прогрессии; научить применять полученные знания при решении заданий, стимулировать учащихся к овладению приемами, которые будут полезны в дальнейшем;
метапредметные – развитие умственных действий: анализ и синтез, сравнение, классификация, обобщение, формирование умения принимать и сохранять учебную цель и задачи, планировать собственную деятельность в соответствии с поставленной задачей и условиями её реализации, прогнозировать предстоящую работу, учить контролировать и оценивать свои действия, вносить коррективы в их выполнение на основе оценки и учёта характера ошибок, проявлять инициативу и самостоятельность в обучении.
личностные – создание условий для развития интереса к изучаемой теме; развитие самостоятельности, доброжелательного отношения, эмоциональной отзывчивости, формирование умения слушать и слышать собеседника, формировать умение сотрудничать с педагогом и сверстниками при решении учебных проблем, принимать на себя ответственность за результаты своих действий.
Задачи:
обобщить понятия по теме «Действительные числа»; отработать умение находить значение выражений содержащих степени, корни, определять рациональные и иррациональные числа; закрепить умения использовать полученные знания при упрощении выражений; выработать навык использования полученных знаний;
интеллектуальное, эмоциональное, личностное развитие ученика; развивать умение обобщать, систематизировать на основе сравнения, делать вывод; активизировать самостоятельную деятельность; развивать познавательный интерес;
воспитание коммуникативной и информационной культуры обучающихся;
Тип урока: урок развития и закрепления умений и навыков
Вид урока: решение задач.
Методы и приемы обучения: объяснительно-иллюстративный; частично-поисковый; словесный (фронтальная беседа); наглядный (демонстрация компьютерной презентации); практический.
Средства обучения: авторская презентация; учебник (Алимов Ш.А. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10-11 классы: учеб. Для общеобразовательных организаций: базовый и углубленный уровень / Ш.А.Алимов, Ю.М. Колягин и др. – М.: Просвещение, 2016.); Алгебра и начала анализа. 10-11 классы: Учебно-методическое пособие / Сост. Потемкина Л.Л., Потемкин В.Л. – В 2-х ч. – Ч.1 – Донецк, 2017. – 130 с.), технические (компьютер, мультимедийный проектор).
План урока:
1.Организационный момент. (1 минута)
2. Актуализация знаний. (4 минуты)
3. Изложение нового материала. (13 минут)
4. Физкультминутка. (3 минуты)
5. Первичное закрепление (10 минут)
6. Проверка усвоения новых знаний. (5 минут)
7. Подведение итогов. (2 минуты)
8. Домашнее задание. (2 минуты)
ХОД УРОКА
I. Организационный момент.
1. Приветствие:
2. Организация рабочих мест:
- Проверьте ваши рабочие места: учебник, рабочая тетрадь, ручка.
Начинаем мы урок
Будем думать и решать!
На все вопросы отвечать,
Чтоб получить оценку «пять»
Мотивационное начало урока
Сегодня на уроке мы отрабатываем навыки работы с выражениями по теме «Действительные числа». Тема нашего урока – «Решение задач».
Цель нашего урока – отработать навыки решения выражений содержащие арифметические корни натуральной степени, степени с рациональными и действительными показателями, бесконечные периодические десятичные дроби.
Для достижения цели нашего урока, мы воспользуемся мультимедийной презентацией (приложение 1).
![]() . II. Актуализация знаний.
. II. Актуализация знаний.
![]() (Слайд 2)
(Слайд 2)
Проверка домашнего задания
Ответы
| № 83(2,4) 2) 4) №79(2) 2)3 №99(2,4) 2) 4) | № 97(2,4,6) 2)1,5 4) 1,5 6)4 № 115 1) 2) 3)1 4)
|
Фронтальный опрос
![]() (Слайд 3,4)
(Слайд 3,4)
- Какую дробь называют периодической?
(Периодическая дробь, это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или группа цифр – период дроби.)
- Какую прогрессию называют бесконечно убывающей?
(Геометрическая прогрессия называется бесконечно убывающей, если модуль ее знаменателя меньше единицы.)
- Свойства корней 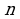 -степени.
-степени.
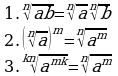
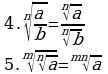
- Дайте определение степени с рациональным показателем.
Если 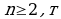 - целое число и частное
- целое число и частное  является целым числом, то при
является целым числом, то при 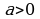 справедливо равенство
справедливо равенство 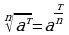
- Сформулируй определение степени с действительным показателем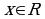 - натуральное число,
- натуральное число, 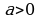 степень
степень 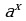 является положительным действительным числом:
является положительным действительным числом: 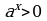 при
при 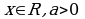 .
.
Математический диктант
![]() (Слайд 5)
(Слайд 5)
1. Запишите числа: 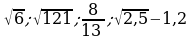 . Выпишите числа, которые принадлежат множеству иррациональных чисел.
. Выпишите числа, которые принадлежат множеству иррациональных чисел.
2. Округлите число 999,99 до десятых.
3. Вычислите: 
4.Можно ли представить дробь 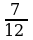 в виде конечной десятичной дроби?
в виде конечной десятичной дроби?
5. Сколько натуральных чисел находится на промежутке 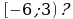
III. Закреплениe и отработки навыков решения задач
![]() (Слайд 6)
(Слайд 6)
Работа с учебником![]()
Выполняем упражнения № 106, 107, 108, 110, 111 (1,3), 112 (1,3,5,7), 113 (1), 114 (1,3), 117 (1,3),118
Ответы
№ 106
1) 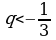 Прогрессия бесконечно убывающая
Прогрессия бесконечно убывающая
2) 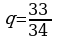 Прогрессия бесконечно убывающая
Прогрессия бесконечно убывающая
3) 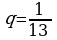 Прогрессия бесконечно убывающая
Прогрессия бесконечно убывающая
4) 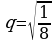 Прогрессия бесконечно убывающая
Прогрессия бесконечно убывающая
| № 107 1) 2) № 108
№ 110
№ 111 (1,3) 1) 3) № 113 (1) 1) 3 | № 112 (1,3,5,7) 1) 3) 5) 7) № 114 (1,3) 1) 3) № 117 (1,3) 1) 3) 1 |
№118
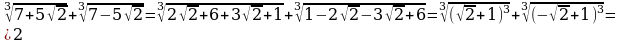
Из сборника Потемкиных стр. 65-66
11. Упростить выражения:
| 1. 3. 5. Ответ: 7. Ответ: 9. Ответ: | 2. 4. 6. Ответ: 8. Ответ: 10. Ответ: |
12. Упростить выражения:
| 1. 3. 5. 7. 9. 11. 13. 15. 17. Ответ: 19. 21. 23. Ответ: | 2. 4. 6. 8. 10. 12. 14. 16. 18. Ответ: 20. 22. 24.
|
IV. Физкультминутка
![]() Перед вами алгоритм для проведения физкультминутки. Давайте побудем немного исполнителями и постараемся точно выполнить все команды.
Перед вами алгоритм для проведения физкультминутки. Давайте побудем немного исполнителями и постараемся точно выполнить все команды.
Головою мы вращаем,
Будто твёрдо отвечаем:
«Нет, не буду, не хочу!»
Это детям по плечу.
(Вращение головой вправо и влево.)
V. Проверка знаний.
![]() (Слайд 7,8)
(Слайд 7,8)
В конце урока учитель соберет тетради для проверки самостоятельной работы.
(Из дидактических материалов к учебнику Шабунин 10 класс стр. 42)
Вариант 1
1. Вычислить:
1) 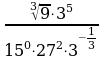 2)
2) 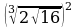
2. Известно, что 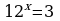 . Найти
. Найти 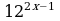
3. Выполнить действия (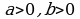 )
)
1) 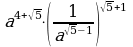 2)
2) 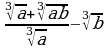
4.Сравнить числа
1) 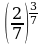 и
и 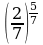 2)
2)  и
и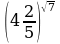
5. Записать бесконечную периодическую десятичную дробь  в виде обыкновенной.
в виде обыкновенной.
6. Упростить
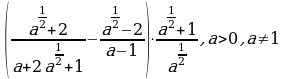
Вариант 2
1. Вычислить:
1) 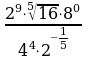 2)
2) 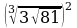
2. Известно, что 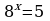 . Найти
. Найти 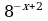
3. Выполнить действия (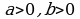 )
)
1) 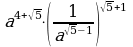 2)
2) 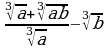
4.Сравнить числа
1) 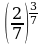 и
и 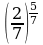 2)
2)  и
и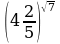
5. Записать бесконечную периодическую десятичную дробь  в виде обыкновенной.
в виде обыкновенной.
6. Упростить
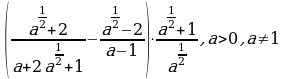
Ответы
| Вариант 1 №1 1)1 2) 4 №2 3,2 № 3 1) 2) 1 № 4 1) 2) № 5
№ 6
| Вариант 2 №1 1)4 2)9 №2 3,2 № 3 1) 2) -1 № 4 1) 2) № 5
№ 6
|
VII. Подведение итогов. Рефлексия
У вас на парте есть карточки настроения, выберите подходящую карточку и вклейте в тетрадь.
|
|
|
|
VIII. Домашнее задание.
1. § 2-5 повторить определения и свойства
2. Подготовиться к контрольной работе. Выполнить № 111 (2, 4), 112 (2,4,6,8), 113 (2), 114(2,4),117 (2,4).![]()
ВЫВОДЫ
Цель исследования достигнута. Разработан цикл уроков по предмету «Алгебра и начала математического анализа» для 10 класса по теме «Действительные числа».
Удалось установить следующее.
1. Применение современных образовательных технологий в методической работе преподавателя на уроках математики позволяет:
повысить у учителей применение информатики и ИКТ на уроках математики;
организовать работу учителей по самостоятельному овладению конкретными знаниями, необходимыми для применения их в практической деятельности;
формировать и развивать метапредметные и коммуникативные компетентности учителей;
совершенствовать методическую компетентность преподавателя;
оптимально сочетать в педагогическом процессе современные образовательные технологии с традиционным обучением.
Приведенные методы использования современных образовательных технологий как средства повышения мотивации к изучению математики посредством информационно-коммуникационных технологий в методической работе преподавателя могут существенно повысить эффективность образовательного процесса, решить стоящие перед образовательным учреждением задачи воспитания всесторонне развитой, творчески свободной личности.
Результаты работы достигнуты путем решения комплекса задач:
изучить структуру современного урока и проблему методического обеспечения уроков предмета «Алгебра и начала математического анализа» в педагогической и методической литературе;
проанализировать требования учебной программы к уровню знаний и умений учащихся 10 классов по теме: «Действительные числа»;
разработать цикл уроков для 10 класса по теме: «Действительные числа».
изучить структуру современного урока и проблему методического обеспечения уроков предмета «Алгебра и начала математического анализа» в педагогической и методической литературе;
проанализировать требования учебной программы к уровню знаний и умений учащихся 10 классов по теме: «Действительные числа»;
разработать цикл уроков для 10 класса по теме: «Действительные числа».
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
. Алгебра и начала математического анализа. 10 класс: базовый и профильный уровни / Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В М.: Просвещение, АО «Московские учебники», 2016. – 385 с.
Методика преподавания математики в средней школе. Частные методики / Колягин Ю.М., Луканкин Г.Л., Мокрушин Е.Л. и другие., М., Просвещение, 2015
Алгебра и начала анализа. 10 класс. 1 полугодие. Поурочные планы / Т.И. Купорова. - М.: Учитель, 2017. - 100 c
Алгебра и начала анализа. 10-11 класс / А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын, и др.. - М.: Просвещение; Издание 13-е, 2015. - 384 c
Алгебра и начала анализа. 10-11 классы. Тематические тесты к учебнику Ш. А. Алимова "Алгебра и начала анализа. 10-11 классы" / В.К. Шарапова. - М.: Феникс, 2007. – 384 с.
Алгебра и начала анализа: Учебник для 10-11 классов общеобразовательных учреждений / ред. А.Н. Колмогоров. - М.: Просвещение; Издание 15-е, 2015. – 384 с.
Государственный образовательный стандарт среднего общего образования Донецкой Народной Республики, утвержденный Приказом Министерства образования и науки Донецкой Народной Республики от 07.08.2020 г. № 121-НП.
Закон Донецкой Народной Республики «Об образовании», утвержденный Постановлением №I – 233П – НС Народного Совета Донецкой Народной Республики от 19 июня 2015 г.
Конституция Донецкой Народной Республики (С изменениями, внесенными Законами от 27.02.2015 года № 17-ІНС от 29.06.2015 года № 63-ІНС от 11.09.2015 года № 92-ІНС);
Математика : справочные материалы / В. А. Гусев, А. Г. Мордкович. – Москва : Просвещение, 2014. – 271 с
Методика преподавания математики в средней школе: Общая методика; Учебное пособие для студентов физико-математического факультета педагогических институтов / В.А. Оганесян, Ю.М. Колягин, Г.Л. Луканкин, В.Я. Саннинский, -2-е издание переработано и дополнено / Москва, Просвещение, 2016.
Новосельцева З.И. Развернутые планы лекций и учебные задания для студентов по курсу "Теоретические основы обучения математике"/ С.-Петербург, Изд-во "Образование", РГПУ, 2017
О совершенствовании методов обучения математике / Сост. B.C. Крамор.- Москва : Просвещение, 2017.- 160 с.
Общая методика преподавания математики в средней школе / Епишева О.Б., Тобольск, Изд-во ТГПИ им. Д.И. Менделеева, 2017, - 402 с.
Понтрягин Л.С. О математике и качестве её преподавания - Коммунист, 1980.
Примерная основная образовательная программа по учебному предмету «Алгебра и начала математического анализа. 10-11 кл. (базовый, профильный уровни)» / сост. Скафа Е.И., Федченко Л.Я., Полищук И.В. – 4-е изд. перераб., дополн. – ГОУ ДПО «ДонРИДПО». – Донецк: Истоки, 2020. – 38 с.
Проблемы электронного учебника / Смирнов А.Н., Математика в школе. 2018. - №5. - С. 15-16.
Рогановский Н.М. Методика преподавания математики в средней школе / Минск, Изд-во "Высшая школа", 2018
Теория и методика обучения математике : конструирование учебных заданий с элементами истории математики: учебно-методическое пособие /Д. В. Смолякова; МОиН РФ, ФГБОУ ВПО ТГПУ. – Томск: Издательство Томского государственного педагогического университета, 2015. – 49 с.





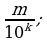 где
где 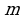 – целое число,
– целое число,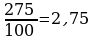
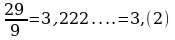




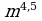
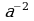
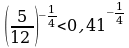
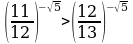
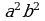
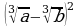
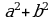
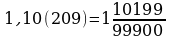
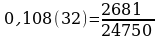
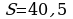
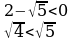
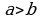
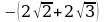
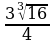
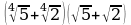
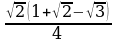
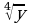
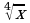

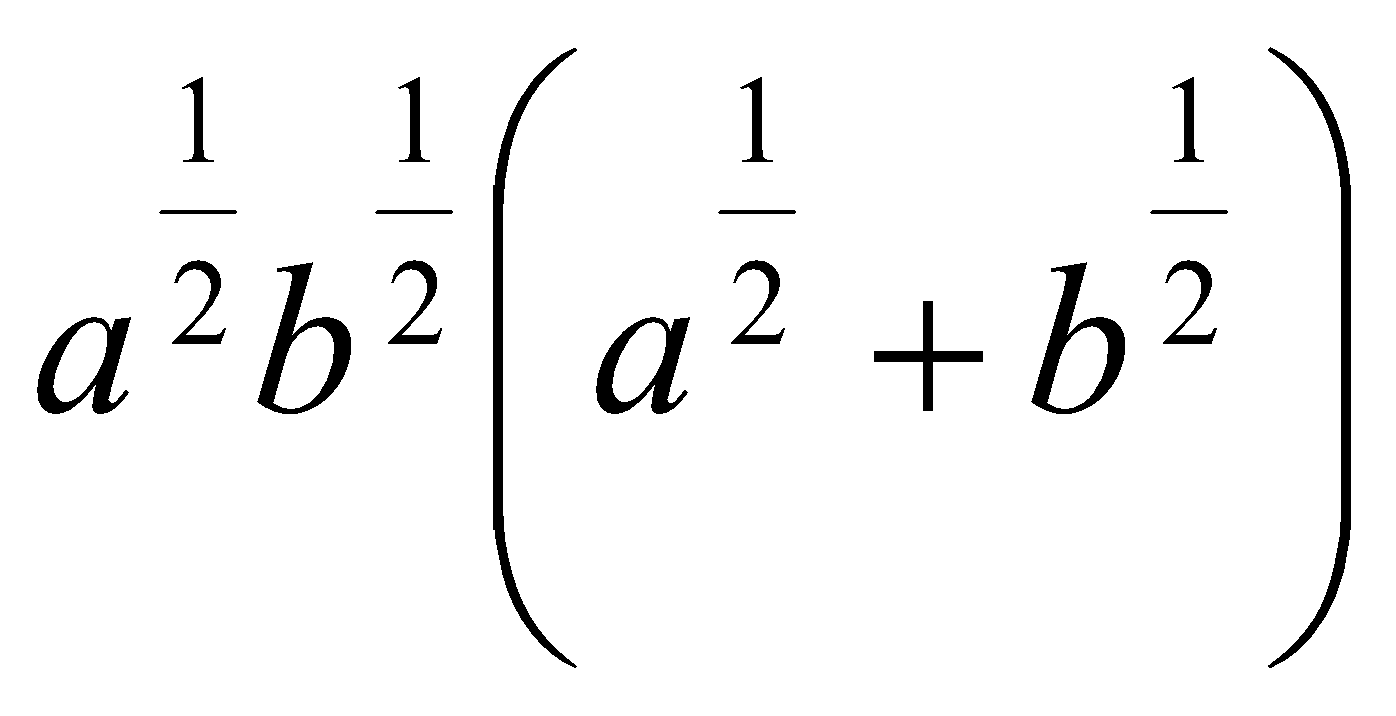 . Ответ:
. Ответ: 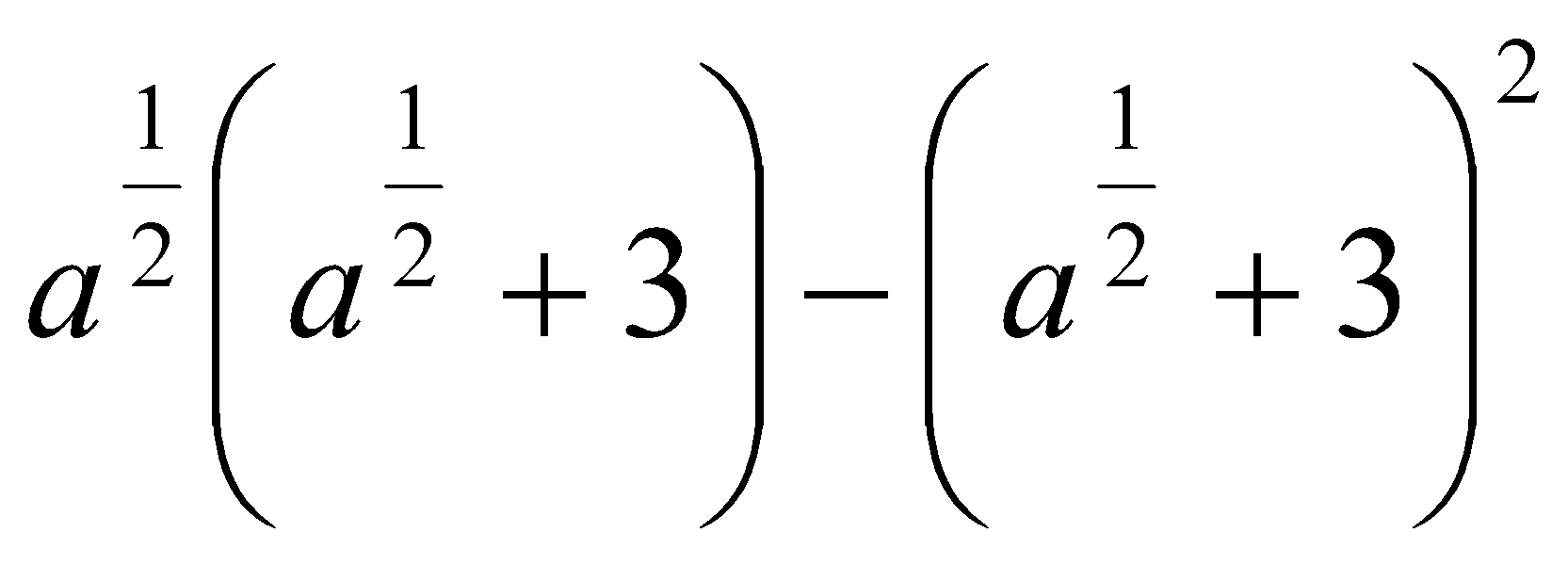 . Ответ:
. Ответ: 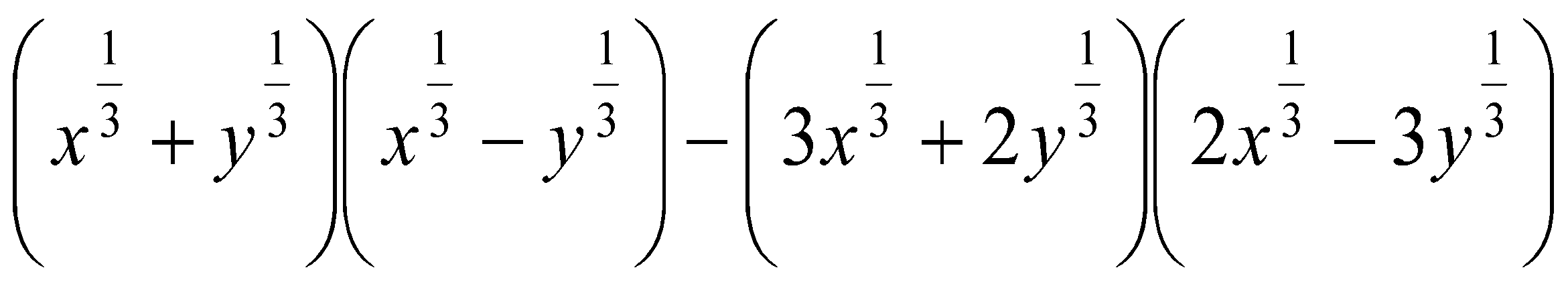 .
. 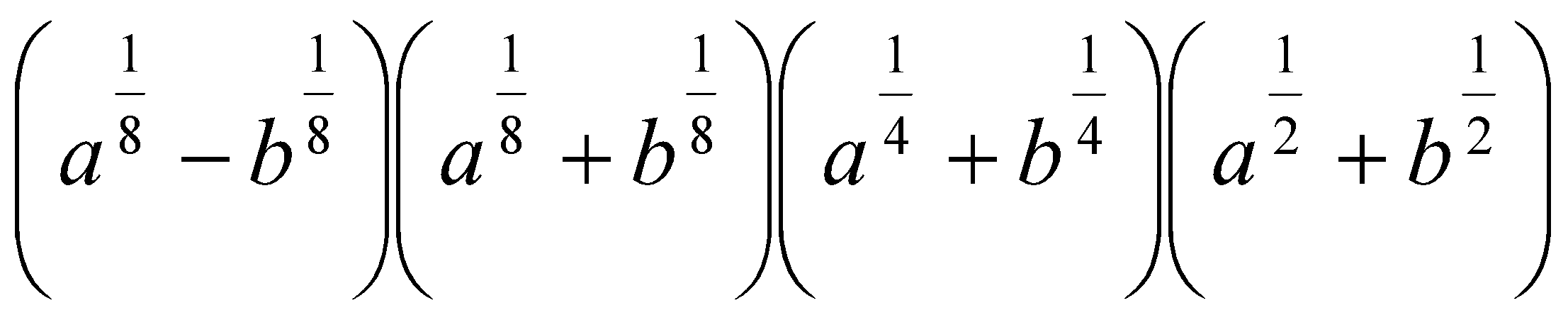 .
. 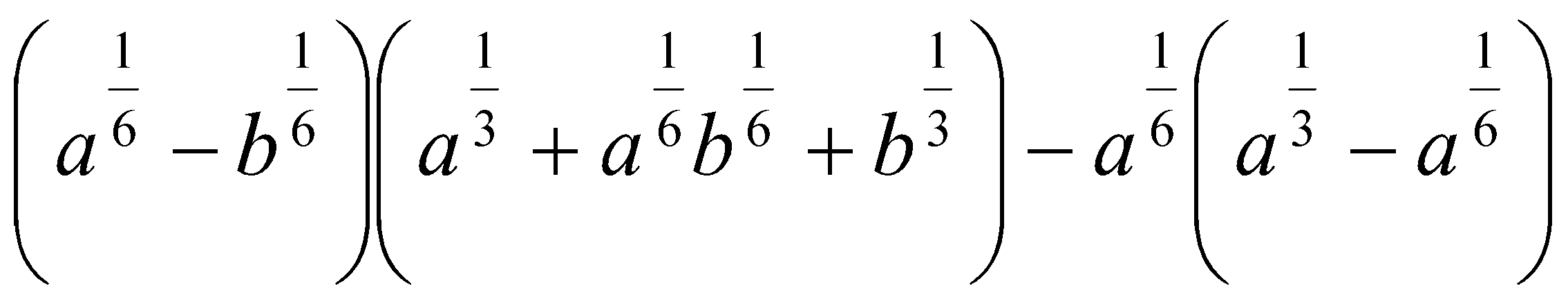 .
. 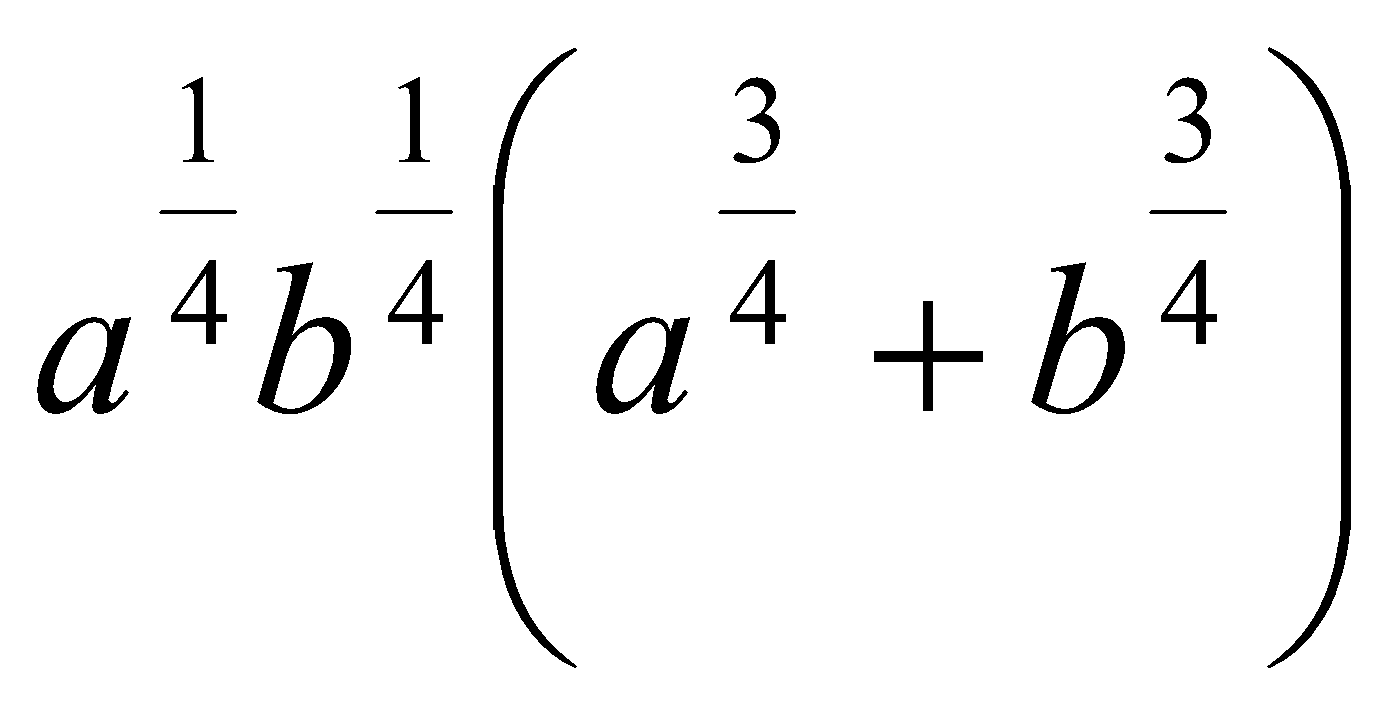 . Ответ:
. Ответ:  . Ответ:
. Ответ: 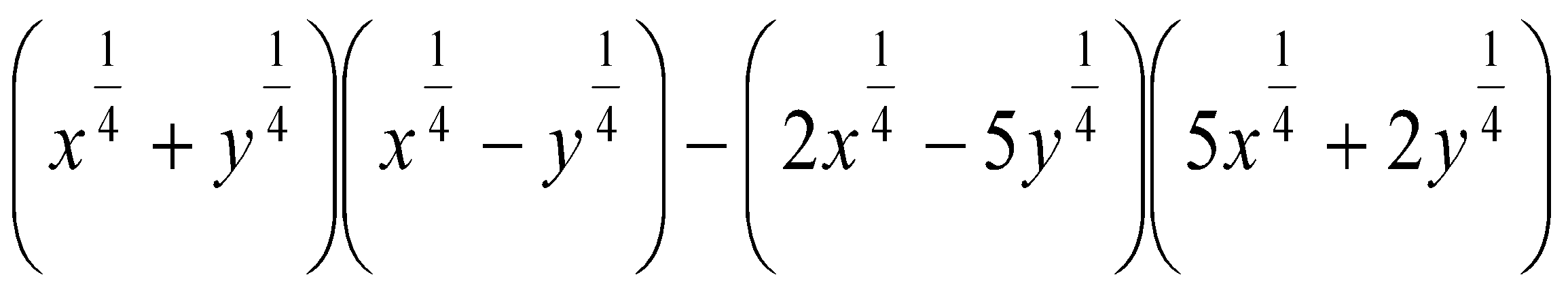 .
. 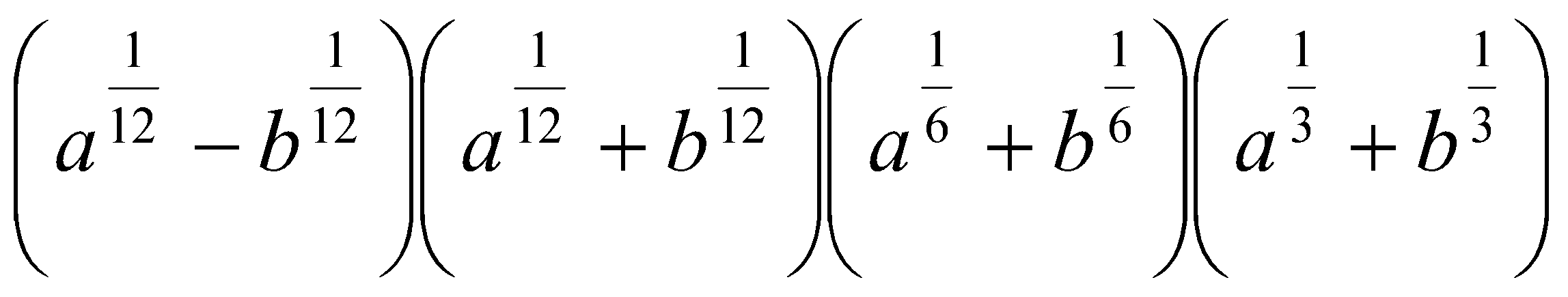 .
. 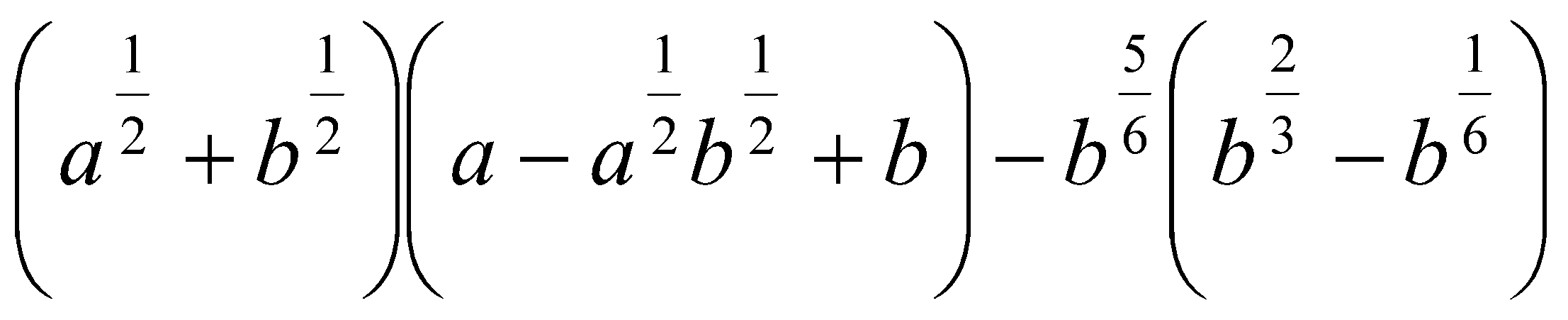 .
. 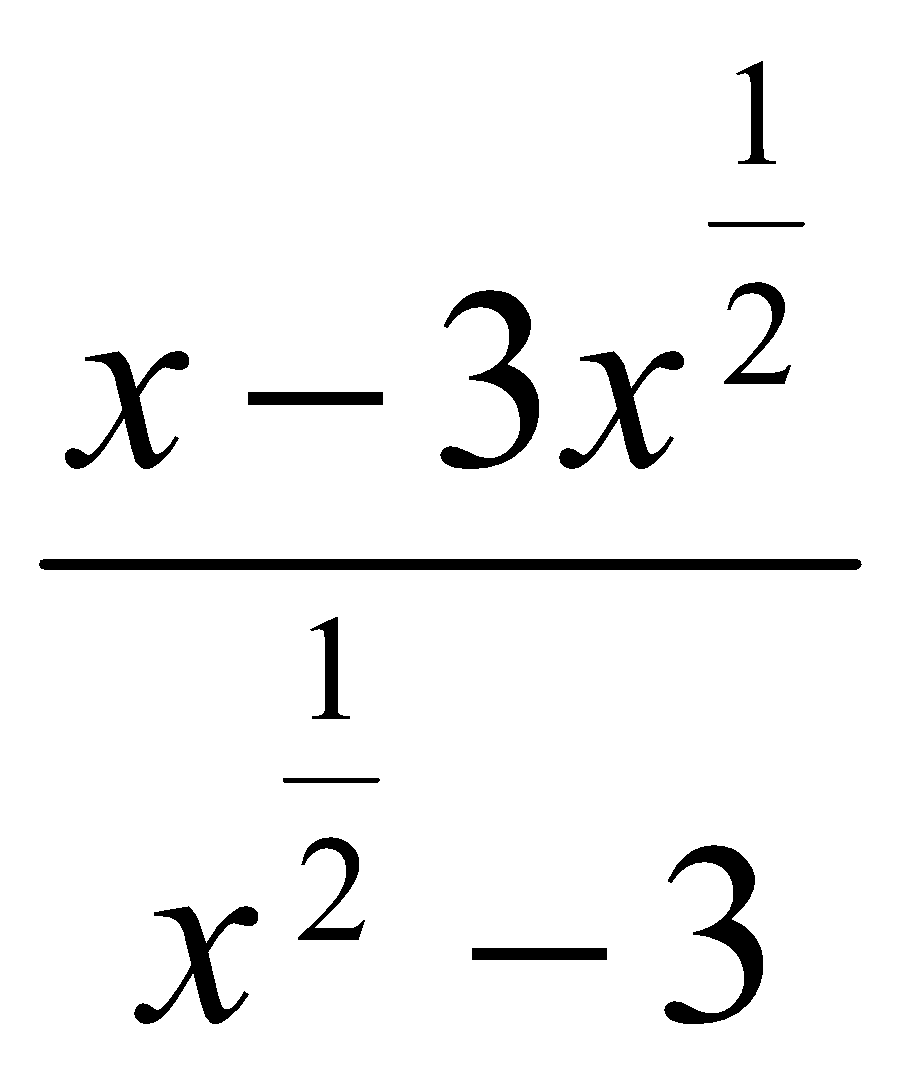 . Ответ:
. Ответ: 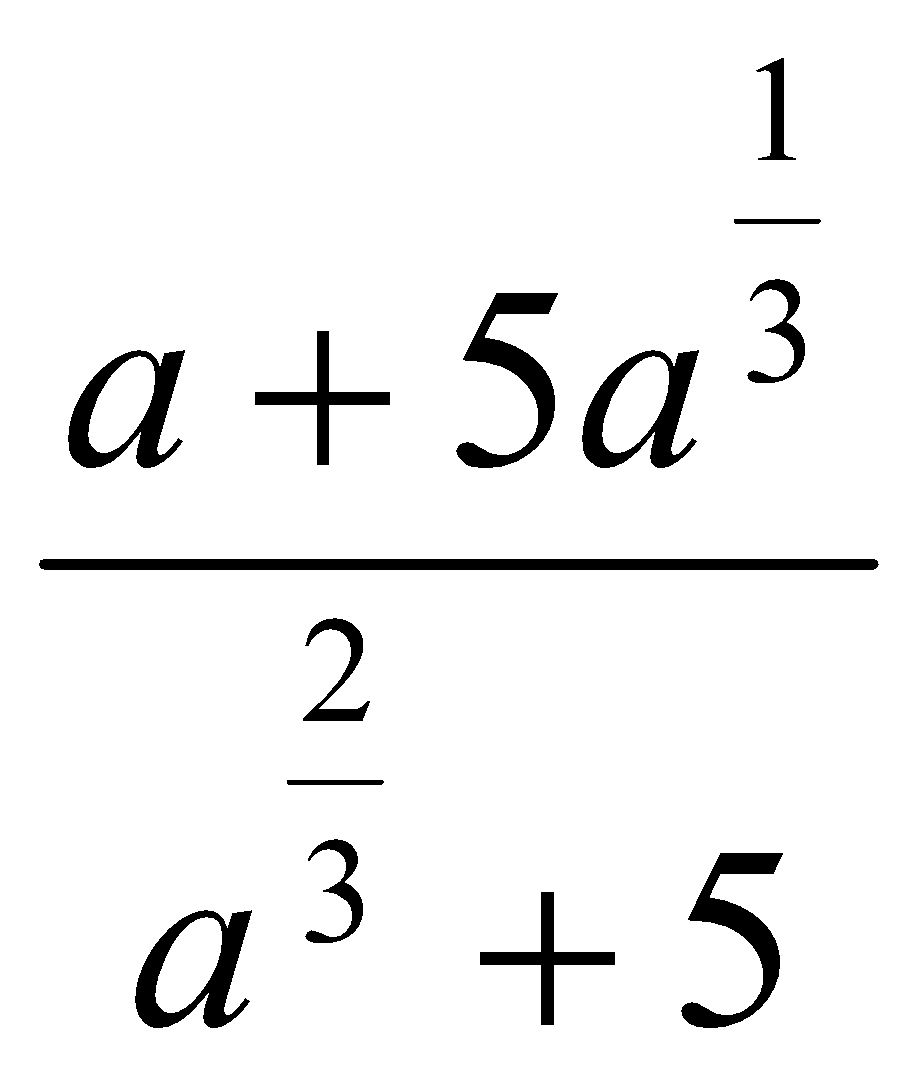 . Ответ:
. Ответ: 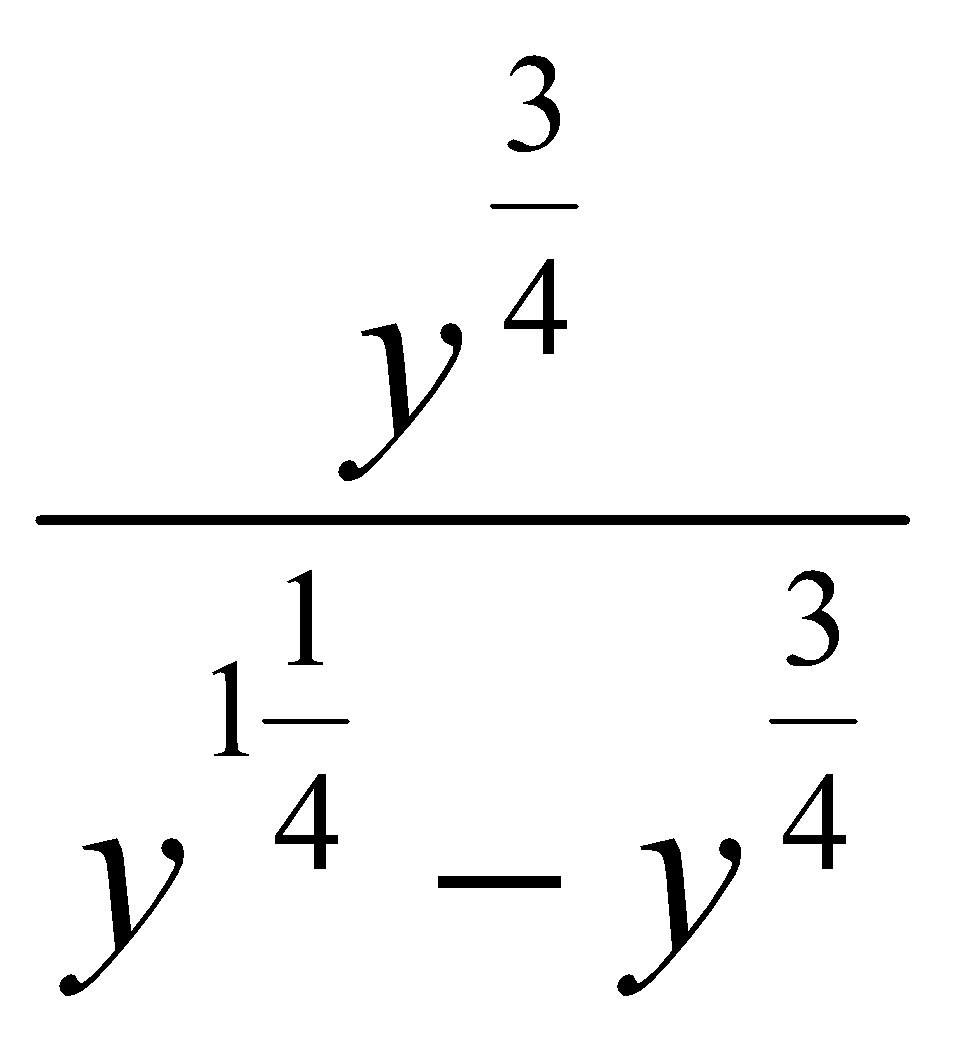 . Ответ:
. Ответ: 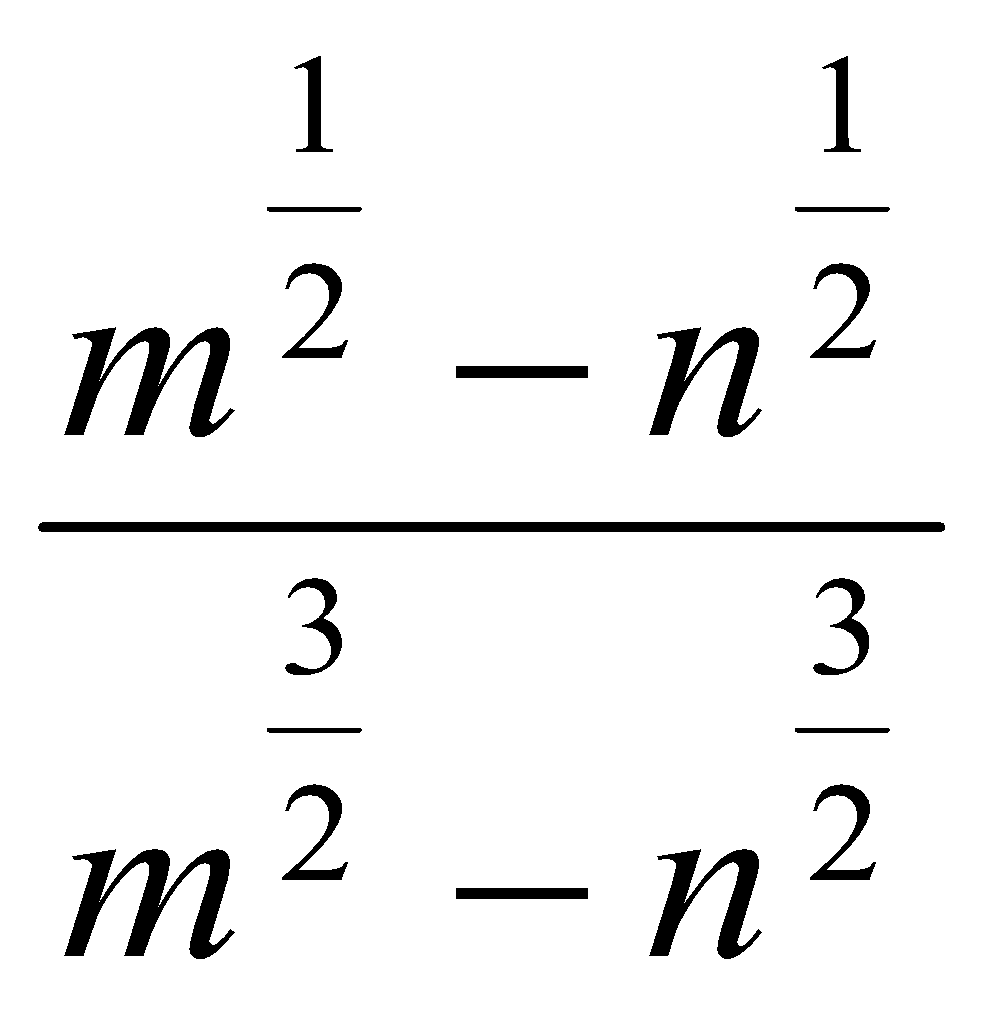 . Ответ:
. Ответ: 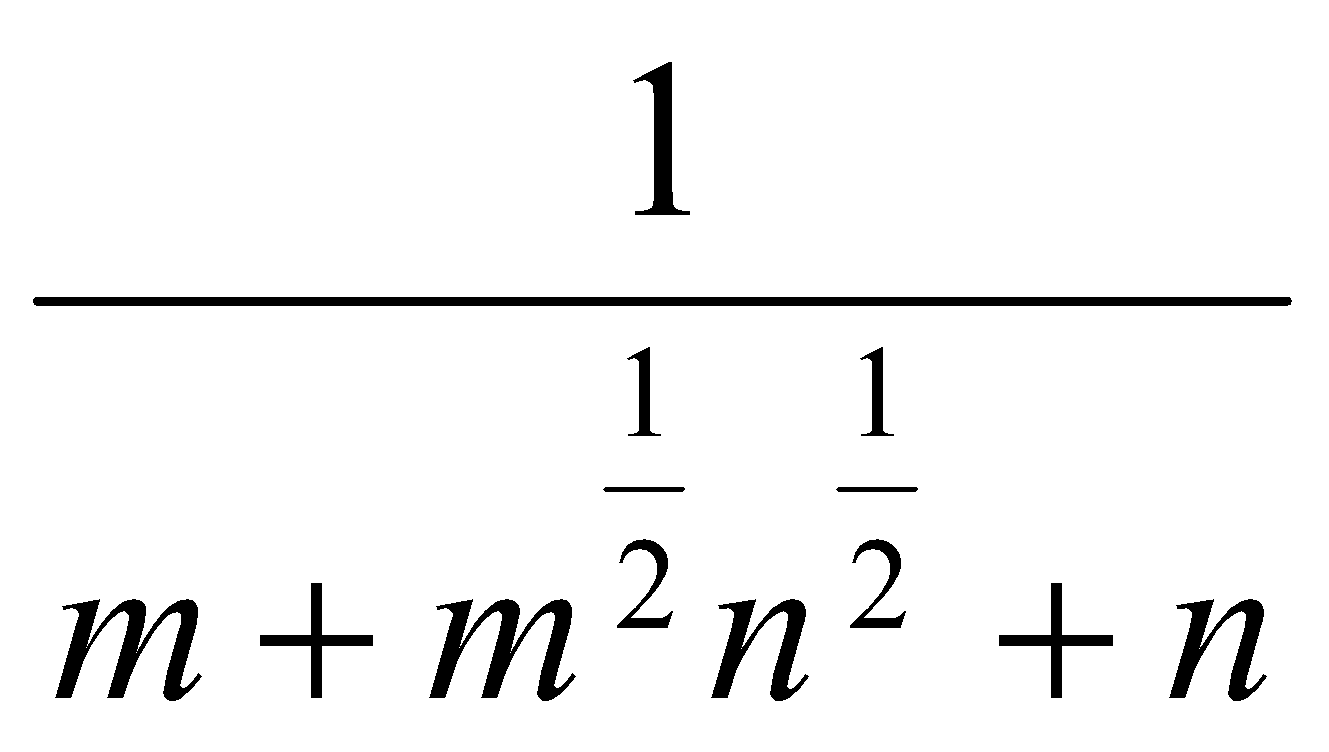 .
.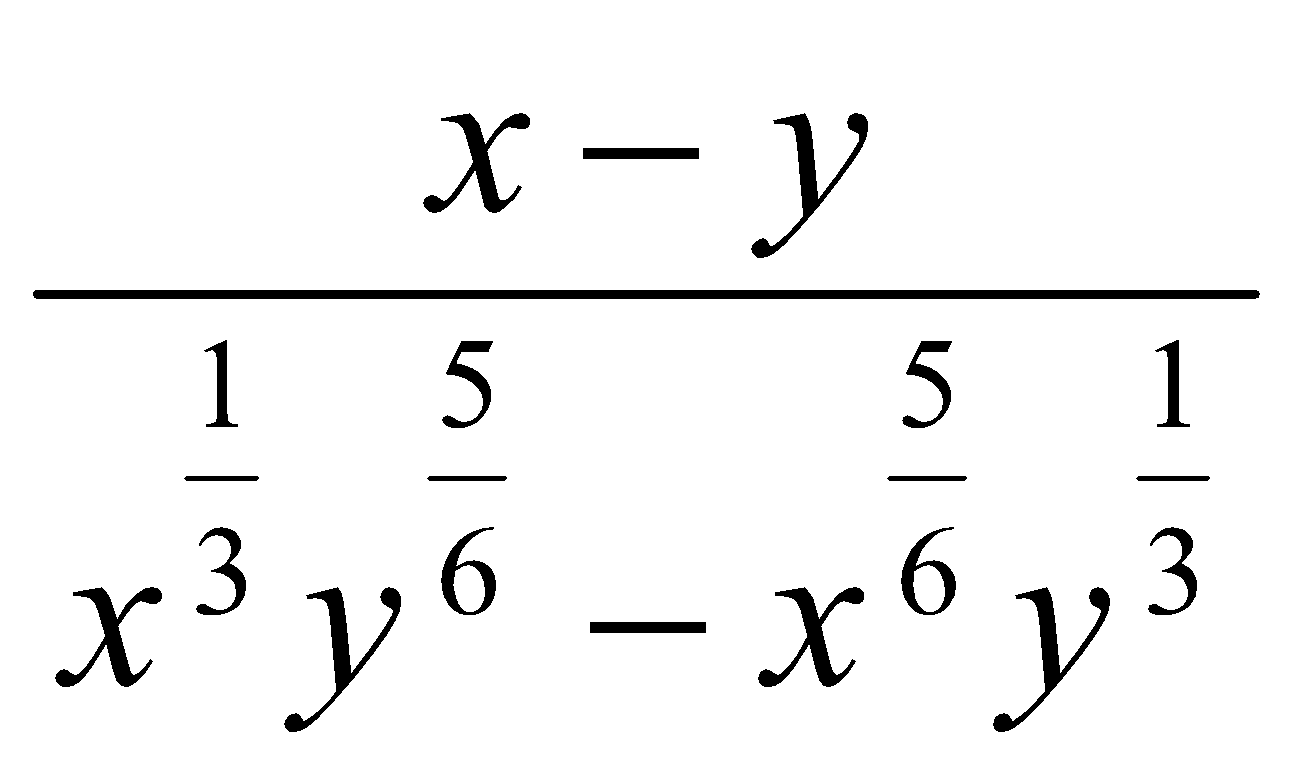 . Ответ:
. Ответ: 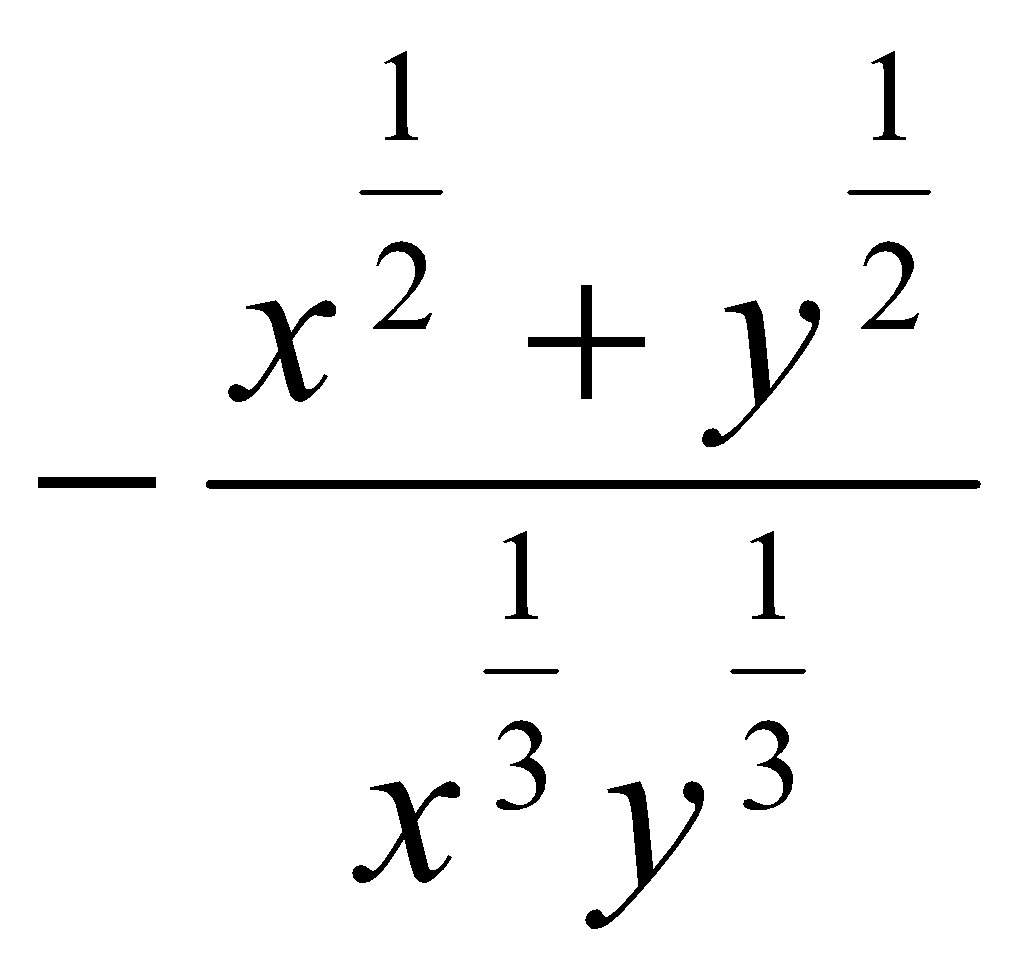 .
.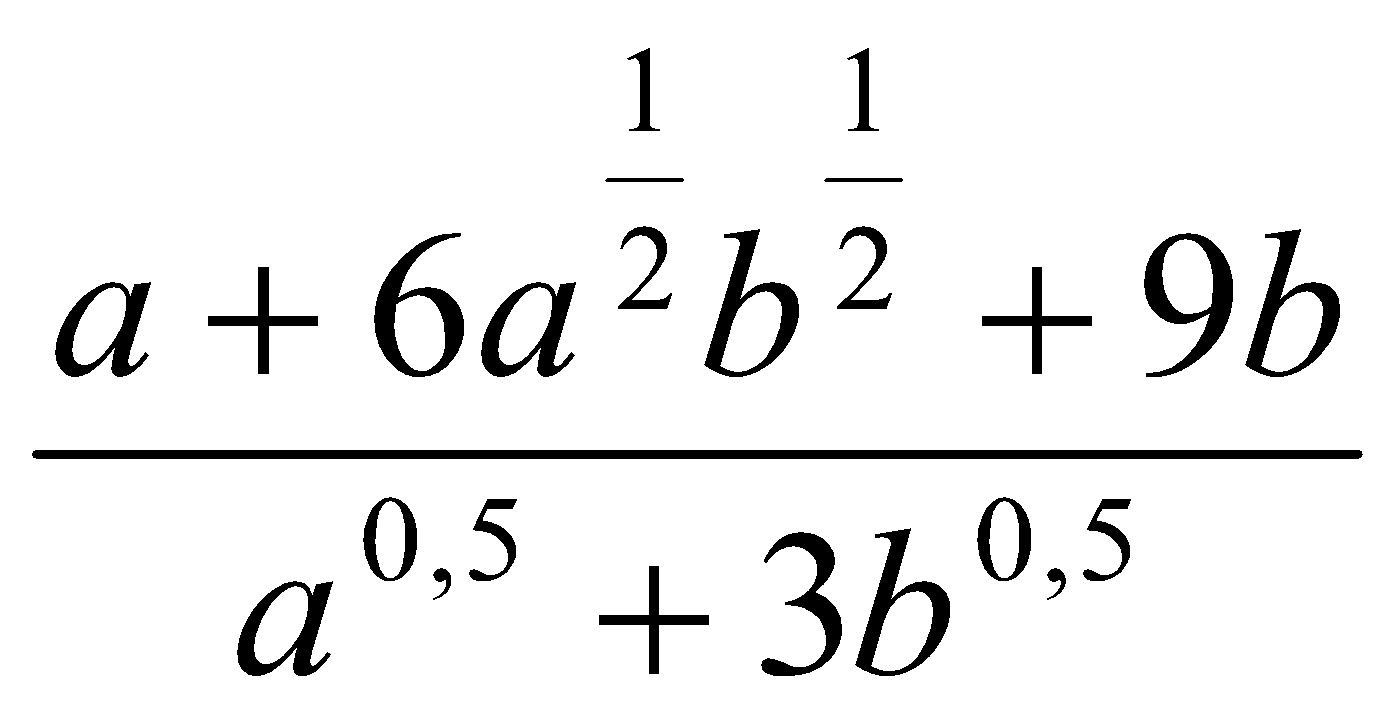 . Ответ:
. Ответ: 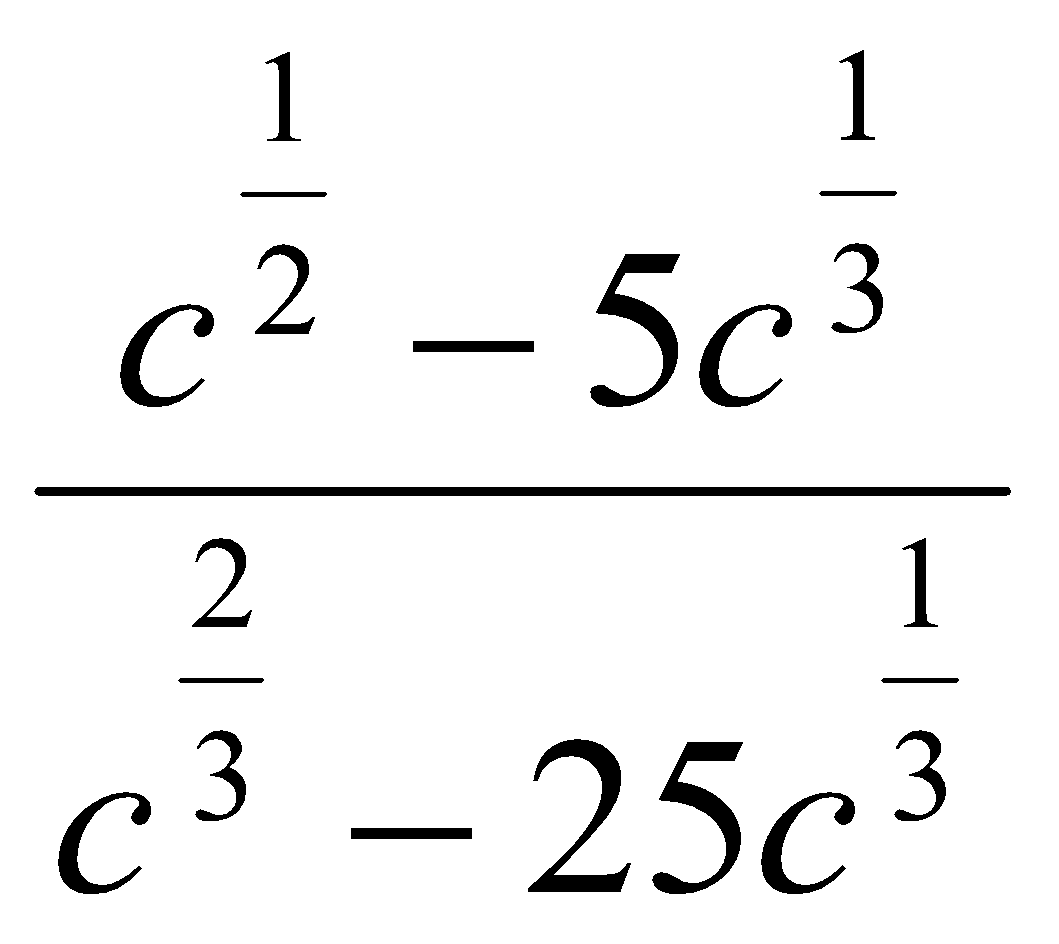 . Ответ:
. Ответ: 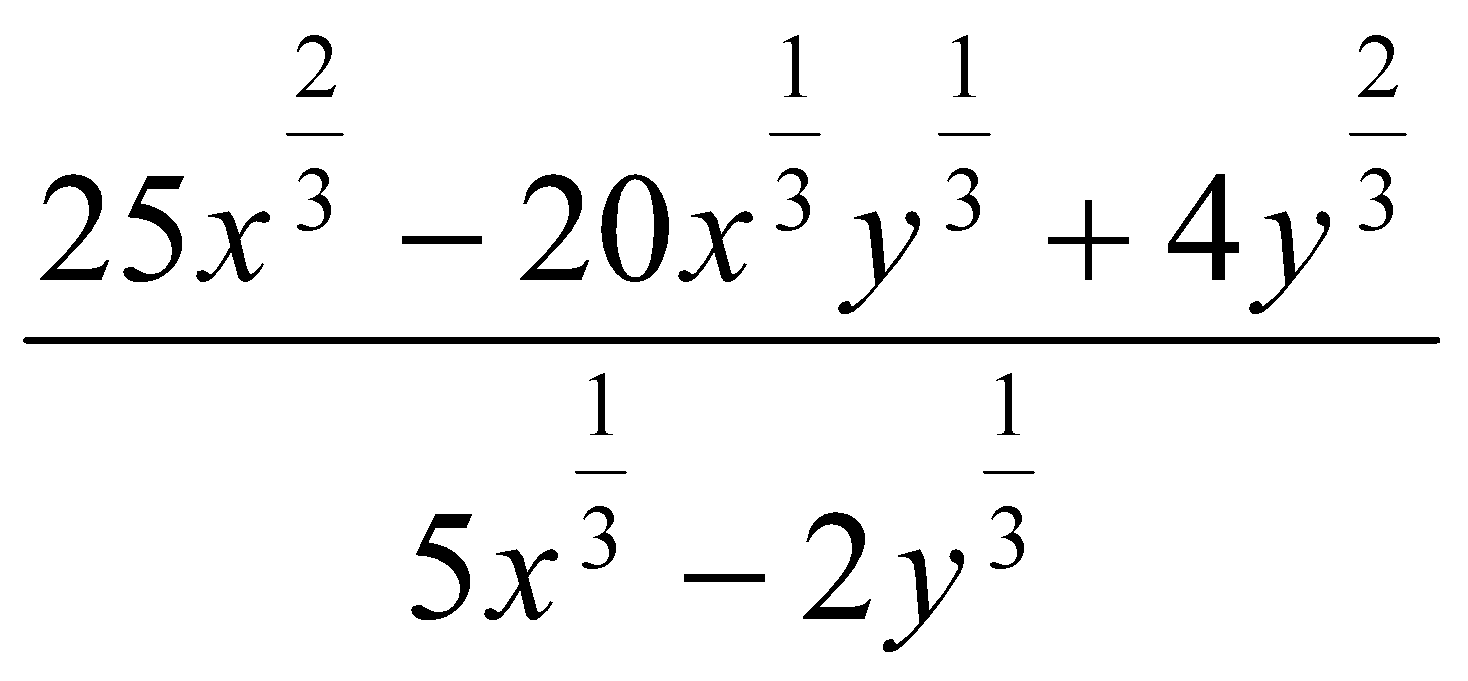 .
.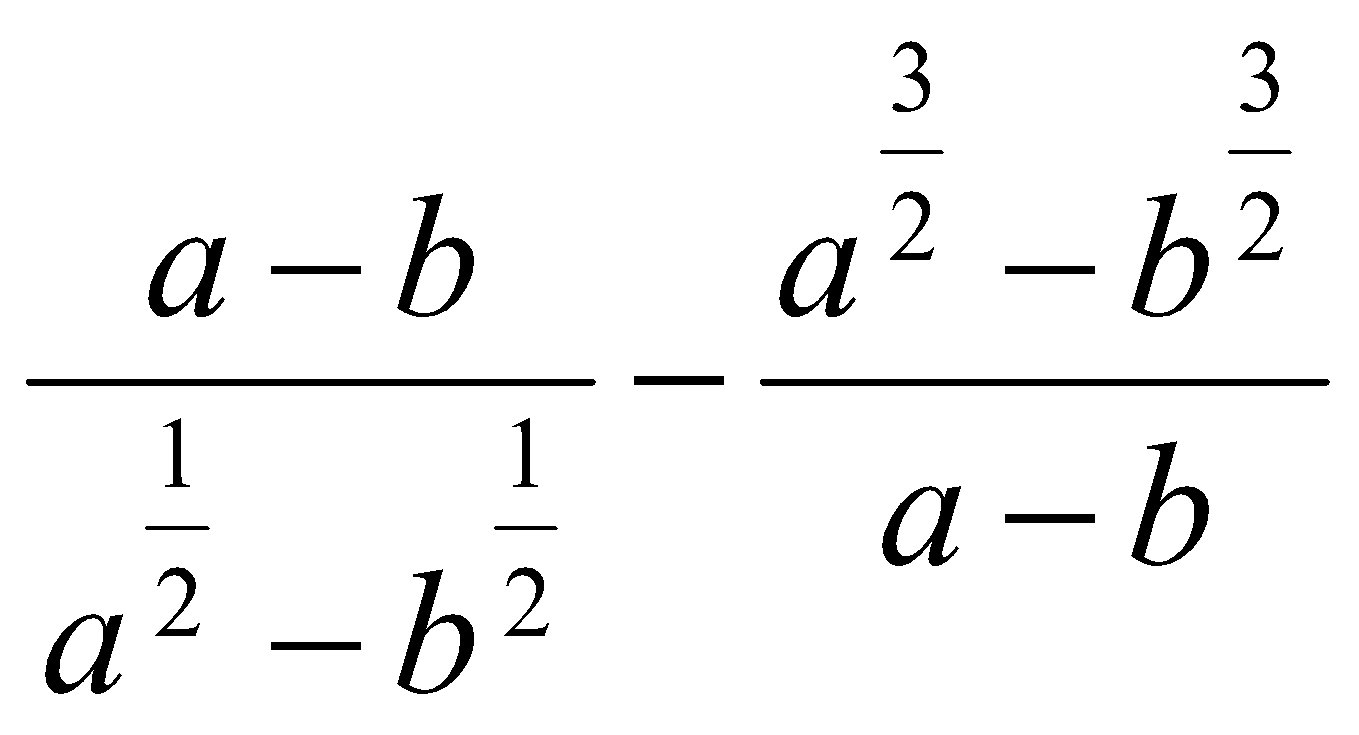 . Ответ:
. Ответ: 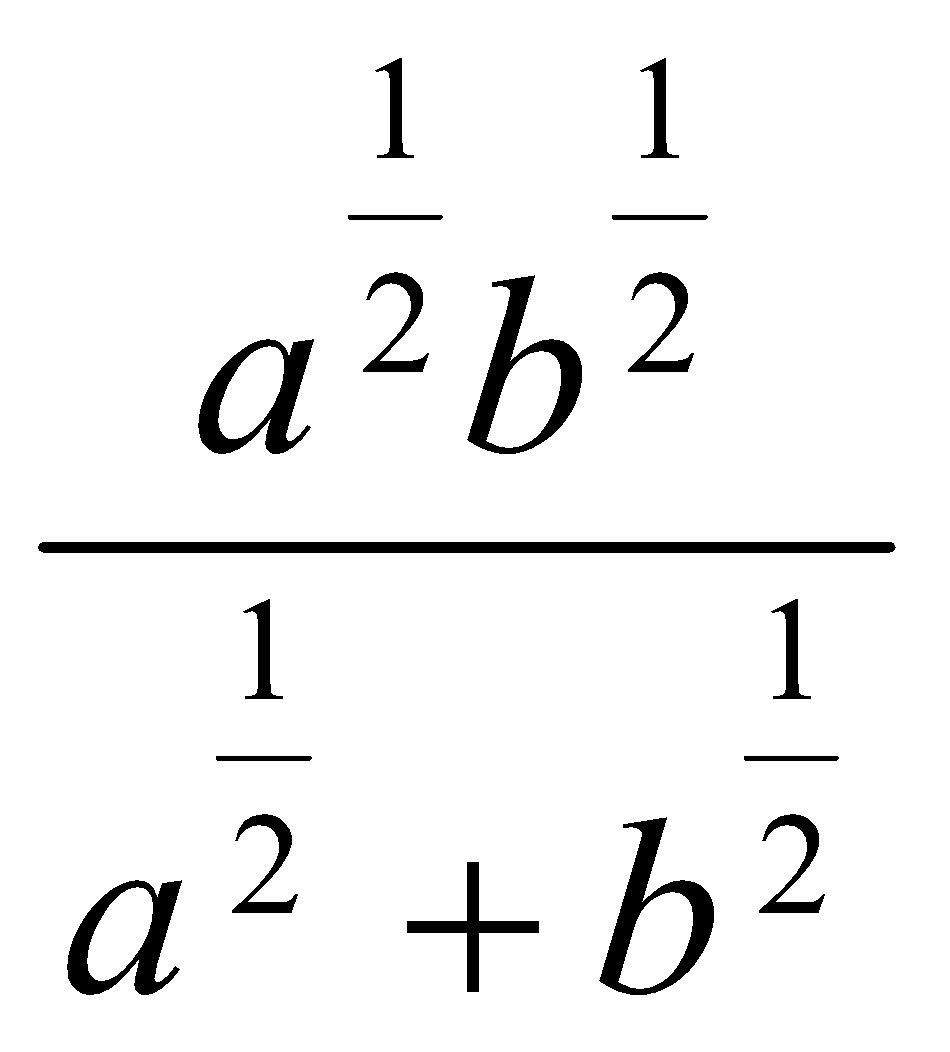 .
. . Ответ:
. Ответ: 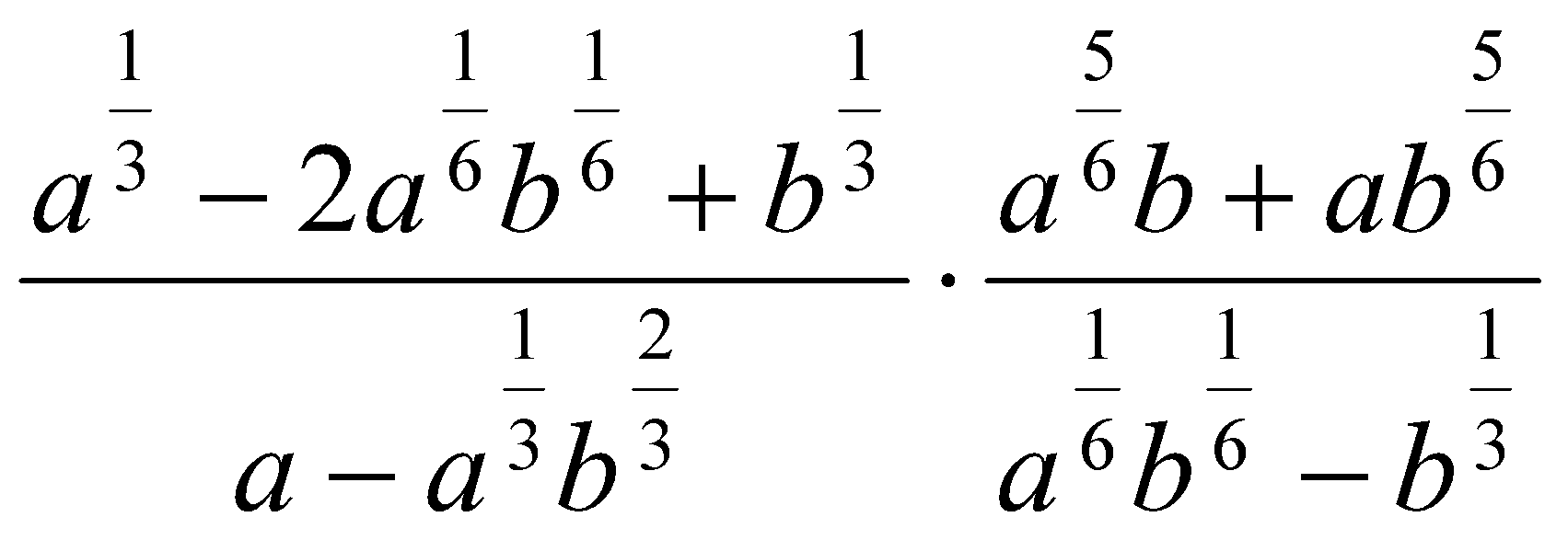 .
.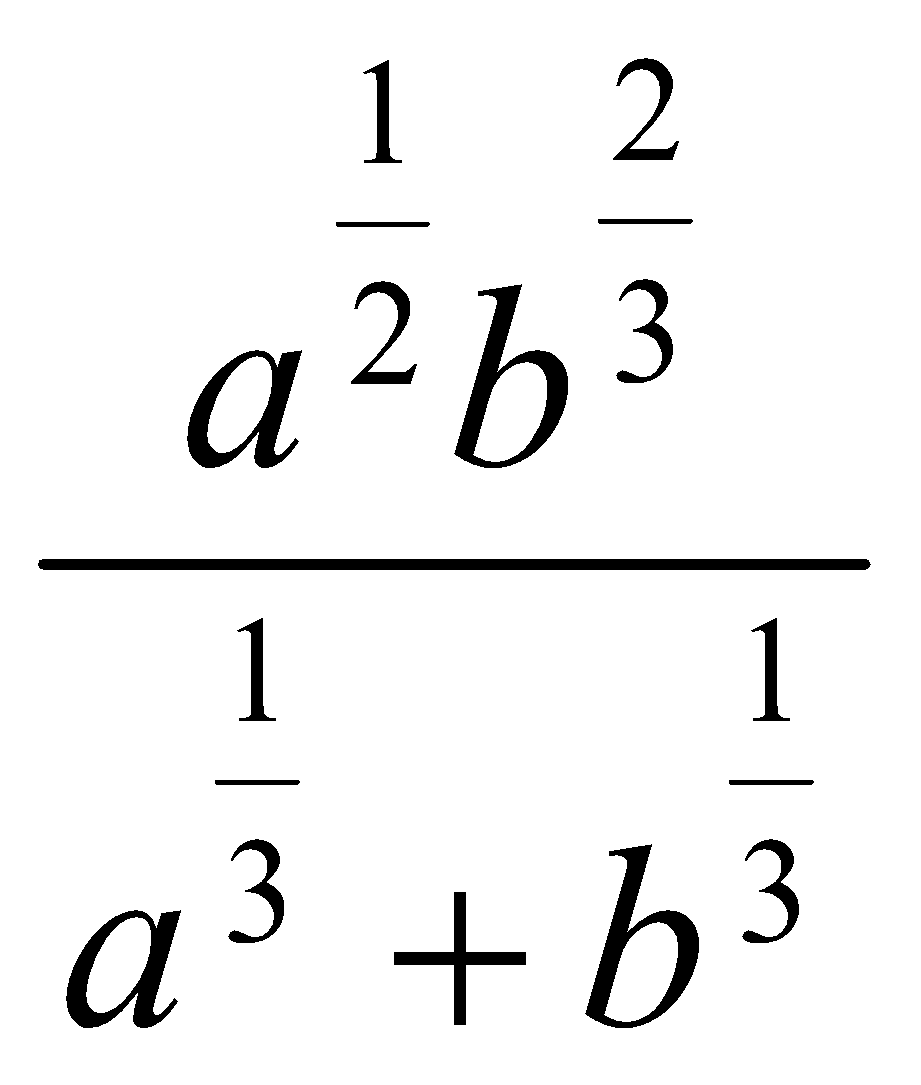 .
.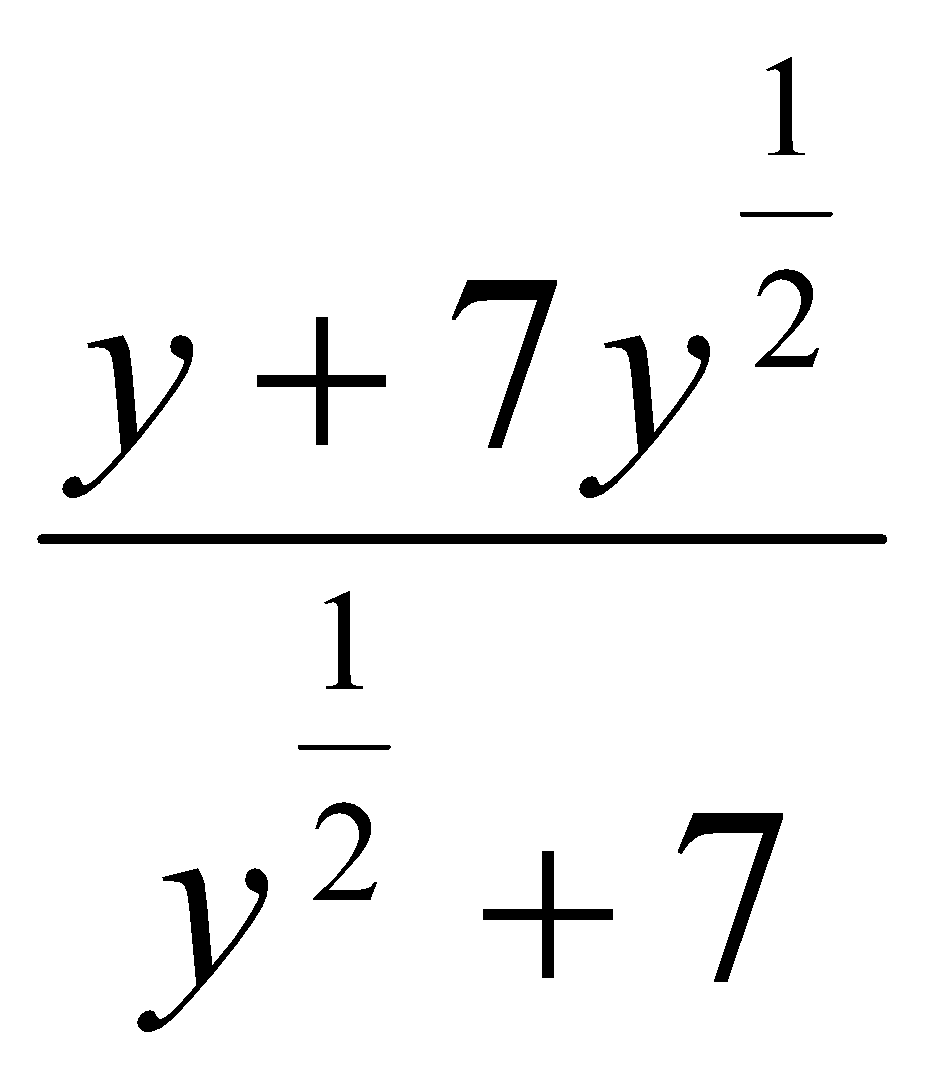 . Ответ:
. Ответ:  . Ответ:
. Ответ: 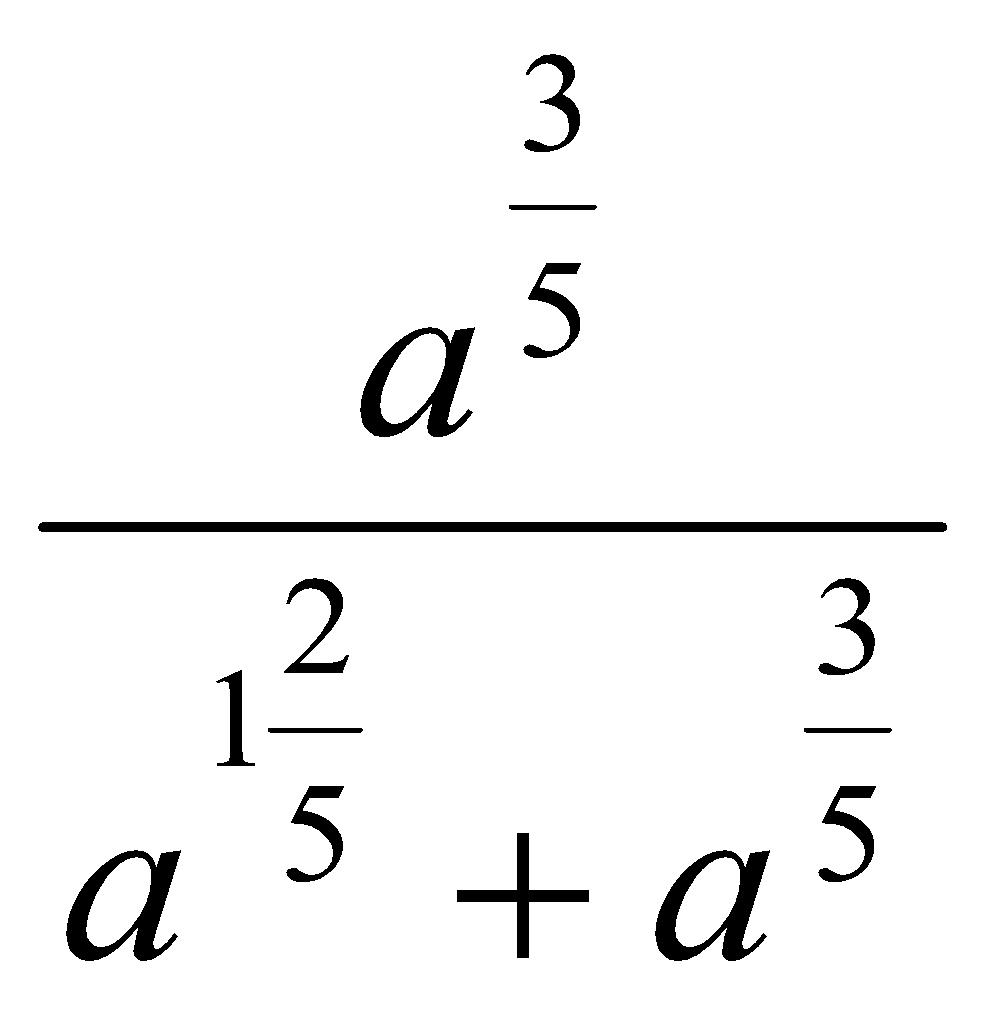 . Ответ:
. Ответ: 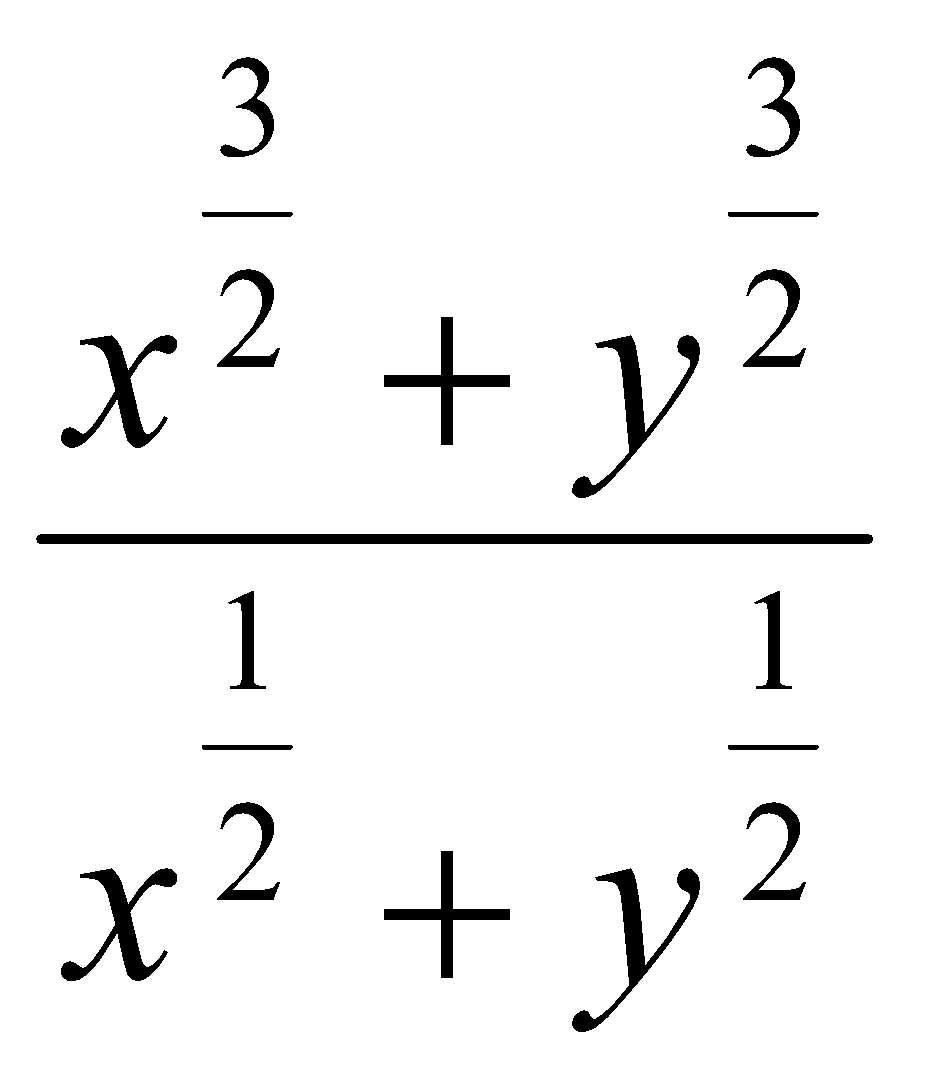 . Ответ:
. Ответ: 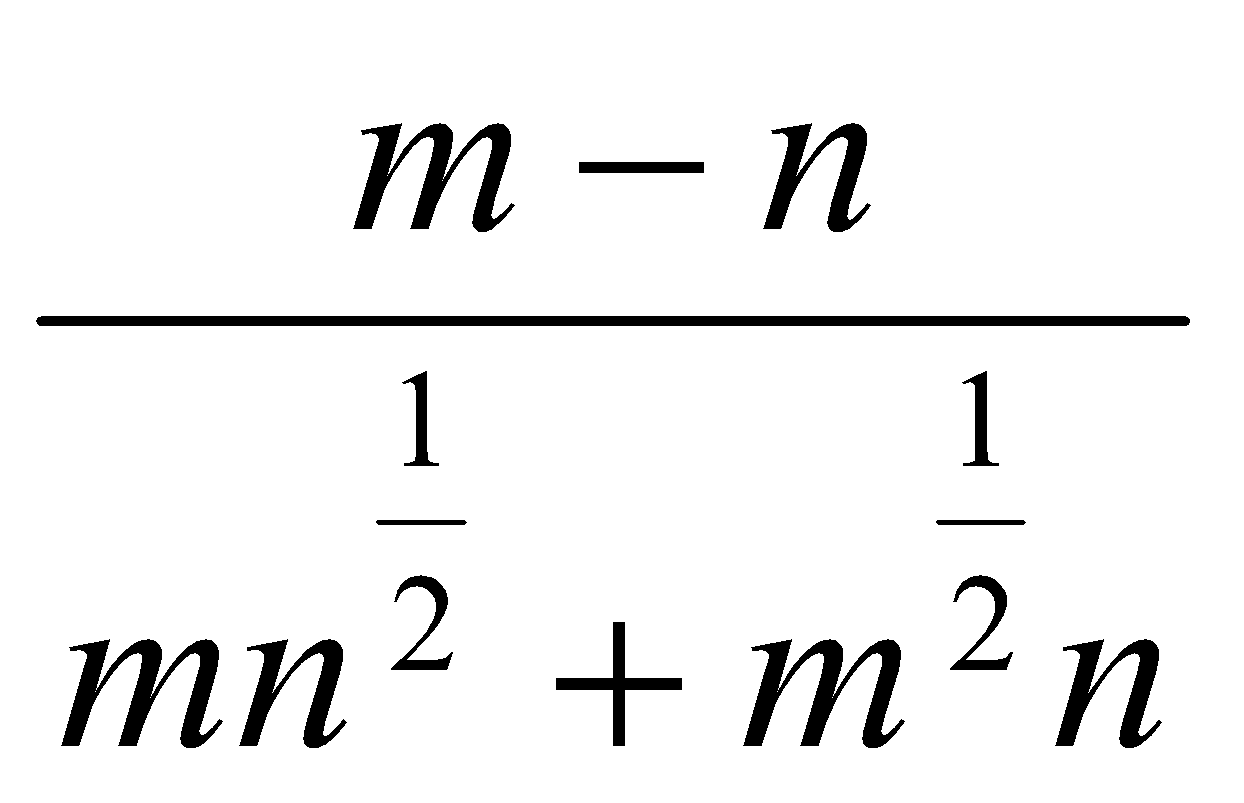 . Ответ:
. Ответ: 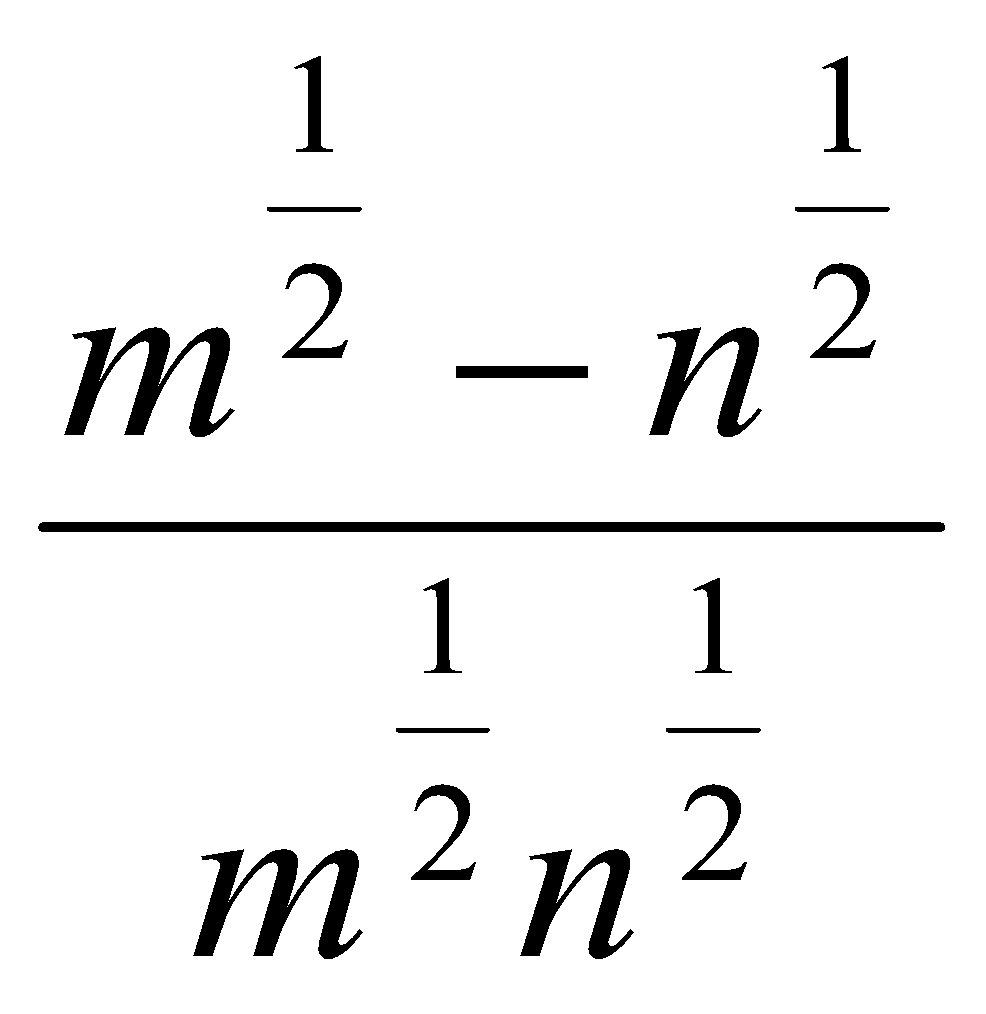 .
.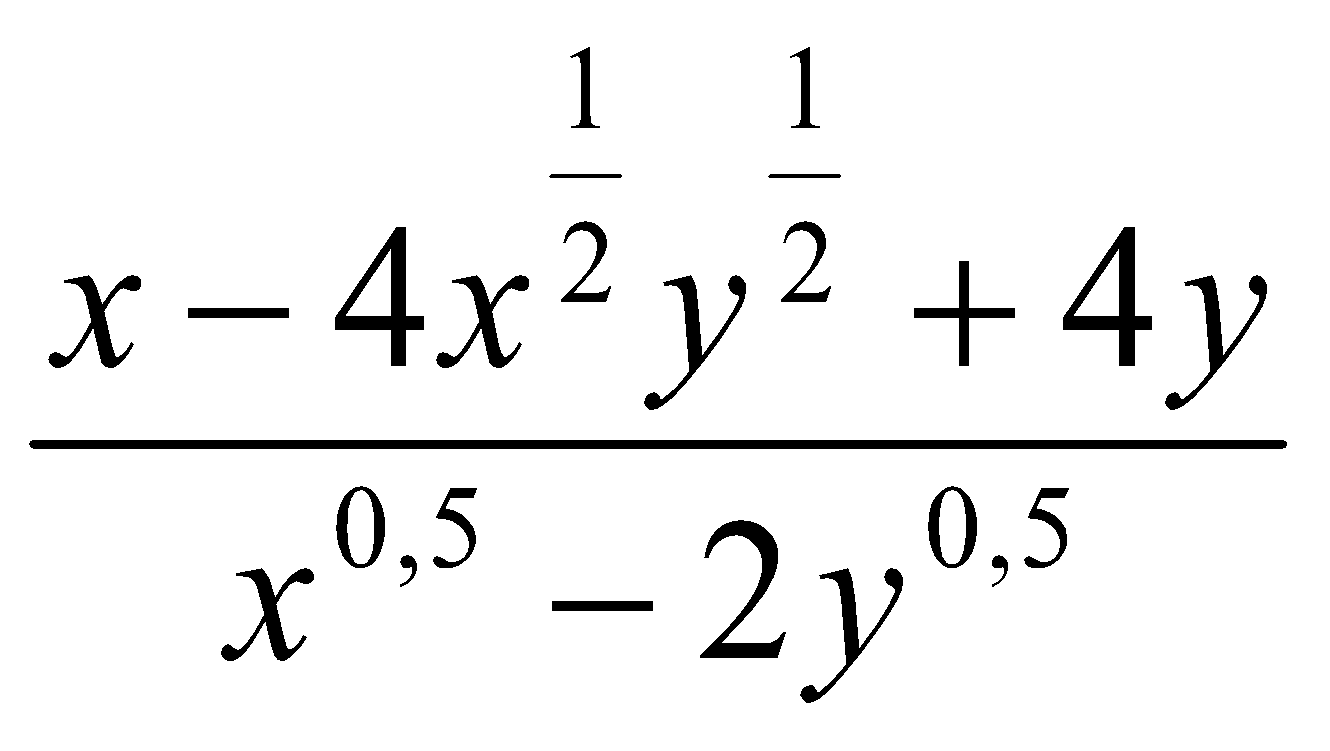 . Ответ:
. Ответ: 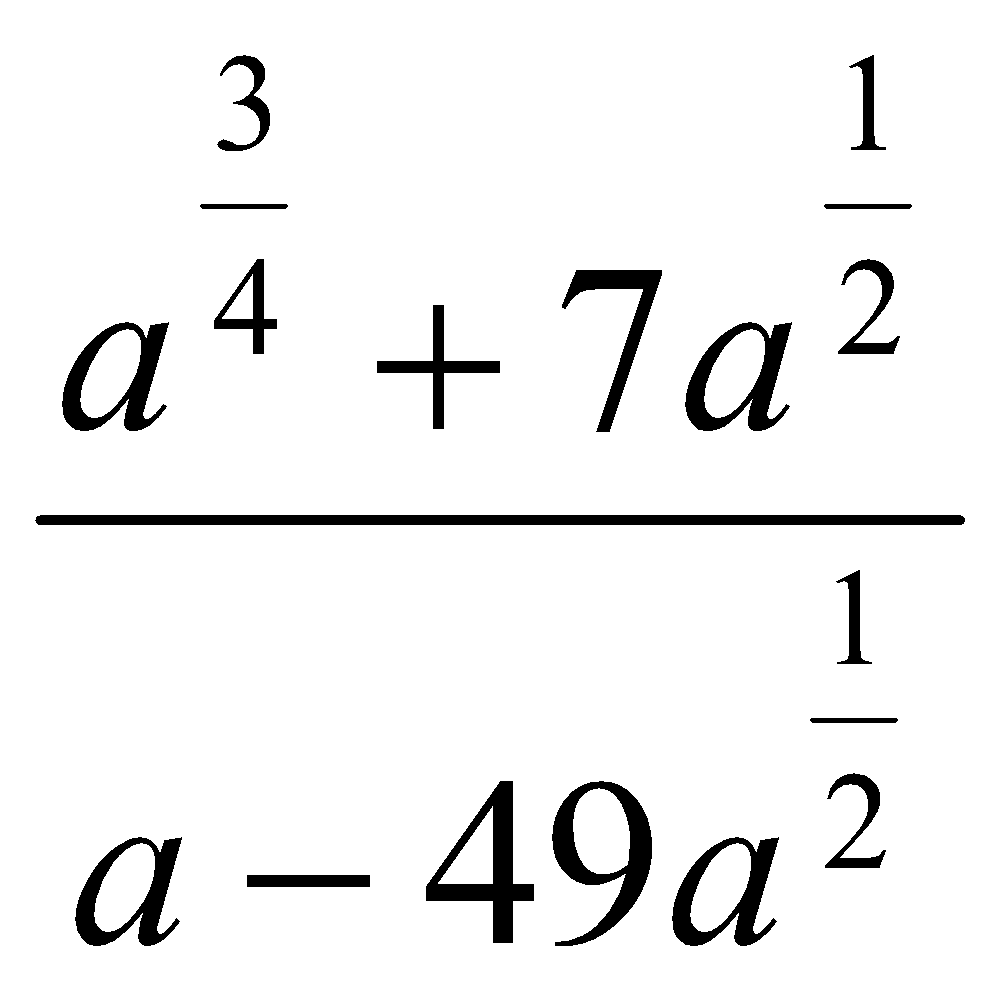 . Ответ:
. Ответ: 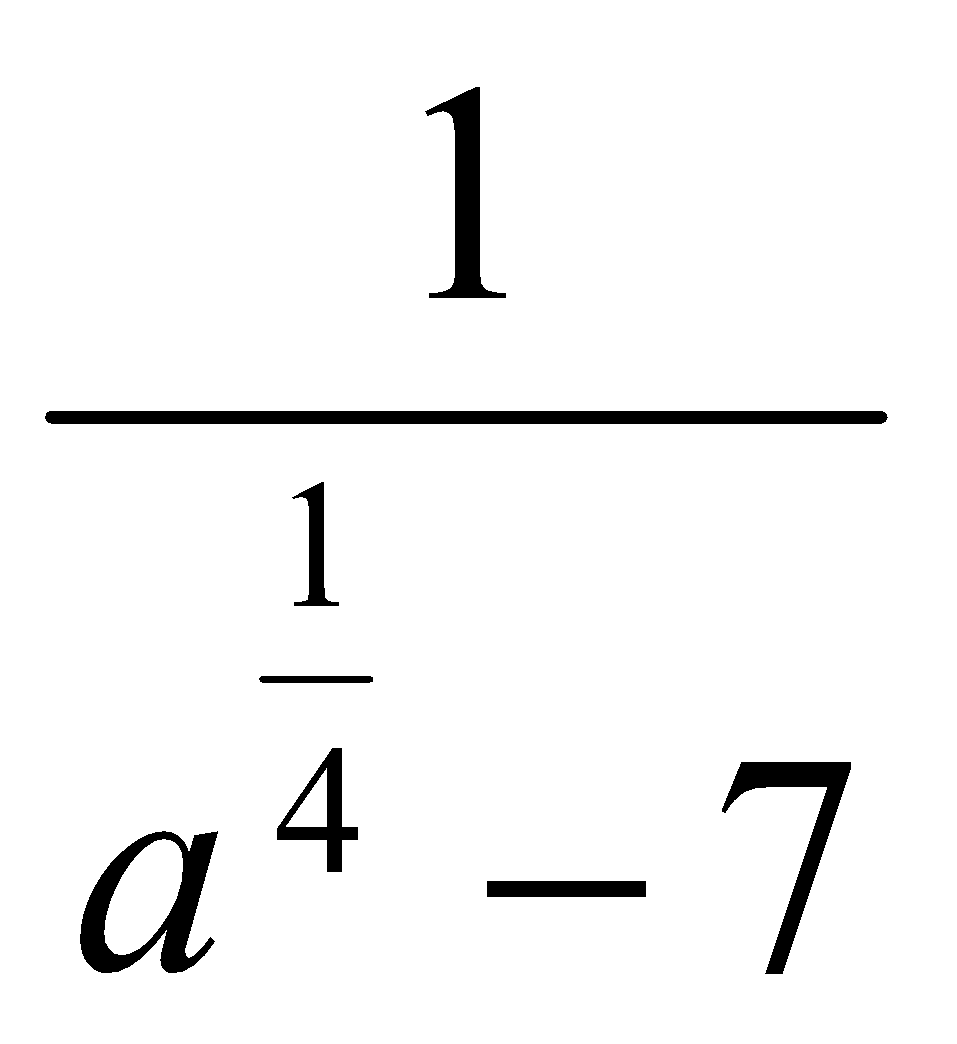 .
.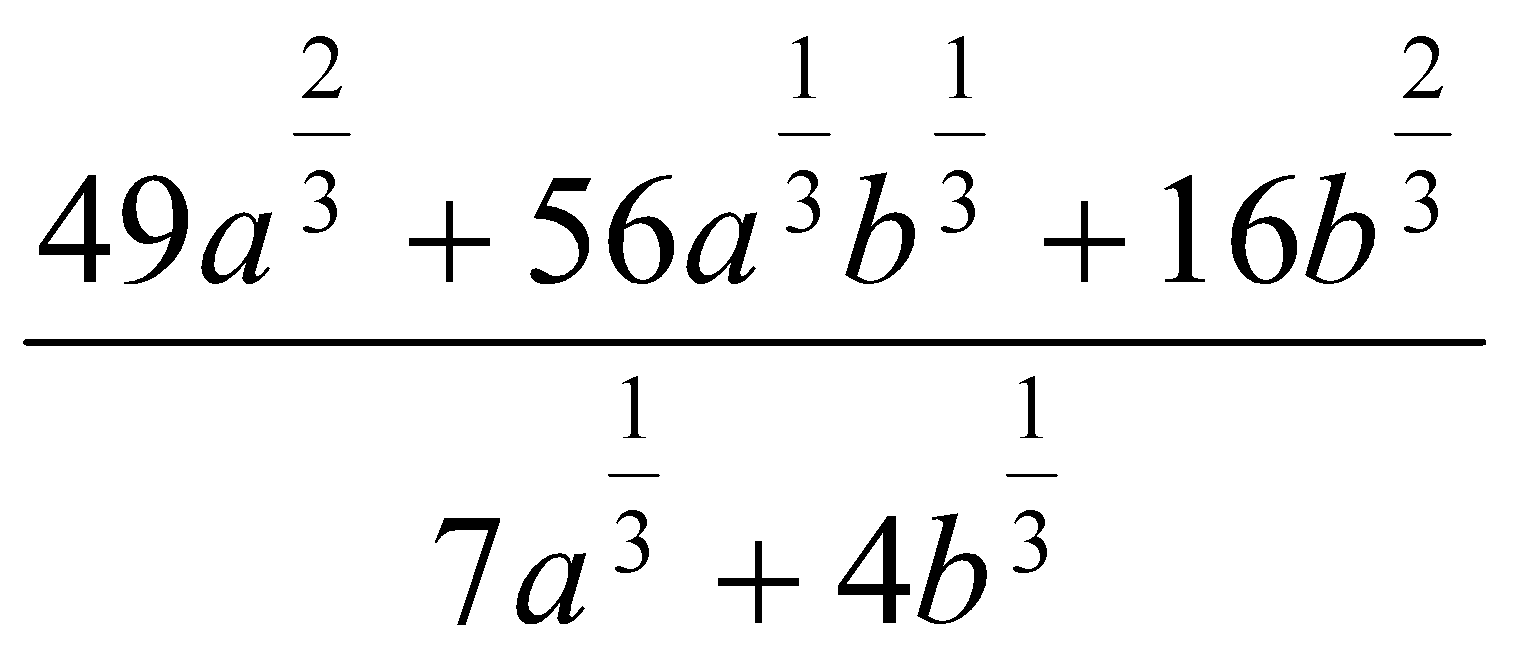 .
. 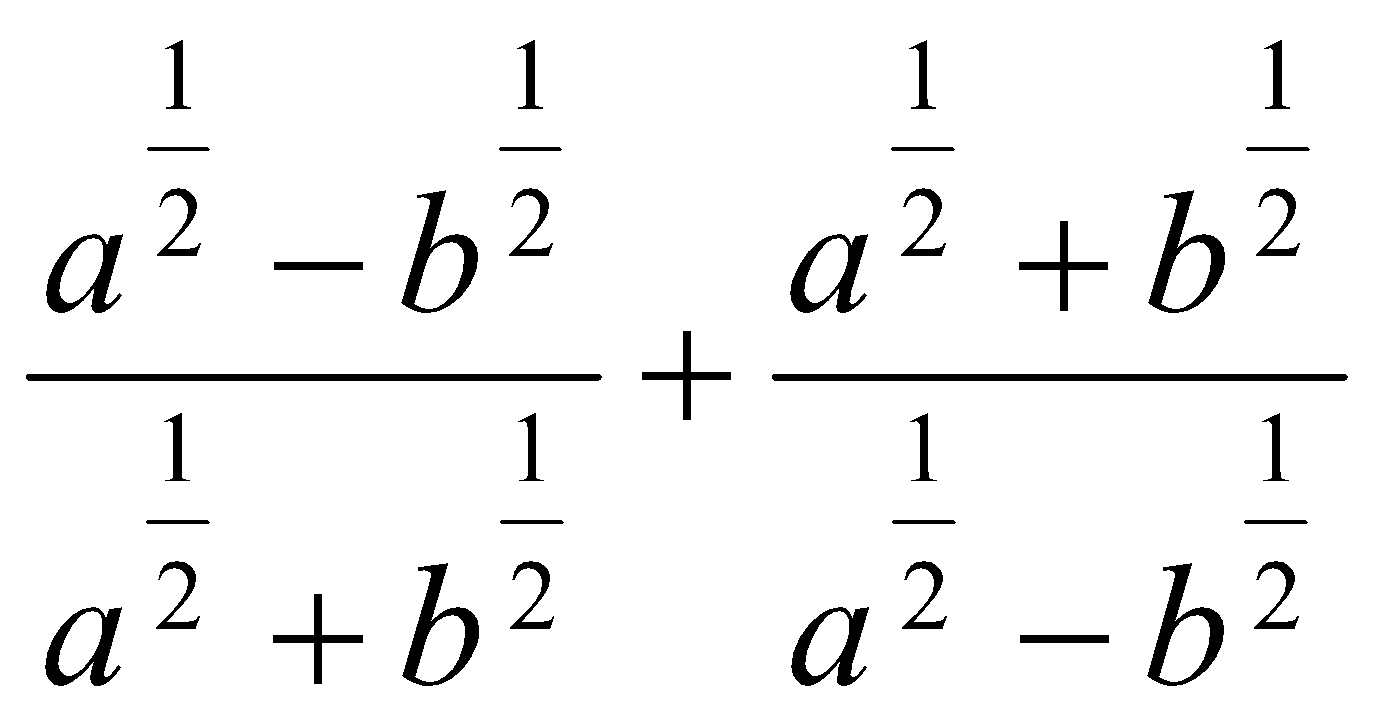 . Ответ:
. Ответ: 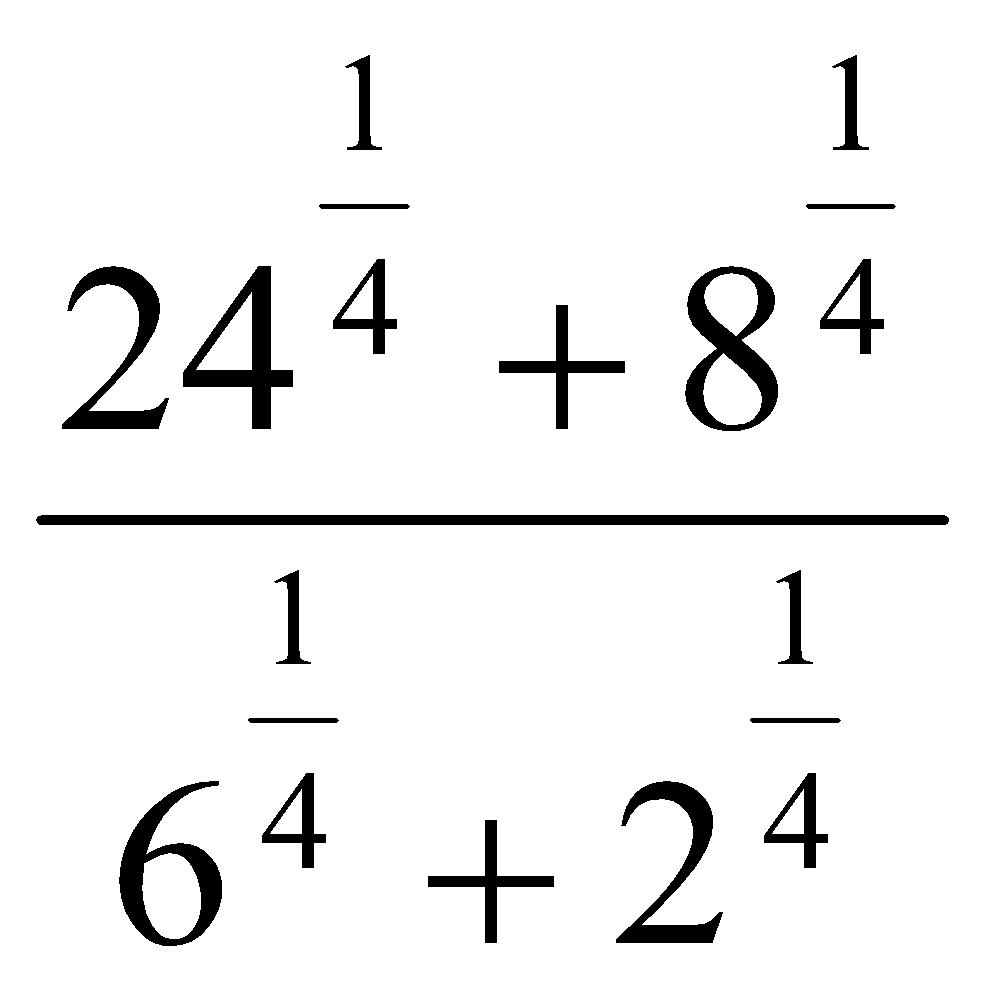 . Ответ:
. Ответ: 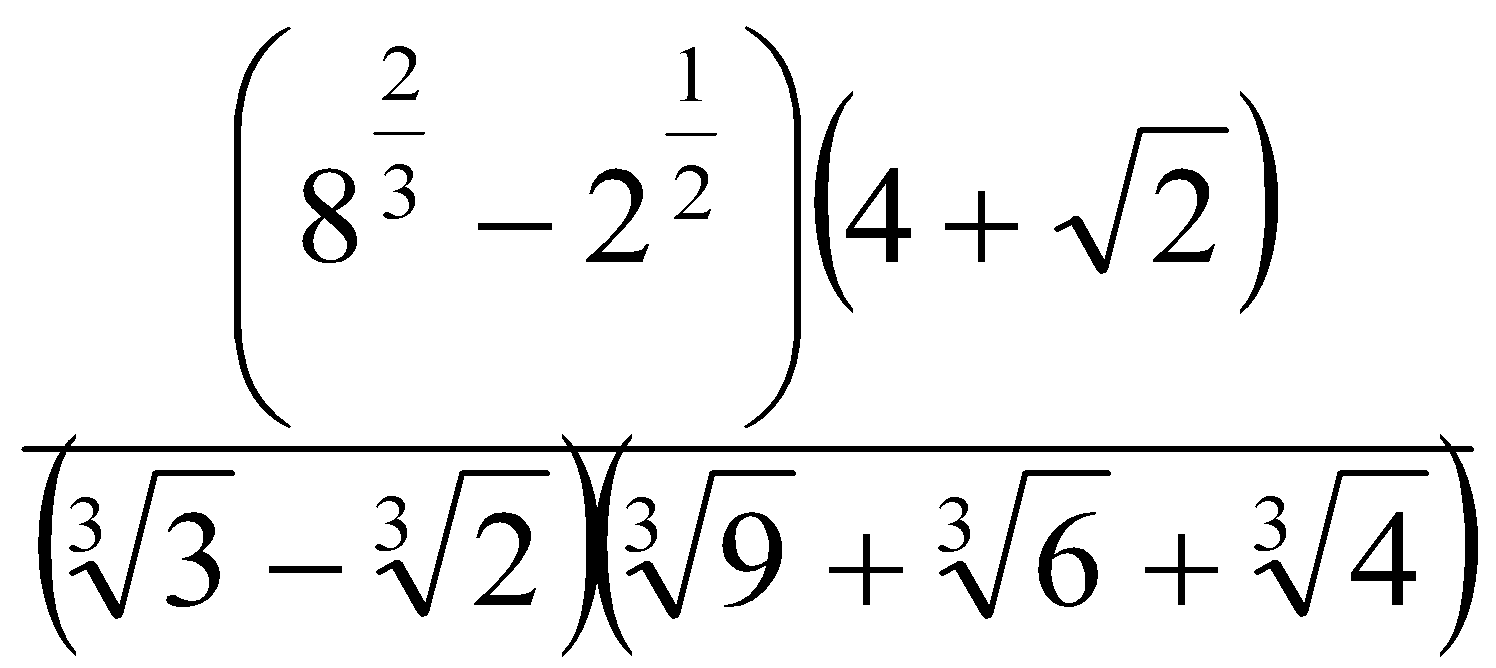 . Ответ: 14.
. Ответ: 14.