Разработка урока по геометрии "Центральная и осевая симметрия" для студентов 1 курса колледжа

Тип урока: деловая игра-конференция “Есть ли будущее без симметрии?”, интегрированный с историей , экологией, ботаникой, зоологией.

Участники урока-конференции: 3 группы учащихся 9 класса (математики, историки, естественные науки).

Цели урока:

• образовательные: изучение понятия осевой и центральной симметрий, проведение исследовательской работы по изучению явлений симметрии в природе, архитектуре и технике, приобретение навыков самостоятельной работы с большими объемами информации;

• развивающие: развитие логического мышления, творческой активности, познавательного интереса;

• воспитательные: воспитание умения сплоченно и дружно работать в коллективе, внимательно слушать речь других.

Оборудование: мультимедийная аппарат, раздаточный материал: бланки ответов, карточки с проверочной работой.

Ход урока.

1. Оргмомент.

Учащиеся разбиваются на 3 группы, учитель сообщает тему урока, тип урока, цели урока.

1. Актуализация знаний.

Вводное слово учителя.

Почему мы находим одни вещи красивыми, а другие нет? Почему некоторые люди кажутся нам более привлекательными, а другие менее? Кристи Тарлинктон, супермодель (рис.1), признанная одной из самых красивых женщин в мире, считает, что по большей части обязана своим успехом в качестве модели идеальной симметрии своих губ. Пропорция и симметрия объекта всегда необходима нашему зрительному восприятию для того, чтобы мы могли считать этот объект красивым. Баланс и пропорция частей относительно целого обязательны для симметрии. Смотреть на симметричные изображения приятней, нежели на асимметричные.

Группа математиков.

Понятие симметрии проходит через всю историю человечества. Оно встречается уже у истоков человеческого знания. Возникло оно в связи с изучением живого организма, а именно человека. И употреблялось скульпторами ещё в 5 веке до н. э.
Слово “симметрия” греческое, оно означает “соразмерность, пропорциональность, одинаковость в расположении частей”. Его широко используют все без исключения направления современной науки.

Об этой закономерности задумывались многие великие люди. Например, Л. Н. Толстой говорил: “Стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия понятна глазу? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано?”. Действительно симметричность приятна глазу. Кто не любовался симметричностью творений природы: листьями, цветами, птицами, животными; или творениями человека: зданиями, техникой, – всем тем, что нас с детства окружает, тем, что стремится к красоте и гармонии.
Герман Вейль сказал: “Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство”. Герман Вейль – это немецкий математик. Его деятельность приходится на первую половину ХХ века. Именно он сформулировал определение симметрии, установил по каким признакам усмотреть наличие или, наоборот, отсутствие симметрии в том или ином случае. Таким образом, математически строгое представление сформировалось сравнительно недавно – в начале ХХ века. Оно достаточно сложное. Мы же обратимся и еще раз вспомним те определения, которые даны нам в учебнике.

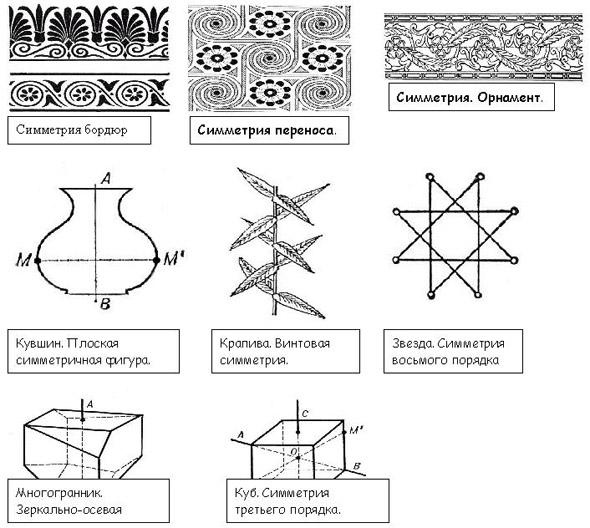
Вопросы: давайте вспомним, что такое симметрия, какие виды симметрии вы знаете? В чем особенность каждого вида симметрии?

( на слайдах определение симметрии, примеры осевой и центральной симметрии)

Задание: двое учащихся у доски выполняют построения осевой и центральной симметрий.

Дополнение учителя.

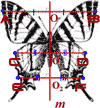
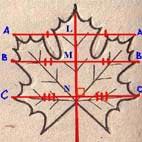
Посмотрите на кленовый лист, снежинку, бабочку (рис.2). Их объединяет то, что они симметричны. Если мысленно прочертить вертикальную прямую через центр рисунка и поставить зеркальце вдоль прочерченной на каждом рисунке прямой, то отраженная в зеркальце половинка фигуры дополнит её до целой (такой же, как исходная фигура). Поэтому такая симметрия называется зеркальной (или осевой, если речь идет о плоскости). Прямая, вдоль которой поставлено зеркало, называется осью симметрии. Если симметричную фигуру сложить пополам вдоль оси симметрии, то её части совпадут. В этом случае говорят, что дано отражение плоскости на себя.

Сравним две фигуры (кляксу и ажурную бумажную снежинку). Клякса получилась так, на лист бумаги капнули каплю чернил, сложили лист вдвое и затем разогнули. Линия сгиба – ось симметрии кляксы. Клякса имеет одну вертикальную ось симметрии. Аналогичным образом получилась снежинка, только лист бумаги согнули несколько раз, вырезали из этого “слоёного” листа кусок, а затем разогнули лист. У “снежинки” несколько линий сгиба, и все они являются осями симметрии.

У геометрических фигур может быть одна или несколько осей симметрии, а может и не быть вовсе.

Многие листья деревьев и лепестки цветов симметричны относительно среднего стебля. С симметрией мы часто встречаемся в искусстве. архитектуре. технике. быту. Так, фасады многих зданий обладают осевой симметрией. В большинстве случаев симметричны относительно оси или центра узоры на коврах, тканях, комнатных обоях (рис.3).

Задание: Группам построить фигуры, симметричные, используя осевую и центральную симметрии.

Каждой группе дано по 1 геометрической фигуре, требуется построить фигуру, симметричную данной, используя оба вида симметрии.

Группа экспертов естественных наук.

Прежде чем познакомить Вас с результатами нашего исследования, мы представим вам науку Ботанику.
Ботаника – наука о растениях. Она охватывает огромный круг проблем: их систематику; развитие в течение геологического времени; возможности хозяйственного использования растений; закономерности внешнего и внутреннего строения растений.
Наше исследование было направлено на выявление примеров симметрии в растениях, то есть мы занимались последней из этих проблем – проблемой поиска закономерностей внешнего строения растений.
Этот вопрос возник ещё в 5 веке до н. э. На явление симметрии в живой природе обратили внимание в Древней Греции пифагорейцы в связи с развитием ими учения о гармонии. В 19 веке появлялись отдельные работы, касающиеся этой темы. А в 1961 году как результат многовековых исследований, посвященных поиску красоты и гармонии окружающей нас природы, появилась наука биосимметрика.
Для представления итогов нашей работы мы выбрали некоторые растения.

Начнем с показа примеров осевой симметрии в ботанике.

Ребята представляют рисунки с различными частями растений, обладающими осевой симметрией ,.

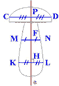
Дальнейшие наши поиски были сосредоточены на центральной симметрии. Она наиболее характерна для цветов и плодов растений. Центральная симметрия характерна для различных плодов, но мы остановились на ягодах: голубика, черника, вишня, клюква. Рассмотрим разрез любой из этих ягод. В разрезе она представляет собой окружность, а окружность, как нам известно, имеет центр симметрии.
Центральную симметрию можно наблюдать на изображении следующих цветов: цветок одуванчика, цветок мать-и-мачехи, цветок кувшинки, сердцевина ромашки, а в некоторых случаях центральной симметрией обладает и изображение всего цветка ромашки. На данном рисунке представлена ромашка . Её сердцевина представляет собой окружность, и поэтому центрально симметрична, так как мы знаем, что окружность имеет центр симметрии. Весь же цветок обладает центральной симметрией только в случае четного количества лепестков. В случае же нечетного количества лепестков, вспомните анютины глазки , он обладает только осевой.

Выводы:

1. По нашим наблюдениям, в любом растении можно найти какую-то его часть, обладающую осевой или центральной симметрией. Это могут быть листья, цветы, стебли, стволы деревьев, плоды, и более мелкие части, такие как сердцевина цветка, пестик, тычинки и другие.

2. Осевая симметрия присуща различным видам растений и грибам, и их частям.

3. Центральная симметрия наиболее характерна для плодов растений и некоторых цветов.

Дополнение учителя.

Рассмотрим, как связаны животный мир и симметрия. Сначала расскажем, что же такое зоология и чем эта наука занимается. Её предмет – изучение животного мира и именно строения и деятельности тела животных, их развития, распределения по земле и отношений к окружающей (животной и мертвой) природе. Конечная цель ее – выяснение законов, управляющих явлениями животного мира, объяснение с их помощью происхождение современного мира животных и установление естественной системы животных.

Существует множество таких законов и один из них это закон симметрии. Как мы знаем, на плоскости существует два вида симметрии: осевая и центральная. Наше исследование заключалось в поиске примеров этих двух видов симметрии в животном мире.

Начнём с осевой симметрии. По нашим наблюдениям, она присуща большому количеству видов животных. Мы остановили свой выбор на тех животных, которые занесены в “Красную книгу”, чтобы ещё раз подчеркнуть необходимость заботливого отношения к братьям нашим меньшим. Ребята представляют животных различных видов, для некоторых из них проводят математическое обоснование
, , .

Теперь рассмотрим центральную симметрию. По нашим наблюдениям, центральная симметрия наиболее характерна для животных, ведущих подводный образ жизни , .

Мы также нашли пример асимметричных животных: инфузория-туфелька и амёба .

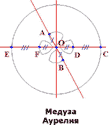
Симметрия у живых организмов служит не только для красоты; она прежде всего связана с приспособлением их к окружающему миру, с их жизнестойкостью. Организмам на протяжении эволюции приходилось приспосабливаться к проявлению действия законов природы (поворотная симметрия – медузы, морские звезды).

Зеркальной симметрией обычно обладают листья растений – удивительно симметричны листья дуба, вербы, клена, крапивы. Многие цветы, в частности колокольчик, нарцисс, анютины глазки, обладают характерным свойством: цветок можно повернуть на некоторый угол так, что каждый лепесток займет положение соседнего; иными словами, цветок совместится сам с собой. Такой цветок обладает поворотной осью симметрии. Наиболее ходовые цветы, те у которых между лепесточками 72°. Подобные оси – пример элементов симметрии, то есть геометрических образов, используемых для описания формы симметричных тел. Заметим, что необходимый для совмещения угол поворота в разных случаях неодинаков. Для цветка колокольчика он равен 72°, для нарцисса – 60°. Минимальный угол, на который нужно повернуть цветок вокруг оси симметрии, чтобы он совместился с сами собой, называется элементарным углом поворота оси.

Задание: Каким видом симметрии обладает каждое из предложенных изображений цветов, плодов, растений, животных?

Учащимся предлагаются рисунки, под которыми следует сделать запись. Дополнительно необходимо указать, если рисунок имеет несколько осей симметрии.

Группа историков и архитекторов.

Красота и гармония тесно связаны с симметрией, это подметили еще древние архитекторы и художники. Слово симметрия происходит от греческого “sum metria”, что означает "такая же мера". Греческий скульптор Поликлеитос очевидно был первым, кто использовал этот термин еще в XV веке до н.э.. Во времена Пифагора ( 5 в. до нашей эры) и пифагорейцев понятие симметрии было оформлено достаточно четко. Огромное внимание уделялось правильным пропорциям человеческого тела.

Архитектура – удивительная область человеческой деятельности. В ней тесно переплетены и строго уравновешены наука, техника, искусство. Только соразмерное, гармоничное сочетание этих начал делает возводимое человеком сооружение памятником архитектуры. Архитектурный облик здания архитектор создает с помощью строительного материала, образ же его созидается творческим мышлением. Одним из художественных средств, которые он использует, является композиция здания. От неё в первую очередь зависит впечатление, которое оставляет архитектурное сооружение. Мы предлагаем Вам прогуляться по Петербургу и особенно обратить внимание на композиции зданий нашего города, на их симметричность.
Начнем с XVIII века. Именно в это время началась застройка нашего города. Из зданий этого века мы представим Вам здание Кунсткамеры, сооруженного в 1718-1734 годах на Васильевском острове.
К середине XVIII века архитектурный облик Петербурга становится все более торжественным и нарядным. Эта эпоха оставила замечательные образцы стиля барокко. Этот стиль отличается присутствием криволинейных форм. Грандиозные архитектурные ансамбли (группа зданий, объединенных общим замыслом) поражают воображение множеством украшений на фасадах. Архитектурные формы изгибаются, переплетаются со скульптурой. Примером является Екатерининский дворец, воздвигнутый по проекту Ф.-Б. Растрелли в Царском селе. В этом же стиле воздвигнуты по проектам С. И. Чевакинского Никольский морской собор и дворец Шереметьевых. Проведём математическое обоснование осевой симметрии фасада Никольского морского собора .

Во второй половине XVIII - первой трети XIX века Петербург приобрёл воспетый А.С. Пушкиным “строгий, стройный вид”, который придала городу архитектура классицизма. Все здания, построенные в стиле классицизм, имеют четкие прямолинейные симметричные композиции. На фоне гладких стен выступают портики и колоннады, которые придают сооружениям торжественную монументальность и парадность. Проведём математическое обоснование осевой симметрии фасада Таврического дворца .

В начале XIX века по проекту А.Н. Воронихина было сооружено выдающееся произведение искусства – Казанский собор. Перед Казанским собором симметрично установлены памятники М.И. Кутузову и М.Б. Барклаю-де-Толли, полководцам, разгромившим армию Наполеона.

Выводы:

1. Принципы симметрии являются основополагающими для любого архитектора, но вопрос о соотношении между симметрией и асимметрией каждый архитектор решает по-разному. Асимметричное в целом сооружение может являть собой гармоническую композицию симметричных элементов.

2. Удачное решение определяется талантом зодчего, его художественным вкусом и его пониманием прекрасного. Прогуляйтесь по нашему городу и убедитесь, что удачных решений может быть очень много, но неизменным остается одно – стремление архитектора к гармонии, а это в той или иной степени связано с симметрией.

Задание: Назовите как можно больше примеров симметрии в нашем городе.

После фронтального опроса учащихся на экране появляются некоторые примеры симметрии в городе Лабытнанги.

VII. Заключительное слово учителя.

Вопросы: 1) Какие виды симметрии вы знаете?

2) Приведите примеры из окружающего нас мира с осевой симметрией, с центральной симметрией.

Итак, наша конференция подошла к концу. Попробуем подвести итоги. Вы прослушали сообщения исследовательской работы всех групп. Мы прокатились в машине времени и увидели, что симметрия присутствует и в прошлом и в будущем. Симметрия – это не только математическое понятие. Его заимствовали из природы. А так как человек – это часть природы, то человеческое творчество во всех его проявлениях тяготеет к симметрии. Симметрия в живой природе: в животном и растительном мире, – передается генетически из поколения в поколение.

И на вопрос: “Есть ли будущее без симметрии?” мы можем ответить словами классика современного естествознания, мыслителя Владимира Ивановича Вернадского “Принцип симметрии охватывает все новые и новые области…”

Каждый из Вас получит отметку, которая будет складываться из всех составляющих: ваша активность при подготовке к конференции, результаты выполненных заданий и ответы на уроке.
Наша конференция завершается. Вы узнали много нового и, несомненно, по-другому будете смотреть на окружающий нас мир.

VIII. Домашнее задание: приведите примеры явлений осевой и центральной симметрии из тех областей, которые мы не рассмотрели во время конференции. Найдите информацию о «Золотом сечении» и числах Фибоначчи, имеющих к нашей теме непосредственное отношение.

Дополнительно: №1148.