Глава 3 Операции над событиями, сложение вероятностей (3 ч.)
Урок 1. Тема урока: Операции над событиями: пересечение, объединение событий. Диаграммы Эйлера.
Основные задачи урока: Рассмотреть три основных события: пресечение, объединение, переход к противоположному событию. Рассмотреть изображение диаграмм Эйлера, показать их применение при решении задач
Примерный план проведения урока:
-
В начале урока можно отметить, что операции над событиями учащимся известны еще из курса информатики. Три основные операции над случайными событиями, которые рассматриваются в курсе «Вероятность и статистика» это пересечение, объединение и переход к противоположному событию. По сути это операции над множествами элементарных событий. Для демонстрации материала можно использовать слайды (см ссылку в приложении к уроку).
-
Для обозначения множества всех элементарных событий случайного эксперимента будем использовать символ Ω (читается –– «омега»). Событие Ω является объединением всех элементарных событий опыта, поэтому оно является достоверным событием. С другой точки зрения можно считать, что событие Ω –– это и есть весь случайный эксперимент. Мы будем рассматривать дискретные случайные эксперименты.
-
Операции с двумя или тремя событиями удобно изображать с помощью диаграмм Эйлера. Диаграмма Эйлера со случайными событиями A и B показана на рис. 1
-
| 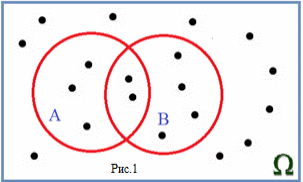
| Прямоугольник изображает множество Ω, круги –– события A и B. Точки символически изображают элементарные события эксперимента. |
-
Записать определение пересечения события. Проиллюстрировать кругами Эйлера.
Определение:
| Пересечением событий A и B называется событие, элементарные исходы которого принадлежат и событию A, и событию B. Пересечение событий A и B обозначается A∩B. Это выражение читается «пересечение A и B» или просто «A и B» |
| 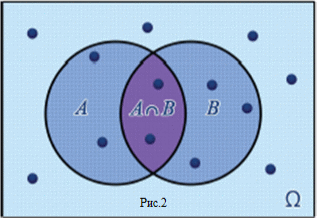
| Пересечение событий –– это их общая часть. На диаграмме Эйлера показаны два события A и B и их пересечение. Событию принадлежат те элементарные исходы, которые принадлежат обоим событиям.
|
-
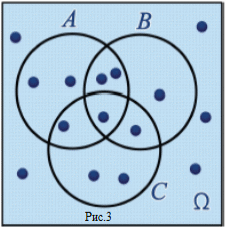
Задание: Определить по рисунку (Рис 3), сколько элементарных событий благоприятствует событиям
| 
|
A∩B (3 события) A∩С (2 события) С∩B (2 события) A∩B∩С (1 событие)
|
-
Записать определение несовместных событий. Проиллюстрировать кругами Эйлера.
Определение:
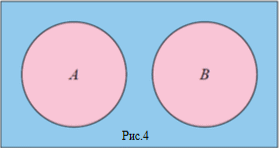
| Если события A и B не имеют общих элементарных исходов, то такие события называются непересекающимися или несовместными |
|
|
Пересечение несовместных событий не содержит элементарных событий. Его обозначают символом Ø и называют пустым событием. Это событие невозможное; P(Ø)=0. |
-
Записать определение объединения события. Проиллюстрировать кругами Эйлера.
Определение:
| Объединением событий A и B называется событие, элементарные исходы которого принадлежат хотя бы одному из событий A и B. Объединение событий A и B обозначается AU B. Это выражение читается «объединение A или B» или просто «A или B». |
| 
| На диаграмме Эйлера показаны два события A и B и их объединение. Событию принадлежат те элементарные исходы, которые принадлежат хотя бы одному из событий |
-
В тетради учащиеся могут сделать таблицу из записанных определений
| Название операции | Запись | Чтение | Изображение |
| Пересечение событий А*В произведение | A∩B | A и B | 
|
| Объединение событий А+В сумма | AUB | A или B | 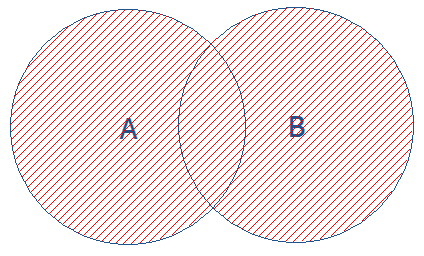
|
-
Для классной и домашней работы можно использовать следующие задачи.
Пример 1. Классный руководитель выбирает наугад двух учеников 10 класса в качестве ведущих для конкурса (сначала одного ученика, а потом другого).
Пусть событие А состоит в том, что первый ведущий — юноша, а событие В - в том, что второй ведущий тоже юноша. В чём тогда состоит событие A∩B?
Ответ: оба ведущих — юноши.
Пример 2. Бросают игральный кубик. Рассмотрим события А «выпадет больше двух очков» и В «выпадет чётное число очков»:
А = {3, 4,5, 6}и B{2,4,6}.
Два элементарных исхода благоприятствуют обоим из этих событий: {4}
и {6}. Эти элементарные события образуют новое событие — пересечение событий A∩B:
A∩B= {4,6}
Пример 3. Игральный кубик бросают дважды. Событие А заключается в том, что при втором броске выпало более трёх очков, событие В заключается в том, что при первом броске выпало менее трёх очков. Отметьте в таблице эксперимента элементарные исходы, соответствующие пересечению этих событий.
Желательный результат обсуждения.
| 
| В таблице эксперимента событие А выделим желтым цветом, а событие В отметим крестиками. Элементарные исходы, отмеченные и цветом, и крестиками, образуют событие .A∩B Чтобы непосредственно найти вероятность пересечения событий A и B, нужно учесть вероятности только тех элементарных исходов, которые принадлежат одновременно обоим событиям |
В приведённом примере событие A∩B состоит из шести элементарных исходов. Общее число элементарных исходов в опыте 36. Следовательно, .
Р (A∩B)=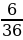 =
= 0,167
0,167
Пример 4. Термометр измеряет температуру в комнате. Пусть событие А состоит в том, что температура окажется не ниже 18°С, а событие В - в том, что температура окажется не выше 22°С. Опишите событие A∩B
Желательный результат обсуждения. В случае, когда множество элементарных событий непрерывно, удобно отметить события А и В и их пересечение на числовой прямой

Событие A∩B состоит в том, что температура окажется в пределах от 18°С до 22°С.
Остальные разработки можно посмотреть по ссылке https://vk.com/urokimatemati4ki
Пример 8. Игральный кубик бросают дважды. Рассмотрим события А «сумма выпавших очков делится на 2» и В «сумма выпавших очков делится на 3».
Какие элементарные исходы благоприятствуют объединению этих событий? Сколько их?
Желательный результат обсуждения. Отметим в таблице все элементарные исходы, благоприятствующие этим событиям. Если отмечать эти исходы в одной таблице, то мы получим событие, являющееся объединением событий А и В: AUB = «сумма выпавших очков делится на 2 или на 3».

Событию А благоприятствует 18 элементарных исходов, событию В , а событию AUB — 24 (это значение меньше суммы 18+12). Обсуждение должно привести к тому, что здесь имеются исходы, благоприятствующие обоим событиям одновременно (когда сумма очков делится на 6).
Пример 9. Термометр измеряет температуру в комнате. Событие А состоит в том, что температура окажется ниже 18°С, а событие В - в том, что температура окажется в пределах от 18°С до 22°С. Сформулируйте событие AUB.
Желательный результат обсуждения. Удобно изобразить события на координатной прямой:

Объединив события А и В, получим событие «Температура не выше 22°С».
Остальные разработки можно посмотреть по ссылке https://vk.com/urokimatemati4ki
2















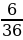 =
= 0,167
0,167






















