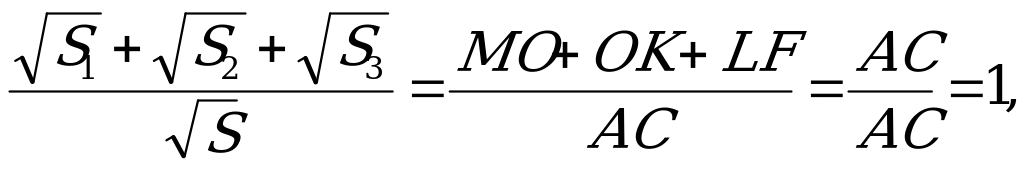Реферат по геометрии
«ПЛОЩАДЬ ТРЕУГОЛЬНИКА»
П л а н .
1.Необходимость измерения площадей в древности и в современной
жизни.
2. Справочная таблица: "Площадь треугольника".
3. Вывод формул площади треугольника, используемых в школьном
курсе геометрии.
4. Понятие о вневписанной окружности.
5. Вывод некоторых формул площади треугольника через элементы
вневписанных окружностей.
6. Примеры решения задач на применение формул площади треугольника.
7. Значение данной темы в развитии представлений о свойствах геометрических фигур.
Зачатки геометрических знаний, связанных с измерением площадей, теряются в глубине тысячелетий.
Ещё 4-5 тыс. лет назад вавилоняне умели определять площадь прямоугольника и трапеции в квадратных единицах. Квадрат издавна служил эталоном при измере- нии площадей благодаря многим своим замечательным свойствам: равные стороны, равные и прямые углы, симметричность и общее совершенство формы. Квадраты легко строить, ими можно заполнить плоскость без пробелов1.

 Древние египтяне 4000 лет назад пользовались почти теми
Древние египтяне 4000 лет назад пользовались почти теми
же приемами, что и мы, для измерения площади прямоугольни-
ка, треугольника и трапеции: основание треугольника дели- а
л ось пополам и умножалось на высоту; для трапеции же сумма
ось пополам и умножалось на высоту; для трапеции же сумма
параллельных сторон делилась пополам и умножалась на d
высоту. Для вычисления площади S четырехугольника со b
с торонами а, b, c, d (рис.1) применялась формула
торонами а, b, c, d (рис.1) применялась формула
c
S = 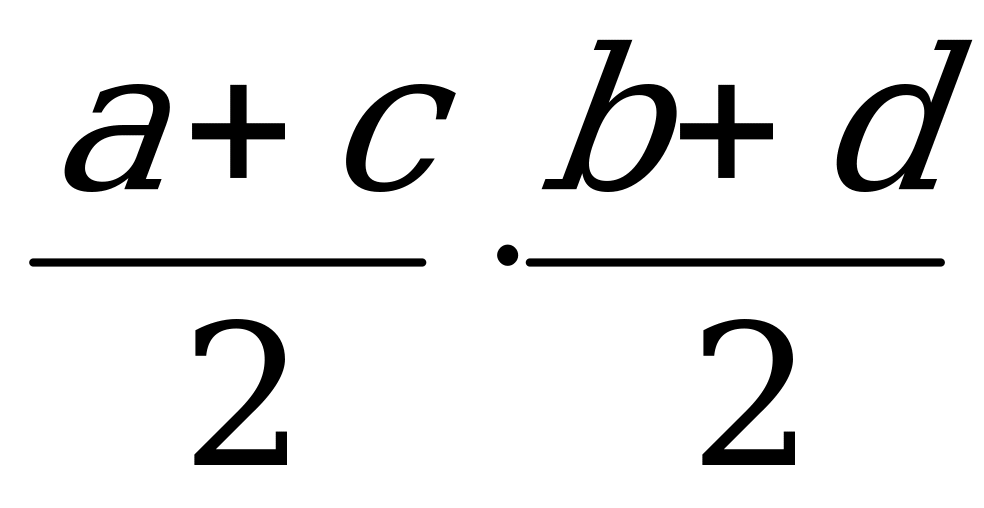 , (1) (рис. 1)
, (1) (рис. 1)
т. е. умножались полусуммы противоположных сторон. Эта формула верна только для прямоугольника. С её помощью можно вычислить приближённо площадь таких четырёхугольников, у которых углы близки к прямым.
Для определения площади S равнобедренного треугольника АВС, в котором
АВ = АС, египтяне пользовались приближённой формулой:
S = 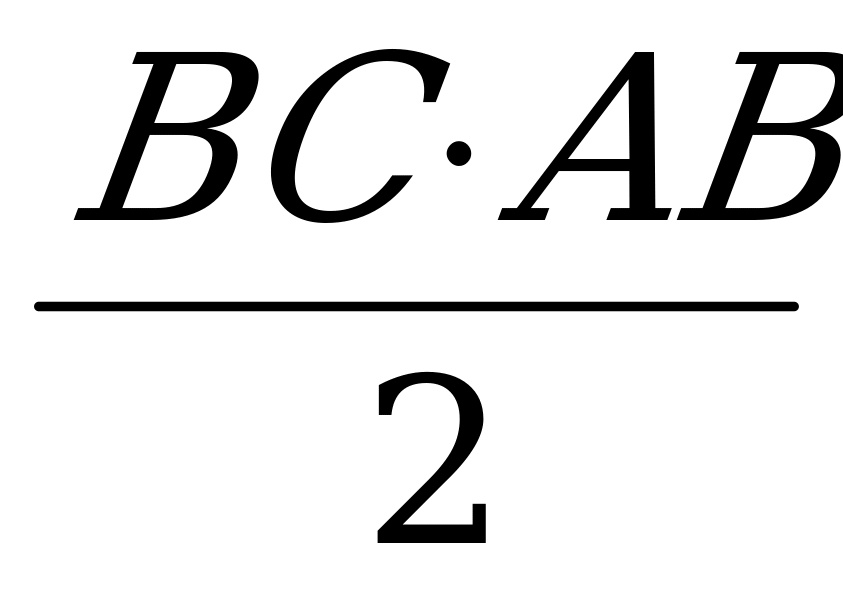 . (2)
. (2)
Совершаемая при этом ошибка тем меньше, чем меньше разность между стороной АВ и высотой АD треугольника , иными словами, чем ближе вершина В ( и С ) к основанию В высоты из А. Вот почему приближённая формула (2) применима лишь для треугольников с сравнительно малым углом при вершине.
Потребность измерения расстояний и площадей приве-
л

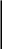

 а к созданию и на Руси рукописей геометрического содержа-
а к созданию и на Руси рукописей геометрического содержа-
ния чисто практического характера. Первые сведения о таких
рукописях относятся к XVI в. Спустя столетие, в 1629 г., а а2  а2
а2
в





 сохранившейся рукописи «Книга сошного письма» имеется а
сохранившейся рукописи «Книга сошного письма» имеется а 
глава «О земном верстании, как земля верстать». В этой главе (рис. 2)
собраны правила измерения площадей фигур различной кон-
фигурации и приведён ряд примеров, как этими правилами S=a2+ a2=
a2=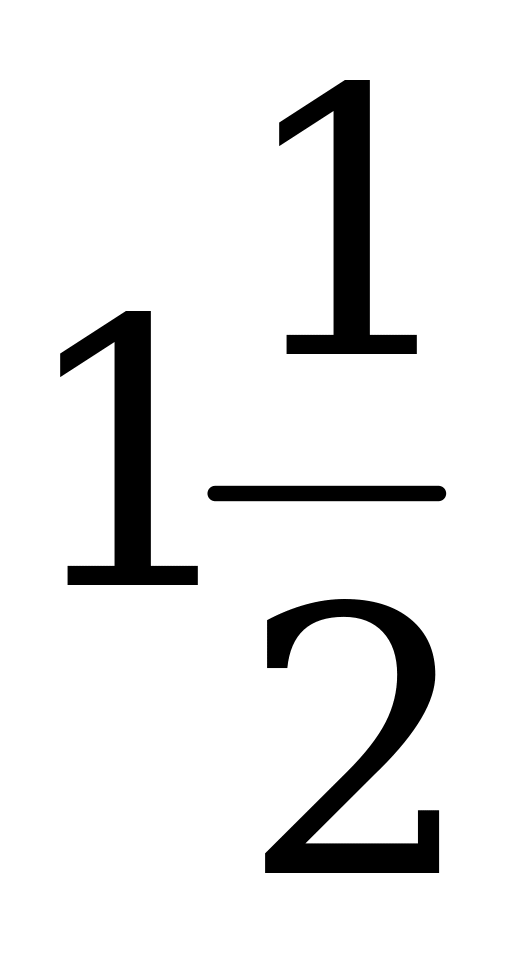 a2
a2
пользоваться. Но выводов и обоснований указанных правил
нет. В рукописи рекомендуется производить измерение и вы-
числение площадей различных фигур посредством измерения площадей простейших
фигур: квадрата, прямоугольника, треугольника и трапеции. Площадь прямоуголь-ника согласно указаниям в этой рукописи следует вычислять путём выделения из
прямоугольника наибольшего квадрата, а площадь оставшегося после отсечения
квадрата прямоугольника вычислить, узнав, какую долю наибольшего квадрата составляет его площадь, посредством сравнения длины стороны квадрата и малого прямоугольника (см. рис.2, на котором обозначения даны современные).
Для вычисления площади треугольника в рукописи рекомендуется произведение большей и меньшей сторон разделить на два. Это правило даёт лишь приближённое значение истинного размера площади.
Из сказанного можно заключить, что точного измерения и вычисления площадей
треугольников и трапеций составители этой рукописи не знали.
Вопреки сохранившимся рукописям создание «русскими мастерами каменных
дел» различных грандиозных сооружений (кремлёвских стен и башен, храмов)
говорит о том что эти мастера обладали довольно основательными знаниями в области геометрии. Без таких знаний сооружение прекрасных зданий, как храм Василия Блаженного в Москве, вряд ли можно совершить.
В своей практической деятельности человек часто имеет дело с площадями.
Чтобы найти, например, урожайность с 1 га, надо знать площадь поля и сколько всего зерна собрано с этого поля. О площади, занимаемой каким - либо государством, мы узнаём из курса географии. Площадь поверхности стен в помещении нужно знать, например, для того, чтобы рассчитать необходимое для их покрытия количество краски, обоев или кафеля. Площадь поверхности дороги нужно знать, например, при расчёте необходимого для её покрытия количества асфальта. Что же такое площадь и как её находить? Чтобы упростить задачу, мы будем сначала рассматривать простые фигуры. Фигуру будем называть простой,
если её можно разбить на конечное число треугольников.
Для простых фигур площадь – это положительная величина, численное значение которой обладает следующими свойствами:
1) Равные фигуры имеют равные площади.
2) Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей её частей.
3) Площадь квадрата со стороной, равной единице измерения, равна единице.
Какие же единицы используются при изменении площадей?
Если сторона квадрата 1 см, то его площадь 1 см2; если сторона квадрата 1 дм, то площадь 1 дм2. А 1 м2 – это площадь квадрата со стороной 1 м, 1 км2 – это площадь квадрата со стороной 1 км... Употребляются и такие единицы площади, как 1 гектар (1 га), 1 ар. 1 га – это площадь квадрата со стороной 100 м, а 1 ар – квадрата со стороной 10 м. 1 ар часто называют соткой. Она содержит 100 м2; например, говорят: «Дачный участок имеет площадь 6 соток».
В справочной литературе мы находим старинные единицы площадей: 1 акр, 1 десятина.
Прямое измерение площадей на практике затруднено, поэтому применяются косвенные методы, наиболее употребительным из которых является вычисление площадей по формулам. Некоторые формулы вычисления площадей я приведу в своей работе.
Формулы площади треугольника.





 1. S =
1. S = 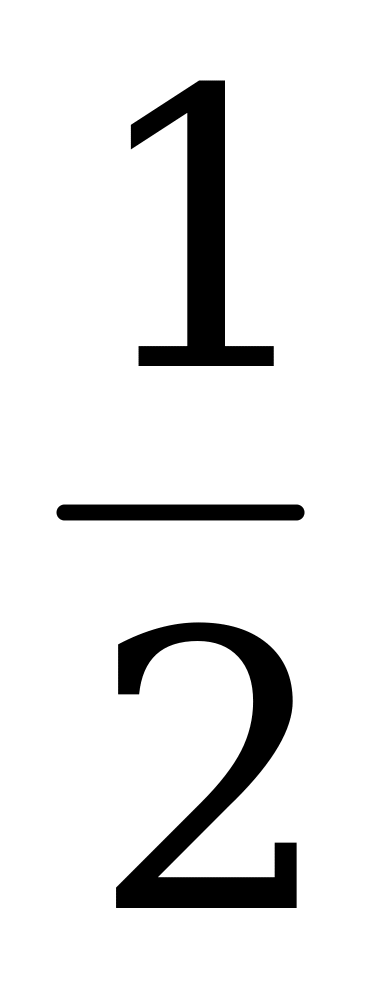 aha
aha
2. S = 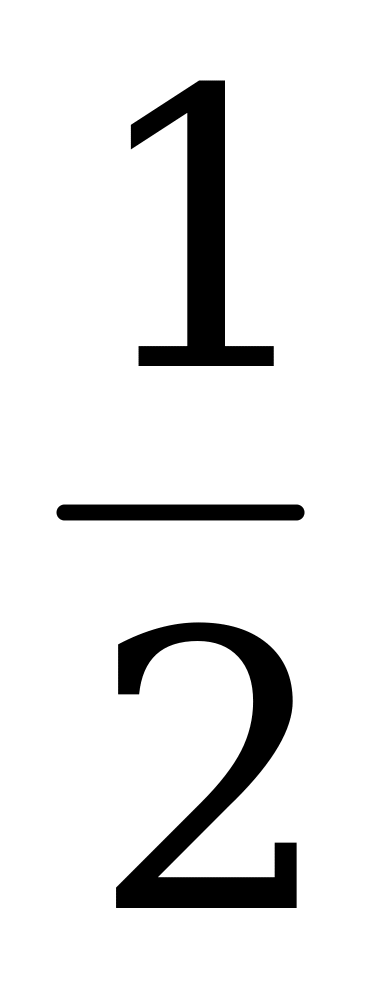 ab sin
ab sin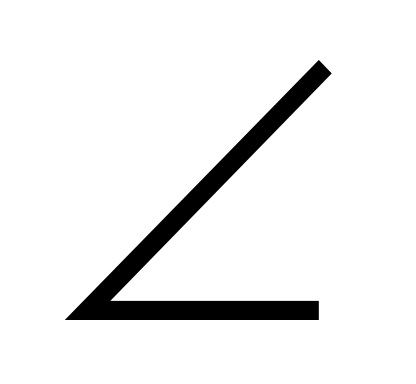 C
C
 3. S = p r
3. S = p r
 4. S =
4. S =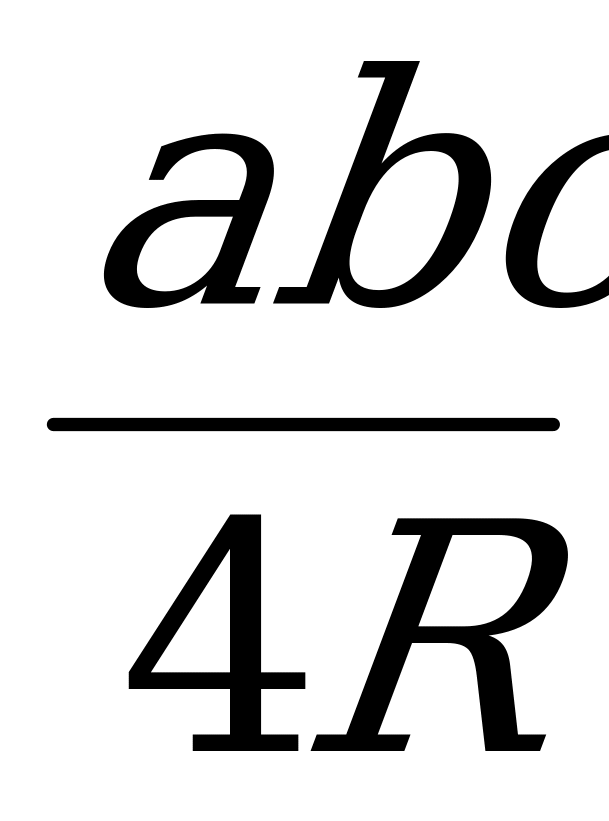
 5. S =
5. S =  , p=
, p=

 6. S =
6. S = 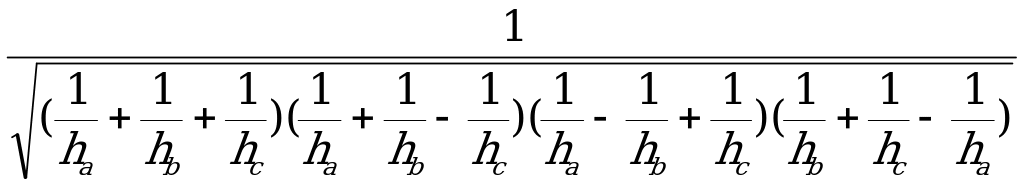
7. S = 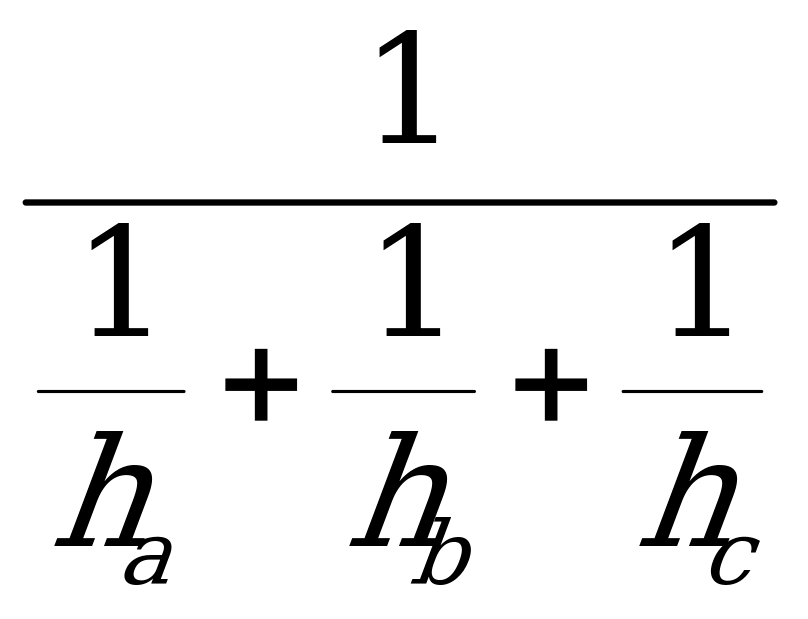

 8. S =
8. S = 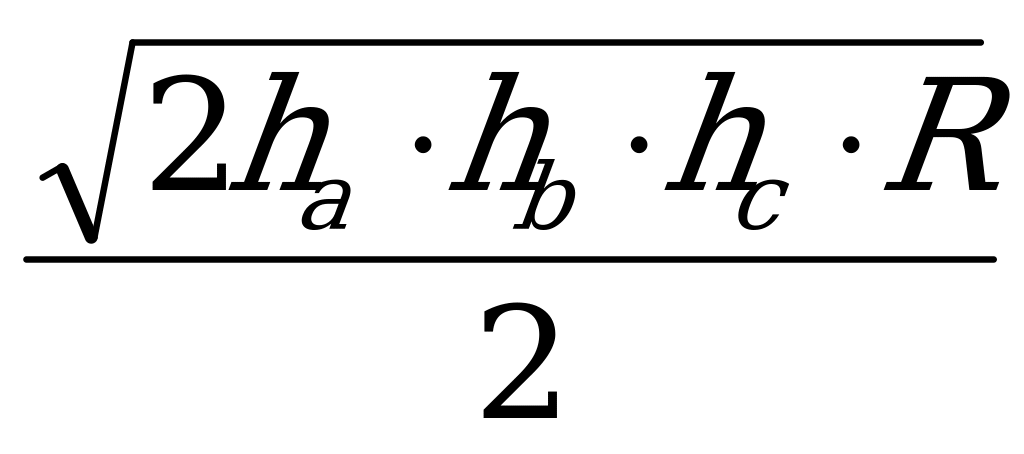
 9. S =
9. S = 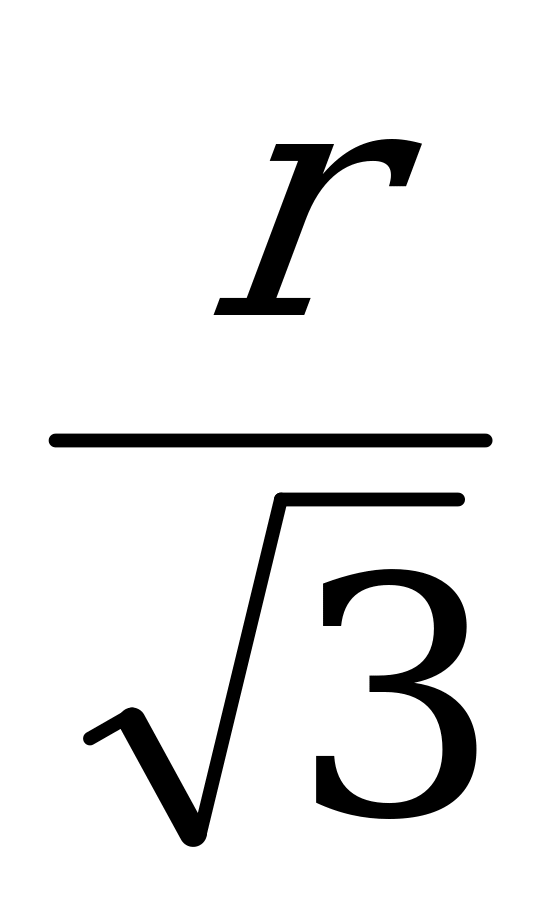 (ha+hb+hc)
(ha+hb+hc)
10. S = 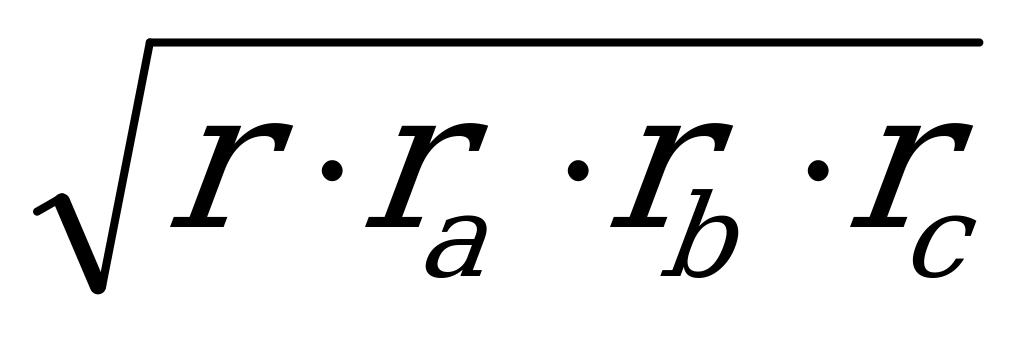 , ra , rb , rc – радиусы
, ra , rb , rc – радиусы
вневписанных окружностей.
 11. S = ra(p – a) = rb(p – b) = rc(p – c)
11. S = ra(p – a) = rb(p – b) = rc(p – c)
 12. S =
12. S = 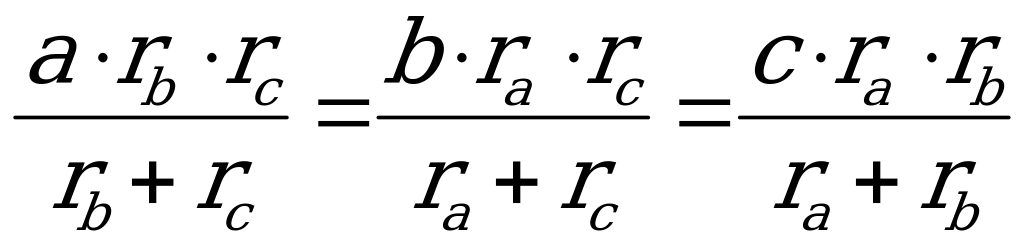
 13. S =
13. S = 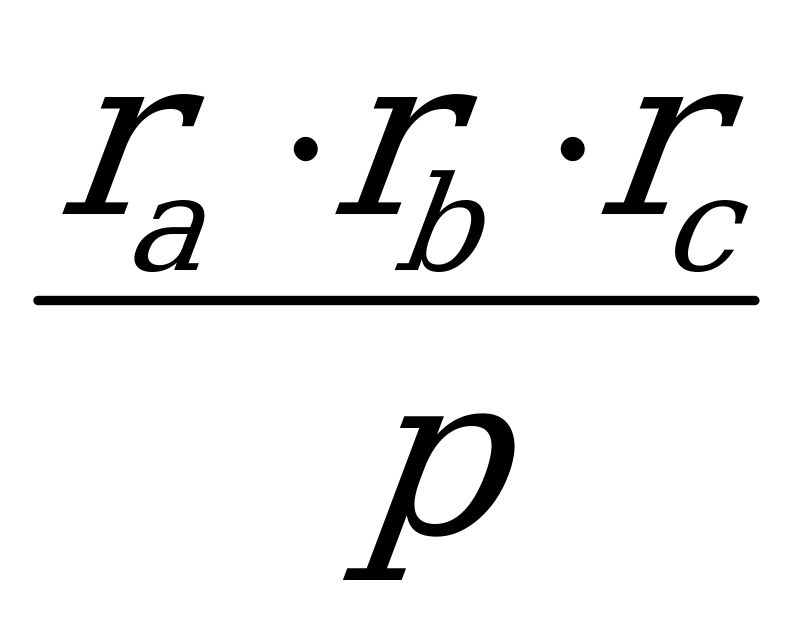
 14. S =
14. S =

15. S = 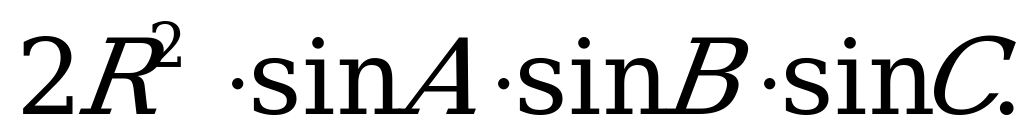

Площадь треугольника
Условимся одну из сторон треугольника называть основанием, а перпендикуляр, проведённый из противоположной вершины к прямой, содержащей эту вершину,- высотой.
Выведем несколько формул площади треугольника, часто используемых при решении задач.
Теорема 1.
Площадь треугольника равна половине произведения
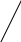

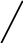

 его основания на высоту. А К
его основания на высоту. А К
Доказательство. Пусть АВС – данный треугольник,
а S - его площадь (рис. 3). Достроим треугольник h
АВС до параллелограмма. Площадь параллелограмма
А КВС равна сумме площадей треугольников АВС и С D a B
КВС равна сумме площадей треугольников АВС и С D a B
АВК. Так как эти треугольники равны, то площадь
параллелограмма равна удвоенной площади треуголь- (рис. 3)
ника АВС : SАКВС = 2S = ah, так как высота паралле-
лограмма, соответствующая стороне ВС, равна высоте треугольника АВС, прове-дённой к стороне ВС. Поэтому



S =  ah , (1)
ah , (1)

где ВС = а, AD = h. Теорема доказана.
Cледствие 1. Площадь прямоугольного треугольника равна половине произведения его катетов.
Следствие 2. Треугольники, имеющие равные основания и равные высоты, равновелики.
Теорема 2.
Площадь треугольника равна половине произведения двух сторон на синус угла между ними .
Доказательство. Проведём в треугольнике АВС высоту
B

 D (рис.4,а). Имеем: S=
D (рис.4,а). Имеем: S=  АС
АС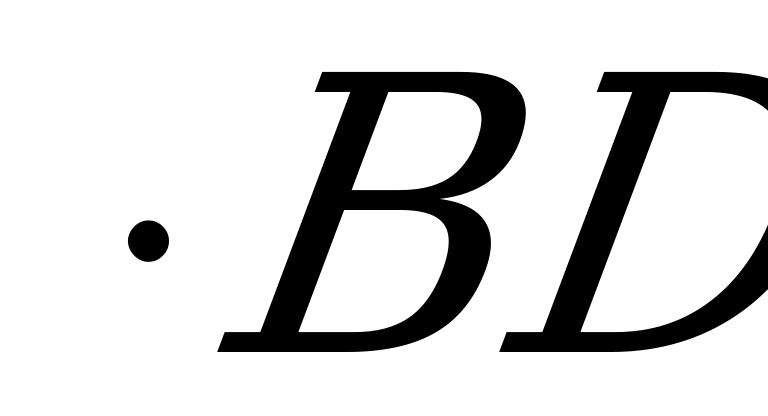 . Из прямоугольного B
. Из прямоугольного B
треугольника ABD : BD = AB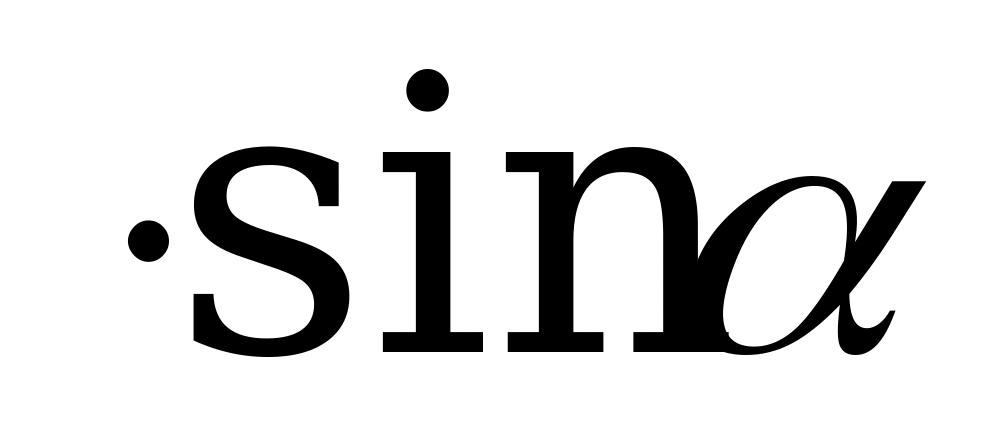 , если угол
, если угол 
острый (рис.4, а), BD = AB (
( -
- ), если угол
), если угол
 тупой (рис.4,б). Так как sin a
тупой (рис.4,б). Так как sin a
(
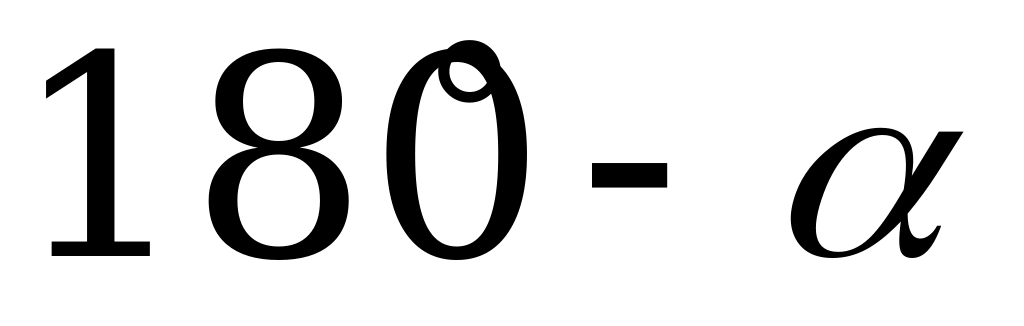 ) = sin
) = sin , то в C D А
, то в C D А
любом случае BD = AB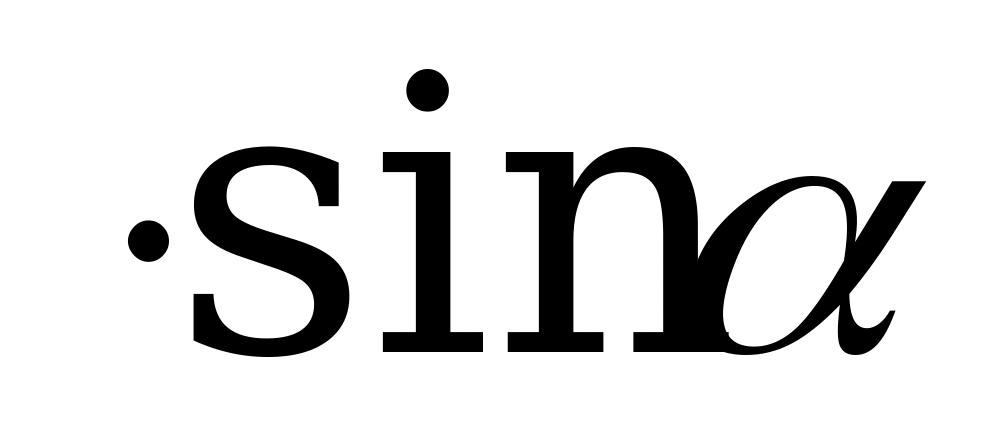 .Следовательно, площадь (рис. 4, а)
.Следовательно, площадь (рис. 4, а)
т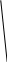
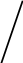
 реугольника S =
реугольника S =  AC
AC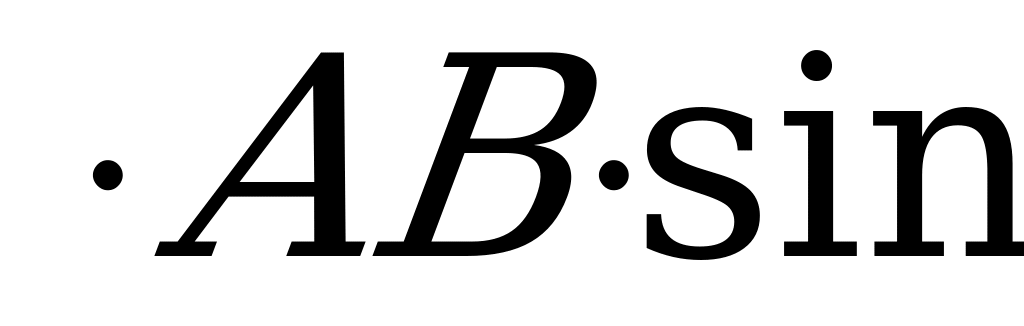 A. В
A. В




S =  bс
bс C . (2)
C . (2)



 а
а
С А D
(рис. 4, б)
Теорема 3.
Площадь треугольника равна произведению его полупериметра на радиус вписанной
о

 кружности:
кружности:
S = pr , (3)
= pr , (3)

г де p =
де p =  (a + b + c). В
(a + b + c). В
Доказательство. Пусть О – центр
окружности, вписанной в треугольник, с а
r – её радиус (рис. 5). Соединив центр r
О с вершинами А, В и С, получим О r
треугольники АОВ, ВОС и АОС с
высотами, равными r. Согласно r r
свойству площадей A b С
(рис. 5)
S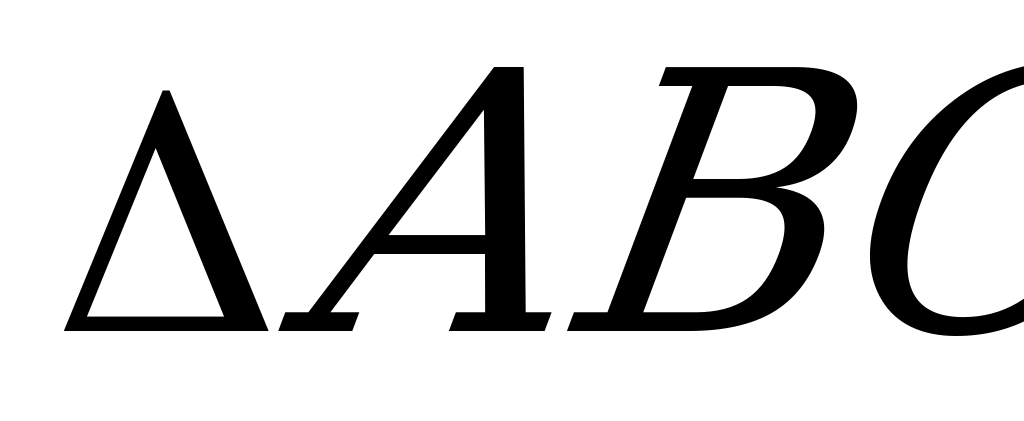 = S
= S + S
+ S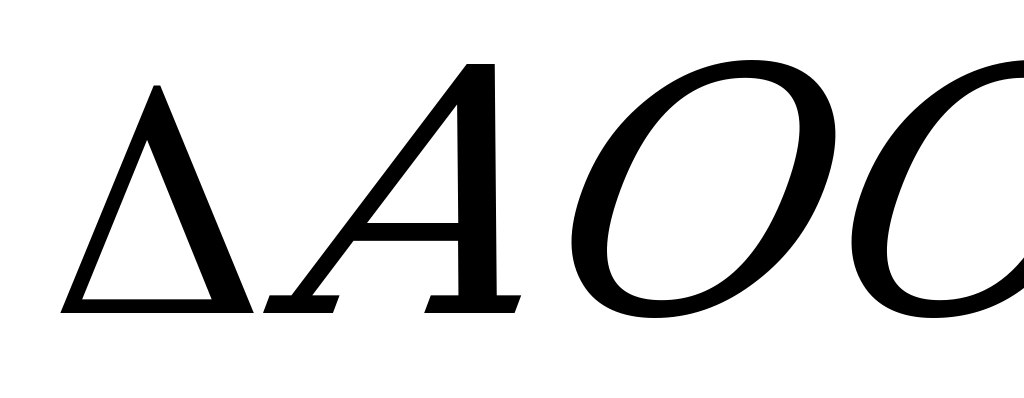 +S
+S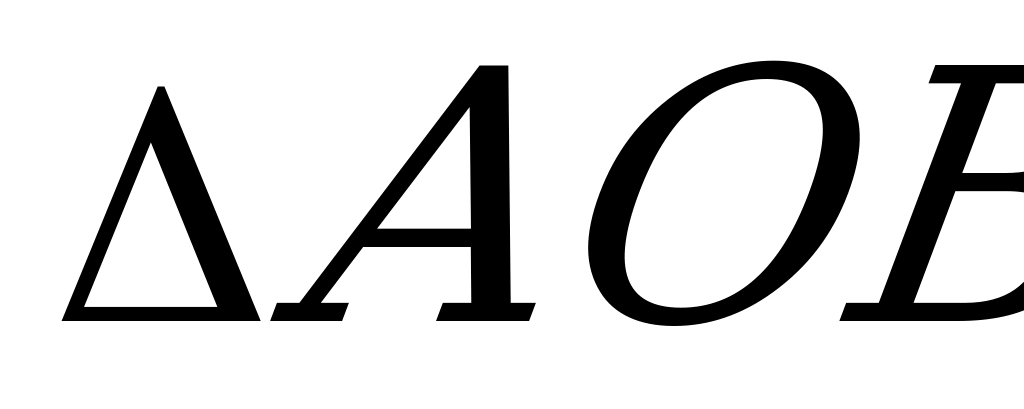 =
=  (a + b + c) = pr,
(a + b + c) = pr,
что и требовалось доказать.
Теорема 4.
Площадь треугольника равна произведению всех его сторон, деленному на учетверенный радиус описанной окружности
S

 =
=  . (4)
. (4)

Доказательство. согласно формуле (2)
S =  bс
bс C.
C.
По теореме синусов
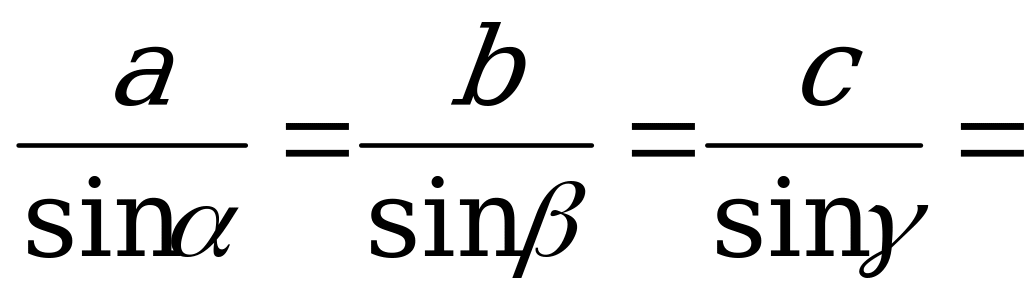 2R,
2R,
где R – радиус окружности, описанной около треугольника. Из равенства

следует, что
sin  =
=  .
.
Подставляя выражение для  в формулу (2), получим
в формулу (2), получим
S =  .
.
Теорема 5.
Формула Герона. Площадь треугольника




S = 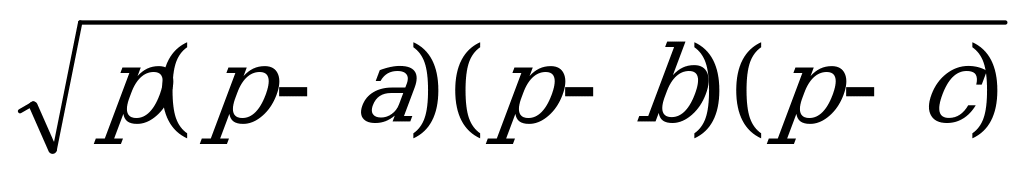 , (5)
, (5)
г де p =
де p =  – половина периметра треугольника.
– половина периметра треугольника.
Доказательство. Из формулы S =  bc
bc C находим
C находим
sin =
=  ;
;
по теореме косинусов a2 = b2 + c2 – 2bc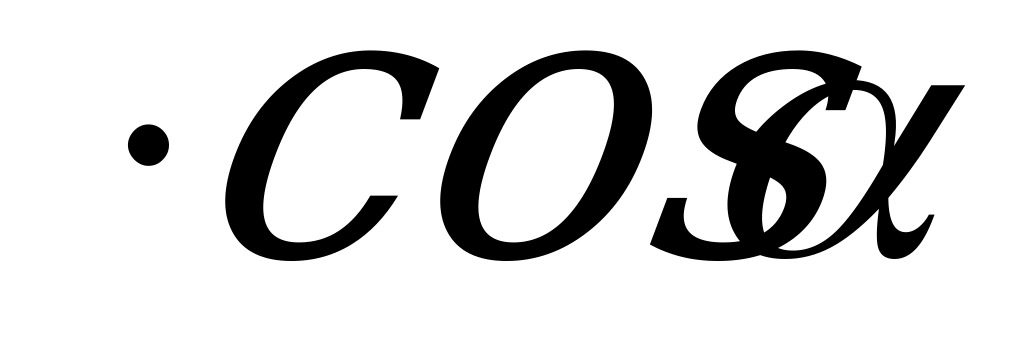 , или
, или
 .
.
Используем основное тригонометрическое тождество 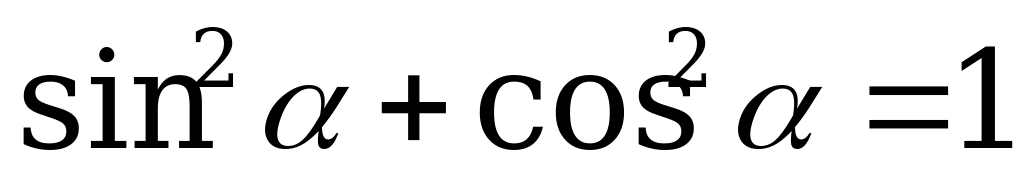 . Получим
. Получим
 .
.
Отсюда, применяя формулу для разности квадратов, имеем
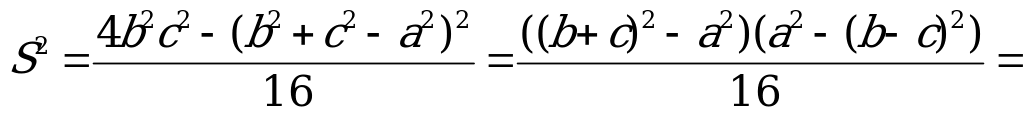
 ;
;
S = 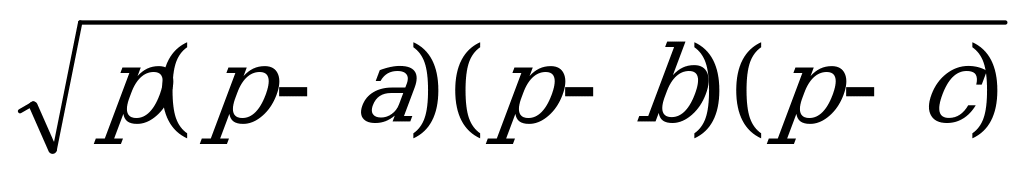 .
.
Формула Герона позволяет вычислить площадь треугольника по его трём
сторонам. Итак, для вычисления площади треугольника получены формулы (1) – (5).
Формулы (3) и (4) можно использовать для вычисления радиусов вписанной и
описанной окружностей, если известны стороны треугольника. Тогда его площадь
можно вычислить по формуле Герона, а затем найти 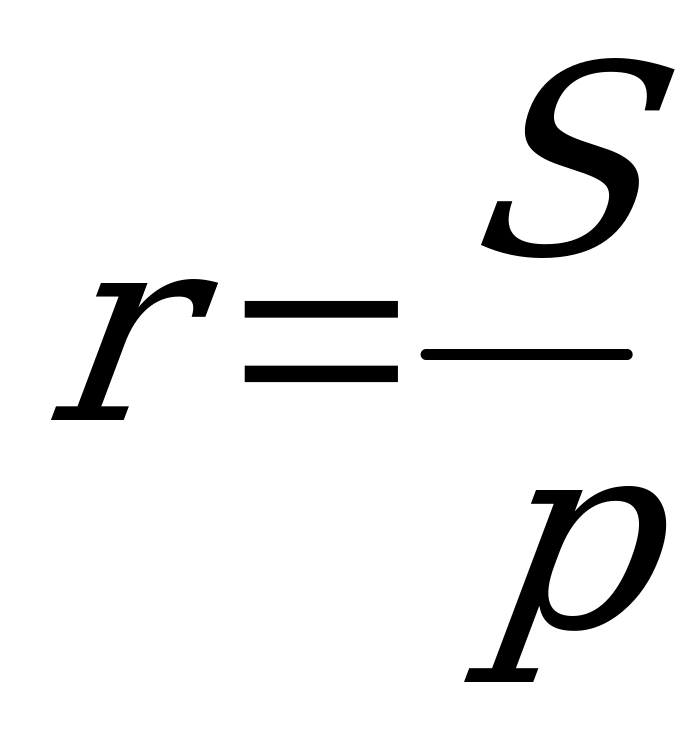 ,
, 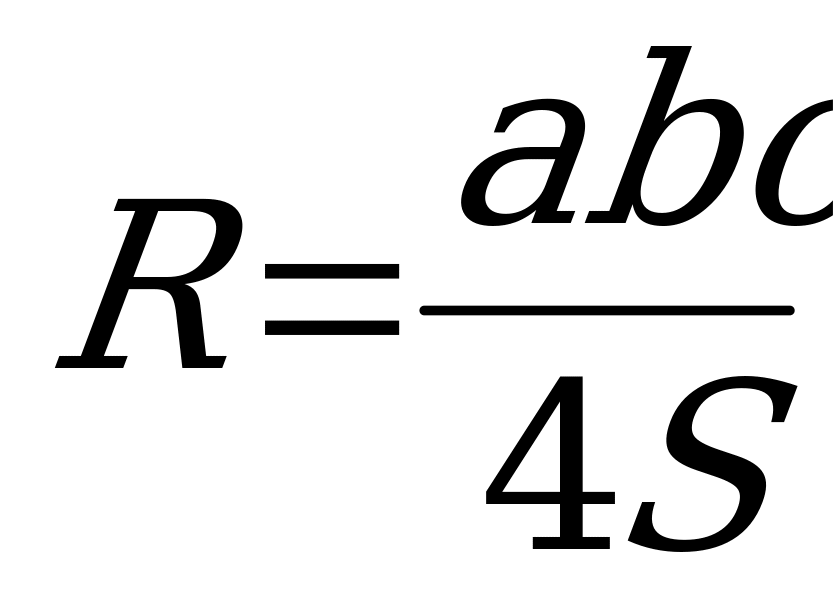 .
.
ВНЕВПИСАННАЯ ОКРУЖНОСТЬ.
Решение некоторых типов геометрических задач, и, прежде всего задач на построение, связано с использованием этого понятия.
Опр. Вневписанной окружностью треугольника называется окружность, касающая-ся одной из его сторон и продолжений двух других.
Для каждого треугольника существует три вневписанных окружности, кото-рые расположены вне треугольника, почему они и получили название вневписанных.
Выясняется, что центрами вневписанных окружностей являются точки пересечения биссектрис внешних углов треугольника. Рассматривая рисунок, замечаем, что центром окружности, вписанной в угол А, служит точка Оа (точка пересечения биссектрис внешних углов треугольника, не смежных с углом А); радиус этой окружности есть отрезок перпендикуляра, проведённого из точки Оа
к





















 какой-либо стороне (или её продолжению):
какой-либо стороне (или её продолжению):
ОаК = ОаК1 = ОаК2 = rа.
K1
ra
rc
Oc  B Oa
B Oa
rc rc ra ra
c a
K
b
A C K2
rb
rb
rb
Ob
(рис. 6)
Аналогично можно найти центры Оb , Ос и радиусы rb , rc двух других вневписан- ных окружностей.
Зная длины сторон a,b,c треугольника АВС, вычислим S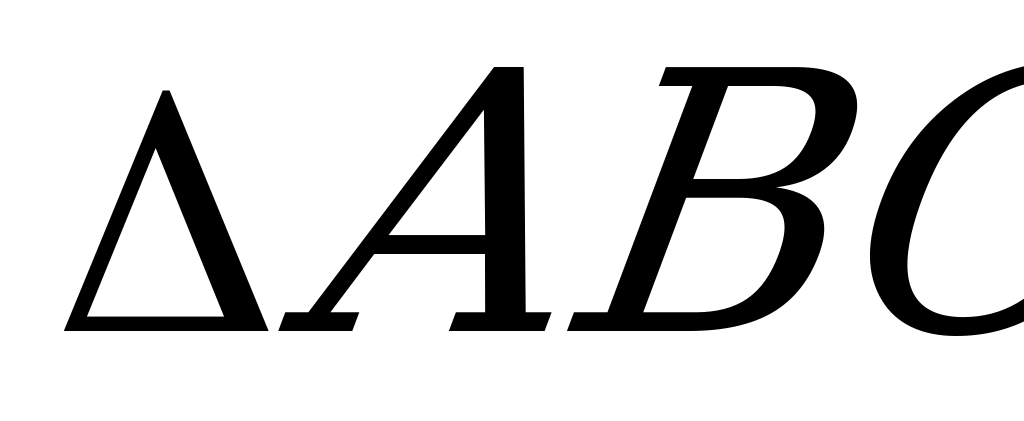 .
.
S
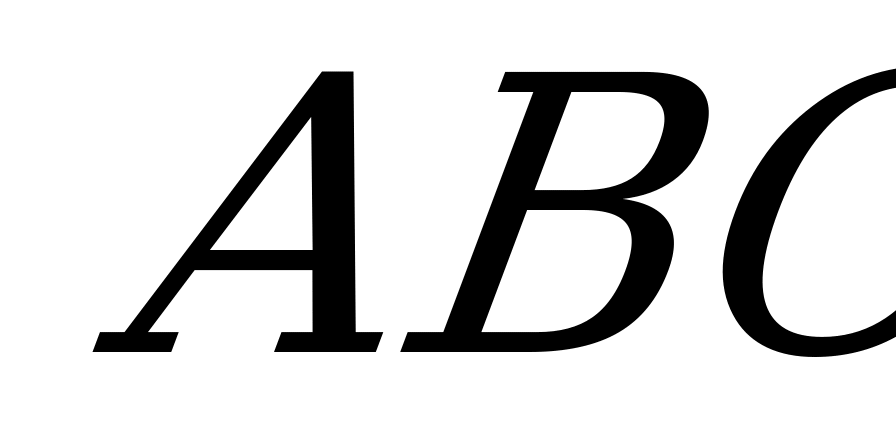 = S
= S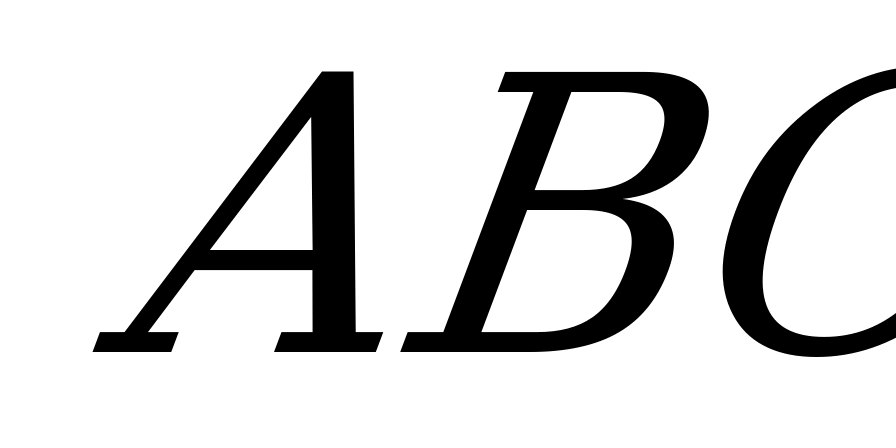 a + S
a + S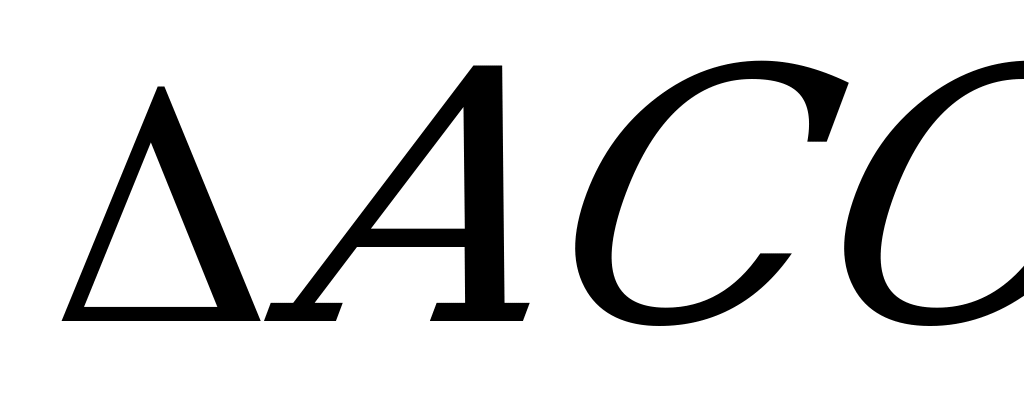 a - S
a - S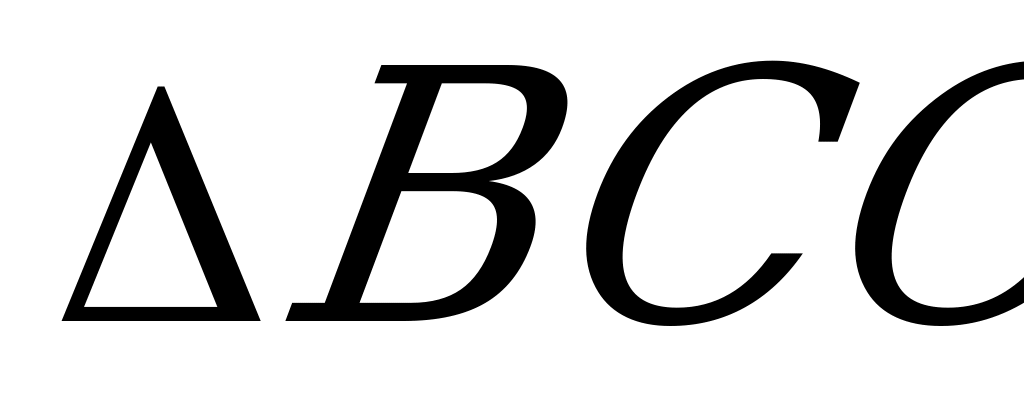 a =
a =  cra +
cra +  bra -
bra -  ara =
ara =

 ra ( c+b-a) = ra ( p –a ).
ra ( c+b-a) = ra ( p –a ).
 Т.е. S = ra (p – a). Таким же образом находим: S = rb(p – a) и S = rc(p –c).
Т.е. S = ra (p – a). Таким же образом находим: S = rb(p – a) и S = rc(p –c).



S = ra(p – a) , S = rb(p – b), S = rc(p – c) ( 6 )

Из формулы ( 6 ) следует, что ra = , r b =
, r b =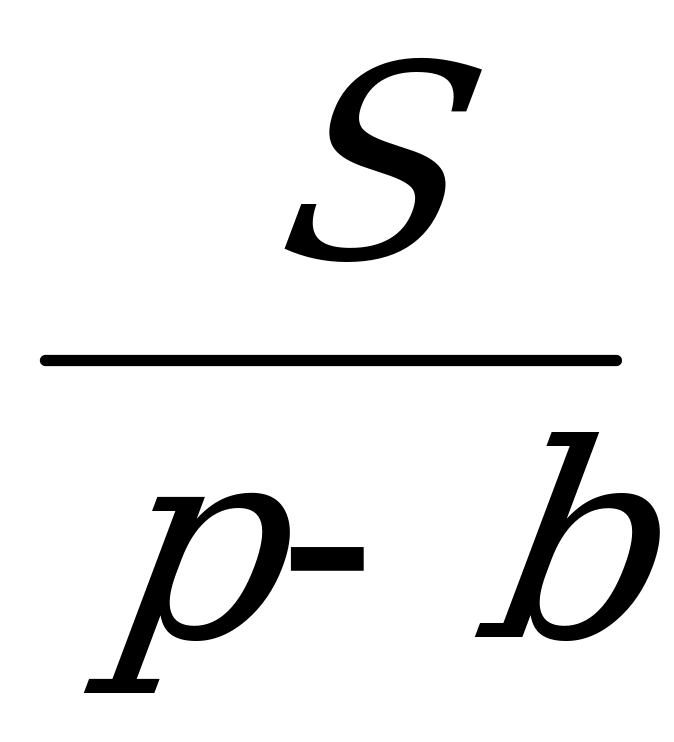 , rc =
, rc =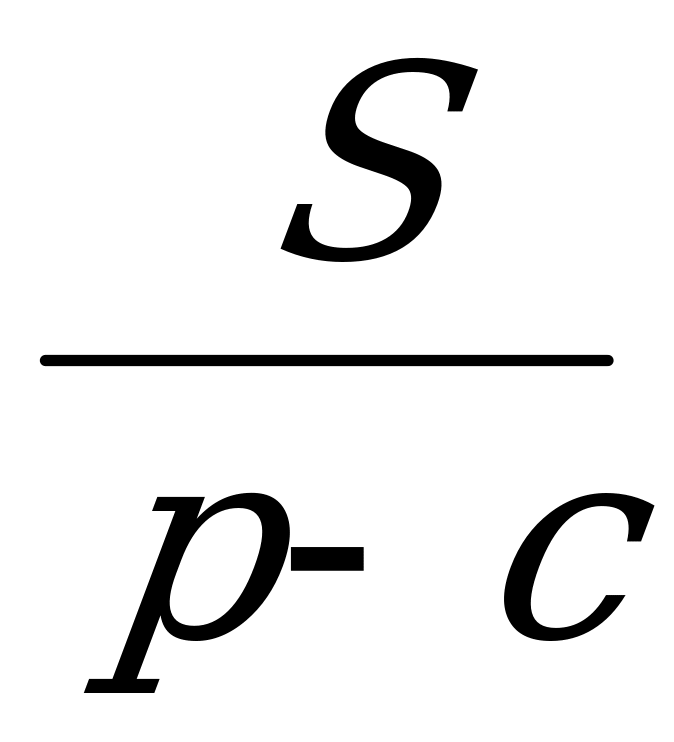 .
.
Найдём произведение ra rb rc.
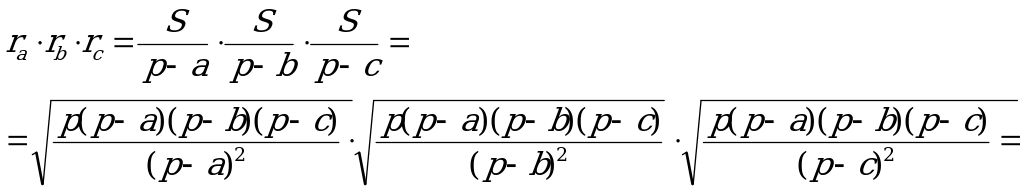

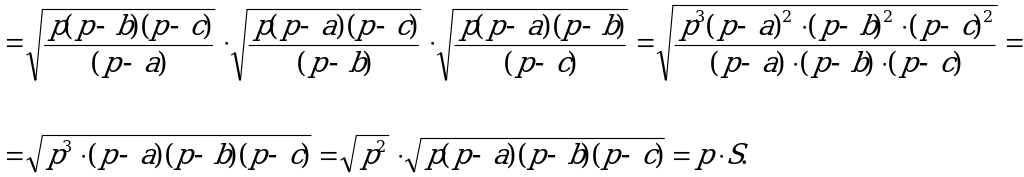
Отсюда следует, что:



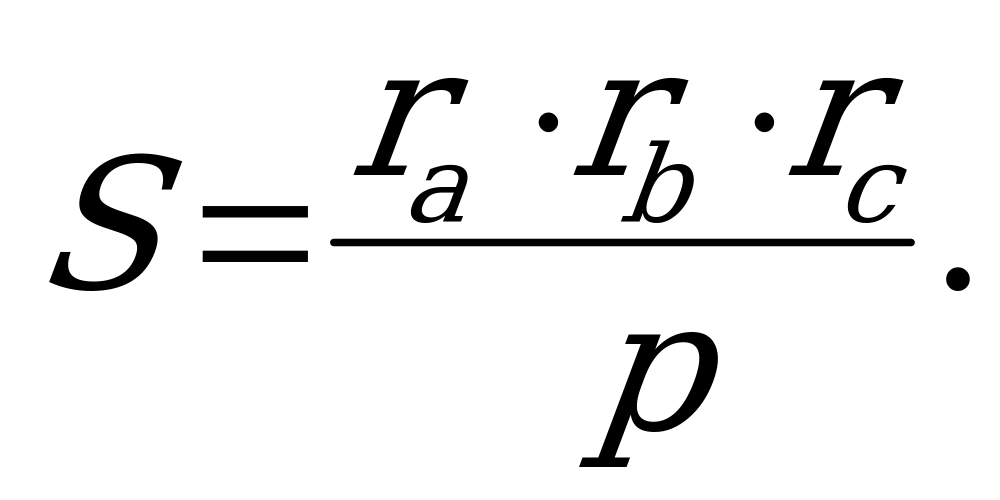 (7)
(7)

Решение задач.
В своей работе я предлагаю серию устных упражнений по готовым чертежам на непосредственное применение формул площади треугольника. Эти задачи допускают различные пути решения. Тем самым подчеркивается, во – первых, что различные
формулы приводят к одним и тем же результатам, и, во – вторых, что необходимо уметь сравнивать различные пути решения и выбирать наиболее рациональные.



Вычислить площадь фигуры





 6
6





 1,5
1,5



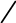
 а 8 см
а 8 см




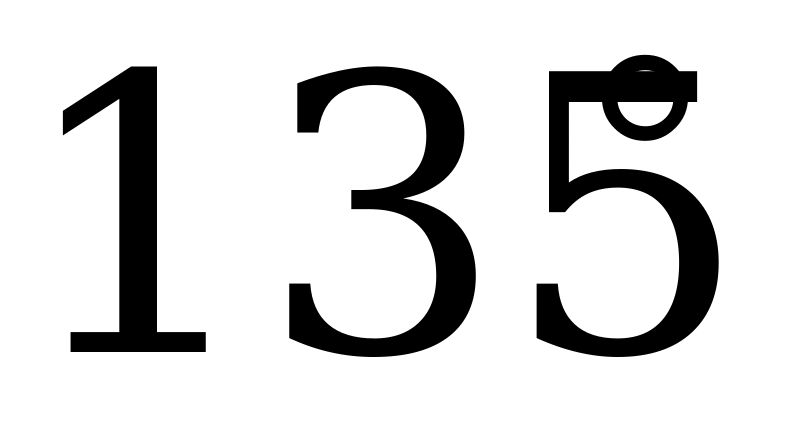
 Правильный
Правильный
шестиугольник

Квадрат



 C
C
12









 а а 5
а а 5
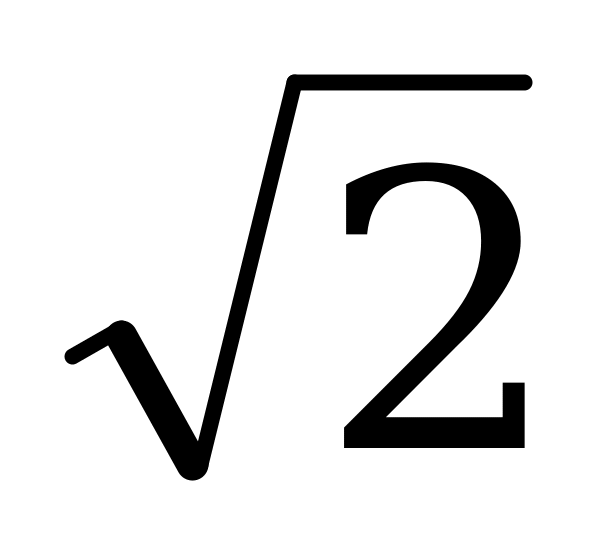 13
13


 Прямоугольник
Прямоугольник










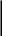




6 8 6 см 
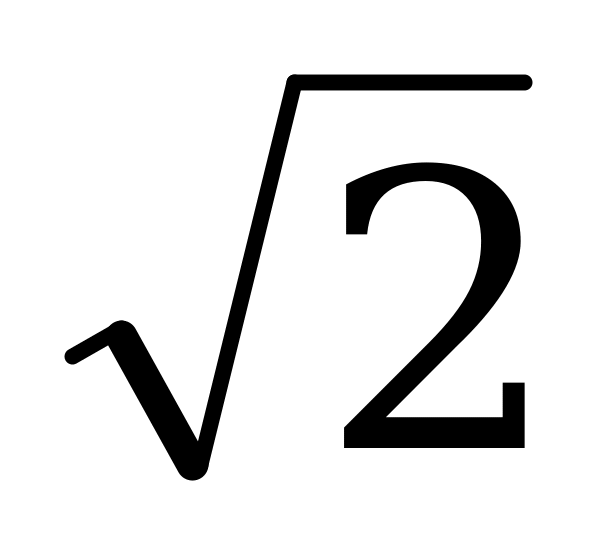







10 R

Рассмотрим примеры на применение формул площади треугольников при решении
различных типов задач.
Задача 1.
Стороны треугольника равны 18см и 10см. Высота к стороне 10см равна 6см. Найти
высоту к стороне 18см.
Дано:  АВС, ВМ и СК – высоты,
АВС, ВМ и СК – высоты,








 В АС = 10см, АВ = 18см, ВМ = 6см.
В АС = 10см, АВ = 18см, ВМ = 6см.
Найти: СК.
Решение.
Найдём площадь треугольника
К 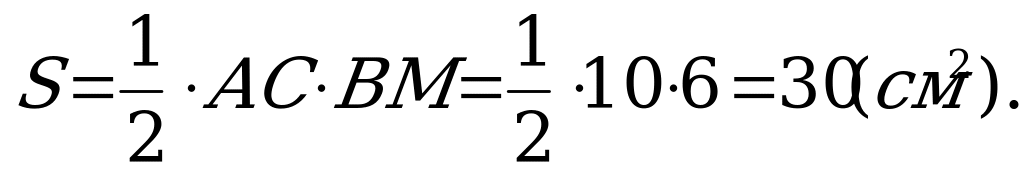
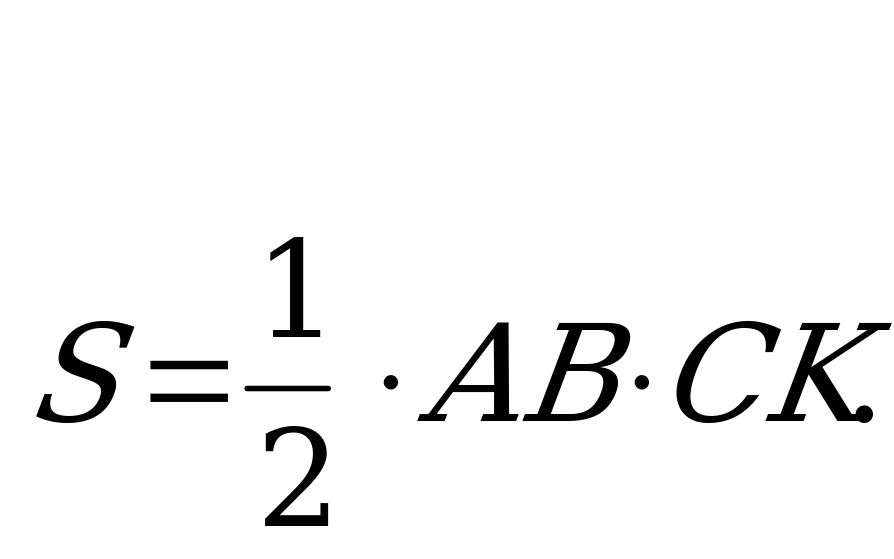 Но площадь можно найти по-другому:
Но площадь можно найти по-другому:
А М C
Подставим в это равенство
(рис. 7)
вместо площади число 30, вместо АВ – число 18 и получим уравнение:
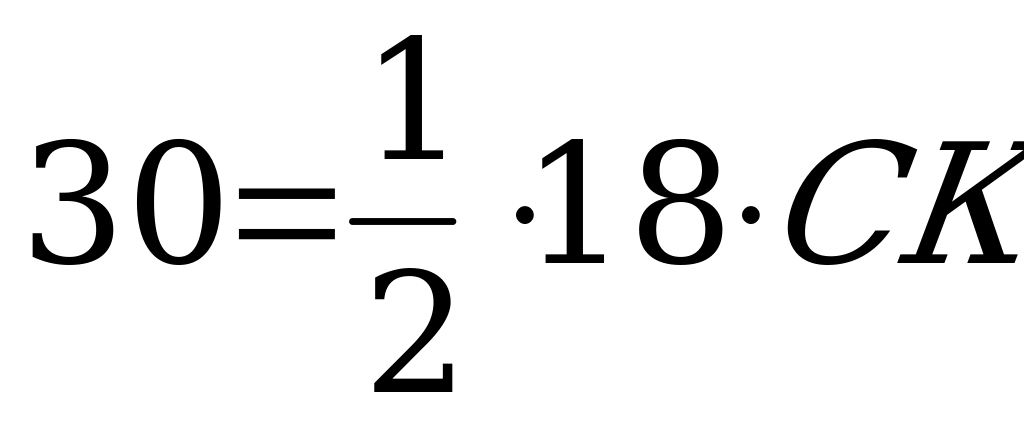 , откуда СК =
, откуда СК = 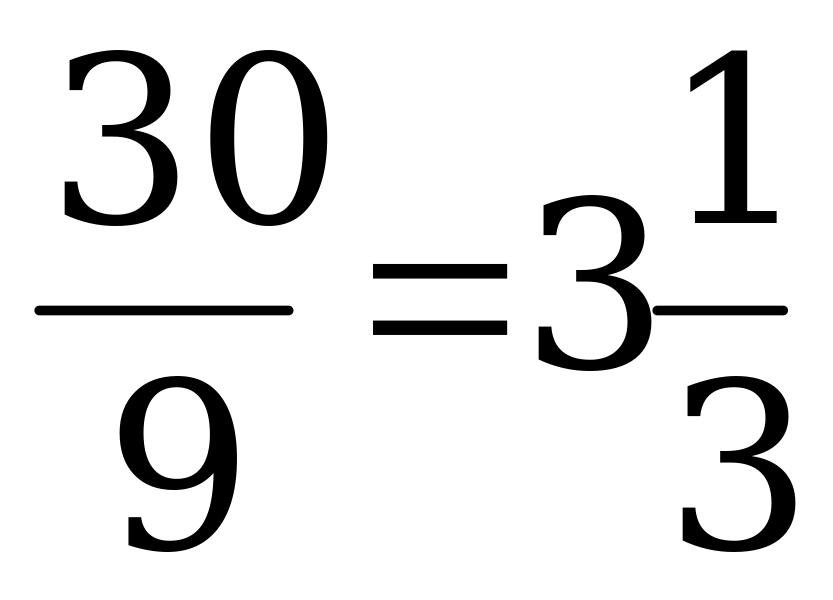 (см).
(см).
Ответ: 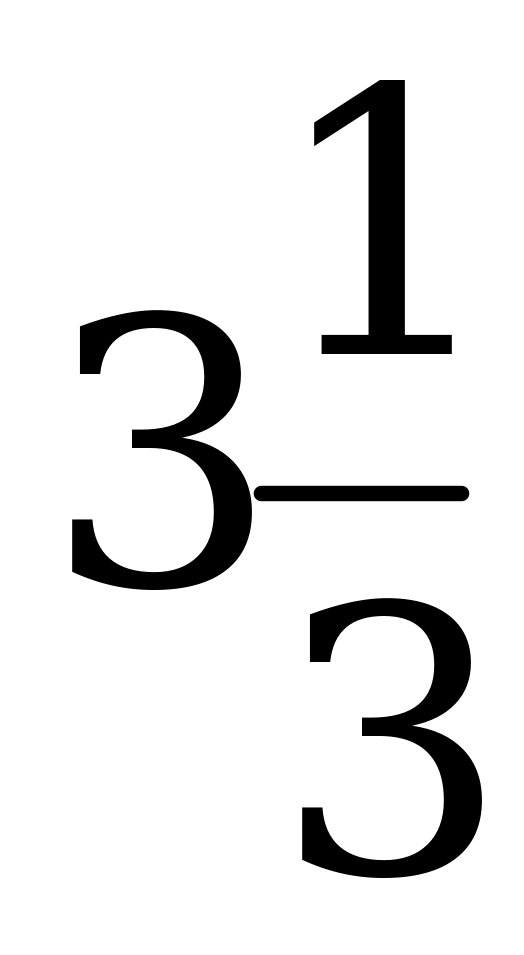 см.
см.
Задача 2.
Стороны треугольника равны 12 см, 16 см, 20 см. Найти радиус описанной окружности.
Д ано: Решение.
ано: Решение.
 АВС со Найдём площадь треугольника по формуле Герона. Она равна 96 см2.
АВС со Найдём площадь треугольника по формуле Герона. Она равна 96 см2.
сторонами
12см,16 см, S =  Подставим данные, получим:
Подставим данные, получим:
20 см. 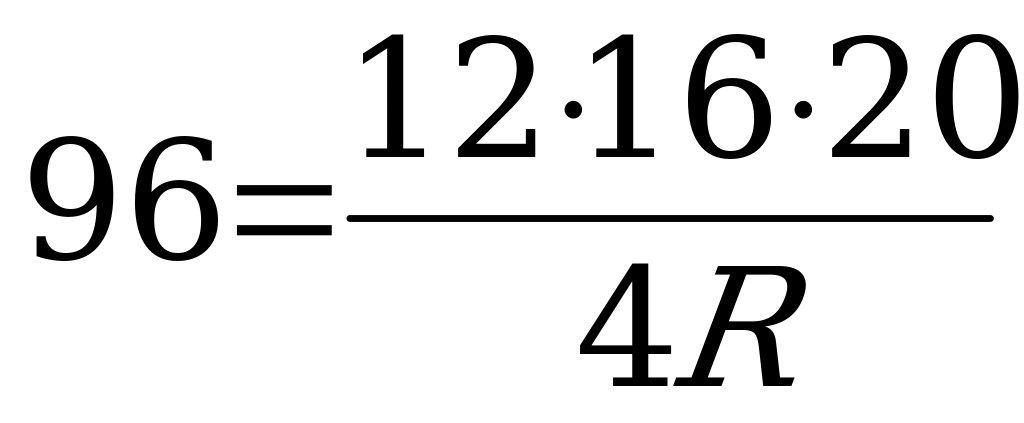 , откуда R=10см.
, откуда R=10см.
Н айти:
айти:
R
Ответ: 10см.
Задача 3.
В угол с вершиной С вписана окружность, отрезок АВ с концами на сторонах угла касается этой окружности, Найти радиус окружности, если известно, что ВС=a, АС=b, АВ=с.
Решение.
Вообще говоря, возможны две ситуации, изображенные на (рис. 8) и (рис. 9). На этих рисунках точка О есть центр заданной окружности, а E, F и G – точки касания
окружности с прямыми СА, АВ и СВ соответственно. В первом случае речь идёт о
выражении радиуса r вписанной в треугольник окружности через его стороны, а во
втором – о выражении радиуса р так называемой вневписанной окружности. Обозна –
чим также буквой S площадь треугольника АВС.


 А
А
Е

 Е
Е
 А
А


 O F О
O F О
F

 C G B C B G
C G B C B G
(рис. 8) (рис. 9)
Рассмотрим сначала первый случай (рис. 8). Радиус, проведённый в точку касания,
перпендикулярен касательной, поэтому отрезки OE, OF и OG – высоты соответствен-
но треугольников АОС, АОВ и ВОС, проведённые из вершины О. Но тогда

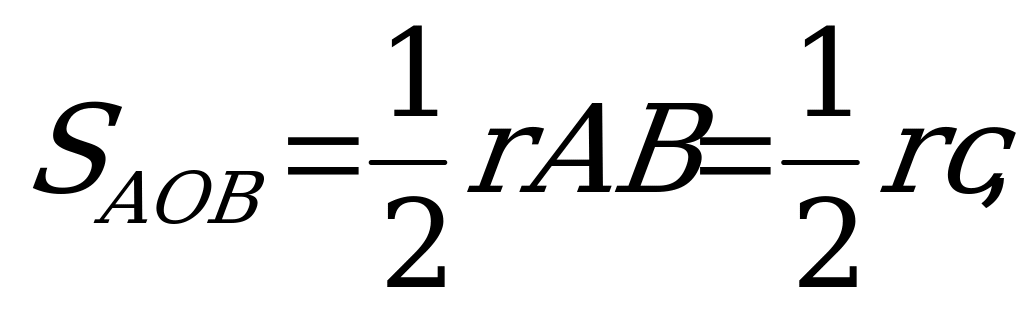

и, значит

где р – полупериметр треугольника АВС. Пользуясь формулой Герона для площади
треугольника, находим искомое выражение
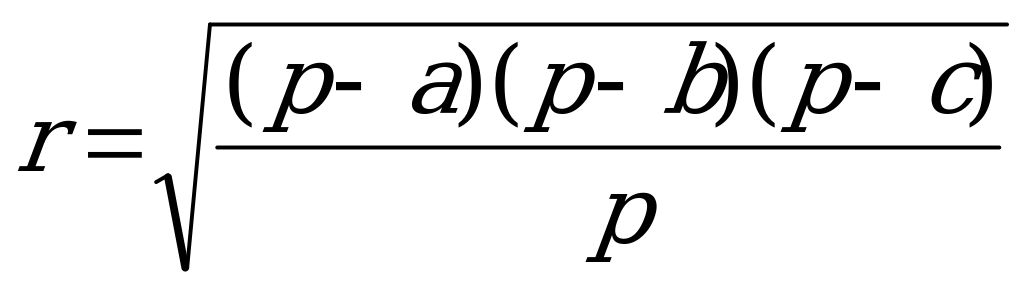 (1).
(1).
Во втором случае (рис. 9), как легко проверить, справедливы те же самые выражения для площадей треугольников АОС, АОВ и ВОС, но в этом случае имеет
место иное соотношение между площадями

из которого находим
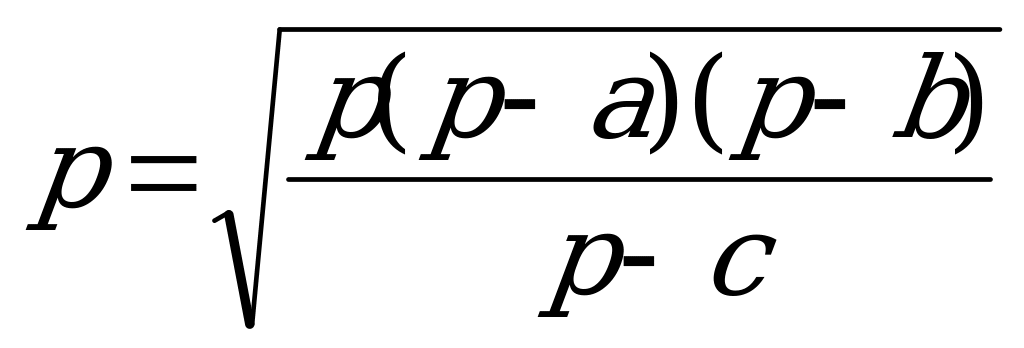 (2).
(2).
Выражения (1) и (2) дают ответ задачи.
* * *
Очень часто на олимпиадах по математике, предлагаются задачи на нахожде-
ние площади треугольника. На решение некоторых из них я хочу остановиться более подробно.
Задача 4.
Разделить треугольник на две равновеликие части прямой, проходящей через данную
точку его стороны.
Решение. Пусть АВС – данный треугольник и М – данная точка на его стороне АС
(рис. 6). Если М – середина стороны АС, то ВМ – медиана и SABM = SBCM. Пусть М не
является серединой стороны АС, например, АМBD, соеди –
ним точки В и М, проведём DN||ВМ. Прямая MN – искомая. В
Д

 окажем это.
окажем это.
Имеем


 N
N
SMNC = SMOD + SDONC.
O
В трапеции BNDM треугольники MOD и BON равновелики:
 A M D C
A M D C
 SMOD + SBOM = SMBD; SBON + SBOM = SMBN, но (рис. 10)
SMOD + SBOM = SMBD; SBON + SBOM = SMBN, но (рис. 10)
SMBD = SMBN , так как треугольники имеют общее основание и равные высоты. Значит,
SMNC = SBON + SDONC = SBDC =  SABC.
SABC.
Задача 5.
Медианы треугольника равны 9см, 12см и 15см. Найти площадь треугольника.
Решение. Пусть АА1, ВВ1, СС1 – медианы
АВС, О – точка их пересечения (рис. 7). Получим шесть
равновеликих треугольников:
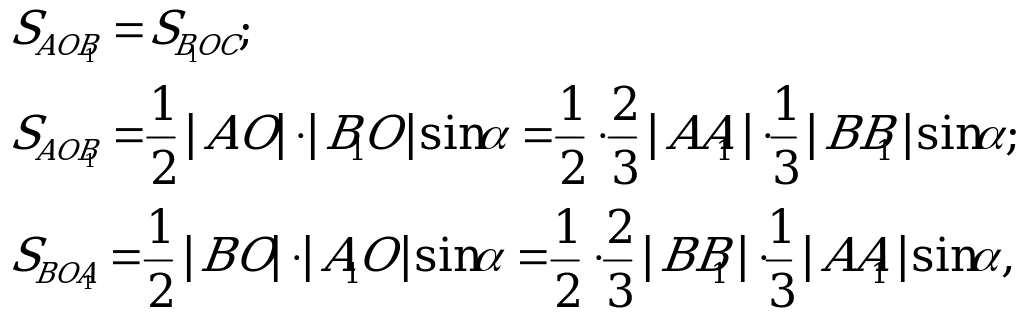


 В следовательно,
В следовательно,  и т.д. Каждая из сторон
и т.д. Каждая из сторон
треугольника СОВ2 равна 2/3 соответствующей медианы
треугольника АВС. Площадь треугольника СОВ2 с дан -

 С1 а А1 ными сторонами можно найти по формуле Герона, а
С1 а А1 ными сторонами можно найти по формуле Герона, а
а О затем найти 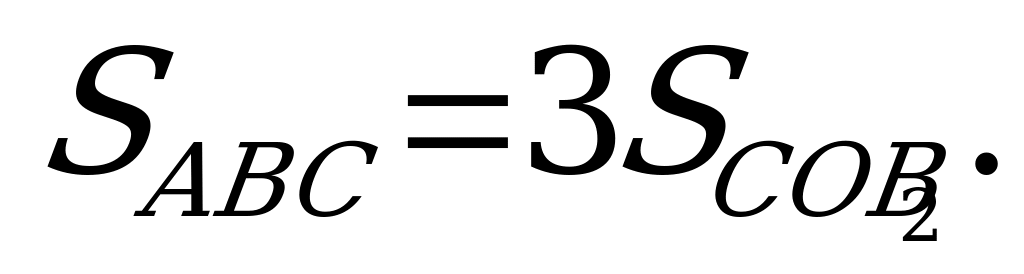


 А В1 С Стороны треугольника СОВ2 равны 6см, 8см и 10см.
А В1 С Стороны треугольника СОВ2 равны 6см, 8см и 10см.
Заметим, что 62 + 82 = 102, и значит, треугольник СОВ2 –
В2 прямоугольный с катетами 6см и 8см. Поэтому
(рис. 11) 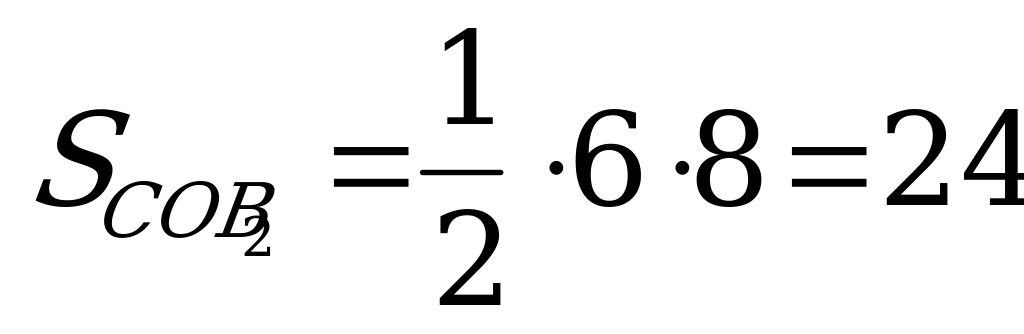 (см2), SABC = 72 (cм2).
(см2), SABC = 72 (cм2).
Ответ: 72см2.
Задача 6.
Через некоторую точку, взятую внутри треугольника проведены 3 прямые, соответственно параллельные сторонам треугольника. Эти прямые разделяют
треугольник на 6 частей, из которых 3 треугольника с площадями S1, S2, S3. Найдите
площадь данного треугольника.
Д ано:
ано:

 АВС, B
АВС, B
NF||BC,
L P||AB, P
P||AB, P
MK||AC,
SMNO = S1,
S OPK = S2, N S2
OPK = S2, N S2
S LOF = S3. M S1 O K
LOF = S3. M S1 O K
Н айти:
айти:
SABC = S. S3
 A C
A C
L F
(рис. 12)
Решение.
1)  MNO~
MNO~ ABC, следовательно
ABC, следовательно 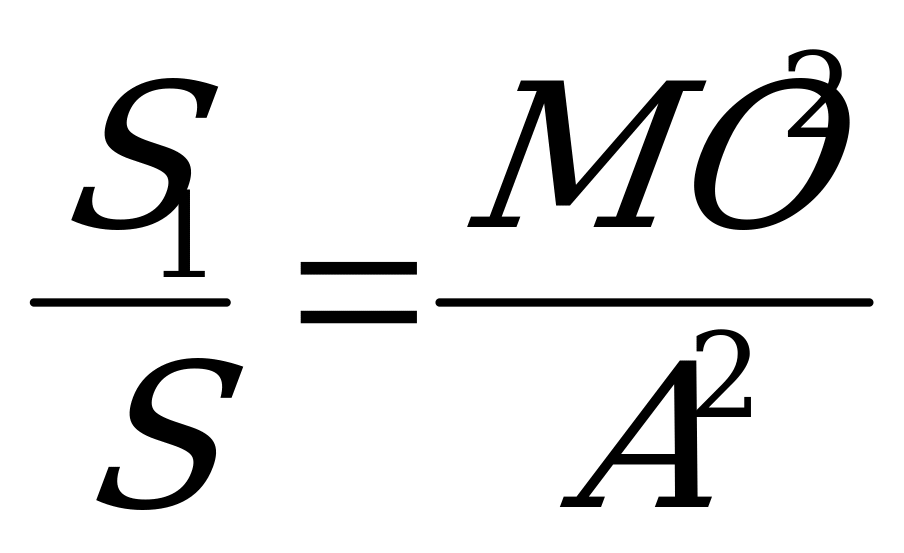 (площади подобных треугольников относятся как квадрат коэффициента подобия).
(площади подобных треугольников относятся как квадрат коэффициента подобия).
2) 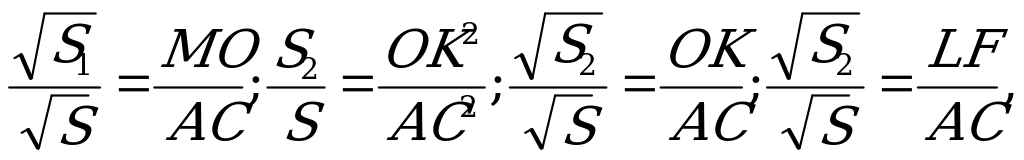
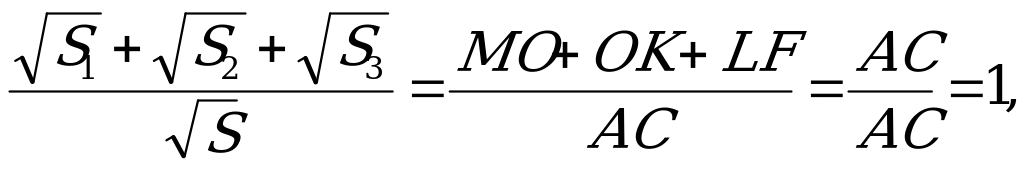
 отсюда
отсюда
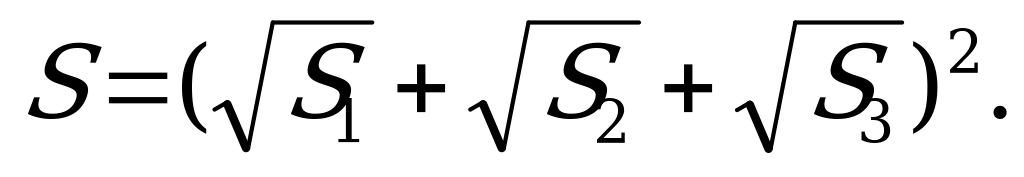
Ответ: 
* * *
Само возникновение геометрии говорит о практической направленности этой науки
("гео" – по-гречески земля, а "метро" – мерить), а понятие площади является основополагающим не только в геометрии, но и в более глубоком понимании окружающего нас мира. Формулы площади треугольника являются основой решения множества геометрических задач, содержат богатейший теоретический материал, позволяющий развивать познавательный интерес, общую культуру и творчество средствами математики и её истории.








 Древние египтяне 4000 лет назад пользовались почти теми
Древние египтяне 4000 лет назад пользовались почти теми  ось пополам и умножалось на высоту; для трапеции же сумма
ось пополам и умножалось на высоту; для трапеции же сумма  торонами а, b, c, d (рис.1) применялась формула
торонами а, b, c, d (рис.1) применялась формула


 а к созданию и на Руси рукописей геометрического содержа-
а к созданию и на Руси рукописей геометрического содержа-

 сохранившейся рукописи «Книга сошного письма» имеется а
сохранившейся рукописи «Книга сошного письма» имеется а 



 1. S =
1. S = 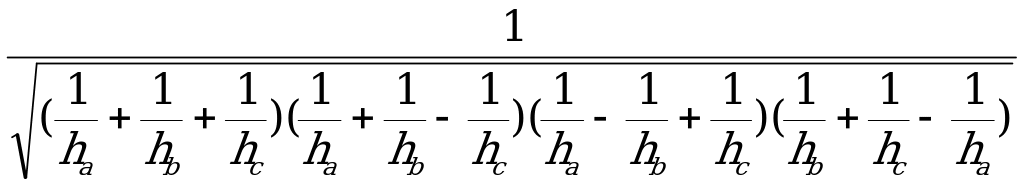
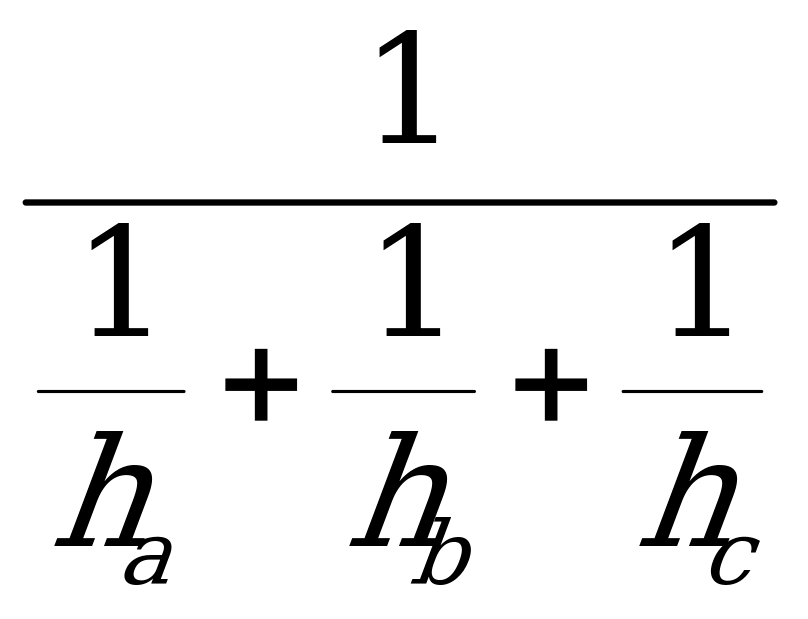



 его основания на высоту. А К
его основания на высоту. А К КВС равна сумме площадей треугольников АВС и С D a B
КВС равна сумме площадей треугольников АВС и С D a B



 D (рис.4,а). Имеем: S=
D (рис.4,а). Имеем: S= 
 реугольника S =
реугольника S = 



 а
а
 де p =
де p = 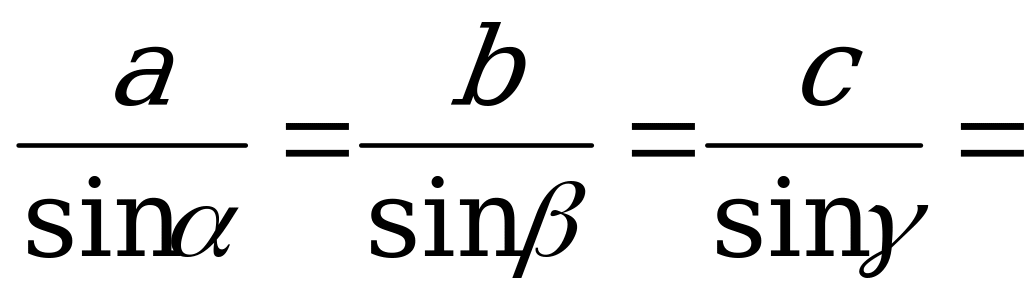 2R,
2R,
 .
. .
.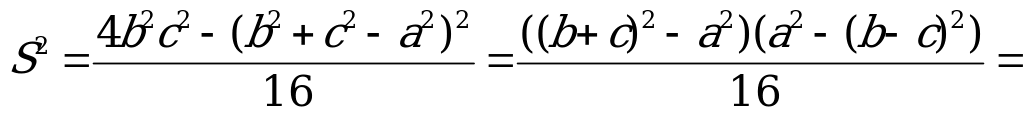




















 какой-либо стороне (или её продолжению):
какой-либо стороне (или её продолжению): B Oa
B Oa 
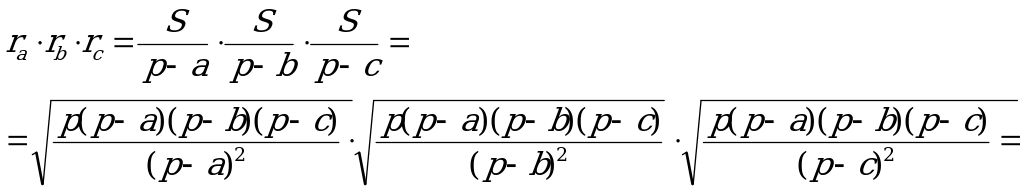
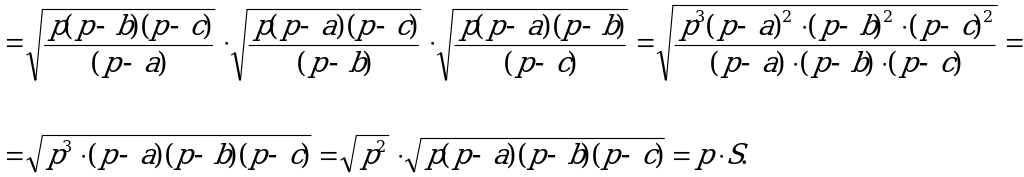
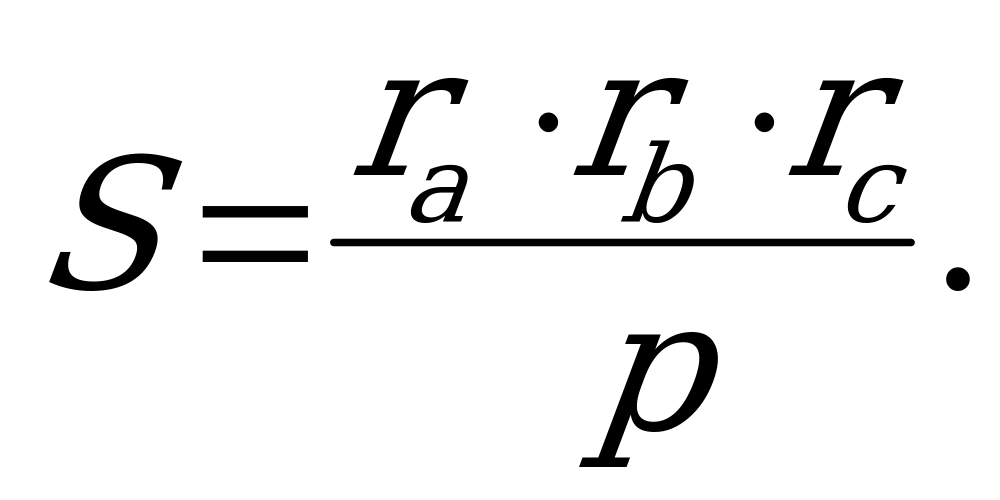 (7)
(7)


 6
6




 1,5
1,5






 C
C




 Прямоугольник
Прямоугольник















 В АС = 10см, АВ = 18см, ВМ = 6см.
В АС = 10см, АВ = 18см, ВМ = 6см. 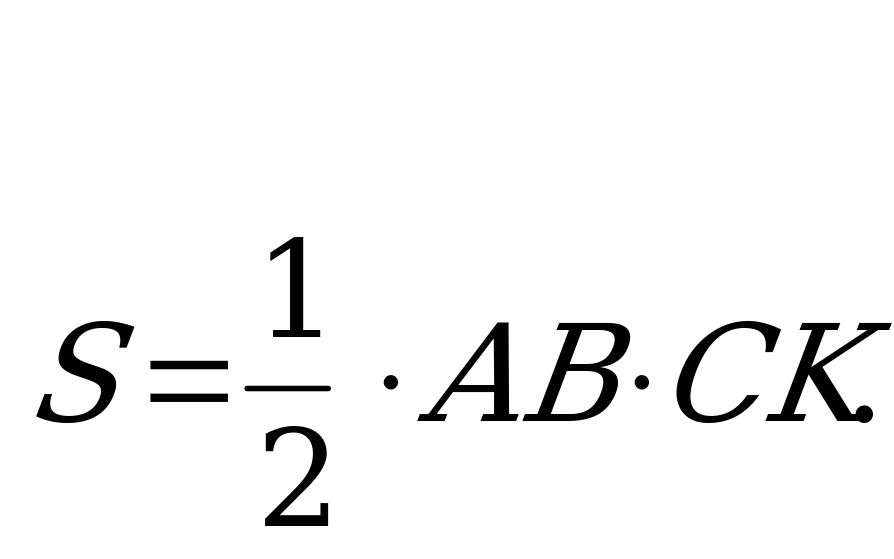 Но площадь можно найти по-другому:
Но площадь можно найти по-другому: ано: Решение.
ано: Решение. айти:
айти: 

 А
А
 Е
Е 
 А
А 

 O F О
O F О
 C G B C B G
C G B C B G
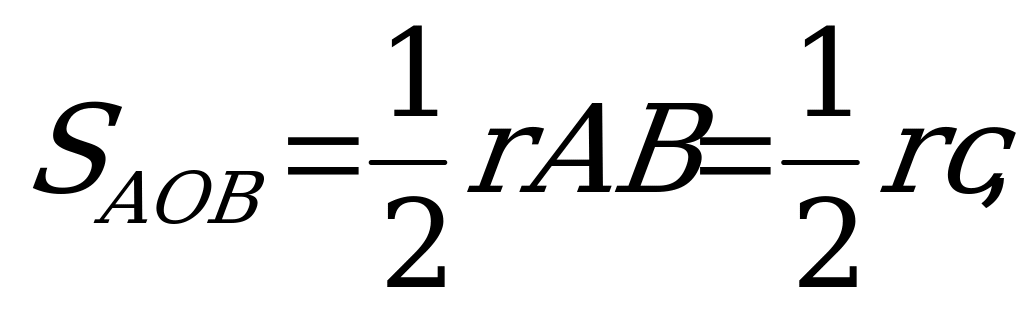


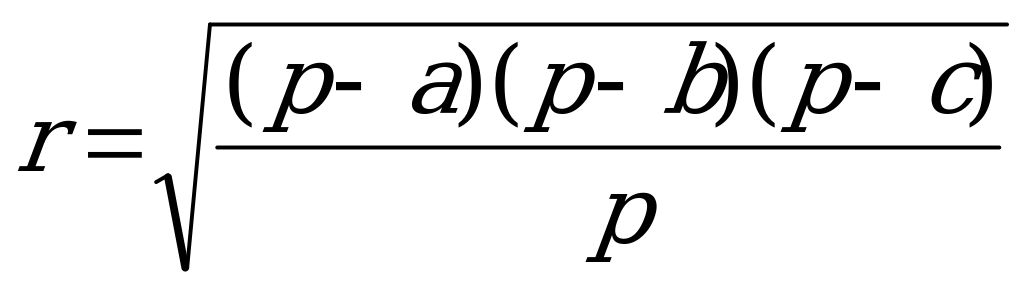 (1).
(1).
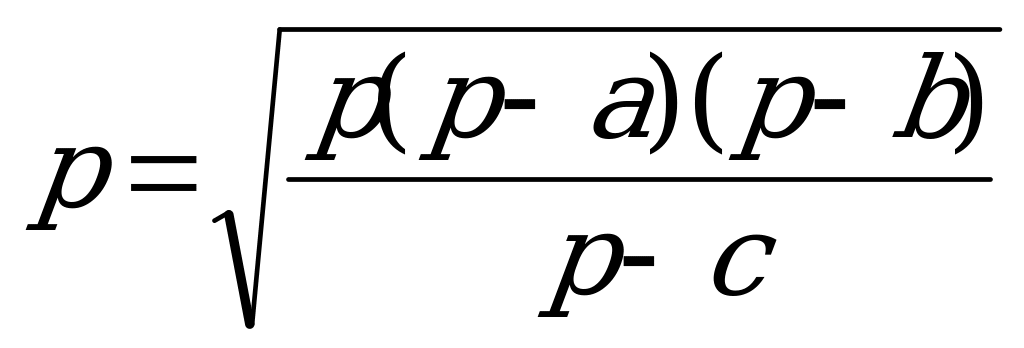 (2).
(2).

 окажем это.
окажем это.

 N
N SMOD + SBOM = SMBD; SBON + SBOM = SMBN, но (рис. 10)
SMOD + SBOM = SMBD; SBON + SBOM = SMBN, но (рис. 10)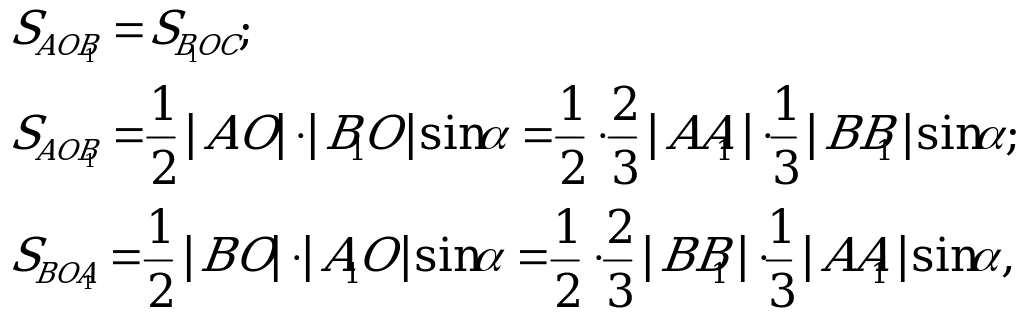


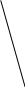 В следовательно,
В следовательно, 
 С1 а А1 ными сторонами можно найти по формуле Герона, а
С1 а А1 ными сторонами можно найти по формуле Герона, а

 А В1 С Стороны треугольника СОВ2 равны 6см, 8см и 10см.
А В1 С Стороны треугольника СОВ2 равны 6см, 8см и 10см.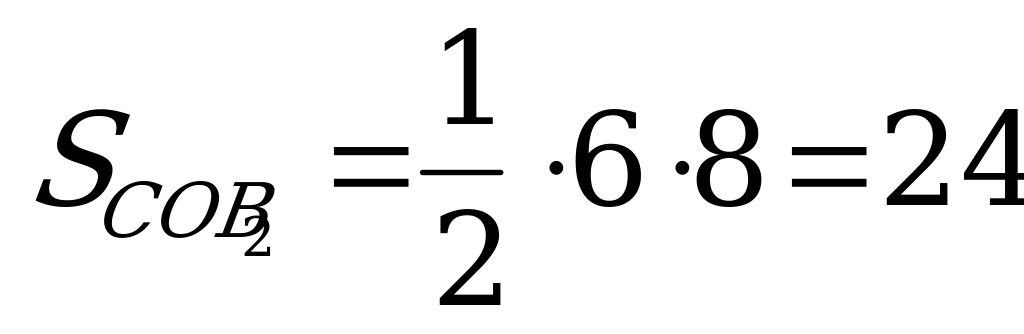 (см2), SABC = 72 (cм2).
(см2), SABC = 72 (cм2). ано:
ано: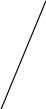
 АВС, B
АВС, B P||AB, P
P||AB, P OPK = S2, N S2
OPK = S2, N S2 LOF = S3. M S1 O K
LOF = S3. M S1 O K айти:
айти: A C
A C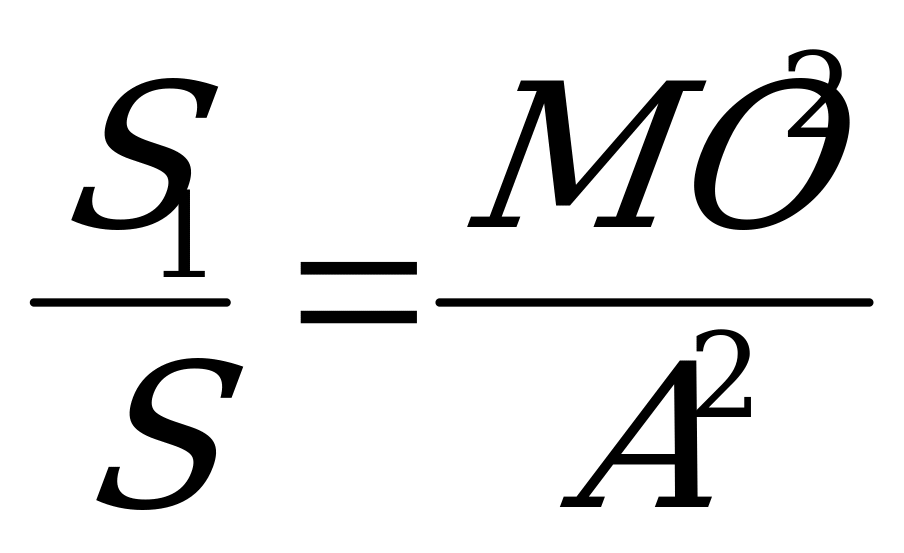 (площади подобных треугольников относятся как квадрат коэффициента подобия).
(площади подобных треугольников относятся как квадрат коэффициента подобия).