Реферат по математике "Пифагорейские числа"

Муниципальное бюджетное общеобразовательное учреждение

«Октябрьская средняя общеобразовательная школа №2»

Пифагорейские числа

Реферат по математике

Выполнила ученица 9 Б класса

Резанова Карина

Преподаватель –

Захарова Людмила Геннадьевна.

п. Октябрьский, 2018

Содержание

Введение………………………………………………………….………...................................3

Глава 1. Пифагор и пифагорейцы в истории математики…………………………………….4

Глава 2. Теория чисел и арифметика пифагорейцев…………………………………………5

2.1. Фигурные числа……………………………………………………………………………5

2.2 Пифагоровы тройки………………………………………………………………………...5

2.3 Совершенные и дружественные числа……………………………………………………6

2.4 Таблица Пифагора…………………………………………………………………………..7

Глава 3. Фигурные числа в современном мире……………………………………………….8

Заключение………………………………………………………………………………………9

Список использованных источников………………………………………………………….10

Приложение…………………………………………………………………………………….11

Введение

Актуальность темы моего реферата состоит в том, что числа очень важны в нашем мире. Без чисел нам было бы очень трудно и неинтересно жить. Хоть числа и произошли очень давно, их актуальность в современном мире приобретает все большее значение.

Все современные технологии связаны с цифрами и называются цифровыми, вся информация и даже музыка хранится в цифровом формате. Мне всегда хотелось узнать что-то новое. Ведь мир чисел очень загадочен и интересен. Мне захотелось узнать как можно больше о происхождении чисел, об их значении в нашей жизни. Думаю, что данная тема интересна не только мне.

Я стала собирать информацию. Каково же было мое удивление, когда я узнала, что учение о числах связано с Пифагором. Оказывается, что Пифагор и его ученики развивали не только геометрию, но и арифметику. Причем учение о числах у них тесно переплеталось с учением о геометрических фигурах. Так появилась тема реферата «Пифагорейские числа».

Пифагорейцы составляли из костяшек или камешков различные фигуры, изображали числа в виде точек, группируемых в геометрические фигуры. Такие числа получили в дальнейшем название фигурных чисел. Ими были введены дружественные и совершенные числа, составлены пифагоровы тройки. Пифагорейское происхождение имеет и таблица умножения. Обо всем этом я решила написать в своем реферате.

Для раскрытия темы реферата перед автором стоят следующие задачи:

1. описать, какой вклад в развитие математики внесли Пифагор и его ученики;

2. изучить и изложить информацию о появлении фигурных чисел, пифагоровых троек, совершенных и дружественных чисел, таблицы Пифагора;

3. найти примеры использования фигурных чисел в современном мире.

При написании реферата я использовала информацию из Интернета, искала на различных тематических сайтах исторические данные для раскрытия отдельных глав. Использовала материал из книги для раскрытия темы и составления содержания реферата. Труднее всего было найти информацию о «пифагоровых» числах в современном мире.

Глава 1. Пифагор и пифагорейцы в истории математики

Основоположником Пифагорейской школы был Пифагор, живший в 6 веке до н.э. Его учеников называли пифагорейцами, а саму школу Пифагорейской школой. Школа существовала в период с 585 до 400 г.г. до н.э.

Значительное внимание Пифагор и пифагорейцы уделяли развитию математики. Многие достижения, приписываемые Пифагору, на самом деле являются заслугой его учеников. Пифагорейцы занимались астрономией, геометрией, арифметикой (теорией чисел), создали теорию музыки.

Пифагорейцы полагали, что в основе всех законов природы лежит арифметика. Арифметика у них строилась не на аксиоматической базе. Свойства натуральных чисел считались самоочевидными, однако доказательства теорем и здесь проводили неуклонно.

Они изучали раздел геометрии, называемой планиметрией. Одна из основных теорем евклидовой геометрией является теорема Пифагора, устанавливающая соотношения между сторонами прямоугольного треугольника. В настоящее время известно, что эта теорема не была открыта Пифагором. Одни полагают, что Пифагор первым дал ее полноценное доказательство, а другие отказывают ему в этой заслуге. Теорема Пифагора издавна применялась в разных областях науки и техники, в практической жизни. Область применения теоремы достаточно обширна. Это было первое утверждение, связавшее длины сторон прямоугольного треугольника.

Так же пифагорейцам принадлежат открытия в теории делимости чисел. Ими были открыты «пифагоровы тройки», они научились выполнять с дробями сравнение, приведение к общему знаменателю и все четыре арифметических действия (сложение, вычитание, деление, умножение).

Можно справедливо утверждать, что Пифагор и пифагорейская школа закладывают основы теории чисел и принципы арифметики. Арифметическим путем пифагорейцы решают многие геометрические задачи того времени. Изучение зависимости между числами, и в частности между рядами чисел, требовало весьма развитого уровня абстрактного мышления, и этот факт отразился на философских взглядах Пифагора. Благодаря пифагорейцам числа были подняты на уровень реальной сущности всех вещей.

Глава 2. Теория чисел и арифметика пифагорейцев

2.1. Фигурные числа

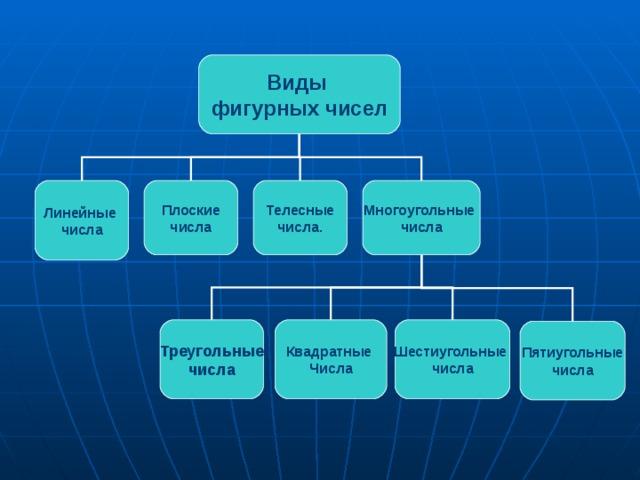
«Числа правят миром» - такой тезис выдвинул когда-то Пифагор. Он считал, что главная наука о числе, арифметика, неразрывно связана с геометрией, а числа можно изображать, выкладывая камешками, в форме геометрических фигур. Такие числа они называли фигурными. Все числа они делили на линейные, плоские, телесные, треугольные, квадратные, пятиугольные.

 Линейными числами называли числа, которые, которые делятся только на единицу и на самих себя (например, число 5) и могут быть изображены в виде линии, составленной из последовательно расположенных точек.

 К плоским числам они относили числа, которые могли быть изображены и представлены в виде произведения двух сомножителей (например, число 6).

Телесные числа - это числа, которые могут быть выражены произведением трех сомножителей.

Числа, которые могли быть изображены треугольниками, называли треугольными (3, 6, 9), а числа, изображающие квадраты - квадратными (4,16), изображающие пятиугольники - пятиугольные числа (5, 12, 22).

Представление чисел в виде правильных геометрических фигур помогало пифагорейцам находить различные числовые закономерности, открывать законы арифметических операций, а также легко переходить к числовой характеристике геометрических объектов - измерениям площадей и объемов.

Именно от фигурных чисел пошло выражение "Возвести число в квадрат или куб".

2.2 Пифагоровы тройки

Задача, которую в современных терминах можно сформулировать так: решить в натуральных числах неопределенное уравнение x²+y²=z², является задачей Пифагора.

Это уравнение с тремя неизвестными называют уравнением Пифагора потому, что в первый раз его обнаружили в трудах Пифагора, а только потом историки нашли более ранние подтверждения того, что его знали и в Древнем Египте и Древнем Вавилоне.

Набор из трёх натуральных чисел (x,y,z), удовлетворяющих уравнению, будет являться его решением. Такие решения называют пифагоровыми тройками. Например, (3, 4, 5) является пифагоровой тройкой. Пифагорейцы изобрели метод отыскания таких троек и, доказали, что пифагоровых троек существует бесконечно много. Однако, общего решения такого уравнения не найдено до сих пор.

Если умножить найденные решения x,y, z  на одно и то же натуральное число, то получится другая пифагорова тройка. Например: (3, 4, 5), (6, 8, 10), (9, 12, 15), (12, 16, 20). Среди пифагоровых троек есть и такие: (5, 12, 13) (8, 15, 17) (7, 24, 25). Они не могут быть получены предложенным способом. В этих тройках числа являются взаимно простыми, их общий делитель равен единице. Это простейшие (примитивные) тройки.

Пифагоровы тройки используются в геометрии. Треугольник, стороны которого равны пифагоровым числам, является прямоугольным.

Этим свойством пользовались еще древние египтяне для построения прямых углов при планировке земельных участков и сооружений зданий. На веревке отмерялись последовательно 3 отрезка длиной в 3, 4 и 5 единиц длины. Если соединить концы этой веревки и натянуть ее на 3-м и 7-м делении, то получится прямоугольный треугольник. Прямоугольный треугольник, с катетами 3, 4 и гипотенузой 5 называется египетским треугольником.

2.3 Совершенные и дружественные числа

Пифагор и его ученики изучали вопрос о делимости чисел.

Число равное сумме всех его делителей (без самого числа) они называли совершенным числом. Например, числа 6 (6=1+2+3), 28 (28=1+2+4+7+14) совершенные. Следующие совершенные числа 496, 8128, 33550386. Пифагорейцы знали только первые три совершенных числа 6,28, 496.

  Совершенных чисел немного. Все они четны и являются простыми числами. Однако вопрос о том, имеется ли конечное или бесконечное число совершенных чисел, до сих пор не решен, также не найдено ни одного нечетного совершенного числа и не доказано, что таких чисел не существует.

Когда Пифагора спросили о том, кого считать своим другом, он ответил: «Того, кто является моим вторым Я, как числа 220 и 284. Эти два числа замечательны тем, что сумма делителей каждого из них равна второму числу».

  Делители для 220 это: 1; 24; 5; 10; 11; 20; 22; 44; 55 и 110, сумма делителей равна 284. Делители для 284 это: 1; 2; 4; 71 и 142.

Сумма делителей числа 220 - это 1+2+4+5+10+11+20+22+44+55+110=284, а сумма делителей числа 284 - это 1+2+4+71+142=220.

2.4 Таблица Пифагора

Еще одним изобретением великого греческого ученого стала таблица Пифагора. Сейчас ее принято называть таблицей умножения, по которой в те годы обучались ученики школы философа.

Первое изображение таблицы умножения в виде квадрата 10x10 приведено в книге «Введение в арифметику» Никомаха Геразского (I-II век). Автор отмечал, что такое изображение таблицы умножения  применял Пифагор. Цифры таблицы Пифагора были записаны в ионийской нумерации, использующей 24 буквы греческого алфавита и 3 архаические буквы финикийцев (6=вау,  90=коппа,  900=сампи). Чтобы отличить цифры от букв, над числами рисовали горизонтальную черту – титло.

Таблица Пифагора представляет собой таблицу, по горизонтали и вертикали которой расположены числа натурального ряда, а на пересечении столбцов и строк стоят их произведения. Диагональ таблицы образует квадраты чисел. Таблицу Пифагора можно расширять вправо и вниз до бесконечности, соблюдая единственное условие: каждое число таблицы есть произведение номера строки и номера столбца.

Пифагор гордился своей таблицей умножения, называя ее своим высшим достижением.

Глава 3. Фигурные числа в современном мире

Мы не задумываемся о том, что ежедневно встречаемся с фигурными числами. А ведь это так просто и интересно.

При изучении формулы площади прямоугольника используется понятие плоского числа, которое представляется виде произведения двух сомножителей – длины и ширины.

При вычислении объёма прямоугольного параллелепипеда применяется понятие телесного числа, выражаемого произведением трёх сомножителей – длины, ширины и высоты.

Упаковка конфет в форме линейного числа.

На параде солдаты стоят правильными рядами, образуя квадраты или прямоугольники (плоские числа).

Во время различных праздников мы видим показательные выступления лётчиков. Самолёты в воздухе образуют треугольные или другие фигурные числа.

Треугольные числа можно встретить в самых обычных местах.

Фигурные числа встречаются при упаковке различных товаров в коробки и другие ёмкости.

Телесные числа используются при упаковке конфет, консервных банок, блокнотов, тетрадей, ручек и др. в различные ёмкости.

Плоские числа тоже часто используются при упаковке конфет, растительного масла, лимонадных бутылок.

К фигурным числам можно отнести пирамидальные числа, которые получаются, если шарики складывать пирамидкой. Как раньше складывались ядра около пушки.

Заключение

Математика, как теория, получила развитие в школе Пифагора в период с 585 до 400 г.г. до н.э. Главной заслугой пифагорейцев в области науки является существенное развитие математики, как по содержанию, так и по форме. По содержанию – открытие новых математических фактов. По форме - построение арифметики и геометрии как теоретических, доказательных наук, изучающих свойства отвлеченных понятий о числах и геометрических формах.

Пифагорейцы называли собственные исследования «математа», что означает «науки» и делили их на 4 части: арифметику, геометрию, астрономию, гармонию (учение о музыке). Главной считалась арифметика – наука о числах. Именно она лежала в основе и геометрии, и астрономии, и гармонии.

В процессе работы над своим рефератом, я узнала много нового. Раньше я не интересовалась данной темой. Сейчас, когда я изучила, как возникли фигурные числа, пифагоровы тройки, совершенные и дружественные числа, узнала, что таблица умножения является таблицей Пифагора, я поняла, что изучать историю математики необходимо. Так много интересного можно о ней узнать.

Таким образом, вклад Пифагора и его учеников в развитии  науки математики бесценен.

 В целом, можно сказать, что все задачи, которые были поставлены во введении, выполнены.

 

Список использованных источников

1. Волошинов, А.В. Пифагор: союз истины. добра и красоты /А.В. Волошинов. — 1993: Просвещение, 224с.

2. Энциклопедический словарь юного математика /А.П.Савин. — 1989: Педагогика, 352с.

3. Пифагор и греческая математика [Электронный ресурс] /- [сайт].- URL: /.: http://referatwork.ru/(дата обращения: 2.12.18)

4. Пифагорейская математика [Электронный ресурс] /- [сайт].- URL: /:http://www.symbolizm.ru/(дата обращения: 2.12.18)

5. Классика греческой науки (пифагорейская школа) [Электронный ресурс] /- [сайт].- URL: /: https://studbooks.net/(дата обращения: 2.12.18)

6. Доказательство [Электронный ресурс] /- [сайт].- URL: /. https://studopedia.ru/(дата обращения: 5.12.18)

Приложение

Пирамидальные числа

Телесные числа

Плоские числа

Линейные числа