Решение планиметрических задач (прототип ОГЭ №24, 25)

Решение планиметрических задач (прототип заданий ОГЭ № 24, 25)»

Выполнил: учитель математики МБОУ «Северная СОШ №2» Фонакова И.И.

Как решать задачи по геометрии:

• 1. Сделать рисунок по условию задачи
• 2. Отметить на рисунке все, что дано и что нужно найти
• 3. Записать все формулы и соотношения, которые приходят на ум
• 4. Составить уравнение и получить ответ

Типы задач

• 1. Задачи базового уровня – задачи требующие базовых знаний основных теорем.
• 2. Задачи повышенного уровня сложности – двух-трех ходовая задача, для решения которой нужно достаточно свободно ориентироваться в материале школьного курса планиметрии.
• 3. Задачи на доказательства – это задачи в которых требуется подтвердить или опровергнуть утверждение из условия задачи.

Связь между задачами первой и второй части

Задача повышенного уровня сложности №24

• Это планиметрическая задача на вычисление, для решения которой нужно достаточно свободно ориентироваться в материале школьного курса планиметрии, в его теоремах, связанных с треугольниками, многоугольниками (преимущественно параллелограммами и трапециями) и окружностями

Критерии оценивания 24 задачи

Типичные ошибки

• Неправильно выполнен рисунок
• Использование данных, которых нет в условии
• Нет ссылок на используемые теоремы и свойства.

Задача №24

В

1 способ:

О

С

А

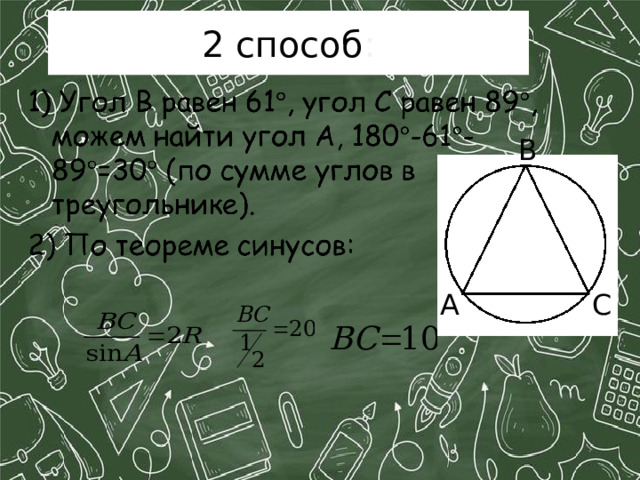
2 способ :

В

А

С

• В данной задаче были использованы теоремы о сумме углов в треугольнике, свойства равнобедренного треугольника, свойства вписанных и центральных углов. Т.е несколько шагов пришлось выполнить и связать между собой в одной задаче. А в задачах первой части, используются такие же теоремы, только в каждой задаче по одной.

Например задача № 16 этого же варианта

Задача № 17

• Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен 60°. Найдите радиус окружности.
• Здесь, как и в 24 задаче применяется свойства равнобедренного треугольника и знание окружности и ее элементов.

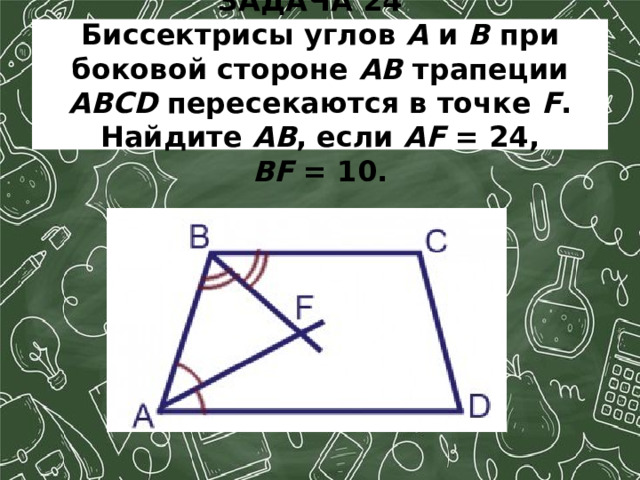
ЗАДАЧА 24 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F . Найдите AB , если AF  = 24, BF  = 10.

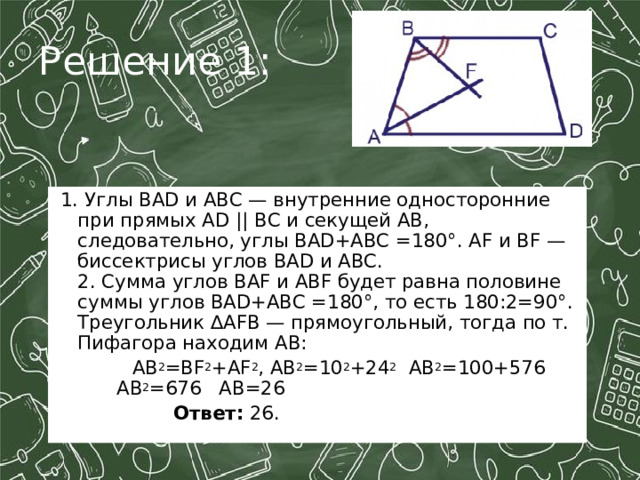
Решение 1:

1. Углы BAD и ABC — внутренние односторонние при прямых AD || BC и секущей AB, следовательно, углы BAD+ABC =180°. AF и BF — биссектрисы углов BAD и ABC. 2. Сумма углов BAF и ABF будет равна половине суммы углов BAD+ABC =180°, то есть 180:2=90°. Треугольник ∆AFB — прямоугольный, тогда по т. Пифагора находим AB:

AB 2 =BF 2 +AF 2 , AB 2 =10 2 +24 2 AB 2 =100+576 AB 2 =676 AB=26

Ответ:  26.

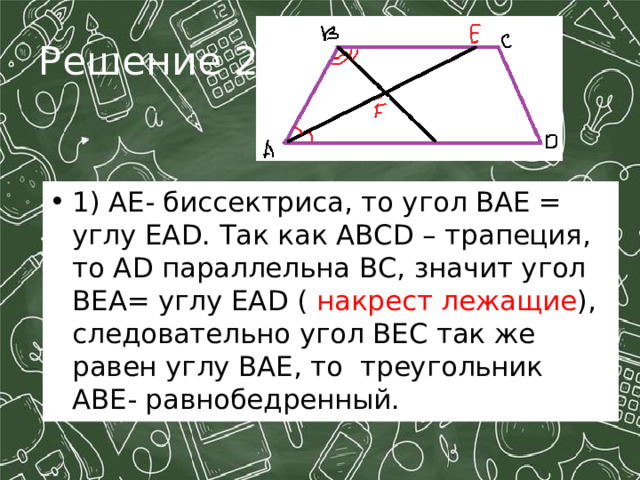
Решение 2:

• 1) АЕ- биссектриса, то угол ВАЕ = углу ЕА D . Так как ABCD – трапеция, то А D параллельна ВС, значит угол ВЕА= углу ЕА D ( накрест лежащие ), следовательно угол ВЕС так же равен углу ВАЕ, то треугольник АВЕ- равнобедренный.

• 2) Рассмотрим АВЕ- равнобедренный (см.1 ) , В F - биссектриса (по условию) и высота ( по свойству равнобедренного треугольника ), значит угол AFB =90.

3) Треугольник AFB — прямоугольный, тогда по т. Пифагора находим AB:

• AB 2 =BF 2 +AF 2 , AB 2 =10 2 +24 2 AB 2 =100+576 AB 2 =676 AB=26

В данной задаче были использованы свойства равнобедренного треугольника, признаки параллельности прямых и теорема Пифагора. Т.е снова нужно связать между собой знание базовых теорем. В первой части они так же применяются.

Задача № 16

• Найдите величину острого угла параллелограмма , если биссектриса угла образует со стороной угол, равный 31°. Ответ дайте в градусах.
• Здесь нужно применить , как и в 24 задаче знание накрест лежащих углов, т.е признаков параллельности прямых и свойство биссектрисы угла.

Задача №25

• Это планиметрическая задача на доказательство, связанная со свойствами треугольников, четырехугольников, окружностей.

Типичные ошибки:

• Неправильно выполнен рисунок
• Использование данных, которых нет в условии
• Нет ссылок на используемые теоремы и свойства.

Что нужно помнить при решении 25 задачи:

• 1) Треугольники и их элементы:

признаки равенства треугольников; признаки подобия треугольников; свойства сторон и углов треугольника; площадь; свойства медианы; биссектрисы и высоты треугольника; средняя линия и серединный перпендикуляр треугольника; равнобедренный, равносторонний и прямоугольный треугольники; окружность, описанная около треугольника и вписанная в треугольник

• 2) Окружности и их элементы:

понятие окружности, круга и их элементов; взаимное расположение прямой и окружности; свойства хорд окружности; касательные и секущие к окружности; свойства углов в окружности; свойства вписанных углов; взаимное расположение двух окружностей; общие касательные двух окружностей.

• 3) Четырехугольники и их элементы:

виды четырехугольников и их свойства; вписанные и описанные четырехугольники; правильные многоугольники.

Треугольники и их элементы. Окружность и ее элементы. Задача №25.

В окружности с центром О проведены две хорды АВ и CD так, что центральные углы АОВ и СОD равны. На эти хорды опущены перпендикуляры ОК и OL . Докажите, что ОК и OL равны.  

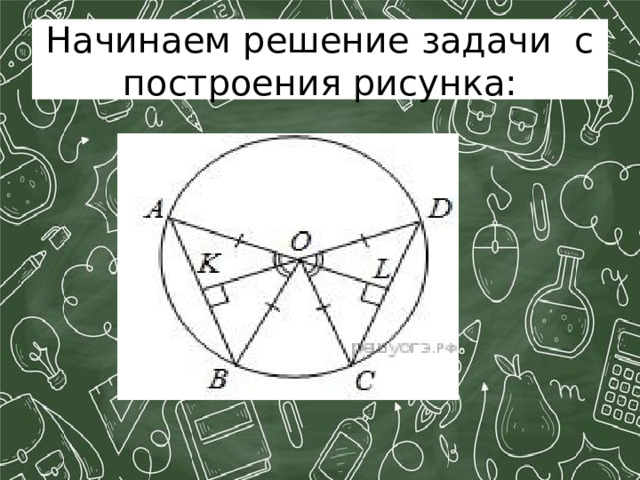
Начинаем решение задачи с построения рисунка:

Доказательство:

Треугольники  АОВ  и  СОD  равны по двум сторонам и углу между ними ( AO = BO = CO = DO  как ра­ди­у­сы окружности, ∠ AOB  = ∠ COD  по условию). Следовательно, высоты  OK  и  OL  равны как соответственные элементы равных треугольников.

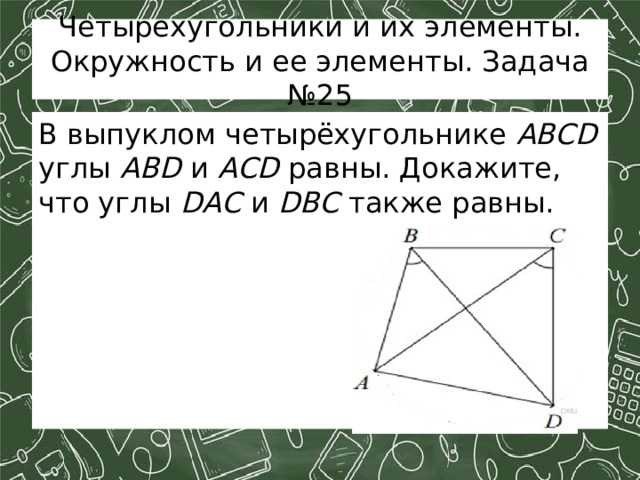
Четырехугольники и их элементы. Окружность и ее элементы. Задача №25

В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.  

Доказательство:

1) ∠АB D и ∠ ACD опираются на отрезок

A D и равны друг другу.

Значит мы можем провести окружность

через точки A D и вершины этих углов.

Эти углы окажутся вписанными в окружность, опирающимися на одну дугу. Получится, что мы описали окружность вокруг четырехугольника.

2) Заметим, что углы DAC и DBC тоже являются вписанными и опирающимися на одну и ту же дугу, т.е., используя теорему о вписанном угле, получаем, что они равны друг другу . ч.т.д.

Окружность и ее элементы. Треугольники и их элементы. Четырехугольники и их элементы Задача №25

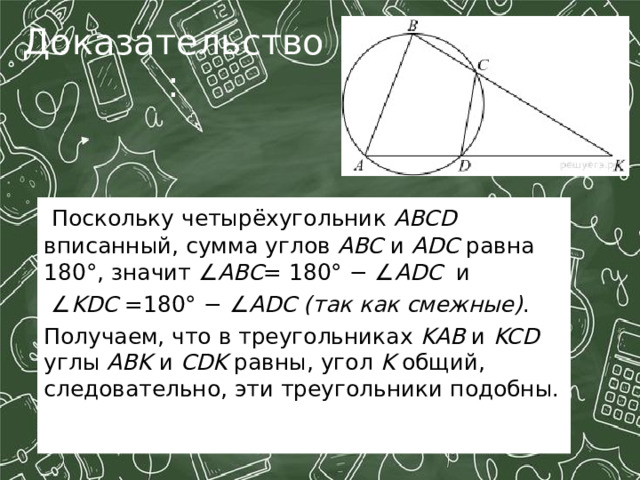
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD  и  BC четырёхугольника пересекаются в точке K . Докажите, что треугольники KAB и KCD подобны.

Начинаем с построения рисунка:

Доказательство:

Поскольку четырёхугольник ABCD вписанный, сумма углов ABC и ADC равна 180°, значит ∠ ABC = 180° − ∠ ADC и

∠ KDC =180° − ∠ ADC (так как смежные) .

Получаем, что в треугольниках KAB и KCD углы ABK и CDK равны, угол K общий, следовательно, эти треугольники подобны.

Спасибо за внимание!!!