Решение текстовых задач .Математика. 11 класс.

Решение текстовых задач

11 класс

учитель математики

первой категории

МАОУ № 61

Ветошника Вера Александровна

г. Нижний Тагил

Основные сведения

При решении текстовых задач на смеси и сплавы постоянно приходится работать со следующими понятиями.

Абсолютное содержание вещества в смеси – это количество вещества, выраженное в обычных единицах измерения (граммах, литрах и т.д.).

Относительное содержание вещества в смеси – это отношение абсолютного содержания к общей массе (объему) смеси, т.е.

абсолютное содержание

Относительное содержание =

общая масса

Часто относительное содержание называют концентрацией или процентным содержанием, а абсолютное содержание - количество чистого вещества.

Задачи на смеси и сплавы охватывают большой круг ситуаций:

• смешение товаров разной цены;
• смешение жидкостей с различным содержанием соли;
• смешение кислот разной концентрации;
• сплавление металлов с разным содержанием некоторого металла.

Смешали a литров процентного раствора вещества с b литрам n и m - процентного водного раствора этого вещества ( растворы ,можно заменить сплавами)

• 0,01· a ·n = 0,01an ( литров) в первом растворе
• 0,01· b ·n = 0,01bm ( литров) во втором растворе
• 0,01an + 0,01bm ( литров) количество чистого вещества в смеси.
• Всего этой смеси пол (a+ b ) литров
• Тогда искомая концентрация

k= (an + bm)

(0,01an + 0,01bm)100

k=

a +b

a +b

Самостоятельная работа .

1)В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

2) Первый сплав содержит 5% меди, второй -11% меди. Масса второго сплава больше массы первого на 4кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава . Ответ дайте в килограммах?

Решение задачи № 1

• В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора? Концентрация раствора равна С =
•  
• Объем вещества в исходном растворе равен 0,12 · 5 =0,6  литра . При добавлении 7 литров воды общий объем раствора увеличится, а объем растворенного вещества останется прежним. Таким образом,
• 0, 6 : (5+7 ) · 100% = 5 % концентрация полученного раствора равна:
• Ответ: 5.

Примечание.

• В текстовых задачах по математике предполагается, что объем раствора, образованного при сливании двух жидкостей, равен сумме их объемов. Это такая же условность, как «мгновенный разворот» в задачах на движение. В действительности, объем (в отличие от массы) не обладает таким свойством.

V вещества

· 100%

V раствора

Решение задачи №2

Первый сплав содержит 5% меди, второй -11% меди. Масса второго сплава больше массы первого на 4кг.

Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава . Ответ дайте в килограммах?

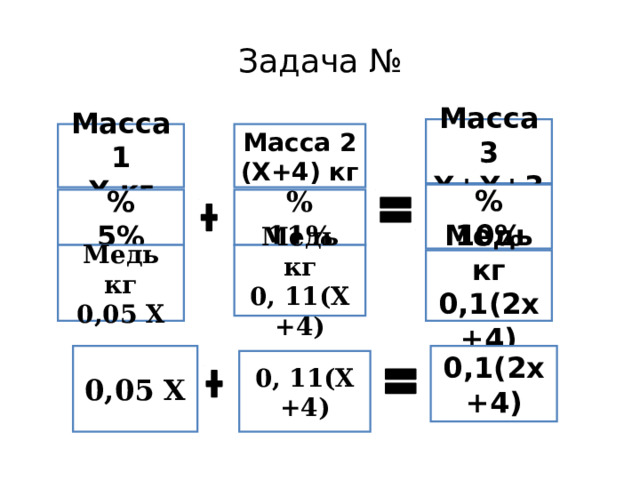
Задача №

Масса3

Х+Х+3

Масса 1

Х кг

Масса 2

(Х+4) кг

%

10%

%

11%

%

5%

Медь кг

0, 11(Х +4)

Медь кг

0,05 Х

Медь кг

0,1(2х+4)

0,05 Х

0,1(2х+4)

0, 11(Х +4)

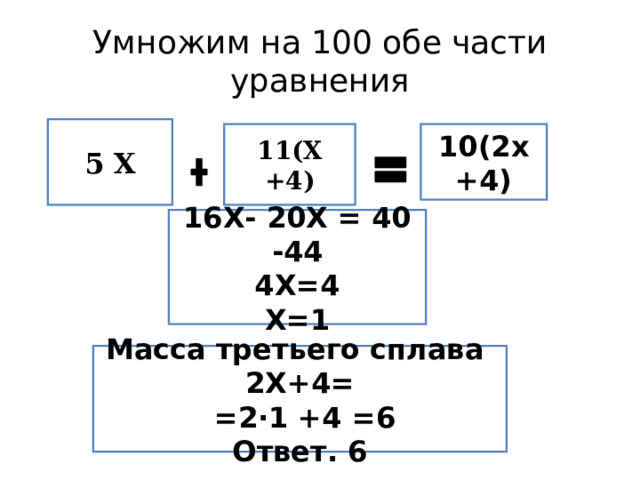
Умножим на 100 обе части уравнения

5 Х

11(Х +4)

10(2х+4)

16Х- 20Х = 40 -44

4Х=4

Х=1

Масса третьего сплава 2Х+4=

=2·1 +4 =6

Ответ. 6

Задача № 3

В сосуд, содержащий 10 литров

24-процентного водного раствора некоторого вещества , добавили 5 литров воды. Сколько процентов составит концентрация получившегося раствора?

Задача № 3

В сосуд, содержащий 10 литров

24-процентного водного раствора некоторого вещества , добавили 5 литров воды. Сколько процентов составит концентрация получившегося раствора?

Концентрация раствора равна С =

Объем вещества в исходном растворе равен 0,24 · 10 =2,4   литра . При добавлении 5 литров воды общий объем раствора увеличится, а объем растворенного вещества останется прежним. Таким образом,

2, 4 : (10 + 5 ) ·100% = 16 % концентрация полученного раствора равна:

Ответ: 16.

V вещества

· 100%

V раствора

Алгоритм1. Арифметический способ решения

При образовании смеси складываются абсолютные содержания. Поэтому, если известны только относительные содержания, то нужно:

• подсчитать абсолютные содержания компонентов каждой смеси;
• сложить абсолютные содержания, то есть подсчитать абсолютные содержания компонентов полученной смеси;
• найти массу полученной смеси;
• подсчитать относительное содержание компонентов полученной смеси.
• Записать ответ.

• Смешали некоторое количество 15 –процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
• 0,15 Х + 0,19 Х = 2· Х · 0 ,0 1·k
• 0,34Х=0,02Х k
• K= 17

Х+Х кг

Х кг

Хкг

K%

15%

19%

2· Х · 0 ,0 1·k

0,15 Х

0,19 Х

Задача 4. Даны два куска с различным содержанием олова. Первый, массой 300г, содержит 20% олова. Второй, массой 200г, содержит 40% олова. Сколько процентов олова будет содержать сплав, полученный из этих кусков?

Решение.

k = (300 • 0 ,2+200 • 0,4) • 100% : (300+200) =

300+200 г

300г

200г

= 28 %

K%

40% олова

20% олова

500 ·0,01 k

Ответ: 28

200·0,4

300 ·0,2

Задача 4. Даны два куска с различным содержанием олова. Первый, массой 300г, содержит 20% олова. Второй, массой 200г, содержит 40% олова. Сколько процентов олова будет содержать сплав, полученный из этих кусков?

300г

Решение.

• 300 •20 : 100 = 60 (г) - олова в первом сплаве, 200 • 40 : 100 = 80 (г) - олова во втором сплаве ;
• 60 + 80 = 140 (г) - олова в двух сплавах вместе;
• 200 + 300 = 500 (г) – масса куска после сплавления;
• 140 : 500 • 100 = 28% -содержится олова после сплавления.

Или k = (300 • 0 ,2+200 • 0,4) • 100% : (300+200) =

20% олова

200г

= 28 %

40% олова

Ответ: 28

Алгоритм2. Применение линейного уравнения

При составлении уравнения прослеживается содержание какого-нибудь одного вещества из тех, которые сплавляются (смешиваются) и т.д.

• Обозначить неизвестную величину через х.
• Составить уравнение по условию задачи.
• Решить получившееся уравнение.
• Перейти к условию задачи (ответить на вопрос).
• Записать ответ.

Задача № 5 . Сколько литров воды надо добавить к 20 литрам 5% раствора соли, чтобы получить 4% раствор?

Решение.

Пусть количество добавленной воды – х (л),

тогда масса нового раствора – 20+х (л),

20×0,05=1(л)- содержится соли в 20 литрах 5% раствора.

Имеем : соли 1 (л) это 4%,

раствора 20+х (л) это 100%.

Составим и решим уравнение:

1 : (20 +х)= 4 :100

0,8 + 0,04 Х = 1

0,04 Х = 0, 2

Х = 5

20 (л)

5% соли

Ответ. 5

Алгоритм 3. Применение систем линейных уравнений

• Обозначить одну неизвестную величину через х, другую неизвестную величину через у.
• Составить систему двух линейных уравнений по условию задачи.
• Решить получившуюся систему уравнений.
• Перейти к условию задачи (ответить на вопрос).
• Записать ответ.

Задача 6 . Имеется два раствора поваренной соли разной концентрации. Если слить вместе 100г первого раствора и 200 г второго раствора, то получится 50%-й раствор. Если же слить вместе 300г первого раствора и 200г второго, то получится 42%-й раствор. Найти концентрацию второго раствора.

Решение.

Пусть процентное содержание соли

в первом растворе – х %,

а во втором растворе – у %.

Составим и решим систему уравнений:

х + 2у = 0,5·(100+200),

3х + 2у = 0,42(300+200);

х + 2у = 150,

3х + 2у = 210;

х = 30,

у = 60.

100 (г)

200 (г )

Ответ: 60% концентрация второго раствора.

Задача№7 Первый сплав содержит 20% меди, второй -80% меди. Масса первого сплава больше массы второго на 60 кг. Из этих двух сплавов получили третий сплав, содержащий 32% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Масса 1 сплава

Х + 60 кг

Масса 2 сплава

Х кг

Масса 3 сплава

2Х +60 кг

• х кг

20%

80%

32%

0,2 (Х+60)

0,8 Х

0,32(2Х+60)

• 0,2 Х+12+ 0,8Х = 0,64 Х +19,2
• 1Х- 0,64Х=19,2-12
• 0,36Х =7,2
• Х=720:36
• Х=20
• 2 · 20+60=100
• Ответ. 100

Задача № 8

Имеются два сосуда, содержащих 42 кг и 6 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор , содержащий 40% кислоты. Если же смешать равные массы этих растворов, то получится раствор ,содержащий 50% кислоты. Сколько килограммов кислоты содержится в первом растворе?

Задача № 8

Масса3

42+6

Масса 2

6 кг

Масса 1

42 кг

%

40%

%

У%

%

Х%

Медь кг

6У:100

кг

42Х : 100

Медь кг

48 ·40 :100

0,42 Х

0,4 ·48

0, 06 У

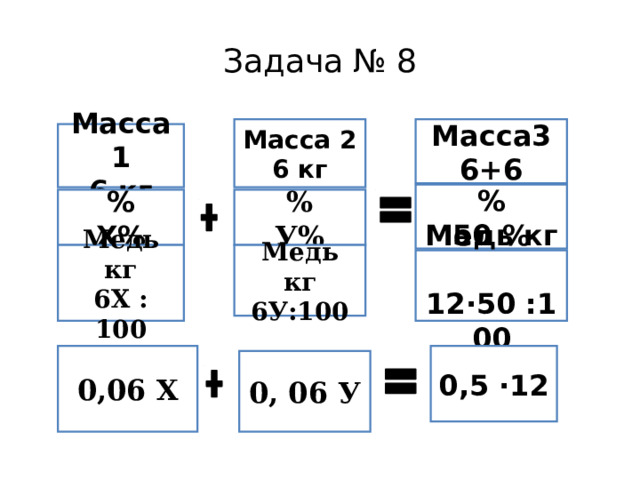
Задача № 8

Масса3

6+6

Масса 2

6 кг

Масса 1

6 кг

%

50 %

%

У%

%

Х%

Медь кг

6У:100

Медь кг

6Х : 100

Медь кг

12·50 :100

0,06 Х

0,5 ·12

0, 06 У

Составим систему уравнений

0,42 Х+0,06 У =0,4 · 48 Х= 110 : 3

0,06 Х+0,06 У =0,5 · 12 1) 0,42 · 110:3 =

42 Х + 6 У = 4 0 · 48 =15, 4 кг в

6 Х + 6 У = 5 0 · 12 первом растворе

36 Х + 0 = 10 · 12 ( 16 – 5) 1+2

36 Х = 120 · 11 12 · 11 = 1 3 2

36 Х = 1320

Х= 1320 :36 О твет. 15,4

Задача № 9

Смешали 14 литров 30 процентного водного раствора некоторого вещества с 10 литрами 18 процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора? Знак % в ответе не пишите.

1 способ .

C= (14·0,3+10·0,18):(14+10)·100%=

= 6:24·100% =25 % . Ответ. 25

Решение задачи № 9 2 способ .

• В 14 л - 30% процентного раствора содержится 0,3∙14= 4,2 л
• В 10л -18% процентного раствора этого же вещества 0,18 ∙ 10= 1,8 л
• Всего 14+10=24 литра смеси, что составляет 100% .
• В нем 4,2+1,8 =6 л- это всего вещества, что составляет х%. 24: 6 = 100 :Х
• Х = 25 Ответ. 25

Смешали 300г 50%-го и 100г 30%-го раствора кислоты. Определите процентное содержание кислоты в полученной смеси.

Решение. 1 способ.

Можно решить по формуле концентрации

С =( 300 · 0,5 + 100·0,3): (300+100) · 100% = 45%.

Смешали 300г 50%-го и 100г 30%-го раствора кислоты. Определите процентное содержание кислоты в полученной смеси.

Решение. 2 способ.

• В 300г - 50% процентного раствора содержится 0,5∙300 = 150 г
• В 100 г -30% процентного раствора этого же вещества 0,3 ∙ 100 = 30 г
• Всего 300+100= 400 г смеси, что составляет 100%
• В нем 150+30 =180 г - это всего вещества.
• 180 : 400 ·100% = 0,45· 100% = 45%
• Ответ. 45.

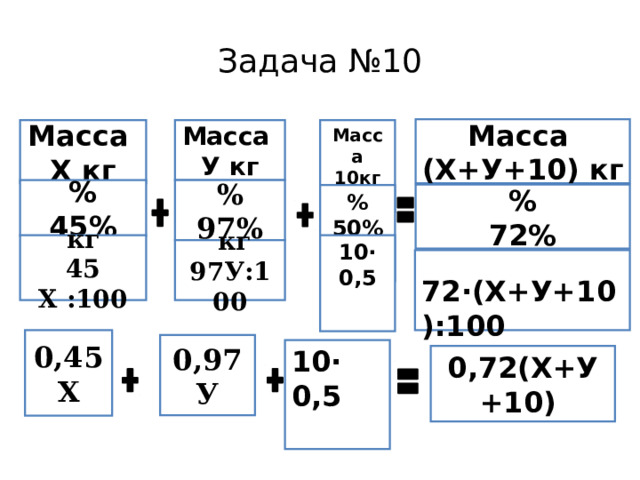
Задача №10

Смешали 45 %-й и 97%-й раствора кислоты и добавив 10 кг чистой воды, получили 62%-й раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50%-го раствора той же кислоты , то получили бы 77%-й раствор кислоты. Сколько килограммов 45 %- го раствора использовали для получения смеси?

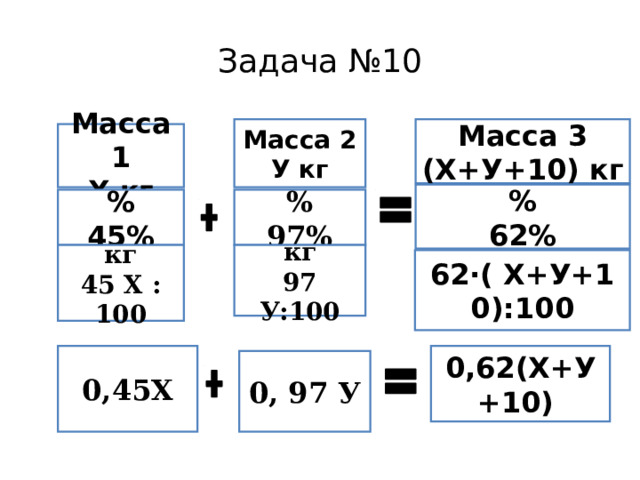
Задача №10

Масса 3

(Х+У+10) кг

Масса 2

У кг

Масса 1

Х кг

%

62%

%

97%

%

45%

кг

97 У:100

кг

45 Х : 100

62·( Х+У+10):100

0,45Х

0,62(Х+У+10)

0, 97 У

Задача №10

Масса

(Х+У+10) кг

Масса 10кг

Масса

Х кг

Масса

У кг

%

45%

%

97%

%

72%

%

50%

кг

45 Х :100

10∙ 0,5

кг

97У:100

72·(Х+У+10):100

0,45Х

0,97 У

10∙ 0,5

0,72(Х+У+10)

Составим систему уравнений

0,45Х + 0,97У = 0,62( Х+У+10) 52Х = 1300

0,45Х+ 0,97У+5=0,72( Х+У+10) х=25

45Х+97У=62 ( Х+У+10) Ответ.25

45Х+97У+ 500 = 72 ( Х+У+10)

-500 = -10( Х+У+10)

50 -10 = Х + У / ∙ 17

45Х+97У= 62Х+62У+620

+ 680 =17 Х+ 17 У

620 = -17Х+ 35У

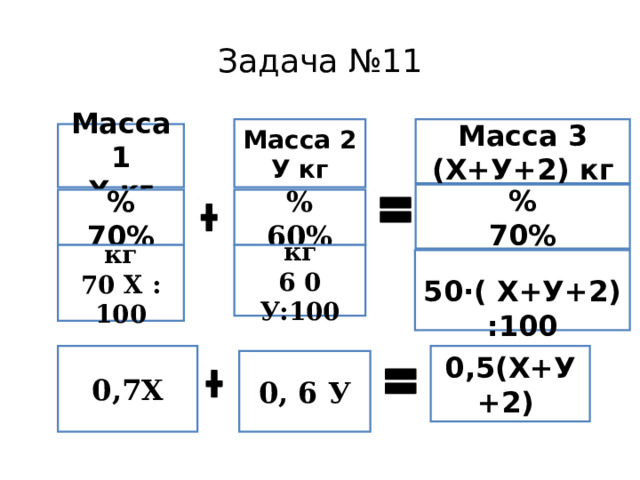
Задача №11

Смешали70%-й и 60%-й раствора кислоты и добавив 2 кг чистой воды, получили 50%-й раствор кислоты. Если бы вместо 2 кг воды добавили 2 кг 90%-го раствора той же кислоты , то получили бы 70%-й раствор кислоты. Сколько килограммов 70%- го раствора использовали для получения смеси?

Задача №11

Масса 3

(Х+У+2) кг

Масса 2

У кг

Масса 1

Х кг

%

70%

%

60%

%

70%

кг

6 0 У:100

кг

70 Х : 100

50·( Х+У+2):100

0,7Х

0,5(Х+У+2)

0, 6 У

Задача №11

Масса

(Х+У+2) кг

Масса 2кг

Масса

Х кг

Масса

У кг

%

70%

%

60%

%

50%

%

90%

кг

70 Х :100

2 ∙ 0,9

кг

6 0У:100

70·( Х+У+2) :100

0,7Х

0, 6 У

2 ∙ 0,9

0,7(Х+У+2)

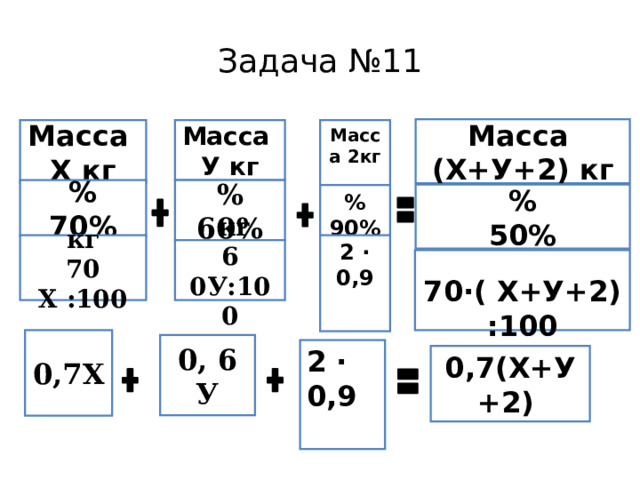
Составим систему уравнений

0,7Х + 0,6 У = 0,5( Х+У+2) Х = 3

0,7Х+ 0,6У+1,8=0,7( Х+У+2) т.е 3кг.

7Х+6У=5 ( Х+У+2) Ответ . 3

7Х+6У+ 18 = 7 ( Х+У+2)

-18 = -2 ( Х+У+2)

7= Х + У

7Х+6У= 5Х+5 У+10

7=Х+У

10=2Х+У

-3= -Х

Задача №12

Первая труба наполняет бак объемом 600 литров, а вторая труба – бак объемом 900 литров . Известно , что одна из труб пропускает на 3л воды больше ,чем другая. Сколько литров воды в минуту пропускает вторая труба, если баки были наполнены за одно и то же время?

0 900: (Х+3) = 600 :Х 900Х-600Х= 1800 300Х=1800 Х=6 6+3=9 Ответ.9 " width="640"

Решение. Пусть Х - литров в минуту пропускает первая труба, тогда вторая- (Х+3).

Первая труба наполняет бак объемом 600 за 600:Х литров, а вторая труба – бак объемом 900 за 900:(Х+3) литров . а 0

900: (Х+3) = 600 :Х

900Х-600Х= 1800

300Х=1800

Х=6 6+3=9 Ответ.9

Задача №13

В четверг акции компании подорожали на некоторое число процентов, а пятницу подешевели на то же самое число процентов. В результате они стали стоить на 9% дешевле , чем при открытии торгов в четверг. На сколько процентов подорожали акции компании в четверг?

0 1- 0,91 = 0,0001а ² Ответ. 30. а ² = 0,09:0,0001 = 900 " width="640"

Решение

Пусть на а процентов подорожали акции компании в четверг, тогда 100 - 9= 91% .На сколько процентов подорожали акции компании в четверг?

а ∙ (1 + а:100) (1- а:100) = а ∙ 91:100

а ∙ (1- (0,01а )² ) = 0,91 ∙ а

(1- (0,01а )² ) = 0,91

1- 0,0001а ² = 0,91 а = 30 , а 0

1- 0,91 = 0,0001а ² Ответ. 30.

а ² = 0,09:0,0001 = 900

Задача №14

Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали автомобилист и мотоциклист .

Известно , что в час автомобилист проезжает на 90 км больше , чем велосипедист . Определите скорость велосипедиста, если известно , что он прибыл в пункт В на 5 часов 24 минуты позже автомобилиста. Ответ дайте км/ч.

5 часов 24 минуты = 5,4ч

Пусть v соб. велосипедиста = Х км/ч

S ,

v,

t,

км/ч

ч

км

60

Велоси

педист

х

60

х

60

Х+90

Автомо

билист

60

х+90

Составим уравнение.

60

27

60

- =

5

х+90

х

43

Решим уравнение.

60

60

27

- =

5

х

х+90

300 (Х+90) – 300 Х= 27 Х(Х+90)

27Х² +810 Х- 27000= 0

Х² +30 Х- 1000= 0

D = 900+4000= 4900

Х= 20

Х= -50

Ответ .20

44

15. Четыре рубашки дешевле куртки на 8%.На сколько процентов пять рубашек дороже куртки?

• Решение. Обозначим стоимость одной рубашки за Р , тогда К – стоимость одной куртки. Из условия задачи следует, что
• 4Р=К( 100-8)/100
• 4Р= 0,92· К , откуда Р = 0,23·К , и ,следовательно 5Р= 5·0,23·К= 1,15К
• 115 % -100% =15% пять рубашек дороже куртки на 15%. Ответ.15.

Задача №16

Брюки дороже рубашки на 30% и дешевле пиджака на 22%. На сколько процентов рубашка дешевле пиджака?

16.Пусть Хрублей стоят брюки. Так как рубашка на 30% дешевле брюк, то брюки будут дороже рубашки на 30% (величина1+0,3= 1,3), следовательно, стоимость рубашки будет равна. Стоимость брюк на 22% дешевле стоимости пиджака, то есть брюки составляют 100-22=78% от стоимости пиджака, и, следовательно, пиджак стоит стоимость рубашки от стоимости пиджака составляет Х:1,3

Х: 0,78 , т.е 0,6 = 60 %

100 - 60 = 40 % . Ответ. 40.

17.Три килограмма черешни стоят столько же, сколько пять килограммов вишни , а три килограмма вишни – столько же, сколько два килограмма клубники. На сколько процентов килограмм клубники дешевле килограмма черешни?

17. Пусть Х- черешни 1 кг, У- вишни 1 кг, Z- клубники 1кг.Три килограмма черешни стоят столько же, сколько пять килограммов вишни ,т.е 3Х=5 У . а три килограмма вишни – столько же, сколько два килограмма клубники, т.е 3У=2 Z

У= 2/3 Z подставим в уравнение 3Х= 5 У

3 Х = 5 ∙ 2/3 Z

9Х= 10 Z

Z=0 , 9 Х

На 100 - 90= 10% 1 кг клубники

дешевле 1 кг черешни. Ответ 10.

Задача №18

Товарный поезд ,идущий со скоростью 30 км/ч, проезжает мимо придорожного столба за 36 секунд. Определите длину поезда ( в метрах).

30 км/ч = 30000 м : 3600 с = 25 : 3 м/с

1 км = 1000 метров , 1часе = 3600 секунд

Длина поезда 36∙25 : 3=12∙25=300 м

Ответ .300

Задача №19

Из пункта А круговой трассы, длина которой равна 30 км, одновременно в одном направлении стартовали два автомобилиста. Скорость первого равна 92км/ч скорость второго -77 км/ч. Через сколько минут первый автомобилист будет опережать второго ровно на 1 круг?

Решение.

Скорость удаления первого автомобилиста от второго равна

92-77=15 км/ч,

следовательно, первый автомобилист пройдет на 30 км больше второго (то есть обгонит на 1 круг) через 30:15 = 2 часа ,

то есть через 120 минут.

Ответ:  120.

20.Первую половину трассы автомобиль проехал со скоростью 90км/ч, а вторую со скоростью 60км/ч, Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Пусть половина пути равна 1.Пусть все путь S = 1+1= 2 . Время первого 1/90 , а время второго 1/60. Общее время 1/90 + 1/60 = 2/180 +3/180= 5/180.

Средняя скорость равна 2

1/90 + 1/60

V ср. = 2 ∙ 180 = 36 км/ч

5 Ответ. 36

Задача №21

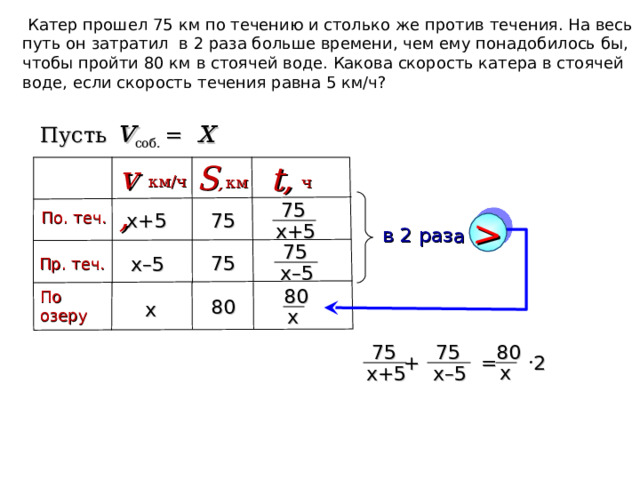
Катер прошел 75 км по течению и столько же против течения. На весь путь он затратил в 2 раза больше времени, чем ему понадобилось бы, чтобы пройти 80 км в стоячей воде. Какова скорость катера в стоячей воде, если скорость течения равна 5 км/ч?

Катер прошел 75 км по течению и столько же против течения. На весь путь он затратил в 2 раза больше времени, чем ему понадобилось бы, чтобы пройти 80 км в стоячей воде. Какова скорость катера в стоячей воде, если скорость течения равна 5 км/ч? Пусть v соб. = x S , v, t, км/ч ч км 75 По. теч. х+5 75 х+5 75 75 х – 5 Пр. теч. х–5 80 По озеру 80 х х 75 80 75 + = 2 х х+5 х–5 " width="640"

в 2 раза

Катер прошел 75 км по течению и столько же против течения. На весь путь он затратил в 2 раза больше времени, чем ему понадобилось бы, чтобы пройти 80 км в стоячей воде. Какова скорость катера в стоячей воде, если скорость течения равна 5 км/ч?

Пусть v соб. = x

S ,

v,

t,

км/ч

ч

км

75

По. теч.

х+5

75

х+5

75

75

х – 5

Пр. теч.

х–5

80

По

озеру

80

х

х

75

80

75

+ =

2

х

х+5

х–5

5 Ответ. 20 56 " width="640"

Решите уравнение .

75

80

75

2

+ =

х

х–5

х+5

15 х (х-5) +15 х ( х+5) = 32 ( Х² -25)

15 Х ² - 75 Х + 15 Х² +75Х = 32 Х ² - 800

32 Х ² -30 Х ² = 800

2 Х ² = 800

Х ² = 400

Х=20

Х= -20 , не удовлетворяет условию Х 5 Ответ. 20

56

Задача №22

Два человека отправились из одного и того же места на прогулку до опушки леса, находящейся в 4,3 км от места отправления. Один идет со скоростью 4 км/ч , а другой – со скоростью 4,6 км/ч . Дойдя до опушки леса, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления

произойдет их встреча?

Задача №23

Города А, В и С соединены прямолинейным шоссе, причем город В расположен между городами А и С.

Из города А в сторону города С выехал легковой автомобиль, и одновременно с ним из города В в сторону города С выехал грузовик. Через сколько часов после выезда легковой автомобиль догонит грузовик , если скорость легкового автомобиля на 28 км/ч больше скорости грузовика , а расстояние между городами А и В равно 112 км?

112: 28 = 4 час.

Самостоятельная работа .

1)Половину времени ,затраченного на дорогу, автомобиль ехал со скоростью 60км/ч, а вторую половину времени – со скоростью 46 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

2) Первая труба наполняет бак объемом 570 литров, а вторая труба- бак объемом 530 литров. Известно, что одна из труб пропускает в минуту на 4л воды больше, чем другая. Сколько литров воды в минуту пропускает вторая труба, если баки были наполнены за одно и тоже время?

1)Половину времени ,затраченного на дорогу, автомобиль ехал со скоростью 60км/ч, а вторую половину времени – со скоростью 46 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Решение.

Обозначим через  половину времени движения автомобиля. Тогда весь пусть составил S = 60 t+46 t= 106 t

Все время в пути составило t+t =2t  . Следовательно, средняя скорость равна Vc р. = 106 t : 2t = 53 км/ч.

  Ответ. 53

2) Первая труба наполняет бак объемом 570 литров, а вторая труба- бак объемом 530 литров. Известно, что одна из труб пропускает в минуту на 4л воды больше, чем другая. Сколько литров воды в минуту пропускает вторая труба, если баки были наполнены за одно и тоже время?

Решение.

Так как баки заполняются за одно и то же время, а объем первого бака 570 литров больше объема второго бака в 530 литров, то пропускная способность первой трубы должна быть больше пропускной способности второй трубы. Обозначим через   Х   пропускную способность второй трубы, тогда первая труба Х+4 будет иметь пропускную способность     литров в минуту. Время заполнения первого бака равно 570 , а у во второй 530

Х+ 4 Х

570 : (Х+4 ) = 530 : Х

57Х=53Х+ 53 · 4

4Х = 212

х= 53

Ответ. 53

24. Баржа проплывает по реке от пристани А до пристани В и вернулись обратно, затратив на путь по течению реки в три раза меньше времени , чем на путь против течения. Во сколько раз скорость течения реки меньше скорости баржи в стоячей воде?

• Так как путь S течению = S против = S. V – скорость баржи в стоячей воде. V₁ - скорость реки.

t ( V + V₁ ) = 3 t (V- V₁) разделим обе части на t

( V + V₁ ) = 3 (V- V₁)

V + V₁ = 3 V- 3V₁

3V₁+V₁ = 3V-V

2 V₁ = 4 V , т.е V₁ = 2 V

Ответ. в 2 раза.

28.Численность волков в двух заповедников в 2009 году составило 220 особей. Через год обнаружили, что в первом заповеднике численность волков возросла на 10% , а во втором – на 20%. В результате общая численность волков в двух заповедника составляет 250 особей . Сколько волков было в первом заповеднике в 2009 году?

В 2008 году в городском квартале проживало 30 000 человек .В 2009 году, в результате строительства новых домов, число жителей выросло на 9%,а в 2010 году- на 10% по сравнению с 2009годом. Сколько человек проживает в квартале в 2010?

• 1) 30000+30000·0,09= 32700 жителей в 2009г.
• 2) 32700+ 32700·0,1= 35970 жителей в 2010г.
• Ответ. 35970

Проверь себя

• Смешали 300г 50%-го и 100г 30%-го раствора кислоты. Определите процентное содержание кислоты в полученной смеси.
• Имеется чай двух сортов – по 80р. И 120р. За 1кг. Смешали 300г первого и 200 г второго сорта. Определите цену 100г полученной смеси.
• Сплавили 2 кг сплава цинка и меди, содержащего 20% цинка, и 6 кг сплава цинка и меди, содержащего 40% цинка. Найдите процентную концентрацию меди в получившемся сплаве .

Проверь себя.

• В сосуде было 12 л чистого спирта. Часть спирта отлили и сосуд долили водой. Затем отлили ещё столько же и опять долили водой. Сколько (в литрах) отливали каждый раз, если в сосуде оказался 25%-й раствор спирта?
• В каждой из двух бочек содержится по 10 вёдер смеси спирта с водой. На 3 части воды приходится в первой бочке 7 частей спирта, а во второй- 2 части спирта. По сколько вёдер нужно взять из этих бочек для составления новой смеси, содержащей спирт и воду в отношении 5:3, чтобы из оставшейся в бочках смеси получить смесь, в которой спирта и воды поровну?
• Имеются два раствора кислоты разной концентрации. Объем одного раствора – 4л, а другого -6л. Если их слить вместе, то получится 35%-ный раствор кислоты. Если же слить равные объемы этих растворов, то получится 36%-ный раствор кислоты. Сколько литров кислоты содержится в каждом из них первоначальных растворов?

Проверь себя.

• У торговца имеется два бочонка вина: емкостью 40л и емкостью 10л. Цены вина за литр различны, но неизвестны. По какому одинаковому количеству вина надо взять из каждого бочонка и перелить в другой бочонок, чтобы цена вина за литр в двух бочонках сравнялась.
• Имеется кусок сплава меди с оловом 12кг содержащий 45% меди. Сколько чистого олова надо прибавить к этому сплаву, чтобы получился новый сплав содержащий 40% меди?
• Из сосуда, содержащего 54л чистой кислоты, вылили несколько литров и после этого долили сосуд водой до прежнего объема. Затем из сосуда вылили смеси столько же литров, как и в первый раз. В результате в смеси, оставшейся в сосуде, осталось чистой кислоты 24л. Сколько кислоты вылили в первый раз?

Литературные источники.

1. Шевкин А.В. Текстовые задачи. 7-11 классы: Учебное пособие по математике. –М.:Русское слово – РС,2005.

2. Шагин В.Л. Вступительные экзамены по математике в Высшей школе экономики,1995-1996. – М.:Вита-Пресс,1998

3. Семёнова А.Л. ЕГЭ 2012. Математика. Типовые экзаменационные варианты. -М.: Национальное образование , 2011.

4. Лебедев В.В.,Михайлов П.А.,Ефимова М.В. Пособие по математике для подготовки к вступительному экзамену в Государственную академию управления. -М.:ГАУ,УЦ «АЗЪ»,1998.

5. Математика, № 6, 2006. (Приложение «1 сентября»).

6. А.Л, Ященко И.В Математика . Типовые тестовые задания 2014-2020