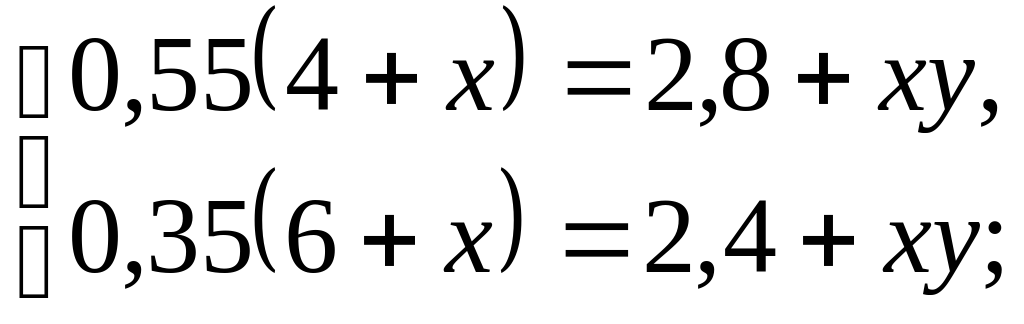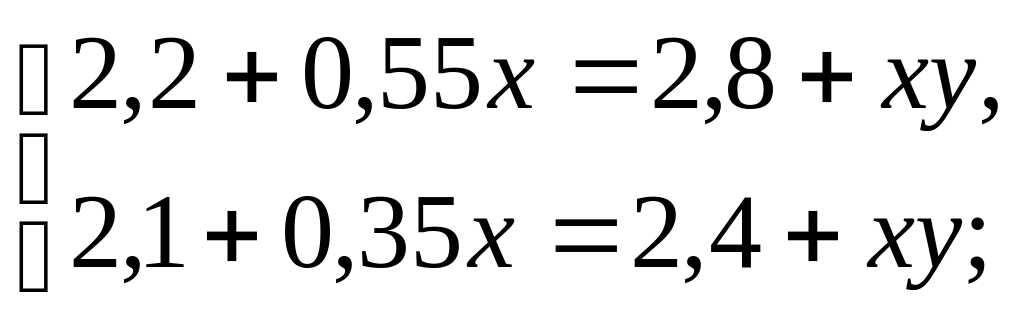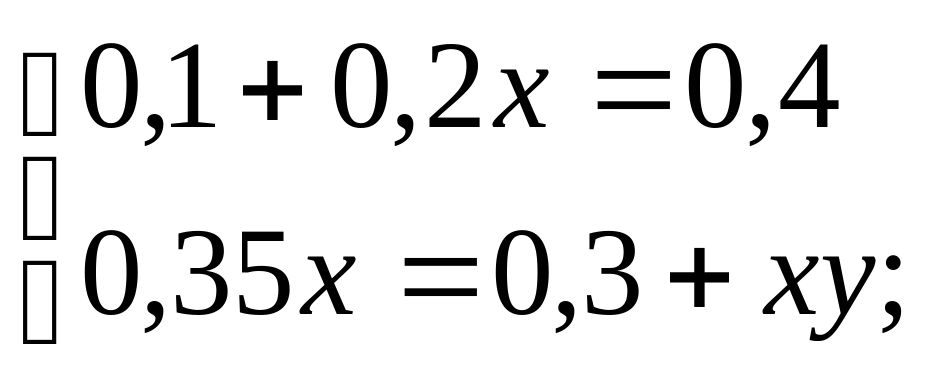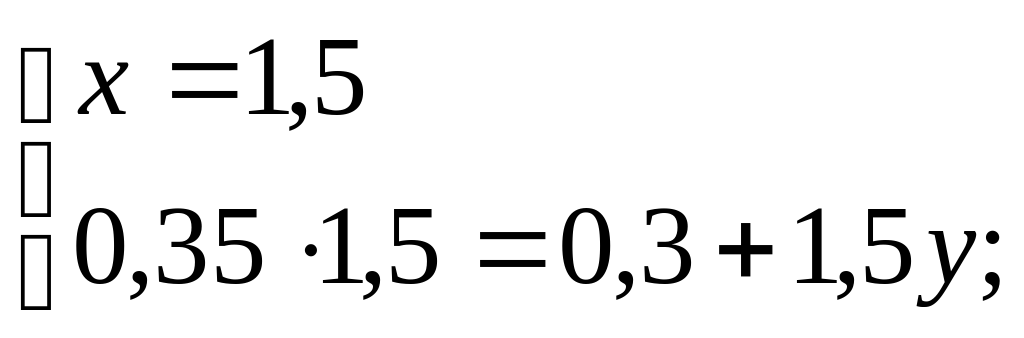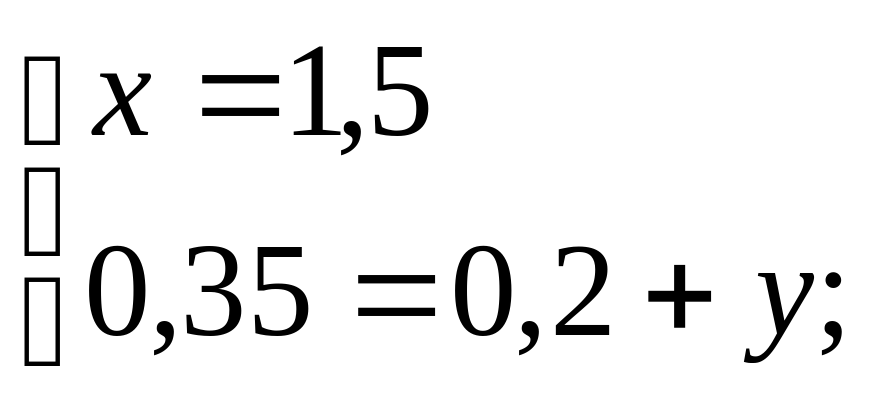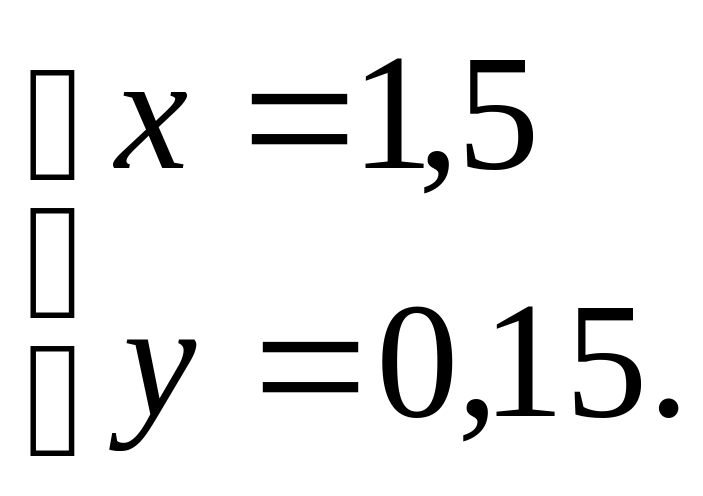Решение задач
на растворы, смеси и сплавы
Содержание
Общие вопросы по теории
Несколько решений одной задачи
Решение задач из ЕГЭ
Введение
В школьном курсе математики практически мало времени уделяется задачам на растворы, смеси и сплавы, хотя в заданиях ОГЭ, ЕГЭ и на олимпиадах по математике они встречаются. При решении задач на растворы, смеси и сплавы можно проверить свои знания по разделам школьной математики, уровень математического и логического мышления, оценить свои способности к математике.
Мною была использована в основном литература для подготовки к ЕГЭ по заданной теме, также несколько вторичных источников и информация, взятая из интернета
Целью моей работы станет предложение нескольких способов решения конкретных задач на концентрацию, смеси и сплавы.
Рассматривая задачи на составление уравнений, остановлюсь прежде всего на тех, решение которых связано с использованием понятий «концентрация» и «процентное содержание». Обычно в условиях таких задач речь идет о составлении сплавов, растворов или смесей двух или нескольких веществ.
Общие вопросы по теории
Основными понятиями в этих задачах являются:
масса или объём раствора (смеси, сплава);
масса или объём вещества входящего в раствор (смесь или в сплав);
концентрация (объёмная или массовая) вещества;
процентное содержание вещества;
доля или часть раствора (смеси, сплава).
Основные допущения, как правило, принимаемые в задачах подобного рода, состоят в следующем:
все смешиваемые вещества не вступают в химическую реакцию, все получающиеся сплавы или смеси однородны;
при слиянии двух растворов, имеющих объемы V1 и V2, получается смесь, объем которой равен V1 + V2, т.е.
V0=V1 + V2,
причем это соотношение является именно допущением, поскольку не всегда выполняется в действительности, например, объём смеси спирта и воды на самом деле несколько меньше суммы объёмов спирта и воды. При слиянии двух растворов не объем, а масса смеси равняется сумме масс составляющих ее компонент:
m0=m1+m2;
закон сохранения объёма или массы имеет место и для отдельных частей (компонентов) раствора, смеси и сплава.
Если первый сплав состоит из нескольких компонентов, например, A, B и C, а второй – из компонентов B, C и D, то новый сплав, полученный при соединении этих двух сплавов, будет содержать компоненты A, B, C, и D, причем массы этих компонентов в новом сплаве равны сумме масс каждого из компонентов, входящих в первый и второй сплавы.
Рассмотрим для определенности смесь трех компонент A, B и C. Объем смеси V0 складывается из объемов чистых компонент:
V0= VA + VB + VC,
а три отношения,
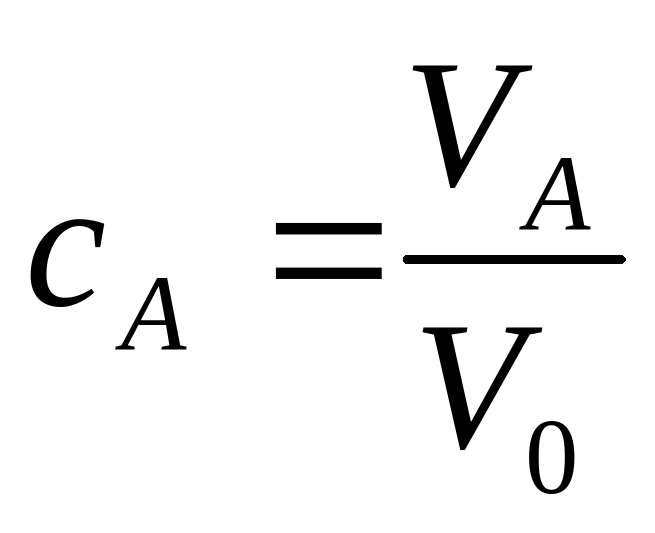 ,
, 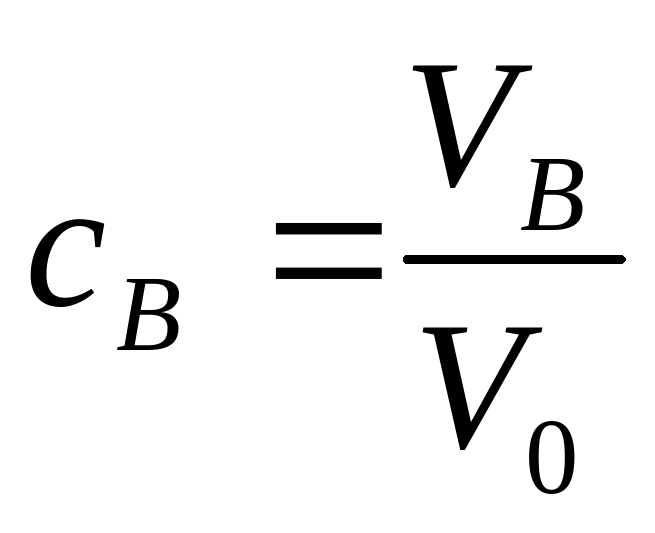 ,
, 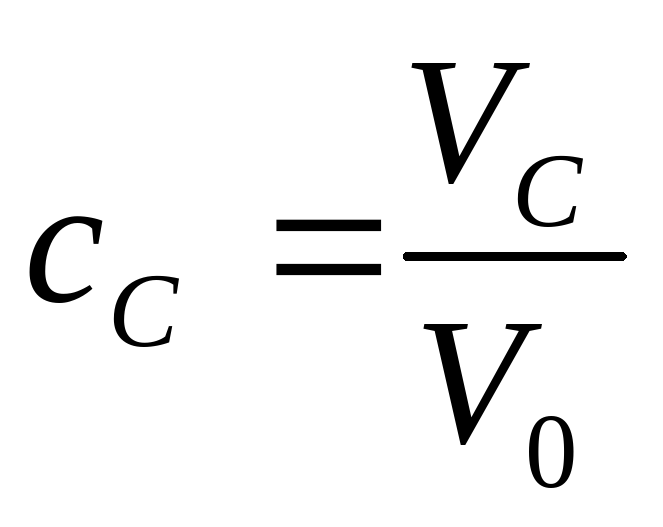 ,
,
показывают, какую долю полного объема смеси составляют объемы отдельных компонент:
VA=cA·V0, VB=cB·V0, VC=cC·V0 .
Отношение объема чистой компоненты (VA) в растворе ко всему объему смеси (V0)
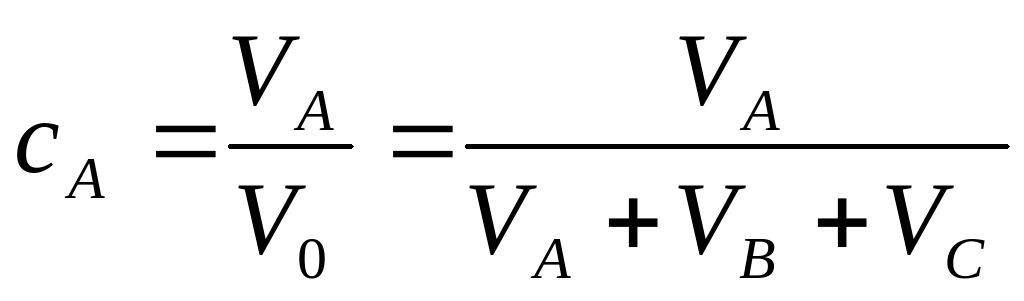
называется объемной концентрацией этой компоненты.
Концентрации – это безмерные величины; сумма концентрации всех компонент, составляющих смесь, очевидно, равна единице:
cA + cB + cC = 1.
Поэтому для того, чтобы структура раствора, состоящего и n компонент, была определена, достаточно знать концентрацию (n-1)-й компоненты.
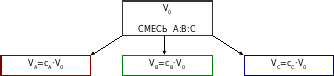
Если известны концентрации cA, cB и cC компонент, составляющих данную смесь, то ее объем можно разбить на объемы отдельных компонент (рис. 1):
V0= cA·V0+ cB·V0+ cC·V0 . (1)
Объемным процентным содержанием компоненты A называется величина pA=cA·100%,
т.е. концентрация этого вещества, выраженная в процентах.
Очевидно pA + pB +pC=100%.
Если известно процентное содержание вещества A, то его концентрация находится по формуле 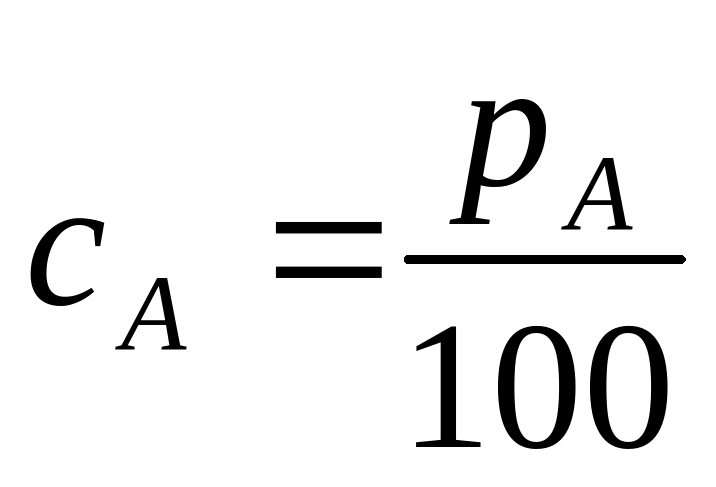 .
.
Так, например, если процентное содержание составляет 80%, то соответствующая концентрация равна 0,8. Процентному содержанию 10% соответствует концентрация 0,1 и т.д.
Таким же способом определяются и массовые концентрация и процентное содержание, а именно, как отношение массы чистого вещества A в сплаве к массе всего сплава. О какой концентрации, объемной или массовой, идет речь в конкретной задаче, всегда ясно из ее условия.
Встречается сравнительно немного задач, в которых приходится пересчитывать объемную концентрацию на массовую или наоборот. Для того чтобы это сделать, необходимо знать плотности компонент, составляющих раствор или сплав. Рассмотрим для примера двухкомпонентную смесь с объемными концентрациями компонент c1 и c2 (c1+c2=1) и плотностями компонент ρ1 и ρ2 . Масса смеси может быть найдена по формуле
M=V1·ρ1+ V2·ρ2=V0·c1 ·ρ1+ V0·c2 ·ρ2,
в которой V1 и V2 – объемы составляющих смесь компонент. Объемные концентрации выражаются друг через друга следующим образом
c1=1-c2 и c2=1-c1 .
Массовые концентрации компонент находятся из равенств
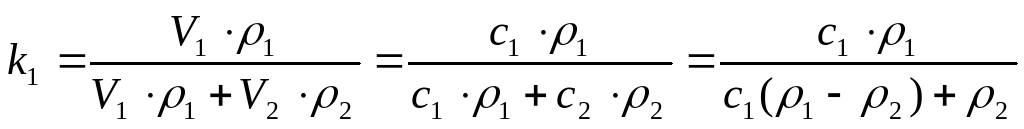 ,
,
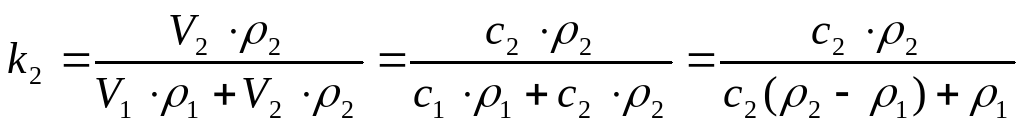 ,
,
которые определяют связь этих величин с объемными концентрациями.
Как правило, в условиях задач рассматриваемого типа встречается один и тот же повторяющийся элемент: из двух или нескольких смесей, содержащих компоненты A1, A2, A3, …, An, составляется новая смесь путем перемешивания исходных смесей, взятых в определенной пропорции. При этом требуется найти, в каком отношении компоненты A1, A2, A3, …, An войдут в получившуюся смесь. Для решения таких задач удобно ввести в рассмотрение объем или массу каждой смеси, а также концентрации составляющих их компонент A1, A2, A3, …, An. С помощью концентраций нужно «расщепить» каждую смесь на отдельные компоненты, как это сделано в формуле (1), а затем указанным в условии задачи способом составить новую смесь. При этом легко подсчитать, какой объем (какая масса) каждой компоненты входит в получившуюся смесь, а также полный объем (полную массу) этой смеси. После этого определяются концентрации компонент A1, A2, A3, …, An в новой смеси.
Несколько решений одной задачи
Задача. Смешали 10%-й раствор серной кислоты с 30%-м раствором той же кислоты. В результате получили 600 г 15%-го раствора серной кислоты. Сколько нужно было взять того и другого раствора?
Решим эту задачу разными способами. Чаще всего при решении пользуются алгебраическим способом. В данном случае можно предложить четыре таких решения.
Первое решение. Пусть нужно взять x г 10%-го раствора, тогда придётся взять (600-x) г 30%-го раствора. Так как в результате смешивания получается 15%-ный раствор, составляем уравнение
0,1x+0,3(600-x)=0,15·600.
Решив это уравнение, получаем ответ: 10%-го раствора - 450 г, 30%-го раствора – 150 г.
Второе решение. Обозначение: требуется взять x г 10%-го раствора, y г 30%-го раствора. На основании условий задачи приходим к простой системе
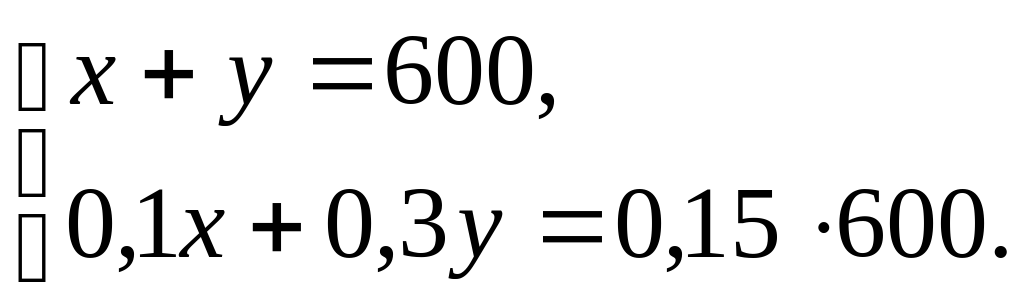
Решая её любым способом либо подстановкой, либо сложением мы найдем те же 450 г и 150 г.
Третье решение. По условию задачи в 600 г раствора должно содержаться 90 г чистой серной кислоты (0,15·600=90). Предположим, что мы взяли бы все 600 г 10%-го раствора. В нём содержалось бы только 60 г серной кислоты (0,1·600=60), т.е. необходимо ещё 30 г. Недостающее количество серной кислоты можно получить, если часть 10%-го раствора заменить более насыщенным 30%-м. Каждый грамм (в силу однородности раствора) 10%-го раствора содержит 0,1 г чистой серной кислоты, а 1 г 30%-го раствора содержит 0,3 г чистой серной кислоты. Таким образом, при замене одного грамма 10%-го раствора на 1 г 30%-го содержание кислоты в растворе увеличивается на 0,2 г. Всего недостает 30 г. Так как 30:0,2=150, значит надо 150 г 10%-го раствора заменить на 150 г 30%-го. Отсюда получаем: 10%-го раствора – 450 г, 30%-го – 150 г.
Ч етвертое решение. Для наглядности рассуждений воспользуемся изображенной на рисунке 5 схемой. В силу однородности растворов в каждой доле полученного 15%-го раствора должно содержаться 15 частей чистой кислоты (это число 15 стоит в центре схемы). Следовательно, каждая доля 10%-го даёт недостачу в 5 частей (- 5), а каждая доля 30%-го раствора даёт избыток в 15 частей (+15). При смешивании избыток и недостаток должны погаситься, поэтому исходные растворы следует брать в отношении, обратном к данному 5:15, т.е. 15:5 или 3:1. Разделив 600г в данном отношении, мы получим искомый ответ: 450г и 150г. Фактически, данный способ позволил решить более общую задачу: каково должно быть соотношение 10%-го и 30%-го растворов, чтобы при смешивании получился 15%-ый раствор.
етвертое решение. Для наглядности рассуждений воспользуемся изображенной на рисунке 5 схемой. В силу однородности растворов в каждой доле полученного 15%-го раствора должно содержаться 15 частей чистой кислоты (это число 15 стоит в центре схемы). Следовательно, каждая доля 10%-го даёт недостачу в 5 частей (- 5), а каждая доля 30%-го раствора даёт избыток в 15 частей (+15). При смешивании избыток и недостаток должны погаситься, поэтому исходные растворы следует брать в отношении, обратном к данному 5:15, т.е. 15:5 или 3:1. Разделив 600г в данном отношении, мы получим искомый ответ: 450г и 150г. Фактически, данный способ позволил решить более общую задачу: каково должно быть соотношение 10%-го и 30%-го растворов, чтобы при смешивании получился 15%-ый раствор.
Решения задач из ЕГЭ
Задача 1. В сосуд, содержащий 180 г 70% -го водного раствора уксуса добавили 320 г воды. Найдите концентрацию получившегося раствора уксусной кислоты.
Решение. Масса уксусной кислоты не изменилась и равна
m1=0,7·180=126 (г).
Получившийся раствор имеет массу
180 г + 320 г = 500 г
Концентрация получившегося раствора уксусной кислоты равна
k=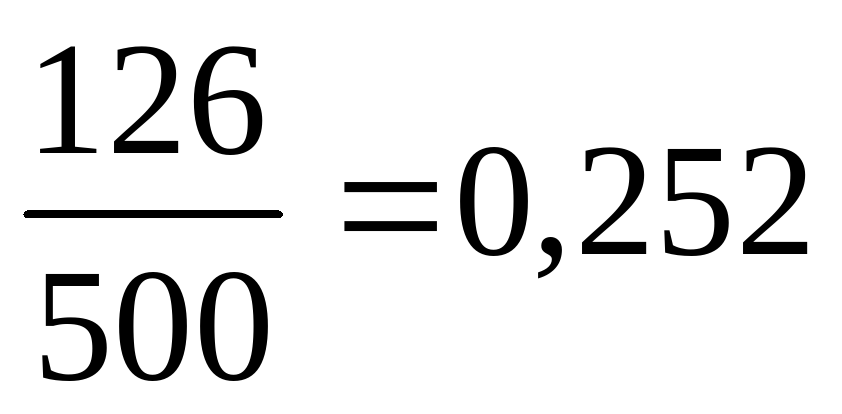 =25,2% Ответ. 25,2%.
=25,2% Ответ. 25,2%.
Задача 2. Сколько нужно добавить воды в сосуд, содержащий 150 г 70% -го раствора уксусной кислоты, чтобы получить 6 % раствор уксусной кислоты?
Решение. Количество воды необходимое для доливания в сосуд обозначим через x.
|
| процентное содержание уксусной кислоты в растворе | Масса раствора г | Масса уксусной кислоты г |
| Исходный раствор | 70% | 150 | 0,7·150=105 |
| Новый раствор | 6% | 150 + x | 0,06(150 + x) |
Так как масса уксусной кислоты осталась прежней, составляем и решаем уравнение
0,06(150 + x) = 105,
9 + 0,06x = 105,
0,06x = 96,
x = 1600.
Ответ. 1,6 кг воды.
Задача 3. Смешали некоторое количество 12% раствора соляной кислоты с таким же количеством 20% раствора этой же кислоты. Найти концентрацию соляной кислоты в получившейся смеси.
Решение. Обозначим: x – концентрация кислоты в смеси, y кг – масса каждого раствора.
|
| Концентрация соляной кислоты в растворе | Масса раствора кг | Масса соляной кислоты кг |
| I раствор | 0,12 | у | 0,12у |
| II раствор | 0,2 | у | 0,2у |
| Смесь | x | 2у | x·2у |
По закону сохранения массы для отдельных компонентов имеем, масса соляной кислоты в смеси равна сумме масс этого вещества, входящих в первый и второй растворы
2xy=0,12y+0,2y.
Из y≠0 следует
2x=0,12+0,2=0,32
x=0,16.
Выражаем в процентах: 16%.
Ответ. 16%
Задача 4. Смешали 8кг 18% раствора некоторого вещества с 12 кг 8% раствора этого же вещества. Найдите концентрацию получившегося раствора.
Решение. Пусть x – концентрация смеси из двух растворов.
|
| Концентрация вещества | Масса раствора кг | Масса вещества кг |
| I раствор | 0,18 | 8 | 0,18·8=1,44 |
| II раствор | 0,08 | 12 | 0,08·12=0,96 |
| Смесь | x | 20 | x·20 |
По закону сохранения массы для отдельного вещества получаем уравнение
20x=1,44+0,96
20x=2,4
x=0,12
или в процентах:12%.
Ответ. 12%
Задача 5. Имеется три сосуда. В первый сосуд налили 4 кг 70% сахарного сиропа, а во второй – 6 кг 40% сахарного сиропа. Если содержимое первого сосуда смешать с содержимым третьего сосуда, то получим в смеси 55% содержание сахара, а если содержимое второго сосуда смешать с третьим, то получим 35% содержание сахара. Найдите массу сахарного сиропа в третьем сосуде и концентрацию сахара в нём.
Решение. Обозначения: x кг - масса сахарного сиропа в третьем сосуде, y – концентрация сахара в нём.
|
| Концентрация сахара | Масса раствора кг | Масса сахара кг |
| Раствор I сосуда | 0,7 | 4 | 0,7·4=2,8 |
| Раствор II сосуда | 0,4 | 6 | 0,4·6 = 2,4 |
| Раствор III сосуда | y | x | xy |
| 1 смесь (содержимое I + III сосуда) | 0,55 | 4+x | 0,55(4+x) |
| 2 смесь (содержимое II +III сосуда) | 0,35 | 6+x | 0,35(6+x) |
По условию задачи составляем уравнения:
для 1 смеси
0,55(4+x)=2,8+ xy,
для 2 смеси
0,35(6+x)=2,4+ xy.
Итак, получаем систему уравнений:
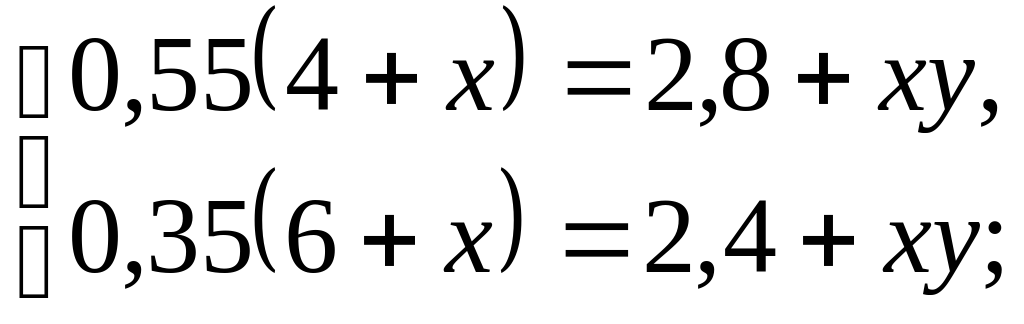
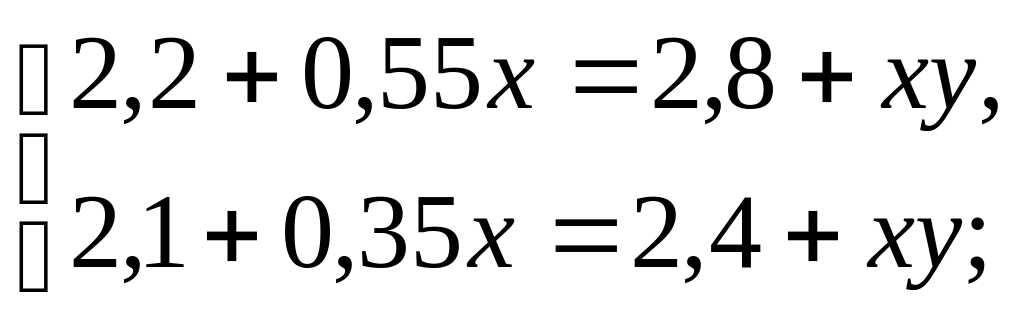
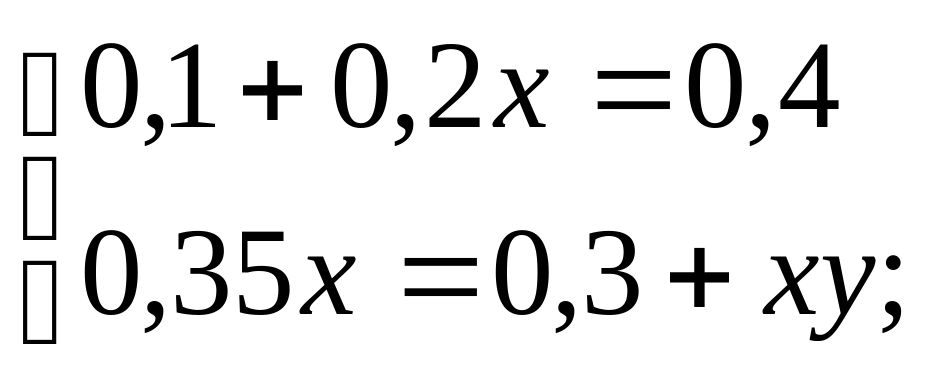
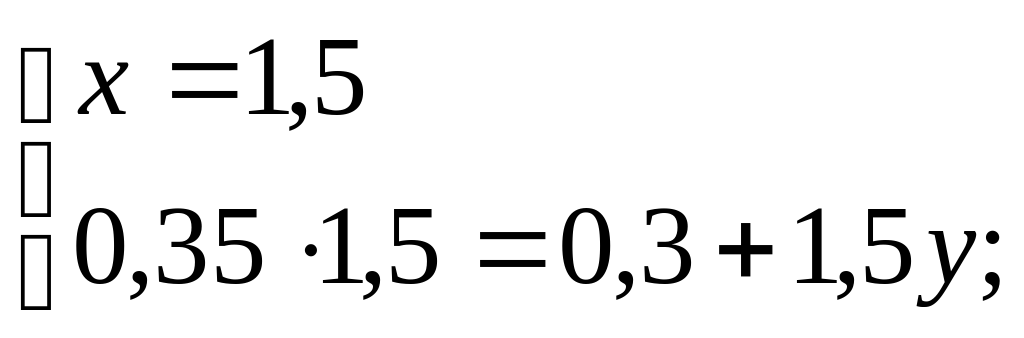
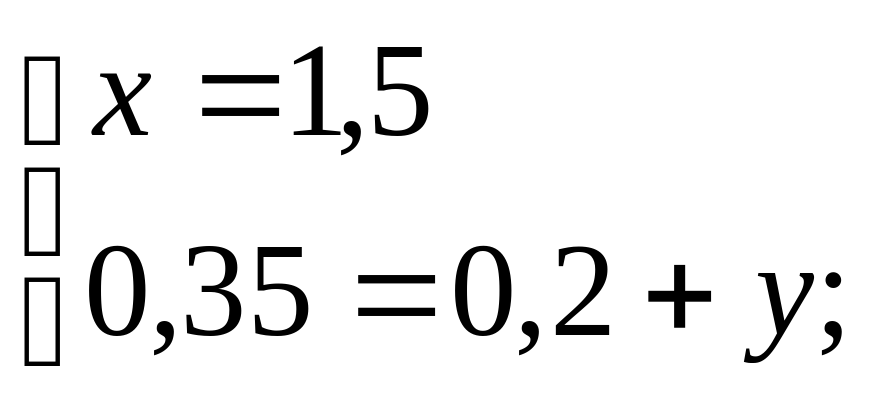
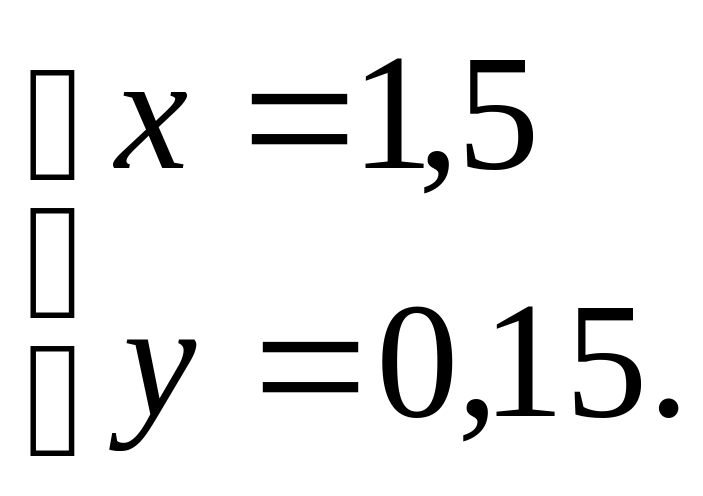
Масса сахарного сиропа в третьем сосуде равна 1,5 кг, а массовое процентное содержание равно 15%.
Ответ. 1,5 кг, 15%.
Задача 6. Имеются два сплава, состоящие из золота и меди. В первом сплаве отношение масс золота и меди равно 8:3, а во втором - 12:5. Сколько килограммов золота и меди содержится в сплаве, приготовленном из 121 кг первого сплава и 255 кг второго сплава?
Решение. Эту задачу можно решить без составления уравнений.
|
| Доля вещества | Масса сплава кг | Масса вещества кг |
| золото | медь | всего | золото | медь |
| I сплав | 8 | 3 | 11 | 121 | 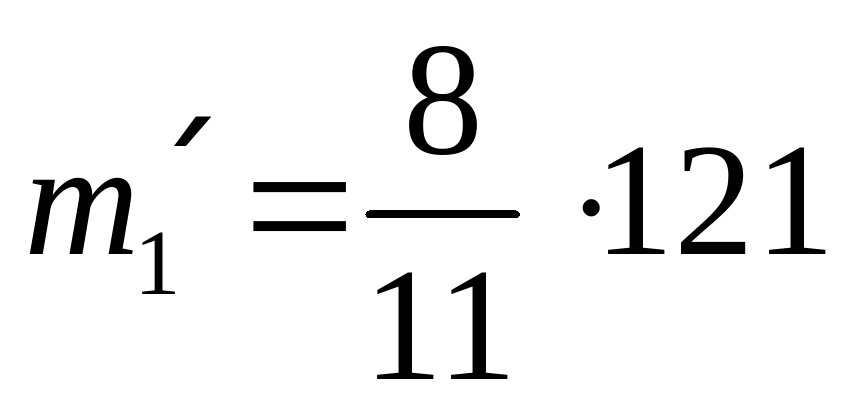
| 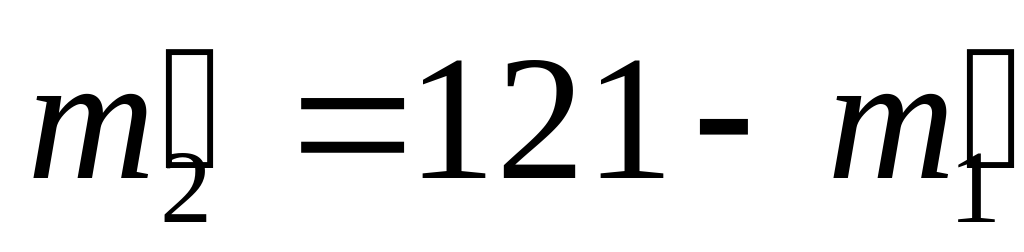 можно не вычислять |
| II сплав | 12 | 5 | 17 | 255 | 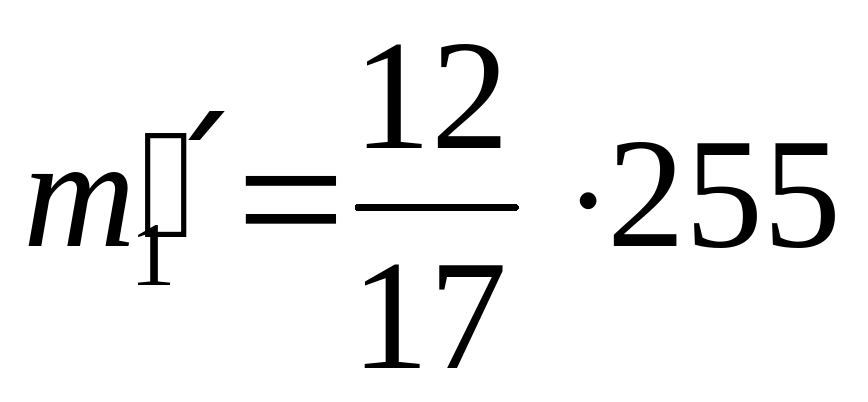
| 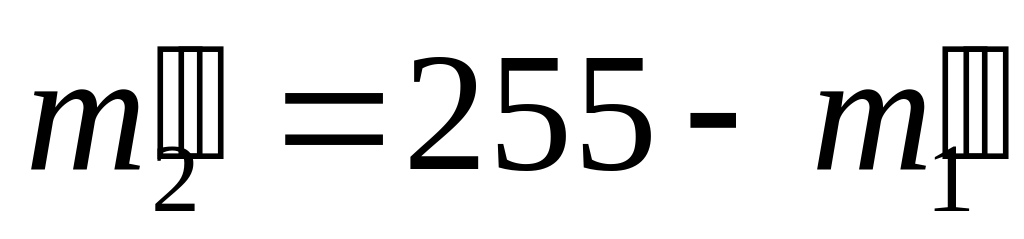 можно не вычислять |
| III сплав | - | - | - | 376 | 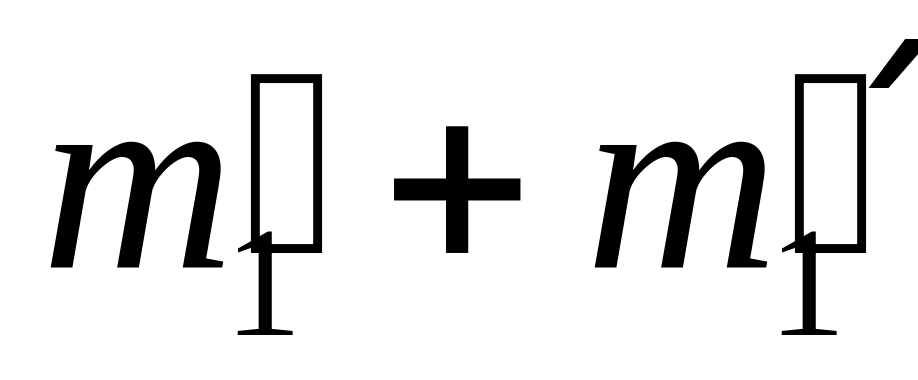
| 
|
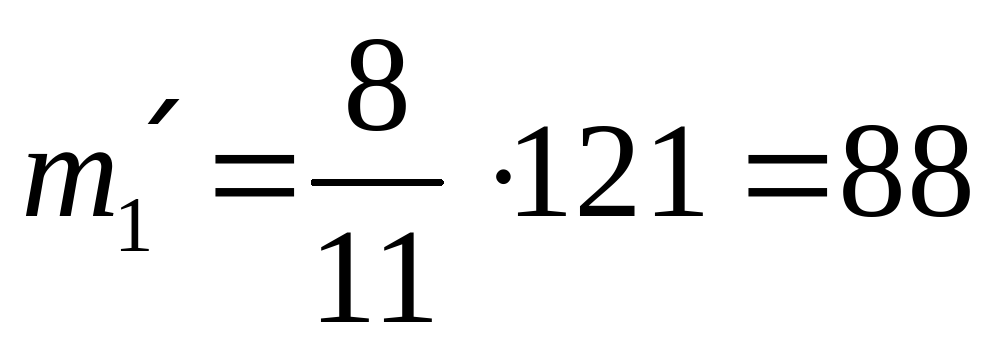 (кг) масса золота в I сплаве,
(кг) масса золота в I сплаве,
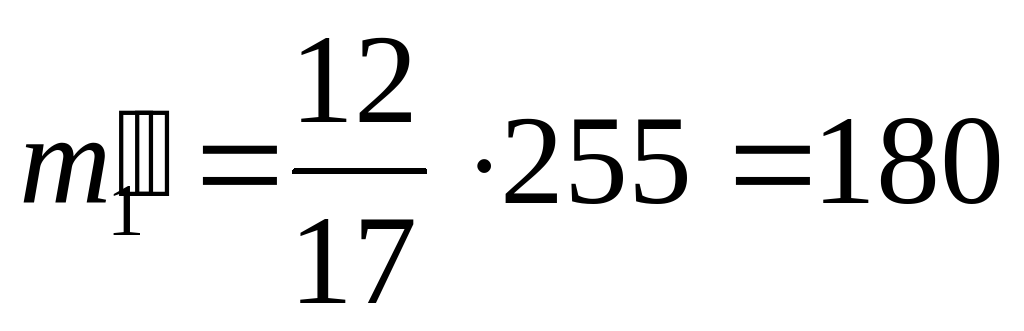 (кг) масса золота в II сплаве,
(кг) масса золота в II сплаве,
121+255=376 (кг) масса III сплава,
88+180=268 (кг) масса золота в III сплаве,
376-268=108 (кг) масса меди в III сплаве.
Ответ. 268 кг золота и 108 кг меди.
Задача 7. При смешивании 5%-го раствора кислоты с 40%-ным раствором той же кислоты получили 140г 30%-го раствора. Сколько граммов каждого раствора было для этого взято?
Решим задачу при помощи схемы. Число 30 ставим в центр схемы. Число 5 ставим в верхнем левом углу схемы, число 40 в правом верхнем углу. Каждая доля 5%-го раствора даёт недостачу в 25 частей (-25), а каждая доля 40%-го раствора даёт избыток в 10 частей (+10). Так как при смешивании недостаток и избыток должны гаситься, то растворы будем брать в отношении обратном к данному 25:10, т.е. 10:25 или 2:5.
5%-го: 140:7·2=40 (г),
40%-го: 140:7·5=100 (г).
Ответ. 40г и 100г.
Задача 8. Имеется два сосуда с 24%-м раствором спирта и 64%-м раствором спирта соответственно. Как можно получить 40%-ый раствор спирта, имея в распоряжении только кружку неизвестной ёмкости и пустой сосуд для смешивания?
Р ешаем при помощи схемы. Из схемы видно, чтобы получить 40%-ый спирт надо взять растворы в отношении 24:16 или 3:2, т.е. необходимо зачерпнуть 3 кружки из сосуда с раствором 24%-м спирта и 2 кружки из сосуда с 64%-м спирта.
Ответ. 3:2.
Заключение
Знание некоторых способов решения задач на концентрацию, смеси и сплавы поможет мне в подготовке к сдаче ЕГЭ по математике, химии и в продолжении образования, а также в профессиональной деятельности. В процессе решения задач на растворы, смеси и сплавы в арсенал приёмов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ, классификация и систематизация, аналогия
Список использованной литературы
1. ЕГЭ Математика. Самостоятельная подготовка к ЕГЭ. Универсальные материалы с методическими рекомендациями, и ответами. Л.Д. Лаппо, М.А. Попов-М., Издательский дом «Экзамен», 2014
2. Учебно-тренировочные материалы для подготовки к единому
государственному экзамену. Математика. Составители: Л.Д.Лаппо, М.А. Попов и др. - М.,: «Экзамен», 2017
3. Математика. 8-9 классы: сборник элективных курсов. Авт. –
сост. В. Н. Студенецкая, Л. С. Сагателова. – Волгоград: «Учитель»,
2007. – 205 с.
4. Сборник задач по математике с решениями. 7-11 кл. Под ред.
М.И.Сканави. – М.: ООО «Издательский дом «ОНИКС 21век»; ООО
Издательство «Мир и Образование», 2003.
5.ОГЭ 2017 . Математика. 9 класс. Тематические тестовые задания. С.С. Минаева, Н.Б. Мельникова – М.,: «Экзамен», 2017








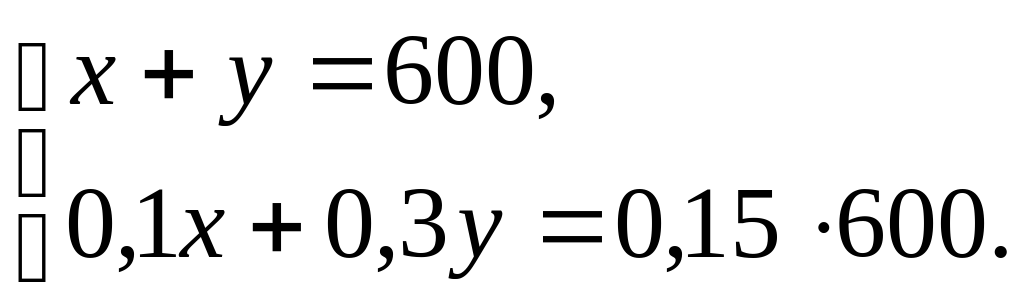
 етвертое решение. Для наглядности рассуждений воспользуемся изображенной на рисунке 5 схемой. В силу однородности растворов в каждой доле полученного 15%-го раствора должно содержаться 15 частей чистой кислоты (это число 15 стоит в центре схемы). Следовательно, каждая доля 10%-го даёт недостачу в 5 частей (- 5), а каждая доля 30%-го раствора даёт избыток в 15 частей (+15). При смешивании избыток и недостаток должны погаситься, поэтому исходные растворы следует брать в отношении, обратном к данному 5:15, т.е. 15:5 или 3:1. Разделив 600г в данном отношении, мы получим искомый ответ: 450г и 150г. Фактически, данный способ позволил решить более общую задачу: каково должно быть соотношение 10%-го и 30%-го растворов, чтобы при смешивании получился 15%-ый раствор.
етвертое решение. Для наглядности рассуждений воспользуемся изображенной на рисунке 5 схемой. В силу однородности растворов в каждой доле полученного 15%-го раствора должно содержаться 15 частей чистой кислоты (это число 15 стоит в центре схемы). Следовательно, каждая доля 10%-го даёт недостачу в 5 частей (- 5), а каждая доля 30%-го раствора даёт избыток в 15 частей (+15). При смешивании избыток и недостаток должны погаситься, поэтому исходные растворы следует брать в отношении, обратном к данному 5:15, т.е. 15:5 или 3:1. Разделив 600г в данном отношении, мы получим искомый ответ: 450г и 150г. Фактически, данный способ позволил решить более общую задачу: каково должно быть соотношение 10%-го и 30%-го растворов, чтобы при смешивании получился 15%-ый раствор.