ГБОУ НАО «СШ №4 г. Нарьян-Мара»
Учитель математики Денисова Ольга Евгеньевна.
Задачи с параметрами,
решение, которых основано на построении графиков функций.
Решение задач с параметрами - один из самых трудных вопросов ЕГЭ. Сложность состоит в индивидуальном подходе к решению такого вида задач и требовании знаний практически всего материала школьной программы.
Задачи с параметрами можно разбить на семь групп:
Задачи с параметрами , в которых требуется найти решение как функцию параметра.
Задачи с параметрами, решение которых основано на использовании свойств линейной и квадратичной функции.
Задачи с параметрами, решение которых основано на симметрии исходных данных.
Задачи с параметрами, решение которых основано на оценках исходных данных.
Задачи с параметрами, которые решаются через дискриминант и теорему Виета.
Задачи с параметрами, решение которых основано на построении графиков функций.
Задачи с параметрами, решение которых использует комбинацию приведённых методов.
Взгляд на параметр как равноправную переменную находит своё отражение в графических методах. Поскольку параметр «равен в правах» с переменной, то ему можно «выделить» свою координатную ось. Таким образом возникает координатная плоскость ( x; a). Такая незначительная деталь , как отказ от традиционного выбора букв х и у для обозначения осей , определяет один из эффективнейших методов решения задач с параметрами. Процесс решения схематично выглядит так. Вначале строится графический образ, затем, пересекая полученный график прямыми, перпендикулярными параметрической оси, «снимаем» нужную информацию.
Графический метод. История возникновения.
Исследование общих зависимостей началось в 14 веке. Средневековая наука была схоластической. Французский ученый Николай Оресм стал изображать интенсивность длинами отрезков. Когда он располагал эти отрезки перпендикулярно некоторой прямой, их концы образовывали линию, названную им "линией интенсивностей" или "линией верхнего края» (график соответствующей функциональной зависимости). Оресм изучал "плоскостные" и "телесные" качества, т.е. функции, зависящие от двух или трех переменных.
Важным достижением Оресма была попытка классифицировать получившиеся графики. Он выделил три типа качеств: Равномерные (с постоянной интенсивностью), равномерно-неравномерные (с постоянной скоростью изменения интенсивности) и неравномерно-неравномерные (все остальные), а также характерные свойства графиков таких качеств.
Чтобы создать математический аппарат для изучения графиков функций, понадобилось понятие переменной величины. Это понятие было введено в науку французским философом и математиком Рене Декартом (1596-1650). Именно Декарт пришел к идеям о единстве алгебры и геометрии и о роли переменных величин, Декарт ввел фиксированный единичный отрезок и стал рассматривать отношения других отрезков к нему.
Таким образом, графики функций за все время своего существования прошли через ряд фундаментальных преобразований, приведших их к тому виду, к которому мы привыкли. Каждый этап или ступень развития графиков функций - неотъемлемая часть истории современной алгебры и геометрии.
Графический способ определения числа корней уравнения в зависимости от входящего в него параметра является более удобным, чем аналитический.
Алгоритм решения графическим методом.
График функции — множество точек, у которых абсциссы являются допустимыми значениями аргумента ![]() , а ординаты — соответствующими значениями функции а (х)
, а ординаты — соответствующими значениями функции а (х)![]() .
.
Алгоритм графического решения уравнений с параметром:
Находим область определения уравнения.
Выражаем α как функцию от х.
В системе координат строим график функции α (х) для тех значений х, которые входят в область определения данного уравнения.
Находим точки пересечения прямой α =с, с графиком функции α (х). Если прямая α =с пересекает график α(х), то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение c = α(х) относительно х.
Записываем ответ
Рассмотрим несколько примеров решения уравнений и неравенств графическим способом.
При всех а решите уравнение x –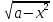 = 1.
= 1.
Найдите все значения параметра а , при каждом из которых уравнение
(а – 6х- 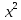 - 5) (а +1 - /х – 3/) = 0
- 5) (а +1 - /х – 3/) = 0
Имеет ровно три различных корня.
При каких значениях а уравнение (а + 4х - 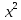 - 1) (а +1 - /х – 2/) = 0
- 1) (а +1 - /х – 2/) = 0
Найти все значения а, при которых система
{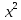 + 2х + а ≤ 0
+ 2х + а ≤ 0
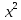 - 4х - 6а ≤ 0 имеет единственное решение.
- 4х - 6а ≤ 0 имеет единственное решение.
Найти все значения а, при которых любое решение неравенства
а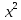 + (1 -
+ (1 - 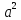 ) х – а 0 по модулю не превосходит двух.
) х – а 0 по модулю не превосходит двух.
При каких значениях а уравнение
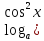 + 1) +
+ 1) + 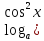 + 5) = 1 .
+ 5) = 1 .
Литература:
И. Г. Тиняков. Задачи с параметрами. М.2001.
П.И. Горнштейн, В.Б. Полонский, М.С. Якир. Задачи с параметрами. «Илекса» 1998.
А.П. Власова, Н. И. Латанова и др. ЕГЭ за 30 дней. МАТЕМАТИКА. Экспресс- репетитор. АСТ: Астрель, 2012.
И.Н. Сергеев. ЕГЭ . Математика. Задания типа С. «Экзамен», 2009.
Учебно - тренировачные тесты пособий « Математика. Подготовка к ЕГЭ»
Решение задач смотри в приложении.
Приложение.
Пример 1. При всех a решите уравнение 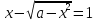 .
.
Решение:
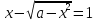
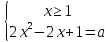
Построим график функции 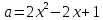 , рассмотрим область x1
, рассмотрим область x1

![]()
x=1
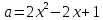
По графику видно, что при a решений нет, при a=1 x=1
А при a1 решение – корень (корни) квадратного уравнения 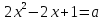 (при x1):
(при x1):
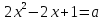
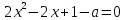
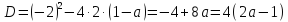
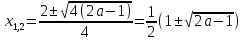
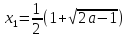
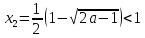 ,при a1 – не является корнем
,при a1 – не является корнем
Ответ: при a - решений нет;
при a=1 x=1;
при a1  .
.
Пример 2. Найдите все значения параметра а, при каждом их которых уравнение имеет ровно три различных корня.
Решение:
| 

| или | 

| Выразим a как функцию от x и построим графики функций |
| |
| (график функции получается смешением на (3; -1) графика функции  ) ) |
![]()
a=-1


из графика видно, что три различных корня получаются при a=-1
Ответ: при a=-1
Пример 3 (для самостоятельного решения). Найдите все значения параметра а, при каждом их которых уравнение имеет ровно три различных корня.
(Ответ: при a=-1)
Пример 4. Найдите все значения a, при которых система имеет единственное решение.
Решение:
Решим систему графически, построив графики функций и
и 
![]()
а=0


а=1
Решением системы неравенств является область между двумя параболами (обозначена зеленым цветом). Таким образом, решение системы имеет единственное решение при a=0 и a=1.
Ответ: a=0, a=1.
Пример 5. Найти все значения a, при которых любое решение неравенства
 по модулю не превосходит двух.
по модулю не превосходит двух.
Решение:




Построим графики функций  и
и 
![]()
a=-0,5
a=-2

x=2
x=-2


Решением первой системы является область, обозначенная желтой штриховкой на рисунке, а второй – зеленой штриховкой.
Условие, что любое решение неравенства не должно превосходить двух означает, что  , графически – решение лежит между прямыми x=-2 и x=2.
, графически – решение лежит между прямыми x=-2 и x=2.
По графику видно, что условие выполняется при 
Ответ:
Пример 6. При каких значениях a уравнение имеет решение?
Решение:

Пусть  , следовательно,
, следовательно, 


Построим график функции a=(c+1)(c+5)


![]()

Из графика следует, что 
Ответ: 
Пример 7. Найдите все значения a при каждом из которых уравнение
имеет более одного корня.
Решение:
![]()
Уравнение имеет единственное решение при  (ордината вершины параболы)
(ордината вершины параболы)
Ответ:
Пример 8. (для самостоятельного решения). Найдите все значения параметра а, при каждом их которых уравнение имеет более трех различных решений. (Ответ: при )
)
Пример 9. (для самостоятельного решения) При каких значениях параметра а уравнения  и
и  имеют общий корень? (Ответ: при
имеют общий корень? (Ответ: при  )
)





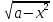 = 1.
= 1.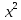 - 5) (а +1 - /х – 3/) = 0
- 5) (а +1 - /х – 3/) = 0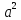 ) х – а 0 по модулю не превосходит двух.
) х – а 0 по модулю не превосходит двух.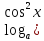 + 1) +
+ 1) + 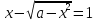 .
.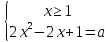
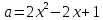 , рассмотрим область x1
, рассмотрим область x1 
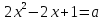 (при x1):
(при x1):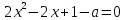
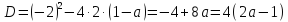
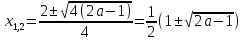
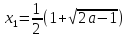
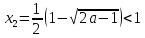 ,при a1 – не является корнем
,при a1 – не является корнем









