Тема «Цикл занятий по подготовке к ЕГЭ по математике (профильный уровень)».
Занятие №4. Решение задачи на оптимальный выбор №16 ЕГЭ по математике.
Формат – мастер-класс
Эффективному постижению азов экономики поможет решение задач, в содержании которых идет речь на оптимальный выбор. Многие школьники не в состоянии воспринимать и понимать речевые обороты взрослых, испытывают затруднения при решении задач экономического характера, а также определить для себя сферу деятельности, профессию в будущем. При решении заданий 16 на оптимальный выбор необходимо составить целевую функцию, описывающую некоторый процесс - функцию оплаты труда, выпуска продукции, распределения ресурсов и пр. При этом необходимо указать ограничения на область определения этой функции. Для нахождения наименьшего или наибольшего значения функции применяем метод исследования функции с помощью производной. Задачи на оптимальный выбор являются практическими задачами. А их решение, бесспорно, способствует более качественному усвоению содержания курса математики средней школы, позволяет осуществлять перенос полученных знаний и умений в экономику, что в свою очередь, активизирует интерес к задачам прикладного характера и изучению математики в целом. Такие задачи позволяют наиболее полно реализовывать прикладную направленность в обучении и способствуют более качественному усвоению самого учебного материала и формированию умения решать задачи данного типа.
Цель мастер – класса:
1)Развивать у учащихся навыки применения теоретических знаний по теме «Производная функции» для решения задач единого государственного экзамена.
2)Обобщить и систематизировать знания учащихся по теме «Производная функции», рассмотреть прототипы задач ЕГЭ по данной теме, предоставить обучающимся возможность проверить свои знания при самостоятельном решении задач.
3) Способствовать развитию памяти, внимания, навыков самооценки и самоконтроля; формированию основных ключевых компетенций (сравнение, сопоставление, контролировать и оценивать свою деятельность, находить и устранять причины возникших трудностей).
4) Способствовать формированию у учащихся ответственного отношения к учению. Методы обучения: словесный, наглядный, практический.
Формы работы: индивидуальная, фронтальная, в парах.
Оборудование и материалы для мастер-класса: проектор, экран, презентация, индивидуально – дифференцированные карточки для самостоятельной работы в парах, список сайтов сети Интернет.
Пояснение к мастер - классу. Данный мастер – класс проводится в 11 классе с целью подготовки к ЕГЭ. В настоящее время важным фактором в обучении старшеклассников является подготовка их к ЕГЭ. Моя методика подготовки основана на подаче базового и теоретического материала и закреплении его на задачах в письменной и интерактивной форме, которая позволяет обеспечить прочное усвоение знаний, умений и навыков, развитие способностей учащихся. Также необходимо показать учащимся алгоритмы решения основных тематических заданий. А вот далее предоставляется свобода ученику в самостоятельной деятельности – повторении и воспроизведении теоретического материала, решении задач. Именно самостоятельная деятельность позволяет обучающемуся раскрыться, лучше использовать свой творческий потенциал, научит применять теоретическую базу при решении различных задач. Системность в работе по подготовке к ЕГЭ предполагает соблюдение следующих принципов: работа на высоком уровне сложности; работа над пониманием формулировки вопроса и умением отвечать строго на поставленный вопрос; работа в соответствии с разработанными алгоритмами выполнения заданий; анализ заданий, вызывающих наибольшие затруднения Целесообразность использования ИКТ: улучшение наглядности изучаемого материала, увеличение количества предлагаемой информации, уменьшение времени подачи материала; повышение эффективности усвоения учебного материала за счет групповой и самостоятельной деятельности учащихся.
Актуальность выбранной темы: при подготовке к ЕГЭ по математике задания №16 вызывают значительные затруднения у выпускников. Это, прежде всего, объясняется неумением учащихся внимательно «вчитываться» в текст задачи. При повторении темы «Производная» следует наряду с овладением навыками вычисления производных добиваться усвоения геометрического и физического смысла производной, умения решать задачи на составление уравнения касательной, исследование функций и вычисление наибольших и наименьших значений. Как правило, учащиеся достаточно прочно овладевают формальными навыками вычисления производных, но задача, требующая понимания геометрического смысла производной, ставит многих из них в тупик.
Список используемой литературы :
Под ред. Ященко И. «ЕГЭ 2024. 50 вариантов. Профильный уровень. Типовые тестовые задания от разработчиков ЕГЭ».
Материалы образовательного порталаhttps://math-ege.sdamgia.ru/
Материалы образовательного портала http://alexlarin.net/ege19.html
Задание №1
В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4t2 у. е. Если на втором объекте работает t человек, то их суточная зарплата составляет t2 у. е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у. е. в этом случае придется заплатить рабочим?
 Решение.
Решение.
Пусть на первый объект будет направлено х рабочих, суточная зарплата которых составит 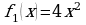 Тогда на второй объект будет направлено
Тогда на второй объект будет направлено 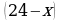 рабочих — суточная заработная плата составит
рабочих — суточная заработная плата составит 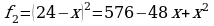 В день начальник будет должен платить рабочим
В день начальник будет должен платить рабочим 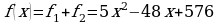 у. е.
у. е.
Рассмотрим функцию 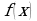 при
при 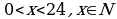 Это квадратичная функция, старший коэффициент положителен, следовательно, она имеет наименьшее значение при x0 = 4,8. Заметим, что точка минимума не является натуральным числом, поэтому исследуемая функция достигает наименьшего значения в точке 4 или в точке 5. Найдем и сравним эти значения:
Это квадратичная функция, старший коэффициент положителен, следовательно, она имеет наименьшее значение при x0 = 4,8. Заметим, что точка минимума не является натуральным числом, поэтому исследуемая функция достигает наименьшего значения в точке 4 или в точке 5. Найдем и сравним эти значения:




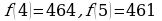

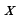
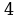
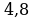
Тем самым, на множестве натуральных значений аргумента наименьшее значение функции достигается в точке 5. Поэтому необходимо направить 5 рабочих на первый объект, 19 рабочих — на второй объект. Зарплата рабочих составит 461 у. е.
Ответ: 5 рабочих на 1-й объект, 19 рабочих на 2-й объект; 461 у.е.
Задание 2
Леонид является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые приборы, но на заводе, расположенном во втором городе, используется более совершенное оборудование.
В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно 4t3 часов в неделю, то за эту неделю они производят t приборов; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t3 часов в неделю, они производят t приборов.
За каждый час работы (на каждом из заводов) Леонид платит рабочему 1 тысячу рублей. Необходимо, чтобы за неделю суммарно производилось 20 приборов. Какую наименьшую сумму придется тратить владельцу заводов еженедельно на оплату труда рабочих?
Решение.
Пусть рабочие первого завода за неделю производят x приборов, второго завода — y приборов. И при этом будет выполнено условие. x + y = 20. Тогда доля человеко-часов, затраченных на первом заводе составит 4x3, а на втором — y3. Таким образом, Леониду придется запланировать на оплату труда рабочих обоих заводов 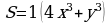 тысяч рублей за неделю. Так как y = 20 − x, то
тысяч рублей за неделю. Так как y = 20 − x, то 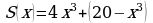 ,
, 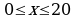 Найдем наименьшее значение функции
Найдем наименьшее значение функции 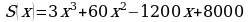 на
на 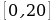
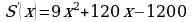

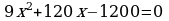
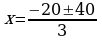
Положительное значение искомого корня 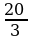 Заметим, что на
Заметим, что на 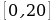 это единственная точка экстремума. Если она окажется точкой минимума функции, то функция именно в этой точке и достигает наименьшего значения.
это единственная точка экстремума. Если она окажется точкой минимума функции, то функция именно в этой точке и достигает наименьшего значения.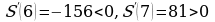 Итак, критическая точка функции точка
Итак, критическая точка функции точка 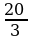 является точкой минимума функции S(x). Поскольку количество изготовленных приборов будет выражаться числом натуральным, то наименьшая сумма, необходимая для выплаты рабочим, будет достигнута либо при x = 6, либо при x = 7.
является точкой минимума функции S(x). Поскольку количество изготовленных приборов будет выражаться числом натуральным, то наименьшая сумма, необходимая для выплаты рабочим, будет достигнута либо при x = 6, либо при x = 7.
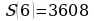 (тысяч руб.);
(тысяч руб.);
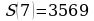 (тысяч руб.)
(тысяч руб.)
Итак, искомая сумма 3 569 000 рублей.
Ответ: 3 569 000 рублей.
Задание 3
Вадим является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно 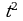 часов в неделю, то за эту неделю они производят t единиц товара.
часов в неделю, то за эту неделю они производят t единиц товара.
За каждый час работы на заводе, расположенном в первом городе, Вадим платит рабочему 200 рублей, а на заводе, расположенном во втором городе, — 300 рублей.
Вадим готов выделять 1 200 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Решение
Допустим, что на заводе, расположенном в первом городе, рабочие трудятся 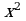 часов, а на заводе, расположенном во втором городе,
часов, а на заводе, расположенном во втором городе, 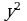 часов. Тогда в неделю будет произведено
часов. Тогда в неделю будет произведено 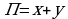 единиц товара, а затраты на оплату труда составят
единиц товара, а затраты на оплату труда составят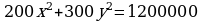 Выразим y через x:
Выразим y через x:
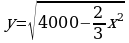 Значит, нам нужно найти наибольшее значение функции
Значит, нам нужно найти наибольшее значение функции 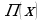 при
при 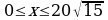 Для этого найдем производную функции
Для этого найдем производную функции 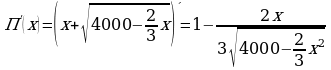
Найдем точки экстремума: 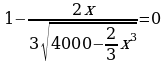
то есть 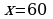 — единственная точка экстремума, удовлетворяющая условию
— единственная точка экстремума, удовлетворяющая условию 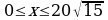 Найдем значения функции в найденной точке и на концах отрезка:
Найдем значения функции в найденной точке и на концах отрезка:
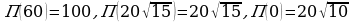
Наибольшее значение функции 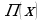 равно 100, значит, наибольшее количество единиц товара равно 100.
равно 100, значит, наибольшее количество единиц товара равно 100.
Ответ: 100.
Задание 4
В двух областях есть по 160 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,1 кг алюминия или 0,1 кг никеля. Во второй области для добычи x кг алюминия в день требуется x2 человеко-часов труда, а для добычи у кг никеля в день требуется у2 человеко-часов труда.
Для нужд промышленности можно использовать или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно за сутки суммарно добыть в двух областях?
Решение.
Поскольку алюминий и никель взаимозаменяемы, а рабочие первой области одинаково эффективно добывают и алюминий, и никель, они могут добывать любой из металлов. За сутки ими будет добыто 160 · 5 · 0,1 = 80 кг металла.
Пусть во второй области алюминий добывают t рабочих, а никель — 160 − t рабочих. Тогда за сутки они добудут 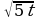 кг алюминия и
кг алюминия и 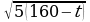 кг никеля. Найдем наибольшее значение функции
кг никеля. Найдем наибольшее значение функции 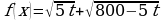 для натуральных t, не больших 160. Имеем:
для натуральных t, не больших 160. Имеем:
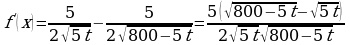
Найдем нули производной: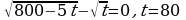
При t меньших 80 производная положительна, а при t больших 80 производная отрицательна, поэтому в точке 80 функция достигает максимума 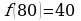 , равного наибольшему значению функции на исследуемом промежутке.
, равного наибольшему значению функции на исследуемом промежутке.
Тем самым, 80 рабочих второй области следует направить на добычу алюминия и 80 — на добычу никеля. Они добудут 40 кг металла. Совместно рабочие первой и второй области добудут 120 кг металла.
Ответ: 120 кг.
Задание 5
В двух шахтах добывают алюминий и никель. В первой шахте имеется 20 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1 кг алюминия или 2 кг никеля. Во второй шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 2 кг алюминия или 1 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
Решение.
Пусть в первой шахте х рабочих, а во второй шахте y рабочих заняты на добыче алюминия. Составим таблицу по данным задачи.
|
| Алюминий | Никель |
| Количество
рабочих, чел | Количество
металла за смену, кг | Количество
рабочих, чел | Количество
металла за смену, кг |
| Шахта 1 | x | 5x | 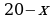
| 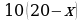
|
| Шахта 2 | y | 10y | 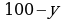
| 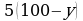
|
| Всего |
| 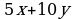
|
| 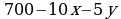
|
Поскольку алюминия необходимо добывать вдвое больше никеля, имеем:
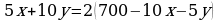 ,
, 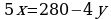 (*)
(*)
Пусть s — масса сплава, она втрое больше массы добытого никеля: 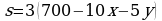 Найдем наибольшее возможное значение этого выражения, подставив в него (*):
Найдем наибольшее возможное значение этого выражения, подставив в него (*):
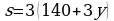
Наибольшему возможному значению s соответствует наибольшее значение y. Из (*) ясно, что наибольшее возможное y равно 70, при этом х = 0, 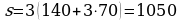 Это означает, что 70 рабочих второй шахты должны быть заняты на добыче алюминия, а оставшиеся 30 рабочих второй шахты и все 20 рабочих первой шахты и должны быть заняты на добыче никеля. При этом они добудут 700 кг алюминия и 350 кг никеля, а масса сплава будет равна 1050 кг.
Это означает, что 70 рабочих второй шахты должны быть заняты на добыче алюминия, а оставшиеся 30 рабочих второй шахты и все 20 рабочих первой шахты и должны быть заняты на добыче никеля. При этом они добудут 700 кг алюминия и 350 кг никеля, а масса сплава будет равна 1050 кг.
Ответ: 1050 кг.
Задание 6
В двух областях есть по 20 рабочих, каждый из которых готов трудиться по 10 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,1 кг алюминия или 0,1 кг никеля. Во второй области для добычи х кг алюминия в день требуется 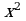 человеко-часов труда, а для добычи у кг никеля в день требуется
человеко-часов труда, а для добычи у кг никеля в день требуется 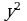 человеко-часов труда.
человеко-часов труда.
Обе области поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 3 кг алюминия приходится 1 кг никеля. При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
Решение.
Пусть в первой области х рабочих заняты на добыче алюминия, а 20 − х рабочих заняты на добыче никеля. Работая 10 часов в сутки, один рабочий добывает 1 кг алюминия или 1 кг никеля, поэтому за сутки рабочие добудут х кг алюминия и (20 − х) кг никеля.
Пусть во второй области у рабочих заняты на добыче алюминия, а 20 − у рабочих заняты на добыче никеля. Работая 10 часов в сутки, n рабочих добывают 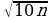 кг любого из металлов, поэтому вместе бригады добудут
кг любого из металлов, поэтому вместе бригады добудут 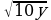 кг алюминия и
кг алюминия и 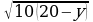 кг никеля.
кг никеля.
Всего будет произведено 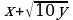 кг алюминия (1) и
кг алюминия (1) и 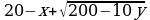 кг никеля (2). Поскольку алюминия необходимо добывать втрое больше никеля, имеем:
кг никеля (2). Поскольку алюминия необходимо добывать втрое больше никеля, имеем:
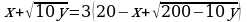 ,
, 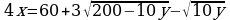 (*)
(*)
Количеству никеля 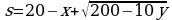 соответствует количество сплава
соответствует количество сплава 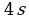 Будем искать наибольшее возможное значение этого выражения, подставив в него (*):
Будем искать наибольшее возможное значение этого выражения, подставив в него (*):
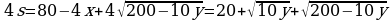
Наибольшему возможному значению s соответствует наибольшее значение функции 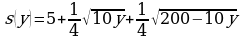 при натуральных y не больших 20.
при натуральных y не больших 20.
Имеем: 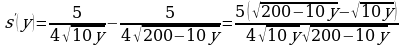
Найдем нули производной:
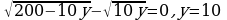
В найденной точке производная меняет знак с плюса на минус, поэтому в ней функция достигает максимума, совпадающего с наибольшим значением функции на исследуемой области.
Далее имеем: 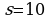 из (*)
из (*) 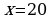 Это означает, что все рабочие первой области должны быть заняты на производстве алюминия, за сутки они произведут его 20 кг, а рабочие второй области бригадами по 10 и 10 человек должны быть заняты на добыче алюминия и никеля, они добудут их по 10 кг. Всего будет добыто 30 кг алюминия и 10 кг никеля, из них будет произведено 40 кг сплава.
Это означает, что все рабочие первой области должны быть заняты на производстве алюминия, за сутки они произведут его 20 кг, а рабочие второй области бригадами по 10 и 10 человек должны быть заняты на добыче алюминия и никеля, они добудут их по 10 кг. Всего будет добыто 30 кг алюминия и 10 кг никеля, из них будет произведено 40 кг сплава.
Ответ: 40 кг.
Задание 7
Производство x тыс. единиц продукции обходится в q = 0,5x2 + x + 7 млн рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет px − q. При каком наименьшем значении p через три года суммарная прибыль составит не менее 75 млн рублей?
Решение.
Прибыль (в млн рублей) за один год выражается величиной
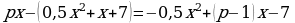
Это выражение является квадратным трёхчленом и достигает своего наибольшего значения 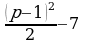 при x = p − 1. Прибыль составит не менее 75 млн рублей, если
при x = p − 1. Прибыль составит не менее 75 млн рублей, если
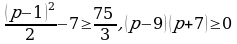
то есть при p ≥ 9, поскольку цена продукции не может быть отрицательной. Таким образом, наименьшее значение p = 9, искомая наименьшая цена 9 тыс. руб.
Ответ: p = 9.
Задание 8
Зависимость объёма Q (в шт.) купленного у фирмы товара от цены Р (в руб. за шт.) выражается формулой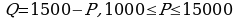 Доход от продажи товара составляет РQ рублей. Затраты на производство Q единиц товара составляют
Доход от продажи товара составляет РQ рублей. Затраты на производство Q единиц товара составляют 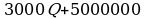 рублей. Прибыль равна разности дохода от продажи товара и затрат на его производство. Стремясь привлечь внимание покупателей, фирма уменьшила цену товара на 20%, однако её прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?
рублей. Прибыль равна разности дохода от продажи товара и затрат на его производство. Стремясь привлечь внимание покупателей, фирма уменьшила цену товара на 20%, однако её прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?
Решение.
Прибыль фирмы выражается как 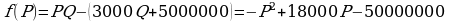 то есть квадратично зависит от цены Р. Пусть первоначальная цена равнялась Р0. После снижения цена стала равняться 0,8Р0. Наибольшая прибыль достигается при значении Р, для которого
то есть квадратично зависит от цены Р. Пусть первоначальная цена равнялась Р0. После снижения цена стала равняться 0,8Р0. Наибольшая прибыль достигается при значении Р, для которого 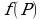 достигает максимума. График функции
достигает максимума. График функции 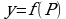 — парабола с ветвями, направленными вниз, поэтому максимум
— парабола с ветвями, направленными вниз, поэтому максимум 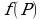 достигается в вершине параболы. Поскольку
достигается в вершине параболы. Поскольку 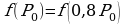 вершина параболы находится в точке
вершина параболы находится в точке 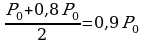 Значит, нужно увеличить цену с 0,8Р0 до 0,9Р0, то есть на 12,5%.
Значит, нужно увеличить цену с 0,8Р0 до 0,9Р0, то есть на 12,5%.
Ответ: 12,5.






 Решение.
Решение.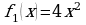 Тогда на второй объект будет направлено
Тогда на второй объект будет направлено 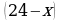 рабочих — суточная заработная плата составит
рабочих — суточная заработная плата составит 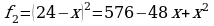 В день начальник будет должен платить рабочим
В день начальник будет должен платить рабочим 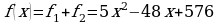 у. е.
у. е.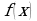 при
при 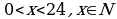 Это квадратичная функция, старший коэффициент положителен, следовательно, она имеет наименьшее значение при x0 = 4,8. Заметим, что точка минимума не является натуральным числом, поэтому исследуемая функция достигает наименьшего значения в точке 4 или в точке 5. Найдем и сравним эти значения:
Это квадратичная функция, старший коэффициент положителен, следовательно, она имеет наименьшее значение при x0 = 4,8. Заметим, что точка минимума не является натуральным числом, поэтому исследуемая функция достигает наименьшего значения в точке 4 или в точке 5. Найдем и сравним эти значения:


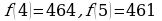

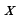
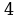
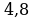
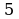
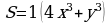 тысяч рублей за неделю. Так как y = 20 − x, то
тысяч рублей за неделю. Так как y = 20 − x, то 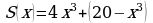 ,
, 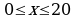 Найдем наименьшее значение функции
Найдем наименьшее значение функции 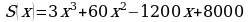 на
на 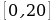
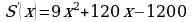
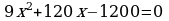
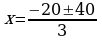
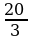 Заметим, что на
Заметим, что на 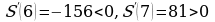 Итак, критическая точка функции точка
Итак, критическая точка функции точка 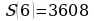 (тысяч руб.);
(тысяч руб.);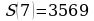 (тысяч руб.)
(тысяч руб.) 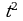 часов в неделю, то за эту неделю они производят t единиц товара.
часов в неделю, то за эту неделю они производят t единиц товара.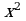 часов, а на заводе, расположенном во втором городе,
часов, а на заводе, расположенном во втором городе, 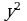 часов. Тогда в неделю будет произведено
часов. Тогда в неделю будет произведено 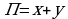 единиц товара, а затраты на оплату труда составят
единиц товара, а затраты на оплату труда составят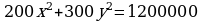 Выразим y через x:
Выразим y через x: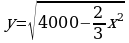 Значит, нам нужно найти наибольшее значение функции
Значит, нам нужно найти наибольшее значение функции 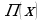 при
при 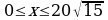 Для этого найдем производную функции
Для этого найдем производную функции 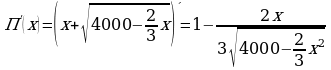
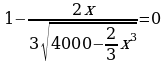
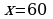 — единственная точка экстремума, удовлетворяющая условию
— единственная точка экстремума, удовлетворяющая условию 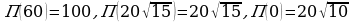
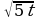 кг алюминия и
кг алюминия и 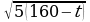 кг никеля. Найдем наибольшее значение функции
кг никеля. Найдем наибольшее значение функции 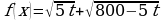 для натуральных t, не больших 160. Имеем:
для натуральных t, не больших 160. Имеем: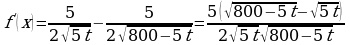
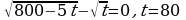
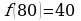 , равного наибольшему значению функции на исследуемом промежутке.
, равного наибольшему значению функции на исследуемом промежутке.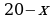
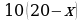
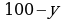
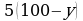
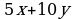
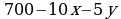
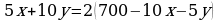 ,
, 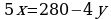 (*)
(*)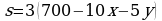 Найдем наибольшее возможное значение этого выражения, подставив в него (*):
Найдем наибольшее возможное значение этого выражения, подставив в него (*):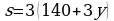
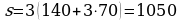 Это означает, что 70 рабочих второй шахты должны быть заняты на добыче алюминия, а оставшиеся 30 рабочих второй шахты и все 20 рабочих первой шахты и должны быть заняты на добыче никеля. При этом они добудут 700 кг алюминия и 350 кг никеля, а масса сплава будет равна 1050 кг.
Это означает, что 70 рабочих второй шахты должны быть заняты на добыче алюминия, а оставшиеся 30 рабочих второй шахты и все 20 рабочих первой шахты и должны быть заняты на добыче никеля. При этом они добудут 700 кг алюминия и 350 кг никеля, а масса сплава будет равна 1050 кг.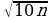 кг любого из металлов, поэтому вместе бригады добудут
кг любого из металлов, поэтому вместе бригады добудут 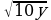 кг алюминия и
кг алюминия и 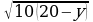 кг никеля.
кг никеля.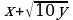 кг алюминия (1) и
кг алюминия (1) и 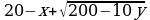 кг никеля (2). Поскольку алюминия необходимо добывать втрое больше никеля, имеем:
кг никеля (2). Поскольку алюминия необходимо добывать втрое больше никеля, имеем: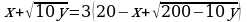 ,
, 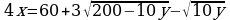 (*)
(*)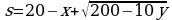 соответствует количество сплава
соответствует количество сплава 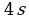 Будем искать наибольшее возможное значение этого выражения, подставив в него (*):
Будем искать наибольшее возможное значение этого выражения, подставив в него (*):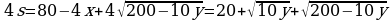
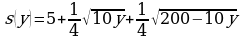 при натуральных y не больших 20.
при натуральных y не больших 20.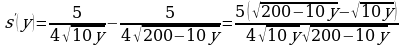
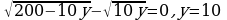
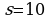 из (*)
из (*) 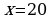 Это означает, что все рабочие первой области должны быть заняты на производстве алюминия, за сутки они произведут его 20 кг, а рабочие второй области бригадами по 10 и 10 человек должны быть заняты на добыче алюминия и никеля, они добудут их по 10 кг. Всего будет добыто 30 кг алюминия и 10 кг никеля, из них будет произведено 40 кг сплава.
Это означает, что все рабочие первой области должны быть заняты на производстве алюминия, за сутки они произведут его 20 кг, а рабочие второй области бригадами по 10 и 10 человек должны быть заняты на добыче алюминия и никеля, они добудут их по 10 кг. Всего будет добыто 30 кг алюминия и 10 кг никеля, из них будет произведено 40 кг сплава.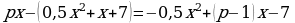
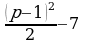 при x = p − 1. Прибыль составит не менее 75 млн рублей, если
при x = p − 1. Прибыль составит не менее 75 млн рублей, если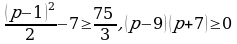
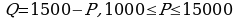 Доход от продажи товара составляет РQ рублей. Затраты на производство Q единиц товара составляют
Доход от продажи товара составляет РQ рублей. Затраты на производство Q единиц товара составляют 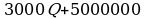 рублей. Прибыль равна разности дохода от продажи товара и затрат на его производство. Стремясь привлечь внимание покупателей, фирма уменьшила цену товара на 20%, однако её прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?
рублей. Прибыль равна разности дохода от продажи товара и затрат на его производство. Стремясь привлечь внимание покупателей, фирма уменьшила цену товара на 20%, однако её прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?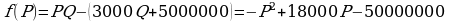 то есть квадратично зависит от цены Р. Пусть первоначальная цена равнялась Р0. После снижения цена стала равняться 0,8Р0. Наибольшая прибыль достигается при значении Р, для которого
то есть квадратично зависит от цены Р. Пусть первоначальная цена равнялась Р0. После снижения цена стала равняться 0,8Р0. Наибольшая прибыль достигается при значении Р, для которого 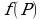 достигает максимума. График функции
достигает максимума. График функции 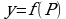 — парабола с ветвями, направленными вниз, поэтому максимум
— парабола с ветвями, направленными вниз, поэтому максимум 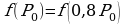 вершина параболы находится в точке
вершина параболы находится в точке 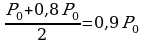 Значит, нужно увеличить цену с 0,8Р0 до 0,9Р0, то есть на 12,5%.
Значит, нужно увеличить цену с 0,8Р0 до 0,9Р0, то есть на 12,5%.









