Как решить систему линейных уравнений?
На данном занятии мы с вами рассмотрим методы решения системы линейных уравнений.
1 способ.
Решение системы линейных уравнений методом подстановки. Пример 1.
В первый день одна бригада работали 7 часов, вторая – 6 часов и собрали вместе 58 ц моркови. Во второй день первая бригада за 3 часа работы собрала на 2 ц меньше, чем вторая бригада за 2 часа. Сколько центнеров моркови собрала каждая бригада за 1 час работы.
Решение.
Обозначим за x и y 1 час работы первой и второй бригады соответственно. Запишем данные задачи в виде системы уравнений.
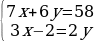
У нас дана система из двух уравнений с двумя неизвестными. Перенесем свободные члены в правую часть.
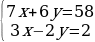
Не забываем, что при переносе слагаемого из одной части в другую у него нужно поменять знак.
Что значит решить систему линейных уравнений?
Решить систему уравнений – это значит найти множество её решений. Решение системы представляет собой набор значений всех входящих в неё переменных, который обращает каждое уравнение системы в верное равенство. Кроме того, система может быть несовместной, т.е. не иметь решений.
Решение:
Что мы должны сделать дальше?
из второго уравнения выразим y: 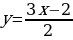 .
.
Полученное выражение подставляем в первое уравнение: 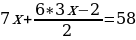
Раскрываем скобки, приводим подобные слагаемые и находим значение x:
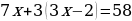

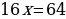
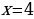 Далее подставим найденное значение x в уравнение:
Далее подставим найденное значение x в уравнение: 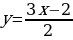 .
.
Осталось найти:  .
. 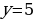
Ответ: 
После того, как решена система уравнений необходимо выполнить проверку.
1) Подставляем найденный ответ  в первое уравнение:
в первое уравнение: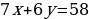
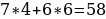 58=58 – получено верное равенство.
58=58 – получено верное равенство.
2) Подставляем найденный ответ во второе уравнение: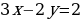
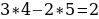 2=2 – получено верное равенство.
2=2 – получено верное равенство.
Рассмотренный способ решения не является единственным, из второго уравнения можно было выразить x, а не y.
Можно наоборот – выразить переменные из первого уравнения и подставить во второе уравнение.
Сегодня мы с вами научимся решать системы линейных уравнений методом Гаусса.
Иоганн Карл Фридрих Гаусс – это немецкий математик, механик, физик, астроном и геодезист. Труды Гаусса оказали большое влияние на развитие алгебры, теории чисел, геометрии, теории электричества и магнетизма и многих разделов астрономии. Еще при жизни он был удостоен почетного титла «принц математиков».
В чем же заключается метод Гаусса?
Метод Гаусса — метод последовательного исключения переменных — заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Рассмотрим данный метод на нашей задаче. У нас дана система уравнений:
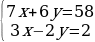
Первое что нам необходимо сделать – это составить матрицу системы.
Матрица – это прямоугольная таблица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: 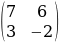 .
.
Составляем расширенную матрицу системы.
 Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае:.
Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае:.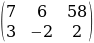 . Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.
. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.
В определении сказано, что матрицу надо привести к ступенчатому виду.
Матрицу называют ступенчатой, если она удовлетворяет таким условиям:
Первый элемент первой строки не равен нулю.
Каждая ненулевая строка (т.е. строка, которая содержит хоть один элемент, не равный нулю) состоит из двух частей: первая часть (нулевая) и вторая часть, которая начинается с ненулевого элемента:
Из двух ненулевых строк та находится ниже, у которой нулевая часть больше.
Нулевые строки могут располагаться только после ненулевых строк.
Какие матрицы на Ваш взгляд ступенчатые, а какие нет?
а)  б)
б) 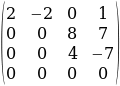 в)
в) 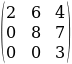 г)
г) 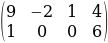
Давайте разберемся по порядку:
а) матрица является ступенчатой, так как первый элемент не нулевой, и вторая строка начинается с нулевого элемента.
Добавлю, что элемент 2 в данной матрице – это первый не нулевой элемент строки, он называется ведущим.
б) матрица не является ступенчатой, поскольку у третьей строки нулевая часть такая же, как и у второй строки, т.е., нарушается принцип "чем ниже строка – тем больше нулевая часть".
в) матрица является ступенчатой, потому что она удовлетворяет всем приведенным критериям.
г) матрица не является ступенчатой, так как во второй строке отсутствует нулевая часть.
Существуют следующие элементарные преобразования:

 Строки матрицы можно переставлять местами. Поменяем в расширенной матрице строки местами:
Строки матрицы можно переставлять местами. Поменяем в расширенной матрице строки местами:  =
= . Тогда в системе
. Тогда в системе 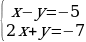 мы поменяем местами два соответственных уравнения
мы поменяем местами два соответственных уравнения  , и совершенно очевидно, что такое преобразование данную систему переведет в равносильную систему.
, и совершенно очевидно, что такое преобразование данную систему переведет в равносильную систему.
Пусть в расширенной матрице имеется нулевая строка. Выбросим ее. Тогда в системе линейных уравнений будет выбрасываться уравнение типа 0 = 0. Такое уравнение, очевидно, удовлетворяется любыми значениями неизвестных, и поэтому это уравнение можно отбросить, не нарушая равносильности системы.
Две системы линейных уравнений называются равносильными, если каждое решение любой из этих систем является решением другой системы.


 Строку матрицы можно умножить (разделить) на любое число, отличное от нуля. Например, дана матрица
Строку матрицы можно умножить (разделить) на любое число, отличное от нуля. Например, дана матрица  Разделим первую строку на –3
Разделим первую строку на –3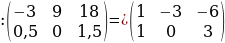 . Так как матрица – это таблица коэффициентов при неизвестных в системе уравнений получим:
. Так как матрица – это таблица коэффициентов при неизвестных в системе уравнений получим:
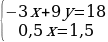 =
=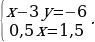
Решим изначальную систему уравнений: x = 3, y = 3. Подставив полученные значения в новую систему видим, что решение первоначальной системы является решением преобразованной системы. Следовательно, полученная система уравнений, будет равносильна исходной системе.

 К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Рассмотрим матрицу:
К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Рассмотрим матрицу:  .
.
 Прибавим ко второй строке расширенной матрицы первую строку, умноженную –2 получим.
Прибавим ко второй строке расширенной матрицы первую строку, умноженную –2 получим. 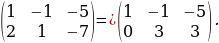
Тогда в преобразованной таким образом системе первое уравнение, будет таким же, что и в первоначальной системе, а второе уравнение примет вид: 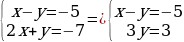
Решив изначальную систему, найдем её решение: x = 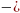 4, y = 1. Подставив в преобразованную систему, увидим, что решение изначальной системы, является решением преобразованной системы. Следовательно, полученная система уравнений, будет равносильна исходной системе.
4, y = 1. Подставив в преобразованную систему, увидим, что решение изначальной системы, является решением преобразованной системы. Следовательно, полученная система уравнений, будет равносильна исходной системе.
Что же нужно сделать, что бы привести матрицу к ступенчатому виду? Давайте запишем алгоритм приведения матрицы к ступенчатому виду.
В первом столбце выбрать ведущий элемент. Строку с ведущим элементом, т.е. ведущую строку, если она не первая, переставить на место первой строки. Если в первом столбце нет ведущего элемента (все элементы равны 0), то исключаем этот столбец, и продолжаем искать ведущий элемент в остальной части матрицы. Преобразования заканчиваются, если все столбцы нашей матрицы исключены или в оставшиеся части матрицы все элементы равны 0.
Разделить все элементы ведущей строки на ведущий элемент. Если ведущая строка последняя, то преобразования закончены.
К каждой строке, расположенной ниже ведущей, прибавить ведущую строку, умноженную на такое число, что все элементы, стоящие под ведущим стали равными нулю.
Исключив из рассмотрения строку и столбец на пересечении которых стоит ведущий элемент, переходим к пункту 1, где все описанные действия применяем к оставшиеся части матрицы.
 Рассмотрим нашу матрицу.
Рассмотрим нашу матрицу. 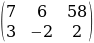 Какой элемент матрицы здесь будет ведущим? 7-это ведущий элемент. Что мы делаем после того, как нашли ведущий элемент?
Какой элемент матрицы здесь будет ведущим? 7-это ведущий элемент. Что мы делаем после того, как нашли ведущий элемент?



 Делим ведущую строку на 7.
Делим ведущую строку на 7. 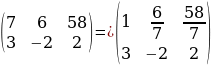 На что умножаем ведущую строку, чтоб под ведущим элементом получить 0. Правильно на -3.
На что умножаем ведущую строку, чтоб под ведущим элементом получить 0. Правильно на -3. 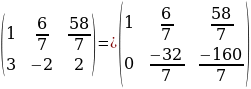
Мы привели матрицу к ступенчатому виду. Что такое элементы матрицы? Элементы матрицы – это коэффициенты при неизвестных переменных системы. Рассмотрим последнюю строку матрицы. Кто может мне сказать, как теперь будет выглядеть наша система?
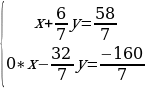
Как можно упростить данную систему?
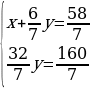
Какие наши дальнейшие действия?
Найдем y из второго уравнения: y = 5
Подставим, найденный y в первое уравнение получим:

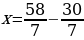
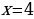
Заметим, что найденные корни системы совпадают с корнями найденными методом подстановки.
Итак, давайте обобщим какие элементарные преобразования над матрицами мы делали.
Давайте рассмотрим следующий пример.
Пример 2.
Три куска сплава имеют общую массу 150 кг. Первый сплав содержит 60% меди, второй – 30%, третий – 10%. При этом во втором и третьем сплавах вместе взятых на 28,4 кг меньше¸ чем в первом сплаве, а в третьем сплаве меди на 6,2 кг меньше, чем во втором. Найти массу каждого куска сплава.
Решение.
Как мы можем обозначить наши переменные?
x – масса первого сплава.
y – масса второго сплава.
z – масса третьего сплава.
Составим систему линейных уравнений:
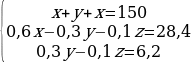
Можно ли как-то упростить данную систему?
Умножим второе и третье уравнение системы на 10.
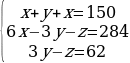
Составим расширенную матрицу системы:

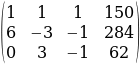
Рассмотрим 1 столбец и выберем ведущий элемент. В данной системе это 1, поэтому переписываем 1 строку. Далее нам нужно получить 0 под ведушим элемонтом. Что мы делаем для этого? Умножаем ведущую строку на – 6 и прибавляем ко второй строке.

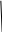
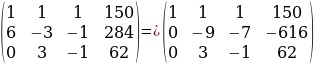
Можно ли как то упростить получнную матрицу?
Умножим 2 строку матрицы на -1.


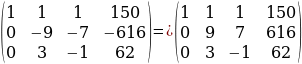
Не рассматривая строку и столбец на пересечение которого стоит ведущий элемент, также находим ведущий элемент. В данном случаи это 9. Умножим третью строку на -3 и прибавим ко второй строке.
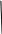

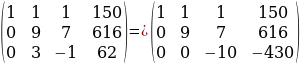
Упростим полученную систму получим.
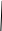

Применем обратный ход метода Гаусса. Находим решение с конца.
Видим, что z = 43.
Из второго уравнения находим y:
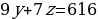
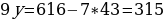
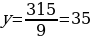
Из третьего уравнения уравнения находим x:
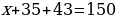
 .
.
Проверку полученных корней сделаете самостоятельно.
Давайте обобщим наши действия, и запишем алгоритм решения систем линейных уравнений методом Гаусса.
Метод Гаусса состоит из двух этапов:
1) «Прямой ход» - с помощью элементарных преобразований привести расширенную матрицу системы линейных алгебраических уравнений к «треугольному» ступенчатому виду.
2) После завершения прямого хода у нас появляется возможность вычислить неизвестную переменную, находящуюся в последнем уравнении. С ее помощью из предпоследнего уравнения находим следующую неизвестную переменную и так далее. Процесс последовательного нахождения неизвестных переменных при движении от последнего уравнения к первому называется «обратным ходом» метода Гаусса.







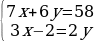
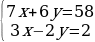
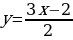 .
. 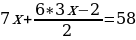
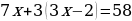

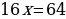
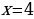 Далее подставим найденное значение x в уравнение:
Далее подставим найденное значение x в уравнение:  .
. 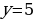

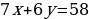
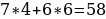 58=58 – получено верное равенство.
58=58 – получено верное равенство.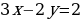
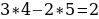 2=2 – получено верное равенство.
2=2 – получено верное равенство.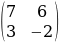 .
. Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае:.
Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае:.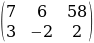 . Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.
. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления. б)
б) 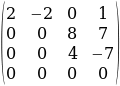 в)
в) 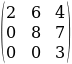 г)
г) 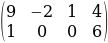

 Строки матрицы можно переставлять местами. Поменяем в расширенной матрице строки местами:
Строки матрицы можно переставлять местами. Поменяем в расширенной матрице строки местами:  =
= . Тогда в системе
. Тогда в системе 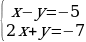 мы поменяем местами два соответственных уравнения
мы поменяем местами два соответственных уравнения  , и совершенно очевидно, что такое преобразование данную систему переведет в равносильную систему.
, и совершенно очевидно, что такое преобразование данную систему переведет в равносильную систему.
 Разделим первую строку на –3
Разделим первую строку на –3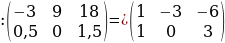 . Так как матрица – это таблица коэффициентов при неизвестных в системе уравнений получим:
. Так как матрица – это таблица коэффициентов при неизвестных в системе уравнений получим: 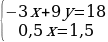 =
=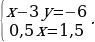
 К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Рассмотрим матрицу:
К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Рассмотрим матрицу:  Прибавим ко второй строке расширенной матрицы первую строку, умноженную –2 получим.
Прибавим ко второй строке расширенной матрицы первую строку, умноженную –2 получим. 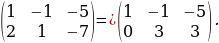
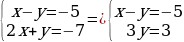
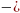 4, y = 1. Подставив в преобразованную систему, увидим, что решение изначальной системы, является решением преобразованной системы. Следовательно, полученная система уравнений, будет равносильна исходной системе.
4, y = 1. Подставив в преобразованную систему, увидим, что решение изначальной системы, является решением преобразованной системы. Следовательно, полученная система уравнений, будет равносильна исходной системе.


 Делим ведущую строку на 7.
Делим ведущую строку на 7. 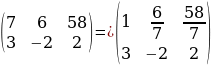 На что умножаем ведущую строку, чтоб под ведущим элементом получить 0. Правильно на -3.
На что умножаем ведущую строку, чтоб под ведущим элементом получить 0. Правильно на -3. 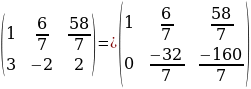
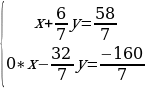
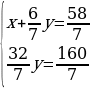

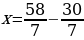
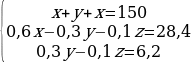
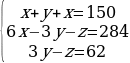

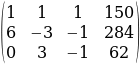
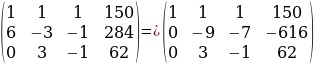

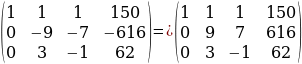
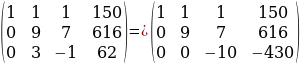

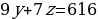
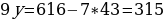
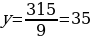
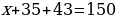
 .
.









