Реляционная модель данных. Реляционная алгебра

Реляционная модель данных. Реляционная алгебра

Основные понятия и определения

Реляционная модель данных (от английского relation — отношение) базируется на математическом аппарате теории множеств и математической логики. Это чрезвычайно мощная и, в отличие от рассмотренных ранее теоретико-графовых моделей, повсеместно применяемая на практике модель данных. Эта модель, где база данных представлена набором n-арных отношений, была предложена Коддом в 1970 г. и за разработку этой модели автор был удостоен премии Тьюринга. Напомним основные понятия и определения, которыми мы будем оперировать в дальнейшем.

n-арным отношением R называют произвольное подмножество декартова произведения D1 x D2 x ... x Dn множеств D1 x D2 x ... x Dn (n≥1). При этом D1 x D2 x ... x Dn называют доменами, а элемент отношения — кортежем. С математической точки зрения отношение может быть бесконечным множеством, однако в реляционных моделях его предполагают конечным.

Домены Di и Dj, которые служат основой для задания одного отношения, могут быть одним и тем же множеством. Чтобы различать эти множества Di, им присваиваются имена и называют их именами атрибутов или просто атрибутами. Количество атрибутов в отношении называется степенью или арностью отношения.

Рассмотрим простейший пример отношения. Пусть даны 3 домена D1 — домен, который содержит перечень возможных должностей на конкретном предприятии. Домен — это множество, поэтому задать множество можно перечислением его элементов, например D1={директор, системный администратор, менеджер, бухгалтер}. Здесь фигурные скобки используются для задания множества. Внутри фигурных скобок содержится список элементов множества. Элементы отделены друг от друга запятой, которая здесь играет роль стандартного разделителя. Домен D2 содержит список фамилий сотрудников нашей организации. Допустим, что данный домен состоит из пяти элементов, что может быть представлено следующим образом: D2={Архипов А. А., Бушков  В. А., Логинова  Н. А., Михайлов  А. П., Смирнова  Т. В.}. И, наконец, третий домен D3 содержит перечень окладов. Пусть содержание этого домена будет D3={20 000, 25 000, 30 000}.

Декартово произведение доменов — это тоже множество, поэтому мы для его представления также можем использовать фигурные скобки. Однако следует отметить, что элементами являются уже не отдельные значения, а так называемые n-ки, т. е. элементы, каждый из которых состоит из n компонент. Для изображения таких элементов в математике широко используются угловые скобки, внутри которых перечисляются отдельные компоненты. А почему угловые скобки? Ведь угловые скобки чаще всего используются для изображения векторов. А почему нам не использовать круглые скобки? Круглые скобки в математике чаще используются для изображения составных элементов, которые включают в себя совокупность однородных объектов, в то время как угловые скобки используются для изображения объектов, которые состоят из разнородных объектов. И в нашем случае каждый составной объект включает в себя элементарные значения, принадлежащие разным доменам.

Итак имеем 3 исходных домена:

D1={директор, системный администратор, менеджер, бухгалтер};

D2={Архипов А. А., Бушков  В. А., Логинова  Н. А., Михайлов  А. П., Смирнова  Т. В.};

D3={20000, 25000, 30000}.

Тогда полное декартово произведение будет содержать следующие тройки элементов:

D1 x D2 x D3 ={, ,,,,,,,,, ,, ...}. Всего таких троек будет 60. Это число получается как произведение мощностей всех исходных множеств-доменов: 4 × 5 х 3 = 60. Но на самом деле мы знаем, что достоверными будут только 5 записей из всех 60, потому что для 5 сотрудников будут заданы реальные должности и оклады. Вот именно эти реальные 5 записей и составят содержание отношения. В этом случае отношение может быть представлено в виде следующего множества:

R={, , , , }.

Любое отношение имеет простую графическую интерпретацию: оно может быть изображено с помощью таблицы: столбцами таблицы являются атрибуты, а строками таблицы являются наши n-ки, которые в реляционной модели называются кортежами 

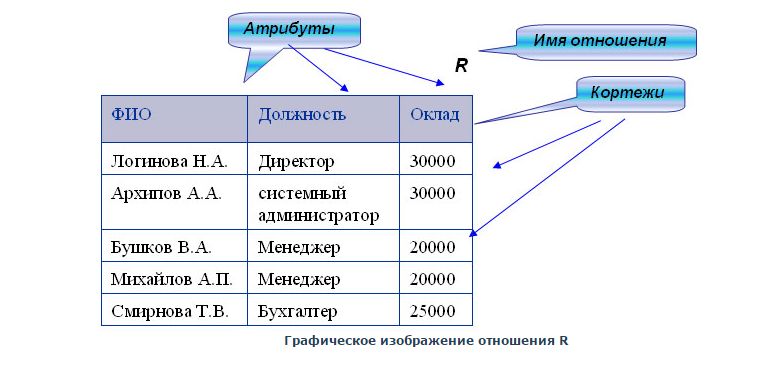
Количество атрибутов в отношении называется степенью или арностью отношения. Отношения со степенью 2 и 3 имеют специальные названия: бинарные и тернарные соответственно. Все остальные отношения просто характеризуются как «отношение R1 степени 5». Например, наше отношение R имеет степень 3, поэтому может быть названо тернарным отношением.

Таблица, которая соответствует отношению, имеет ряд особенностей:

1. В таблице не может быть двух одинаковых строк.

2. Таблица имеет столбцы, соответствующие атрибутам отношения.

3. Каждый атрибут в отношении имеет уникальное имя.

4. Порядок строк в таблице произвольный.

В общем случае можно сказать, что и порядок столбцов в таблице произвольный, потому что для каждого столбца-атрибута задается домен, из которого этот атрибут принимает значения и это соответствие закрепляется понятием схемы отношения.

Схемой отношения R называется перечень имен атрибутов данного отношения с указанием домена, к которому они относятся. Например, схему нашего отношения можно задать следующим образом:

.

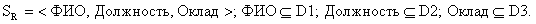Атрибуты, которые принимают значения из одного и того же домена, называются Θ-сравнимыми. Здесь Θ — одна из допустимых операций сравнения Θ = {=, ,=,}. Если мы имеем дело с символьными данными, то мы можем использовать только операции «равно», «не равно» в качестве операций сравнения. Однако если в домене, который содержит, например, список фамилий, допустимо лексико-графическое упорядочение, то тогда мы можем использовать полный спектр операций сравнения.

В общем случае в определении отношения не установлено ограничение на то, что все домены в исходном множестве должны быть различные. Атрибуты в отношении все должны иметь уникальные имена, но при этом в одном отношении могут быть и Θ-сравнимые атрибуты. Приведем пример такого отношения (рис. 2.2).

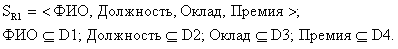
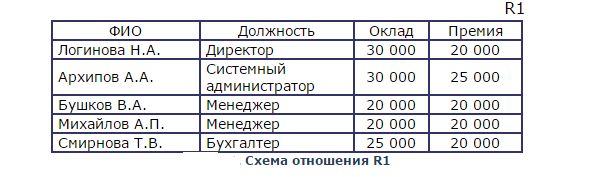
Здесь атрибуты «Оклад» и «Премия» являются Θ-сравнимыми.

Два отношения R1 и R2 называются отношениями с эквивалентными схемами тогда и только тогда, когда они имеют одинаковую степень (арность) и существует такая перестановка атрибутов в схеме отношения R2, что на одинаковых местах в схемах отношений будут стоять Θ-сравнимые атрибуты. Рассмотрим пример (рис. 2.3). Пусть даны 3 отношения: R1,R2,R3.. В первом отношении пусть содержится список абитуриентов и год их рождения, во втором так же список абитуриентов и номер школы, которую они закончили. В третьем отношении находится список абитуриентов с указанием года окончания школы.

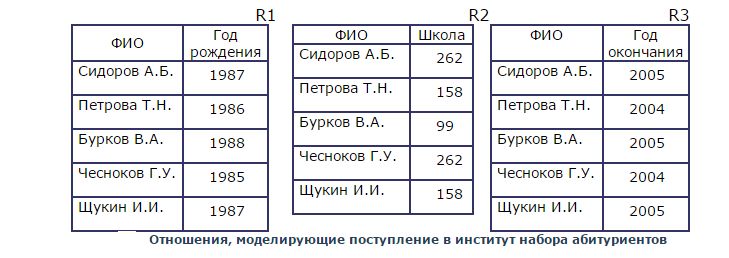
В нашем примере все три отношения имеют одинаковый ранг — они являются бинарными, в каждом из них первый атрибут принимает значения из домена, содержащего фамилии абитуриентов, а второй атрибут принимает значения из множества целых чисел. Однако следует отметить, что отношение R2 содержит список школ и этот столбец по смыслу не принимает значения из домена, в котором содержатся годы. На основании проведенного анализа можно сказать, что отношения R1 и R2 являются отношениями с эквивалентными схемами, а отношение R3 не является таковым по отношению к R1 и R2.

Как уже говорилось ранее, реляционная модель представляет базу данных в виде множества взаимосвязанных отношений.

Мы уже отметили, что каждое отношение имеет только различные кортежи. Это свойство означает, что в отношении обязательно присутствует некоторый набор атрибутов, однозначно определяющий кортеж отношения. В крайнем случае это будет полный набор атрибутов. А в общем случае это может быть и один какой-то атрибут. Этот набор атрибутов называется возможным ключом отношения. У нас в отношении R1 таким набором является атрибут «Фамилия». Если мы рассмотрим отношение, которое моделирует сессию, при этом будем считать, что студент может делать несколько попыток сдачи экзаменов, и при этом фиксируется каждая произведенная попытка, то структура отношения Session будет иметь следующий вид

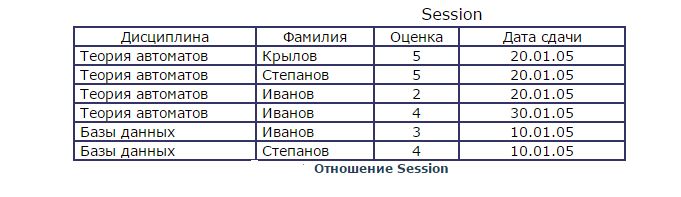
Для данного отношения атрибут «Фамилия» не является возможным ключом отношения, каждый студент может сдавать несколько дисциплин в сессию, и он даже может одну и ту же дисциплину сдавать несколько раз, пока не получит положительную оценку. В данном отношении возможным ключом является набор из трех атрибутов («Фамилия», «Дисциплина», «Дата сдачи»).

В отношении может быть несколько возможных ключей. Среди всех возможных ключей выбирается один, который называется первичным ключом отношения (PRIMARY KEY). Задание первичного ключа — процесс очень важный, он в дальнейшем позволит СУБД обеспечить максимально быстрый доступ именно по данному набору атрибутов. Поэтому к выбору первичного ключа необходимо подходить очень внимательно.

Как уже говорилось ранее, реляционная модель представляет базу данных в виде множества взаимосвязанных отношений. В отличие от теоретико-графовых моделей в реляционной модели связи между отношениями поддерживаются неявным образом. В этой модели так же, как и в остальных, поддерживаются иерархические связи между отношениями. В каждой связи одно отношение может выступать как основное, а другое отношение — в роли подчиненного. Это означает, что один кортеж основного отношения может быть связан с несколькими кортежами подчиненного отношения. Для поддержки этих связей оба отношения должны содержать наборы атрибутов, по которым они связаны. В основном отношении это первичный ключ отношения (PRIMARY KEY), который однозначно определяет кортеж основного отношения. В подчиненном отношении для моделирования связи должен присутствовать набор атрибутов, соответствующий первичному ключу основного отношения. Однако здесь этот набор атрибутов уже является вторичным ключом, т. е. он определяет множество кортежей подчиненного отношения, которые связаны с единственным кортежем основного отношения. Данный набор атрибутов в подчиненном отношении принято называть внешним ключом (FOREIGN KEY).

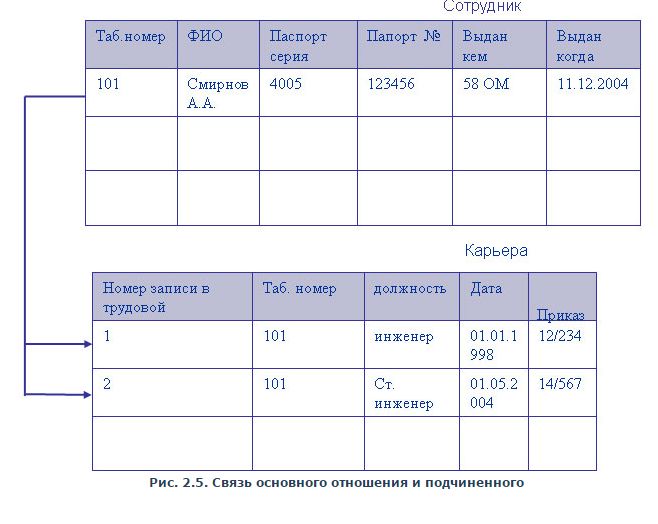
Например, рассмотрим ситуацию, когда надо описать карьеру некоторого индивидуума. Каждый человек в своей трудовой деятельности сменяет несколько мест работы в разных организациях, где он работает в разных должностях. Тогда мы должны создать два отношения: одно для моделирования всех работающих людей, а другое для моделирования записей в их трудовых книжках, если для нас важно не только отследить переход работника из одной организации в другую, но и прохождение его по служебной лестнице в рамках одной организации

В отношении «Сотрудник» атрибут «Таб. номер» является первичным ключом (PRIMARY KEY). В отношении «Карьера» атрибут «Таб. номер» является внешним ключом (FOREIGN KEY), а первичным ключом отношения «Карьера» будет набор атрибутов «Номер записи в трудовой книжке», «Таб. номер». В общем случае отношение может выступать в роли основного по отношению к другому и в роли подчиненного к некоторому третьему отношению. Следует отметить, что одно отношение может быть подчинено сразу нескольким основным отношениям, в этом случае в нем присутствуют сразу несколько внешних ключей, а вот первичный ключ отношения всегда только один.

Реляционная алгебра

Напомним, что алгеброй называется множество с заданной на нем совокупностью операций, замкнутых относительно этого множества, называемого основным множеством. Свойство замкнутости интерпретируется как принадлежность результатов выполнения операций основному множеству.

Основным множеством в реляционной алгебре является множество отношений. Следовательно, результатом выполнения любой алгебраической операции является также отношение.

Автор реляционной модели Э. Ф. Кодд при описании реляционной алгебры ограничил набор операций в ней семью основными и одной дополнительной операциями. Эти семь операций можно разделить на две группы: теоретико-множественные операции и специальные операции. В первую группу входят 4 бинарные операции, т. е. операции, которые применяются к двум операндам (исходным отношениям). Первые 3 теоретико-множественные операции применяются только к отношениям с эквивалентными схемами.

Пусть заданы два отношения R1 = { r1 }, R2 = { r2 }, где r1 и r2 — соответственно кортежи отношений R1 и R2. Мы рассматриваем каждое отношение как множество кортежей, а маленькие буквы r1 и r2 мы использовали для обозначения элемента каждого множества. Соответственно схемы отношений S_R1 и S_R2. При этом отношения R1 и R2 имеют эквивалентные схемы, т. е. S_R1∞S_R2. Тогда для них допустимы следующие операции: объединение, пересечение и разность.

Объединением двух отношений называется отношение, содержащее множество кортежей, принадлежащих либо первому, либо второму исходным отношениям, либо обоим отношениям одновременно.

Для отношений R1 и R2 отношение R3 — это множество всех кортежей, содержащее кортежи из R 1 и R 2: 

.

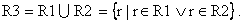Так как отношение не может содержать одинаковых кортежей, то все дубликаты кортежей, уничтожаются, они присутствуют в результирующем отношении только один раз. В фигурных скобках так же находится множество, но в данном случае для задания множества принят не простой способ перечисления элементов множества, а задание некоторого правила, которое определяет принадлежность элементов к заданному множеству. В нашем случае правило представлено в виде записи, разделенной вертикальной чертой на две части: до четы дано обобщенное имя элемента множества, а после черты дается правило, позволяющее определить условия принадлежности конкретного элемента к множеству. Наше правило может быть изложено в виде некоторого повествовательного предложения следующего содержания: «В множество входят элементы r, которые принадлежат либо исходному множеству R1, либо исходному множеству R2». Знак ν соответствует логической операции «ИЛИ».

Рассмотрим следующий пример. Пусть заданы отношения, которые моделируют номенклатуру изделий, изготавливаемых в первом филиале (R1) и во втором филиале фирмы (R2). Тогда объединение данных отношений позволяет получить общую номенклатуру изделий, которые производятся в данной фирме. Это будет отношение R3 

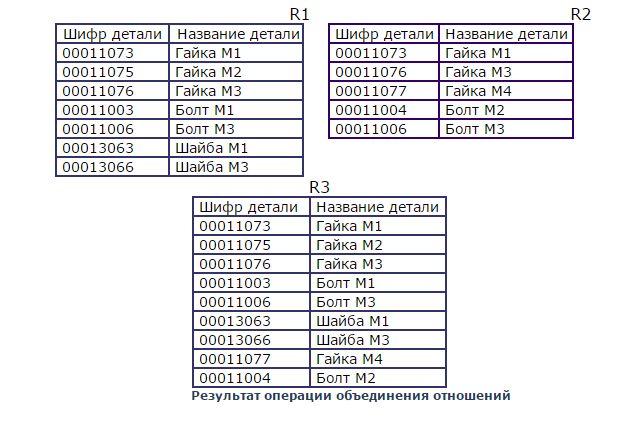
Пересечением отношений R1 и R2 называется отношение, которое содержит множество кортежей, принадлежащих одновременно и первому и второму отношениям R1 и R2: 

.

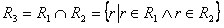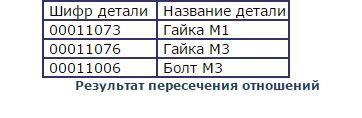
Здесь знак Λ соответствует логической операции «И» и требует одновременного выполнения исходных условий, которые он соединяет. Если мы вернемся к нашему примеру, то по смыслу операция пересечения позволит определить те изделия, которые производятся в обоих филиалах фирмы (рис. 2.7). Что нам это дает? Если таких изделий много, значит, мы можем утверждать, что наши филиалы не специализированны, т. е. в каждом филиале выпускаются почти все изделия. В противном случае, когда пересечение либо пусто, либо содержит всего пару строк, мы имеем дело с узкоспециализированными филиалами. Если нам надо просто разнести территориально наше производство чтобы удовлетворить потребности разных районов города или региона в наших изделиях, то хорошо иметь первый случай, т. е. почти полное повторение номенклатуры в обоих филиалах.

Оцените самостоятельно качественные результаты пересечения отношений для нашего примера.

Операции объединения и пересечения являются коммутативными, т. е. результат выполнения не зависит от порядка исходных отношений.

;   .

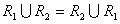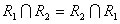Разность отношений R1 и R2 представляет собой множество всех кортежей, содержащее кортежи из R1 и не содержащее кортежи из R2: 

.

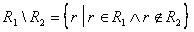Операции объединения, пересечения и разности применимы только к отношениям с эквивалентными схемами.

ВНИМАНИЕ! При выполнении теоретико-множественного объединения автоматически удаляются дубликаты кортежей!

Операция же разности является принципиально несимметричной операцией, т. е. результаты операции будут различными для разного порядка аргументов, что и видно из сравнения отношений R5 и R6. 

.

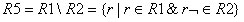Отношение R5 содержит перечень деталей, изготавливаемых только на участке 1, отношение R6 содержит перечень деталей, изготавливаемых только на участке 2 (рис. 2.8).

.

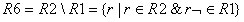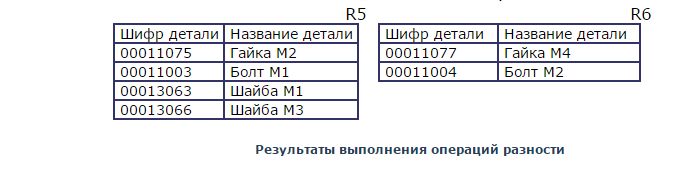
В отличие от навигационных средств манипулирования данными в теоретико-графовых моделях операции реляционной алгебры позволяют получить сразу иной качественный результат, который является семантически гораздо более ценным и понятным пользователям. Например, сравнение результатов объединения и разности номенклатуры двух участков позволит оценить специфику производства (насколько оно уникально на каждом участке) и при необходимости принять соответствующее решение по изменению номенклатуры.

Для демонстрации возможностей трех первых операций реляционной алгебры рассмотрим еще один пример — уже из другой предметной области. Исходными являются три отношения R1, R2 и R3. Все они имеют эквивалентные схемы.

R1= (ФИО, Паспорт, Школа);

R2= (ФИО, Паспорт, Школа);

R3= (ФИО, Паспорт, Школа).

Рассмотрим ситуацию поступления в высшие учебные заведения, которая была характерна для периода, когда были разрешены так называемые репетиционные вступительные экзамены, которые сдавались раньше основных вступительных экзаменов в вуз. Отношение R1 содержит список абитуриентов, сдававших репетиционные экзамены. Отношение R2 содержит список абитуриентов, сдававших экзамены на общих условиях. И, наконец, отношение R3 содержит список абитуриентов, принятых в институт. Будем считать, что при неудачной сдаче репетиционных экзаменов абитуриент мог делать вторую попытку и сдавать экзамены в общем потоке, поэтому некоторые абитуриенты могут присутствовать как в первом, так и во втором отношении.

Список абитуриентов, которые поступали два раза и не поступили в вуз:

.

Список абитуриентов, которые поступили в вуз с первого раза, т. е. они сдавали экзамены только один раз и сдали их так хорошо, что сразу были зачислены в вуз:

.

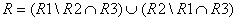Список абитуриентов, которые поступили в вуз только со второго раза. Прежде всего это те абитуриенты, которые присутствуют в отношениях R1 и R2, потому что они поступали два раза, и присутствуют в отношении R3, потому что они поступили:

R =  .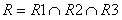

Список абитуриентов, которые поступали только один раз и не поступили. Это прежде всего те абитуриенты, которые присутствуют в R1 и не присутствуют в R2, и те, кто присутствуют в R2 и не присутствуют в R1. И, разумеется, никто из них не присутствует в R3:

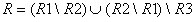
В отсутствие скобок порядок выполнения операций реляционной алгебры естественный, поэтому сначала будут выполнены операции в скобках, а затем будет выполнена последняя операция вычитания отношения R3. 

Операции объединения, пересечения и разности применимы только к отношениям с эквивалентными схемами.

Кроме перечисленных трех теоретико-множественных операций в рамках реляционной алгебры определена еще одна теоретико-множественная операция — расширенное декартово произведение. Эта операция не накладывает никаких дополнительных условий на схемы исходных отношений, поэтому операция расширенного декартова произведения, обозначаемая 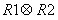 , допустима для любых двух отношений. Но прежде чем определить саму операцию, введем дополнительно понятие конкатенации, или сцепления, кортежей.

Сцеплением, или конкатенацией, кортежей c = и q = называется кортеж, полученный добавлением значений второго в конец первого. Сцепление кортежей c и q обозначается как (c, q).

(c, q) = .

Здесь n — число элементов в первом кортеже с, m — число элементов во втором кортеже q. 

Все предыдущие операции не меняли степени или арности отношений — это следует из определения эквивалентности схем отношений. Операция декартова произведения меняет степень результирующего отношения.

Расширенным декартовым произведением отношения R1 степени n со схемой

S _R1 = (A1, A2, ... , An)

и отношения R2 степени m со схемой

S _R2 = (B1, B2, ... , Bm)

называется отношение R3 степени n+m со схемой

S _R3  = (A1, A2, ... , An, B1, B2, ..., Bm),

содержащее кортежи, полученные сцеплением каждого кортежа r отношения R1 с каждым кортежем q отношения R2, т. е. если R1 = { r }, R2 = { q }

.

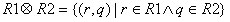Операцию декартова произведения с учетом возможности перестановки атрибутов в отношении можно считать симметричной. Очень часто операция расширенного декартова произведения используется для получения некоторого универсума, т. е. отношения, которое моделирует все возможные комбинации между элементами отдельных множеств. Однако самостоятельного значения результат выполнения операции обычно не имеет, он участвует в дальнейшей обработке.

Например, на производстве в отношении R7 задана обязательная номенклатура деталей для всех цехов, а в отношении R8 дан перечень всех цехов.

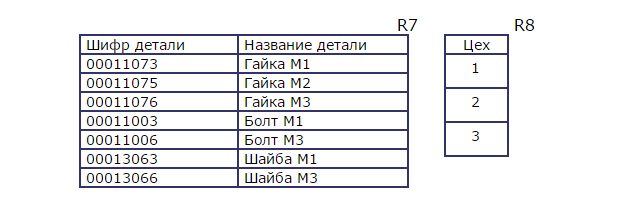
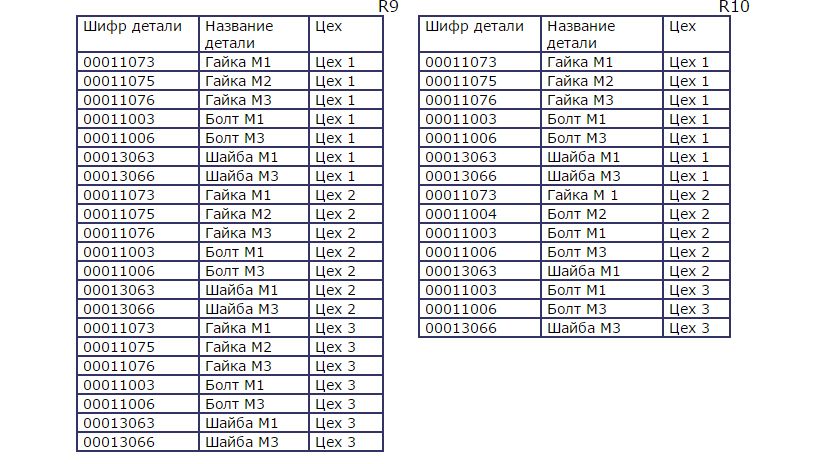
В каких запросах нужно использовать расширенное декартово произведение? Эта операция моделирует некоторую ситуацию, которая характеризуется словом «все». Поэтому если нам надо узнать, какие детали в каких цехах из общей обязательной номенклатуры не выпускаются, то мы можем вычесть из полученного отношения R9 отношение R10, характеризующее реальный выпуск деталей в каждом цехе.

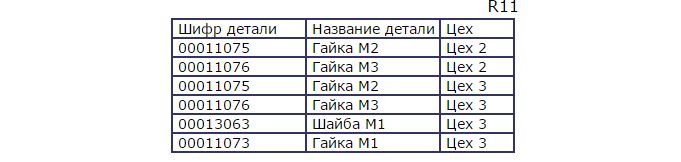
Отношение R11, которое является результатом выполнения этой операции, имеет вид:

R11 = R9 \ R10

Группа теоретико-множественных операций избыточна. Например, операцию можно заменить сочетанием операций объединения и пересечения:

.

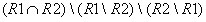Однако это достаточно сложная формула, и именно поэтому все три теоретико-множественные операции вошли в базовый набор операций реляционной алгебры.

Далее мы переходим к группе операций, названных специальными операциями реляционной алгебры.