Самостоятельная работа по геометрии в 9 классе

1 вариант

2 вариант

1.Вычислите угол α.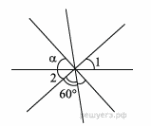

2.Найдите величину угла АОК, если ОК биссектриса угла АОD, угол DOB равен 64⁰. Ответ дайте в градусах.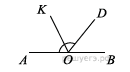

1.Вычислите угол α.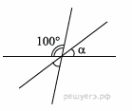

2.Найдите величину угла СМА, если MD биссектриса угла СМD, угол DМС равен 58⁰. Ответ дайте в градусах.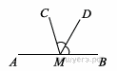

3.В треугольнике два угла равны 70⁰ и 44⁰. Найдите его третий угол.

4.Вычислить площадь фигуры.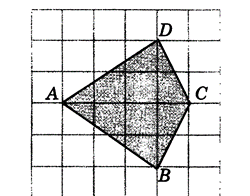

3.В треугольнике два угла равны 45⁰ и 86⁰. Найдите его третий угол.

4.Вычислить площадь фигуры.

5.Вычислите площадь трапеции.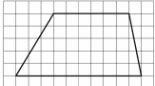

6.Найдите площади параллелограммов.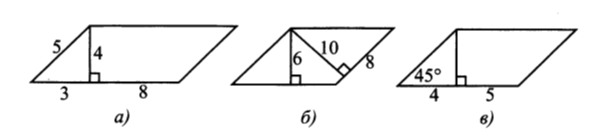

5.Вычислите площадь трапеции.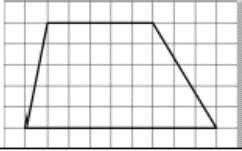

6.Найдите площади параллелограммов.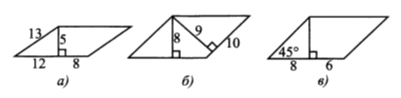

7.Укажите номера верных утверждений.

1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

2) Вертикальные углы равны.

3) Любая биссектриса равнобедренного треугольника является его медианой.

7.Укажите номера верных утверждений.

1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.

2) В любом прямоугольнике диагонали взаимно перпендикулярны.

3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.

8.Какие из следующих утверждений верны?

1) Если угол равен 45°, то вертикальный с ним угол равен 45°.

2) Любые две прямые имеют ровно одну общую точку.

3) Через любые три точки проходит ровно одна прямая.

4) Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.

8.Какие из следующих утверждений верны?

1) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.

2) Любые две прямые имеют не менее одной общей точки.

3) Через любую точку проходит более одной прямой.

4) Любые три прямые имеют не менее одной общей точки.

9.Какие из следующих утверждений верны?

1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.

2) Если угол равен 60°, то смежный с ним равен 120°.

3) Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.

4) Через любые три точки проходит не более одной прямой.

9.Какие из следующих утверждений верны?

1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.

2) Если угол равен 60°, то смежный с ним равен 120°.

3) Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.

4) Через любые три точки проходит не более одной прямой.

10.Какие из следующих утверждений верны?

1) Сумма углов выпуклого четырехугольника равна 180°.

2) Если один из углов параллелограмма равен 60°, то противоположный ему угол равен 120°.

3) Диагонали квадрата делят его углы пополам.

4) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.

10.Какие из сле­ду­ю­щих утверждений верны?

1) Если в па­рал­ле­ло­грам­ме диагонали равны, то этот параллелограмм — прямоугольник.

2) Если диа­го­на­ли параллелограмма делят его углы пополам, то этот параллелограмм — ромб.

3) Если один из углов, при­ле­жа­щих к сто­ро­не параллелограмма, равен 50°, то дру­гой угол, при­ле­жа­щий к той же стороне, равен 50°.

4) Если сумма трех углов вы­пук­ло­го четырехугольника равна 200°, то его чет­вер­тый угол равен 160°.