ШКОЛЬНЫЙ ЭТАП 2019-2020 уч. год
10 класс
(3 часа или 4 урока)
Несколько учеников отвечали на уроке, и каждый получил не ниже тройки. Аня получила отметку, которая на 10 меньше, чем сумма отметок остальных; Боря получил отметку, которая на 8 меньше, чем сумма отметок остальных; Вера – отметку, которая на 6 меньше, чем сумма отметок остальных. Сколько человек отвечало на уроке и какие отметки они получили?
Решение. Отвечали 4 человека. Один получил «5», двое – «4», один - «3». Пусть S – сумма всех полученных отметок, А – отметка Ани, Б – Бори и В – Веры. Из условия следует, что S-А=А+10; S-Б=Б+8; S-В=В+6. Значит S=2А+10=2Б+8=2В+6. Отсюда следует, что В–Б=Б-А=1. Так как двоек не было, то возможен только один вариант: А=3, Б=4, В=5. Следовательно, S=16, тогда S– (А+Б+В)=4, то есть ещё один человек получил отметку «4».
Критерии.
Приведён только ответ – 0 баллов.
Верно составлено уравнение, но дальнейших продвижений нет (или они ошибочны) – 2 балла.
Верно найдены оценки некоторых из детей, но не всех – 4 балла.
Любое полное верное решение – 7 баллов.
Сколько существует шестизначных чисел, у которых все цифры ненулевые и каждая цифра встречается ровно два раза?
Ответ: 7560 чисел.
Решение.
Подсчитаем количество таких чисел, не содержащих 0. Тогда выбрать три цифры можно 9×8×7:(3×2×1)=84 способами. Расположить 6 цифр (каждая по два раза) можно 6!=720 способами. Учитывая, что цифры одинаковые, разделим на 2×2×2=8 и получим 90 способов. Тогда всего чисел будет 84×90=7560.
Критерии.
Если дан только ответ без пояснений – 0 баллов.
Если при решении не поделили на 8 (не учтено, что две цифры неразличимы) – 3 балла.
Верное решение – 7 баллов.
На доске написано число 4321432154321. Некоторые цифры стерли так, чтобы получить наибольшее возможное число, делящееся на 9. Чему равно это наибольшее число?
Ответ. 43214321421.
Решение. Из признака делимости на 9 следует, что сумма стёртых цифр должна быть равна 8 (1). Из двух чисел больше то, в записи которого больше цифр (2). Поэтому нужно стереть две цифры – либо 4 и 4, либо 3 и 5. Из двух одиннадцатиразрядных чисел больше то, у которого в старших разрядах стоят большие цифры (3). Поэтому нужно стереть пятёрку и последнюю тройку.
Критерии.
Рассмотрены только частные случаи – 0 баллов.
Получено утверждение 1 – 2 балла.
Получено утверждение 1 и 2 – 3 балла.
В доказательстве отсутствует утверждение 3 – не более 5 баллов.
Верное решение – 7 баллов.
В трапеции ABCD с основаниями AD и BC угол при вершине A – прямой, E – точка пересечения диагоналей, F – проекция точки E на сторону AB. Докажите, что углы DFE и CFE равны.
Р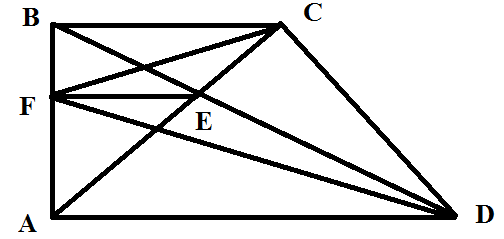 ешение. Треугольники AED и CEB подобны по двум углам (накрест лежащим, так ABCD трапеция). Тогда BE:ED=BC:AD. Так как EF перпендикулярна AB и DA перпендикулярна AB, то EF параллельна AD. Тогда по теореме Фалеса получим, что BF:FA=BE:ED. Следовательно, BF:FA=BC:AD (1). Тогда треугольники FAD и FBC подобны по двум сторонам и углу между ними.
ешение. Треугольники AED и CEB подобны по двум углам (накрест лежащим, так ABCD трапеция). Тогда BE:ED=BC:AD. Так как EF перпендикулярна AB и DA перпендикулярна AB, то EF параллельна AD. Тогда по теореме Фалеса получим, что BF:FA=BE:ED. Следовательно, BF:FA=BC:AD (1). Тогда треугольники FAD и FBC подобны по двум сторонам и углу между ними.
Значит, 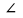 BFC=
BFC=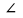 DFA. Следовательно,
DFA. Следовательно, 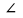 DFE=
DFE=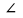 CEB.
CEB.
Критерии. Если неверное решение – 0 баллов.
Если верный ход рассуждений и получено соотношение (1) – 3 балла.
Если верное решение – 7 баллов.
На мехмате СГУ 20 раз проводился кружок по математике. На каждом занятии присутствовало ровно пять школьников, причём никакие два школьника не встречались на кружке более одного раза. Докажите, что всего на кружке побывало не менее 20 школьников.
Решение. Первый способ. Используем метод от противного. Предположим, что школьников не более 19. Тогда между ними может произойти не более чем 19×18:2=171 встреча. На каждом кружке встречается 5 школьников, то есть происходит 5×4:2=10 встреч. Тогда за 20 кружков произойдёт всего 10×20=200 встреч. Противоречие.
Второй способ. Используем метод от противного. Предположим, что школьников не более 19. Если есть школьник, который побывал на 5 занятиях, то он должен был встретить 5×4=20 других школьников. Противоречие.
Если такого школьника нет, то каждый школьник побывал не более чем на 4 занятиях. Тогда всего посещений кружков было не более 19×4=76. А должно было быть 20×5=100. Противоречие.
Критерии. Если неверное решение – 0 баллов.
Если верный ход рассуждений и есть вычислительная ошибка – 3 балла.
Если верно рассмотрен только один случай (см. второй способ) – 3 балла
Если верное решение – 7 баллов.







 ешение. Треугольники AED и CEB подобны по двум углам (накрест лежащим, так ABCD трапеция). Тогда BE:ED=BC:AD. Так как EF перпендикулярна AB и DA перпендикулярна AB, то EF параллельна AD. Тогда по теореме Фалеса получим, что BF:FA=BE:ED. Следовательно, BF:FA=BC:AD (1). Тогда треугольники FAD и FBC подобны по двум сторонам и углу между ними.
ешение. Треугольники AED и CEB подобны по двум углам (накрест лежащим, так ABCD трапеция). Тогда BE:ED=BC:AD. Так как EF перпендикулярна AB и DA перпендикулярна AB, то EF параллельна AD. Тогда по теореме Фалеса получим, что BF:FA=BE:ED. Следовательно, BF:FA=BC:AD (1). Тогда треугольники FAD и FBC подобны по двум сторонам и углу между ними. 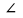 BFC=
BFC=

















