СИММЕТРИЯ В КУБЕ, ПАРАЛЛЕЛЕПИПЕДЕ, ПРИЗМЕ И ПИРАМИДЕ. ПРЕДСТАВЛЕНИЕ О ПРАВИЛЬНЫХ МНОГОГРАННИКАХ.
(Раздел «Многогранники»)
ДЕЯТЕЛЬНОСТНАЯ КАРТА УЧЕБНОГО ЗАНЯТИЯ
Профессии: 15.01.20 Слесарь по контрольно-измерительным приборам и автоматике, 09.01.03 Мастер по обработке цифровой информации, 23.01.03 Автомеханик, 09.01.01 Наладчик аппаратного и программного обеспечения
Учебные группы: КИП-21, М-21, А-21, Н-21
Учебный предмет: ООПу.04 Математика
Тема учебного занятия: Симметрия в кубе, параллелепипеде, призме и пирамиде. Представление о правильных многогранниках.
Тип урока: урок «открытия» новых знаний
Вид урока: лекция-беседа
Средства обучения:
технические: мультимедийный проектор, персональный компьютер;
информационно-коммуникационные: электронная презентация.
Цели урока:
образовательная: создание условий для овладения знаниями о симметрии в кубе, параллелепипеде, призме и пирамиде, представлением о правильных многогранниках;
развивающая: развитие умений планировать, анализировать, выдвигать гипотезы по решению заданий, применять полученные знания для выполнения упражнений;
воспитательная: воспитание интереса к изучению математики, математической культуры студентов.
Прогнозируемые результаты:
1) предметные:
сформированность знаний о симметрии в кубе, параллелепипеде, призме и пирамиде;
владение умением решать задачи вычислительного и доказательного характера с использованием знаний о симметрии и представления о правильных многогранниках;
2) метапредметные:
умение ставить перед собой цель, видеть ожидаемый результат работы;
умение объективно оценивать свои возможности, анализировать свои результаты, корректировать свои действия;
владение навыками познавательной рефлексии;
выбор оснований и критериев для сравнения;
умение структурировать полученную информацию;
умение анализировать и обобщать информацию;
умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности;
умение выражать свои мысли с достаточной полнотой и точностью.
Образовательные технологии: элементы технологии проблемного обучения; информационно-коммуникационные технологии.
Формы организации обучения: фронтальная, индивидуальная.
Методы обучения и контроля:
вербальные: беседа;
практические: метод сравнения, метод анализа и структурирования.
методы контроля и самоконтроля: устный контроль, самоконтроль.
Нормативный документ
Федеральный государственный образовательный стандарт среднего общего образования (утв. приказом Министерства образования и науки Российской Федерации (Минобрнауки России) от 17 мая 2012 г. № 413 г.). – М.: Министерство образования и науки РФ, – 2012.
Образовательные ресурсы:
Основная литература
Башмаков М. И. Математика: учебник для студ. учреждений сред. проф. образования. − М.: Издательский центр «Академия», 2018. – 256 с.
Башмаков М. И. Математика. Сборник задач профильной направленности: учеб. пособие для студ. учреждений сред. проф. образования. − М.: Издательский центр «Академия», 2014. – 416 с.
Дополнительная литература
Алимов Ш.А., Колягин Ю.М. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. Учебник. − М.: Просвещение, 2014. – 464 с.
Атанасян Л.С. Геометрия. 10 − 11 классы: учебник для общеобразовательных учреждений: базовый и профильный уровни / Атанасян Л.С., Бутузов В.Ф. и др. – М.: Просвещение, 2013. – 255 с.
Богомолов Н.В. Практические занятия по математике: Учеб. пособие для техникумов / Н.В. Богомолов. – М.: Высш. шк., 2013. – 495 с.
Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика (Книга 1): Учебное пособие. – М.: Издательство «Новая волна», 2013. – 656 с.
Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика (Книга 2): Учебное пособие. – М.: Издательство «Новая волна», 2013. – 592 с.
Никольский С.М. Алгебра и начала анализа: учебник для 10 класса общеобразоват. учреждений: базовый и профильный уровни / С.М. Никольский, М.К. Потапов. – М.: Просвещение, 2013. – 430 с.
Никольский С.М. Алгебра и начала анализа: учебник для 11 класса общеобразоват. учреждений: базовый и профильный уровни / С.М. Никольский, М.К. Потапов. – М.: Просвещение, 2013. – 464 с.
Интернет-ресурсы:
Федеральный центр информационно-образовательных ресурсов [Электронный ресурс] URL: www. fcior. edu. ru
Единая коллекции цифровых образовательных ресурсов [Электронный ресурс] URL: www. school-collection. edu. ru
Основные термины и понятия: симметрия, центр симметрии, ось симметрии, плоскость симметрии, параллелепипед, куб, тетраэдр, икосаэдр, додекаэдр, октаэдр.
ПЛАН УЧЕБНОГО ЗАНЯТИЯ
Содержание учебного материала:
1) Симметрия в кубе, параллелепипеде, призме и пирамиде.
2) Представление о правильных многогранниках.
3) Закрепление теоретического материала по теме с помощью решения задач.
Этап мотивации (самоопределения) к учебной деятельности (2 мин)
Преподаватель приветствует студентов, создает деловую обстановку, настраивает на продуктивную мыслительную деятельность.
Этап актуализации опорных знаний. Целеполагание (10 мин)
Преподаватель задает вопросы студентам:
Что такое симметрия?
Какие виды симметрии вы помните?
Студенты отвечают на эти вопросы. Преподаватель говорит о том, что сегодня они познакомятся с симметрией в многогранниках.
Формулирование темы и целей учебного занятия.
Работа над новой темой («открытие» нового знания) (34 мин)
Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Если фигура имеет центр (ось, плоскость симметрии), то говорят, что она обладает центральной (осевой, зеркальной) симметрией.
У прямоугольного параллелепипеда, как у всякого параллелепипеда, есть центр симметрии — точка пересечения его диагоналей. У него есть также три плоскости симметрии, проходящие через центр симметрии параллельно граням и три оси симметрии, проходящие через точки пересечения диагоналей противолежащих граней. Если у параллелепипеда два линейных размера равны, то у него есть еще две плоскости симметрии – плоскости диагональных сечений, а также ещё две оси симметрии.
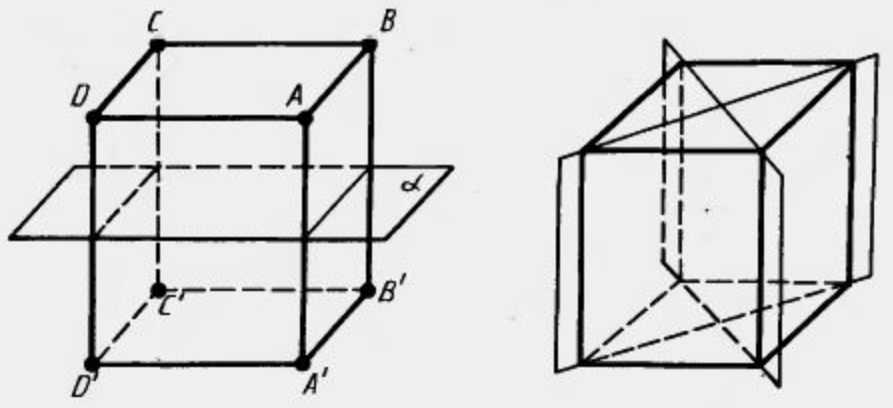
Куб имеет один центр симметрии - точку пересечения его диагоналей, девять осей и девять плоскостей симметрии.
Параллелепипед, не являющийся прямоугольным, но являющийся прямой призмой, имеет плоскость (или плоскости, если его основание - ромб), ось и центр симметрии. Параллелепипед, не являющийся прямой призмой, не имеет оси симметрии, но имеет центр симметрии и может иметь плоскость симметрии; призма и пирамида в общем случае не имеют ни плоскости, ни оси, ни центра симметрии (плоскость, ось или центр симметрии у этих многогранников могут быть лишь в некоторых частных случаях).
Правильный многогранник или платоново тело — это выпуклый многогранник с максимально возможной симметрией.
Многогранник называется правильным, если:
- он выпуклый;
- все его грани являются равными правильными многоугольниками;
- в каждой его вершине сходится одинаковое число рёбер.
икосаэдр
додекаэдр
октаэдр
куб
тетраэдр
С
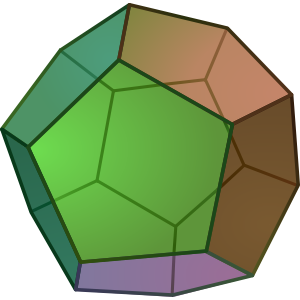
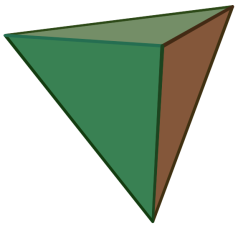
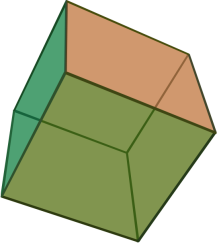
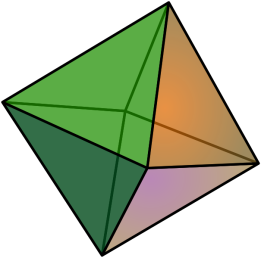
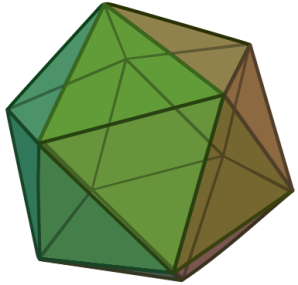
уществует всего пять правильных многогранников:
Включение нового знания в систему имеющихся знаний (38 мин)
Решение у доски и в тетрадях следующих упражнений.
Найдите угол между двумя диагоналями граней куба, имеющими общий конец.
Ребро куба равно а. Найдите площадь сечения, проходящего через диагонали двух его граней.
Докажите, что центры граней правильного октаэдра являются вер шинами куба.
Докажите, что центры граней правильного тетраэдра являются вершинами другого правильного тетраэдра.
Докажите, что центры граней куба являются вершинами правильного октаэдра.
Докажите, что сумма двугранного угла правильного тетраэдра и двугранного угла правильного октаэдра равна 180°.
Сколько плоскостей симметрии, проходящих через данную вершину, имеет правильный тетраэдр?
Рефлексия. Подведение итогов учебного занятия (5 мин)
Беседа со студентами по содержанию занятия. Вопросы для беседы:
Какая была тема сегодняшнего занятия?
Что нового вы узнали?
Какая была цель занятия?
Что получилось у вас сегодня?
Что не получилось?
Достигли ли мы поставленной цели?
6. Инструктирование о выполнении домашнего задания (1 мин)
Изучить [1] гл. 8 занятие 5
5












 уществует всего пять правильных многогранников:
уществует всего пять правильных многогранников: 









