Конспект урока в 8 классе Дата______________
Цель урока: Обобщить знания учащихся по теме дробно-рациональные уравнения
Задачи:
- повторение определения дробно-рациональные уравнения
- знание и умение применять алгоритм решения уравнений
- отработка навыков решения задач на составление дробных рациональных уравнений;
- знакомство с геометрическим способом решения уравнений;
- развитие способности к содержательному обобщению и рефлексии;
- развитие алгоритмического мышления;
- повышение интереса к решению математических задач
- показать связь с другими предметами, с жизнью.
Тип урока: Обобщения, систематизации и коррекции знаний
Оборудование: Учебник, доска, мел
Ход урока
1. Организационный момент
Приветствие. Проверка д.з. и готовности к уроку.
2. Актуализация опорных знаний.
Что называют ДРУ? Алгоритм решения?
Все задачи, решаемые с помощью дробных рациональных уравнений, можно разделить на несколько групп:
Задачи на движение по местности.
Задачи на движение по воде.
Задачи на работу.
Задачи на нахождение дробей и т.д.
Большинство задач на составление дробных рациональных уравнений в результате сводится к решению квадратных уравнений. Большой вклад в решение уравнений внес французский математик - … Как его звали? - Франсуа Виет “вызывает вас на соревнование, предлагая для решения следующие уравнения:
x2 + 8x + 15 = 0
x2 - 3x - 18 = 0
x2 - 5x + 6 = 0
x2 - 3x +2 = 0
- Как называются такие уравнения?
- Алгоритм решение задач?
I. Проверка домашнего задания с последующим использованием для углубленного изучения темы:
1) Верно ли решены уравнения?
А) 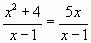 х1 =1, х2=4
х1 =1, х2=4
Ответ: нет, корень х=1 - посторонний.
Почему?
Б) 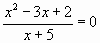 х=1
х=1
Ответ: нет, есть еще один корен Х=2.
Какой вывод нужно сделать?
2) Найти общий знаменатель дробей в каждом из уравнений:
О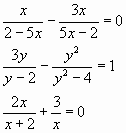 твет: 5х-2 или 2-5х
твет: 5х-2 или 2-5х
Ответ: у2-4
Ответ: х(x+2)
II. Поиск задач, математическими моделями которых являются дробные уравнения.
- Мы научились решать дробные уравнения.
А для чего они нужны? Какие задачи приводят к их появлению?
- Такие, в которых одна величина выражается через другие при помощи дробного выражения.
Например: время =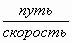 ;
; 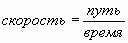 ;
;
Cторона прямоугольника=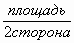 ;
;
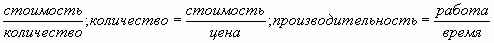 ;
;
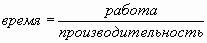 и другие.
и другие.
Итак, вы могли убедиться, что людям разных профессий приходится иметь дело с задачами на дробно-рациональные уравнения.
III. Решение задач + таблица.
Задача 1.
Поезд опаздывал на 1 час, чтобы приехать вовремя, увеличил скорость на 10 км/час на перегоне в 360 км. Найти скорость поезда по расписанию.
| | S (км) | V(км/час) | T (ч) |
| По расписанию | 360 | Х | 360 Х |
| На самом деле | 360 | Х+10 | 360 Х+10 |
360/х – 360(х+10)=1
360х+3600-360х-х2-10х=0
х 2 +10х-3600=0
Ответ:
Задача 2.
Одна мастерская должна была изготовить 420 деталей, другая, за тот же срок 500 деталей. Первая выполнила свою работу на 4 дня раньше срока, а вторая на 7. Сколько деталей в день изготовляла вторая мастерская, если известно, что ежедневно она изготовляла на 5 деталей больше, чем первая?
- О чем идет речь в задаче? (О двух мастерских)
- Значит имеем: 1 и 2 мастерские
- Чем занимались эти мастерские ?
- Что спрашивается в задаче?
Пусть х (х0)l деталей в день изготавливала П мастерская, тогда 1 изготавливала (Х-5) деталей в день. Сколько дней работала каждая мастерская?
- Какая из них быстрее справилась с работой?
- На сколько? (На 3 дня раньше чем 1 мастерская)
| | Детали | Количество деталей в день | Сколько дней работала | Справились раньше |
| 1 мастерская | 420 | (х-5) | 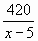
| на 4 дня |
| 2 мастерская | 500 | Х | 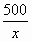
| На 7 дней |
Получим уравнение 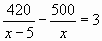
х(х-5)
Значит 2 мастерская изготавливала в день 20 деталей.
Ответ: 20 деталей.
3. Итог урока.Рефлексия
Общеизвестно высказывание: “Решение математической задачи можно сравнить со взятием крепости”. После данного урока решение большинства задач, я надеюсь, со взятием крепости уже не ассоциируется. Вы согласны со мной, ребята?
Сегодня на уроке мы
1. Повторили…
2. Узнали…
3. Закрепили…
- Какие трудности у вас возникли?
4. Домашнее задание: Подготовиться к К.Р. Придумать задачу по уравнению и решить ее 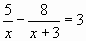







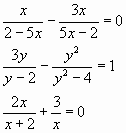 твет: 5х-2 или 2-5х
твет: 5х-2 или 2-5х 









