

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Системы линейных неравенств и решение экономических задач
Категория:
Алгебра
26.04.2019 15:26
© 2019, Иванченко Ирина Алексеевна 3645 48






 (больше), С помощью неравенств задаются основные числовые множества, формулируются определения предела, непрерывной функции, монотонной последовательности и функции, целого ряда других важных понятий. Часто то или иное неравенство служит важным вспомогательным средством, основной леммой, позволяющей доказать или опровергнуть существование каких-то объектов, оценить их количество, провести классификацию. " width="640"
(больше), С помощью неравенств задаются основные числовые множества, формулируются определения предела, непрерывной функции, монотонной последовательности и функции, целого ряда других важных понятий. Часто то или иное неравенство служит важным вспомогательным средством, основной леммой, позволяющей доказать или опровергнуть существование каких-то объектов, оценить их количество, провести классификацию. " width="640"


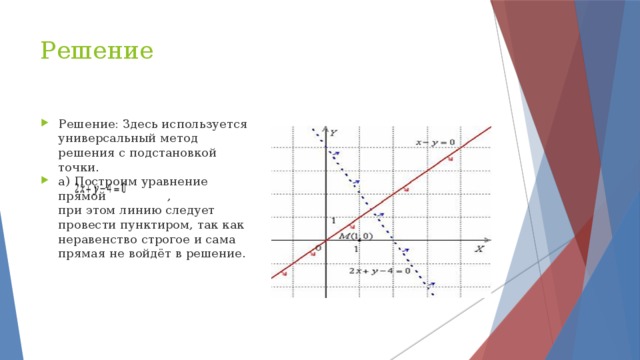
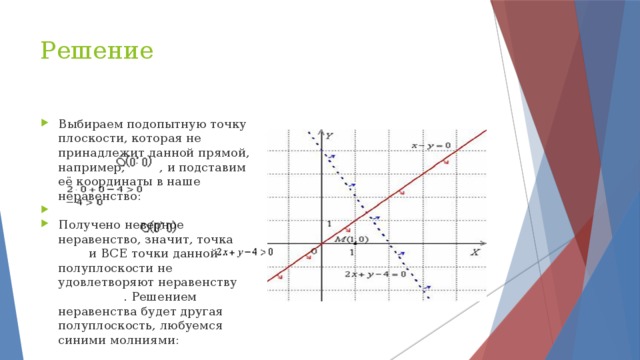
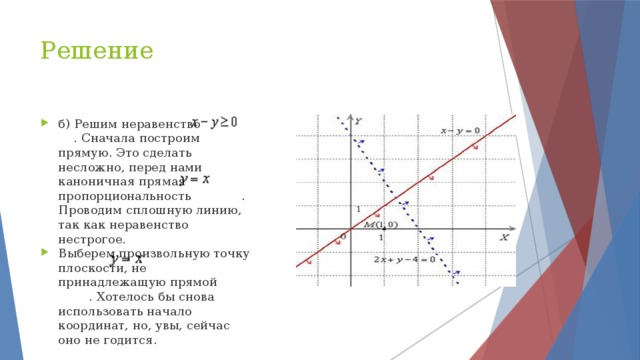
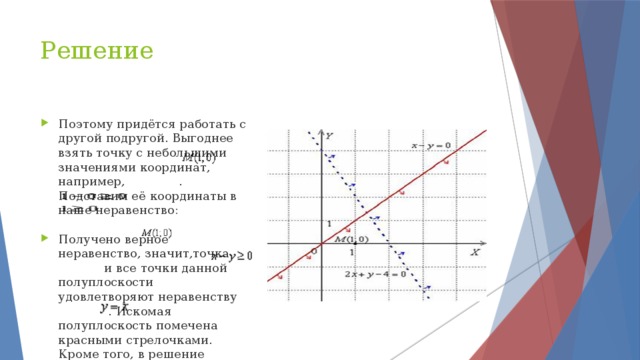


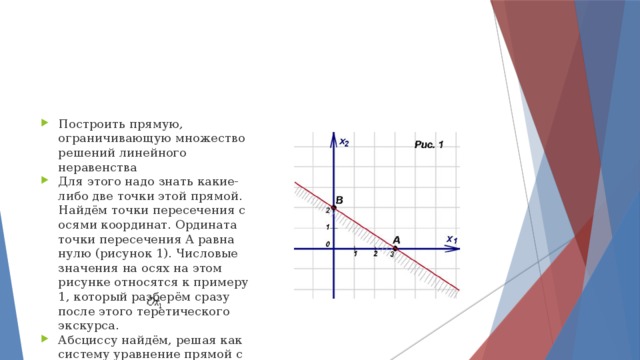
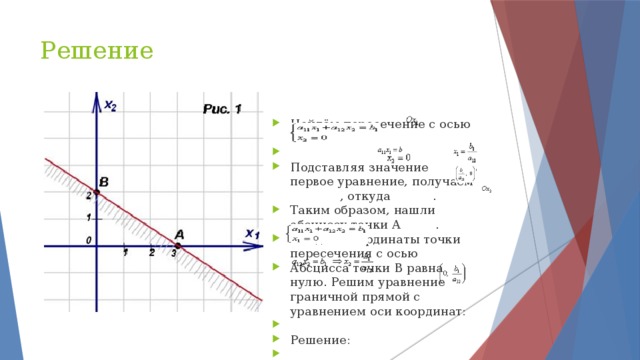










 4. Получим, что 4 Собственная скорость движения катера в стоячей воде должна быть в интервале (4; 12] км/ч. Ответ: (4; 12] км/ч. " width="640"
4. Получим, что 4 Собственная скорость движения катера в стоячей воде должна быть в интервале (4; 12] км/ч. Ответ: (4; 12] км/ч. " width="640"



















