Системы.Модели.Графы

Дата:_____________________ Урок №____ Класс: 8

Тема: «Системы, модели, графы»

Тип урока: изучение нового материала

Цель урока: получение знаний о графах, их видах, свойствах.

Задачи: сформировать у учащихся понятие «граф»; познакомить с видами графов; сформировать навыки построения графов.

УУД:

- Предметные:

обобщить и систематизировать знания о графах, их видах и свойствах;

рассмотреть типы задач, которые можно решить с использованием графов;

отработать навыки преобразования ориентированного графа в дерево;

сформировать навыки построение путей в графе, поиска кратчайшего пути;

закрепить навыки работы в среде текстового процессора Microsoft Word;

- Личностные:

Развитие логического мышления, т.е. умения анализировать, обобщать, классифицировать, составлять план при выполнении практической работы на компьютере;

Развитие познавательных умений: выделять главное, планировать работу, вести поисковую деятельность;

Критически оценивать результаты своего труда, регулировать и контролировать свои действия при работе на компьютере;

- Метапредметные: развитие у учащихся универсальных учебных действий

Регулятивные:

умения соотносить свои действия с полученными результатами.

Коммуникативные:

Умение высказывать свое мнение, правильно его формулировать, аргументировать собственную позицию при выработке общего решения в совместной деятельности;

Познавательные:

умения создавать графические информационным модели;

умения представлять, анализировать и обобщать информацию, полученную в ходе исследования;

умения делать выводы, формулировать алгоритм.

Тип урока: обобщения и систематизации знаний.

Оборудование: на доске эпиграфы, граф дорог; презентация, результаты

Ход урока.

Организационный момент.

Актуализация опорных знаний

Проверка домашнего задания: параграф 9.

Задача. Расстояние от Земли до Солнца 150 млн км. Сколько времени идет до Земли свет от Солнца, если за секунду он проходит 300 тыс. км? Сколько времени понадобилось бы ракете, чтобы преодолеть такое же расстояние, если ее скорость 15 км/с?

Решение: 1)150.000.000: 300.000 = 500(сек) - луч солнца (8 мин.20 сек.)
2)150.000.000: 15 = 10.000.000(сек) – ракета

Изучение нового материала

(Слайд 1) Сегодня мы рассмотрим новую тему «Системы, модели, графы».

(Слайд 2) Мы будем употреблять термин система для обозначения сложных объектов.

Система – это объект, состоящий из взаимосвязанных элементов и существующий как единое целое (из учебника).

Граф – это средство для наглядного представления состава и структуры системы.

(Слайд 3) (Схему зарисовать в тетрадь)

Граф состоит из вершин, связанных линиями.

Направленная линия (со стрелкой) называется дугой.

Линия ненаправленная (без стрелки) называется ребром.

Линия, выходящая из некоторой вершины и входящая в неё же, называется петлей.

(Слайд 4) Рассмотрим граф на стр. 63. Здесь вершинами будут являться названия населенных пунктов.

Разберемся, почему граф на рис. 2.9 содержит ненаправленные линии (рёбра). Всякая связь имеет определенный смысл, ее можно как-то назвать. На нашем графе связи называются: «соединены дорогой». Понятно, что если поселок А соединен дорогой с поселком Б, то, значит, и Б соединен с А. Здесь не может быть односторонней связи. Такие связи называются симметричными.

(Слайд 5) А теперь рассмотрим пример системы с несимметричными связями. Изобразим в форме графа систему, состоящую из двух человек: отца (его зовут Лев) и сына (Андрей):

Стрелка (дуга) отражает связь «быть отцом». В таком случае ясно, что справедлив факт «Лев является отцом Андрея», но не наоборот. Этот факт и представлен на графе.

(Слайд 6) Граф, в котором все связи изображены дугами, называется ориентированным графом.

На рисунке 2.11 изображен ориентированный граф, содержащий информацию о мужском составе некоторой семьи.

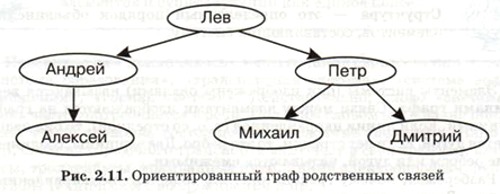
Здесь дуги обозначают связь «быть отцом», т. е. Лев является отцом Андрея и Петра, Андрей — отец Алексея, а Петр — отец Михаила и Дмитрия. У каждого человека может быть только один отец, но несколько детей. Поэтому в каждую вершину графа может входить только одна стрелка (дуга), а выходить — несколько. Такой граф представляет собой генеалогическое дерево.

Вершина «Лев» является корнем. От корня идут ветви, по которым можно добраться до любой другой вершины дерева только по одному пути. Конечные вершины каждой ветви называются листьями. 

(Слайд 7) Генеалогическое дерево Романовых.

(Слайд 8,9) Неориентированный граф и взвешенный граф.

(Слайд 10) Название «дерево» выбрано не случайно, потому что очевидно некоторое внешнее сходство с деревом-растением. Правда, дерево-граф выглядит перевернутым, но это связано с нашей привычкой писать сверху вниз, а не наоборот. А строить дерево удобно, начиная с корня.

Система, информационная модель которой представляется в виде дерева, называется иерархической системой.

На слайде мы видим иерархическую структуру, между частями которых установлены отношения подчиненности (директор – заместитель директора – учителя – ученики).

(Слайд 11) Рассмотрим «географическое дерево». Его корнем является вершина «Планета Земля», листьями — города.

Вершины дерева четко разделены на пять уровней.

Для дерева выполняется правило: вершины верхнего уровня связаны с вершинами нижнего уровня как «один ко многим». Один континент содержит множество стран, одна страна — множество регионов, а не наоборот.

(Слайд 12) Рассмотрим граф, имеющую структуру типа «сеть»

Здесь имеются два уровня вершин, но правило «один ко многим» не выполняется. Один ученик может посещать множество факультативов; один факультатив посещает множество учеников. Такой принцип связи называют «многие ко многим». Граф с такой структурой носит название сеть.

Элементы сети не всегда делятся по уровням. В сети возможно произвольное соединение элементов: каждый элемент может быть соединен с любым другим.

Закрепление изученного материала (15 мин).

Нарисуйте в виде графа систему, состоящую из четырех одноклассников, между которыми существуют следующие связи (взаимоотношения) — дружат: Саша и Маша, Саша и Даша, Маша и Гриша, Гриша и Саша.

Глядя на полученный граф, ответьте на вопрос: с кем Саша может поделиться секретом, не рискуя, что он станет известен кому-то другому?

Ответ:

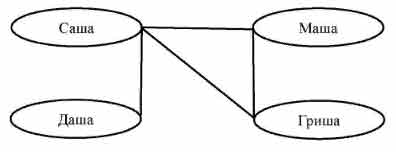
Саша может поделиться секретом с Дашей, не рискуя, что он станет известен кому-то другому.

Постройте граф структуры управления вашей школой. Оказался ли он деревом? Если да, то, что находится в корне этого дерева? Что является листьями?

Ответ: сначала директор-это корень дерева, от него стрелочки к завучам от них к учителям и от учителей к ученикам (ученики-листья)

Домашнее задание: прочитать §2.1 стр.67-68 вопросы №2,6, 10.

Домашнее задание по теме: «Системы, модели, графы»