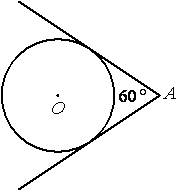Смотрите запись вебинара для учителей о современных инструментах, повышающих эффективность обучения в классе и дистанционно

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до 13.05.2025

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Была в сети 28.08.2020 15:09

Миновщикова Татьяна Евгеньевна

учитель математики

56 лет

949

60 185

Подписчики

Подписки

Местоположение

Россия, Комсомольск-на-Амуре

Специализация

Математика

Обо мне Блог Файлы Тесты Галерея Активность Награды

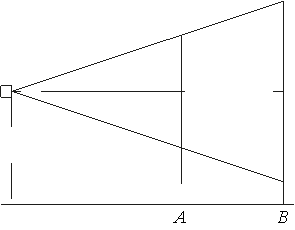
Система подготовки к ОГЭ по геометрии

Категория: Математика

04.08.2016 03:59

В данной разработке собраны задачи из открытого банка задач ФИПИ по темам: задачи 7 класса, четырёхугольники, площадь, окружность, подобие и применение подобия к решению задач.

Просмотр содержимого документа
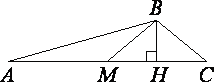
«7 кл»

	В треугольнике ABC известно, что BM — медиана и BH — высота. Известно, что AC=84 и BC=BM. Найдите AH.		Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=64°. Ответ дайте в градусах.
	На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.		В треугольнике ABC известно, что AB=BC, ∠ABC=104°. Найдите угол BCA. Ответ дайте в градусах.
	В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.		В треугольнике ABC известно, что BM — медиана и BH — высота. Известно, что AC=216, HC=54 и ∠ACB=40°. Найдите угол AMB. Ответ дайте в градусах.
	Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=19° и ∠ACB=160°. Найдите угол DCB. Ответ дайте в градусах.		В треугольнике ABC известно, что AC=BC. Внешний угол при вершине B равен 154°. Найдите угол C. Ответ дайте в градусах
	На прямой AB взята точка M. Луч MD — биссектриса угла CMB. Известно, что ∠DMC=67°. Найдите угол CMA. Ответ дайте в градусах.		Прямые m и n параллельны. Найдите ∠3, если ∠1=22°, ∠2=72°. Ответ дайте в градусах.

Просмотр содержимого документа
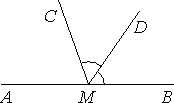
«верно-неверно»

Какое из следующих утверждений верно?

1 вариант

1)Площадь квадрата равна произведению двух его смежных сторон.

2)Диагональ трапеции делит её на два равных треугольника.

3)Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.

4)Все углы ромба равны.

5)Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.

6)Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.

7)В тупоугольном треугольнике все углы тупые.

8)В любом параллелограмме диагонали точкой пересечения делятся пополам.

9)Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.

10)Один из двух смежных углов острый, а другой тупой.

11)Площадь квадрата равна произведению двух его смежных сторон.

12)Все хорды одной окружности равны между собой.

13)Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу. 14)Площадь трапеции равна произведению основания трапеции на высоту.

15)Треугольника со сторонами 1, 2, 4 не существует.

2 вариант

16)Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.

17)Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

18)Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.

19)Площадь треугольника меньше произведения двух его сторон.

20)Средняя линия трапеции равна сумме её оснований.

21)Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

22)любой квадрат является ромбом.

23)Против равных сторон треугольника лежат равные углы.

24)Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.

25)Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.

26)В любой четырёхугольник можно вписать окружность.

27)Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.

28)Через две различные точки на плоскости проходит единственная прямая.

29)В любом прямоугольнике диагонали взаимно перпендикулярны.

30)У равностороннего треугольника три оси симметрии.

Просмотр содержимого документа
«окружность»

	Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.		Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.
	В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 75°. Найдите величину угла ODC.		На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
	Точка О — центр окружности, ∠BOC=160° (см. рисунок). Найдите величину угла BAC (в градусах).		Точка О — центр окружности, ∠BOC=70° (см. рисунок). Найдите величину угла BAC (в градусах).
	Найдите угол ABC. Ответ дайте в градусах.		В треугольнике ABC известно, что AC=7, BC=24, угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.
	Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 110°.		На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=38°. Найдите угол NMB. Ответ дайте в градусах.

Просмотр содержимого документа
«площадь»

	На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.		На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
	Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.		На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
	Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры		Периметр ромба равен 156, а один из углов равен 30°. Найдите площадь ромба.
	Площадь параллелограмма ABCD равна 144. Точка E — середина стороны AD. Найдите площадь трапеции AECB.		Сторона ромба равна 17, а расстояние от центра ромба до неё равно 4. Найдите площадь ромба.
	В треугольнике со сторонами 6 и 12 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 2. Чему равна высота, проведённая ко второй стороне?		Боковая сторона равнобедренного треугольника равна 68, а основание равно 120. Найдите площадь этого треугольника.

Просмотр содержимого документа
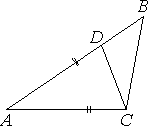
«применение подобия»

Катет и гипотенуза прямоугольного треугольника равны 10 и 26. Найдите высоту, проведённую к гипотенузе.		Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=2:3, KM=14.
	Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 21, сторона BC равна 22, сторона AC равна 28. Найдите MN.		В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 35. Найдите площадь четырёхугольника ABMN.
	Основания трапеции равны 8 и 18. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.		На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
	На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?		Проектор полностью освещает экран A высотой 50 см, расположенный на расстоянии 190 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 380 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными
	В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.		Человек ростом 1,5 м стоит на расстоянии 6 м от столба, на котором висит фонарь на высоте 10,5 м. Найдите длину тени человека в метрах.

Просмотр содержимого документа
«теория 7 класс»

ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ МАТЕРИАЛА ПО ГЕОМЕТРИИ 7 КЛАСС

Определение и свойство смежных углов (с 22)
Определение и свойство вертикальных углов (с 22)
Определение перпендикулярных прямых (с 22)
Определение биссектрисы угла (с 12)
Определение медианы (с 33)
Определение высоты (с 34)
Признаки равенства треугольников (с 30, 38, 39)
Определение равнобедренного треугольника и его свойства (с 34, 35)
Признак равнобедренного треугольника (с 73)
Определение параллельных прямых. Признаки параллельности прямых (с 54- 57)
Аксиома параллельных прямых (с 62)
Свойства параллельных прямых (с 62)
Свойства углов, образованных двумя параллельными прямыми и секущей (с 63, 65)
Сумма углов треугольника (с 75)
Определение внешнего угла и его свойство (с 70, 71)
Неравенство треугольника (с 74)
Определение прямоугольного треугольника (с 71)
Свойства прямоугольного треугольника (с 76,77)
Признаки равенства прямоугольных треугольников (с 77, 78)

Просмотр содержимого документа
«теория окружность»

ПОВТОРЕНИЕ ТЕМЫ «ОКРУЖНОСТЬ»

Определение окружности (с 43)
Определение касательной к окружности (с 166)
Свойство касательной (с 166)
Свойство отрезков касательной (с 167)
Определение центрального угла (с 170)
Как измеряется центральный угол (с 170)
Определение вписанного угла (с 171)
Как измеряется вписанный угол (с 171)
Свойства вписанного угла (с 172)
Свойство хорд окружности (с 173)
Связь касательной и секущей (с 175)
Определение вписанной окружности (с 181)
Где лежит центр вписанной окружности (с 182)
Определение описанной окружности (с 183)
Где лежит центр описанной окружности (с 184)
В какой четырехугольник можно вписать окружность (с 183)
Около какого четырехугольника можно описать окружность (с 185)

Просмотр содержимого документа
«теория подобие, решение треугольников»

ПОВТОРЕНИЕ ТЕМЫ

«ПОДОБИЕ ФИГУР И ПРИМЕНЕНИЕ ПОДОБИЯ К РЕШЕНИЮ ЗАДАЧ»

Какие треугольники называются подобными (с 139)
Что такое коэффициент подобия (с 139)
Отношение площадей подобных треугольников (с 139)
Признаки подобия (с 142, 143)
Определение средней линии треугольника и ее свойство (с 146)
Теорема Пифагора (с 131)
Теорема, обратная теореме Пифагора (с 132)
Определение синуса, косинуса, тангенса (с 156)
Свойство медиан треугольника (с 146, )
Среднее пропорциональное в прямоугольном треугольнике (с 148)
Теорема синусов (с 256)
Теорема косинусов (с 257)

Просмотр содержимого документа
«теория четырехугольники и их площадь»

ПОВТОРЕНИЕ ТЕМЫ ЧЕТЫРЕХУГОЛЬНИКИ И ПЛОЩАДИ

Сумма углов четырёхугольника (с 100)
Что такое параллелограмм (с 101)
Свойства параллелограмма (с 101)
Признаки параллелограмма (с 102, 103)
Что такое трапеция, равнобедренная трапеция (с 103)
Свойства равнобедренной трапеции (с 106)
Теорема Фалеса (с 105)
Средняя линия трапеции и её свойства (с 101)
Что такое прямоугольник (с 108)
Свойство прямоугольника (с 109)
Что такое ромб (с 109)
Свойство ромба (с 109)
Площадь квадрата (с 119)
Площадь прямоугольника (с 122)
Площадь параллелограмма (с 124, 261)
Площадь треугольника (с 125, 256)
Площадь трапеции (с 127)
Площадь ромба (с 129)
Площадь равностороннего треугольника (с 132)

Просмотр содержимого документа
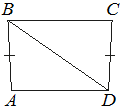
«четырехугольники»

	Диагональ прямоугольника образует угол 44° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.		Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
	В трапеции ABCD известно, что AB=CD, ∠BDA=35° и ∠BDC=58°. Найдите угол ABD. Ответ дайте в градусах.		Сторона ромба равна 10, а расстояние от точки пересечения диагоналей ромба до неё равно 3. Найдите площадь этого ромба
	Найдите площадь ромба, если его диагонали равны 19 и 6		Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 62° и 9° соответственно. Ответ дайте в градусах.
	Периметр ромба равен 60, а один из углов равен 30°. Найдите площадь этого ромба.		Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15°. Ответ дайте в градусах.
	Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 10 и 11. Найдите длину основания BC.		Основания трапеции равны 1 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.