научно-практическая конференция
«Молодые умы – науке Красноярска»
«Цепные дроби и их приложения»
Исследовательская работа.
Автор работы:
ученица 11 Б класса
МАОУ СШ № 24
Научный руководитель:
Мустяца Елена Юрьевна,
учитель математики и информатики
высшей квалификационной категории
г. Красноярск-2021
ОГЛАВЛЕНИЕ
| Введение | 3 |
| ГЛАВА I Теория цепных дробей | 4 |
| §1 Определение цепной дроби | 5-7 |
| §2 Вычисление подходящих дробей и их приложения | 8 |
| ГЛАВА II Ход и результаты исследования | 13 |
| §1 Решение уравнений в целых числах, различными методами | 13-16 |
| §2 Решение уравнений в целых числах, с помощью теории цепных дробей | 16-20 |
| Заключение | 21 |
| Литература | 22 |
ВВЕДЕНИЕ
Обучаясь в выпускном классе по системе ускоренного обучения, передо мной возникла проблема выбора формы сдачи экзамена по математике. Для того чтобы успешно сдать экзамен на профильном уровне необходимо решать задания не только первой, но второй его части. Я обратилась к своему учителю математики со следующим вопросом: решение каких заданий поможет мне получить высокий балл?
Оказывается, в последних задачах ЕГЭ профильного уровня встречаются задания на решение уравнений и неравенств в целых числах. Решение такого задания поможет получить дополнительные баллы. Мне было предложено рассмотреть вопрос использования теории цепных дробей для решения заданий второй части экзамена.
Исходя из вышесказанного, тема нашей исследовательской работы «Цепные дроби и их приложения».
Цель нашей работы: исследование теории цепных дробей в качестве инструмента решение задач ЕГЭ профильного уровня.
Объектом исследования являются цепные дроби.
Предметом исследования – цепные дроби, как инструмент решения уравнений в целых числах.
Гипотеза исследования: если изучить теорию цепных дробей и их приложения, то можно научиться решать уравнения в целых числах (от учебных до олимпиадных).
Для достижения цели исследования и подтверждения выдвинутой гипотезы нами были сформулированы следующие задачи исследования:
Изучить теорию цепных дробей.
Проанализировать задания второй части ЕГЭ нескольких последних лет.
Соотнести возможные способы решения уравнений в целых числах с решением через использование теории цепных дробей.
База исследования: типовые задания последнего задания части единого государственного экзамена на профильном уровне – задачи на целые числа.
Глава I
Цепные дроби были введены в 1572 году итальянским математиком Бомбелли. Современное обозначение непрерывных дробей встречается у итальянского математика Катальди в 1613 году. Величайший математик XVIII века Леонардо Эйлер первый изложил теорию цепных дробей, поставил вопрос об их использовании для решения дифференциальных уравнений, применил их к разложению функций, представлению бесконечных произведений, дал важное их обобщение.
Многие важные результаты этой теории принадлежат французскому математику Лагранжу, который нашел метод приближенного решения с помощью цепных дробей дифференциальных уравнений.
В современной математике приближенное представление функций обычно разыскивается в виде многочленов от независимых переменных. В тех же случаях, когда нахождение таких многочленов затруднительно, обычно применяются различные численные методы.
При этом сравнительно редко пользуются приближениями, являющимися дробно - рациональными функциями от независимых переменных.
Между тем дробно - рациональные приближения иногда могут успешно заменять данную функцию в тех областях изменения аргумента, где разложение этой функции в степенной ряд расходится и где, следовательно, приближение в виде многочленов в большинстве случаев неприменимы.
Существуют методы, позволяющие получать сколь угодно много дробно - рациональных приближений данной функции и требующие сложных выкладок. Наиболее распространенным из таких методов является метод цепных дробей.
В последнее время вырос интерес к цепным дробям в связи с их большим теоретическим и практическим значениями.
Так например, цепные дроби являются одним из аппаратов приближения функций. Они обладают замечательным свойством малого накопления погрешности при их вычислении.
В настоящее время повышение интереса к теории цепных дробей объясняется еще и тем, что, несмотря на видимую громоздкость представления, процесс их вычислений является цикличным и легко поддаётся программированию при использовании ЭВМ.
§1. Определение цепной дроби.
Цепной дробью называется выражение вида:

Такое выражение называется правильной (конечной) цепной или правильной непрерывной дробью, при этом предполагается, что  – целое число, а
– целое число, а  , …,
, …, 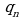 - натуральные числа.
- натуральные числа.
Где числа q1, q2, q3, q4, …, 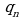 называются элементами цепной дроби.
называются элементами цепной дроби.
Цепную дробь можно так же записать:
[q1, q2, q3… qn]
Что на много упрощает запись.
Алгоритм Евклида дает возможность найти представление (или разложение) любого рационального числа в виде цепной дроби. В качестве элементов цепной дроби получаются неполные частные последовательных делений в системе равенств (1), поэтому элементы цепной дроби называются также неполными частными. Кроме того, равенства системы (2) показывают, что процесс разложения в цепную дробь состоит в последовательном выделении целой части и перевертывании дробной части.
Последняя точка зрения является более общей по сравнению с первой, так как она применима к разложению в непрерывную дробь не только рационального, но и любого действительного числа.
Разложение рационального числа  имеет, очевидно, конечное число элементов, так как алгоритм Евклида последовательного деления a на b является конечным.
имеет, очевидно, конечное число элементов, так как алгоритм Евклида последовательного деления a на b является конечным.
Понятно, что каждая цепная дробь представляет определенное рациональное число, то есть равна определенному рациональному числу. Но возникает вопрос, не имеются ли различные представления одного и того же рационального числа цепной дробью? Оказывается, что не имеются, если потребовать, чтобы было  .
.
Теорема. Существует одна и только одна конечная цепная дробь, равная данному рациональному числу, но при условии, что  .
.
Доказательство: 1) Заметим, что при отказе от указанного условия единственность представления отпадает. В самом деле, при  :
:

так что представление можно удлинить:

например, (2, 3, 1, 4, 2)=(2, 3, 1, 4, 1, 1).
2) Принимая условие  , можно утверждать, что целая часть цепной дроби
, можно утверждать, что целая часть цепной дроби  равна ее первому неполному частному
равна ее первому неполному частному  . В самом деле:
. В самом деле:
если n=1, то
если n=2, то  ; поэтому
; поэтому 
если n2, то
 =
=

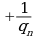 ,
,
где  1, т.к.
1, т.к. 

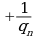
Поэтому и здесь 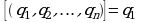 . Докажем то, что рациональное число
. Докажем то, что рациональное число  однозначно представляется цепной дробью
однозначно представляется цепной дробью  , если
, если  .
.
Пусть 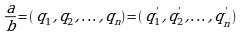 с условием
с условием  ,
, 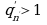 . Тогда
. Тогда  , так что
, так что 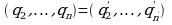 . Повторным сравнением целых частей получаем
. Повторным сравнением целых частей получаем 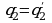 , а, следовательно,
, а, следовательно, 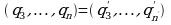 и так далее. Если
и так далее. Если  , то в продолжении указанного процесса получим также
, то в продолжении указанного процесса получим также  . Если же
. Если же  , например
, например  , то получим
, то получим  , что невозможно.
, что невозможно.
Теорема доказана.
Замечания:
В случае разложения правильной положительной дроби первый элемент  , например,
, например, 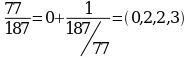 .
.
При разложении отрицательной дроби (отрицательный знак дроби всегда относится к числителю) первый элемент будет отрицательным, остальные положительными, так как целая часть отрицательной дроби является целым отрицательным числом, а ее дробная часть, как всегда, положительна.
Пример:  , а так как
, а так как  , то
, то  .
.
Всякое целое число можно рассматривать как непрерывную дробь, состоящую из одного элемента.
Пример: 5=(5);  .
.
Приведу несколько примеров разложения различных дробей и иррациональных корней в цепные дроби:
Пример 1. Разложим обыкновенную дробь 105/38 в цепную.
Включаем алгоритм Евклида.
105=38*2+29
38=29*1=9
29=9*3+2
9=2*4+1
2=1*2
Неполные частные (я их специально подчеркнул) нужно аккуратно расположить подряд на этажах цепной дроби перед знаками плюс, заменяя q. Получим:

Или:[2,1,3,4,2]
Пример 2: Представим обыкновенную дробь 539/103 в цепную.
Так же при помощи алгоритма Евклида.
Решение:
539=103*5+24
103=24*4+7
24=7*3+3
7=3*2+1
3=1*3
Получим дробь:
Пример 3: Представим обыкновенную дробь 1578/685 в цепную.
Решение:
1578=685*2+208
685=208*3+61
208=61*3+25
61=25*2+11
25=11*2+3
11=3*3+2
3=2*1+1
2=1*2
Получим:

§2 Вычисление подходящих дробей.
В §1 я показал, как переводить обычные дроби и иррациональные числа в цепную дробь, но чаще необходимо решить обратную задачу и вычислить огромную многоэтажную дробь. Многие скажут, что это очень долго и проще не обращаться к цепным дробям.
На самом деле вычислять цепную дробь еще проще, чем переходить к ней, основную роль при этом играют дроби вида:
 или
или
 которые называются подходящими дробями данной непрерывной дроби или соответствующего ей числа
которые называются подходящими дробями данной непрерывной дроби или соответствующего ей числа  .
.
Заметим, что  =
= =
= . Считается, что подходящая дробь
. Считается, что подходящая дробь  имеет порядок k.
имеет порядок k.
Прежде чем приступить к вычислению подходящих дробей заметим, что  переходит в
переходит в  , если в первой заменить
, если в первой заменить  выражением
выражением  .
.
Имеем  ,
,
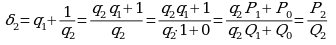 ,
,
 , …,
, …,
при этом принимается, что  ,
,  (это просто соглашение, не пугайтесь на ноль ни кто делить не собирается),
(это просто соглашение, не пугайтесь на ноль ни кто делить не собирается),  ,
,  ,
, 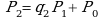 ,
,  и так далее.
и так далее.
Закономерность, которую мы замечаем в построении формулы для 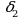 (ее числителя
(ее числителя  и знаменателя
и знаменателя 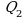 ), сохраняется при переходе к
), сохраняется при переходе к 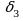 и сохранится также при переходе от k к (k+1).
и сохранится также при переходе от k к (k+1).
Поэтому, на основании принципа математической индукции, для любого k, где  , имеем
, имеем
 ;
;
причем 

Получили две формулы, которыми и будем пользоваться для вычисления цепных дробей.
Вычислять дроби очень удобно, используя таблицу.
Пример 4
Вычислим разложенную ранее в Примере 1 дробь:
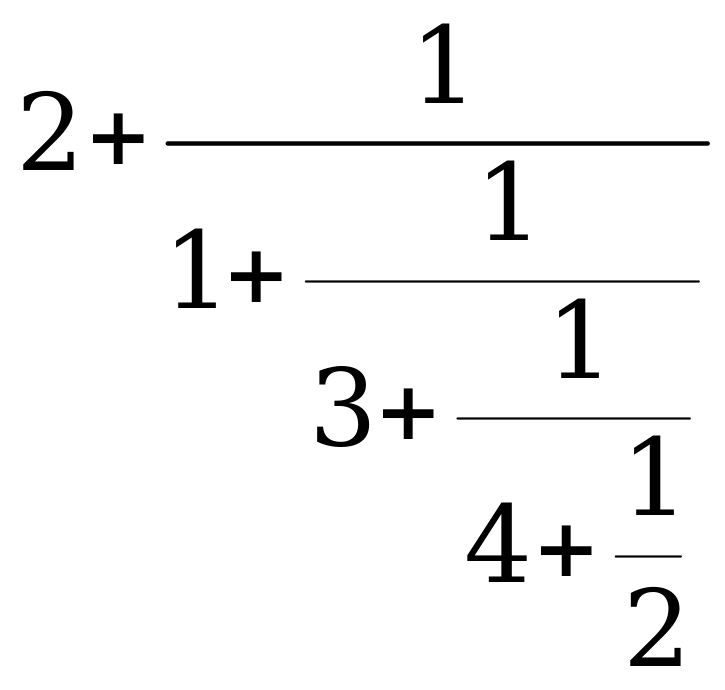
Po=1 Qo=0 P1=q1 Q1=1
P2=1*2+1=3 Q2=1*1+0=1
P3=3*3+2=11 Q3=3*1+1=4
P4=4*11+3=47 Q4=4*4+1=17
P5=2*47+11=105 Q5=2*17+4=38
Отсюда видим, что 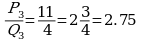 ,
,
а  - это и есть искомое число.
- это и есть искомое число.
| k | 0 | 1 | 2 | 3 | 4 | 5 |
| qk |
| 2 | 1 | 3 | 4 | 2 |
| Pk | 1 | 2 | 3 | 11 | 47 | 105 |
| Qk | 0 | 1 | 1 | 4 | 17 | 38 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 5
Вычислим разложенную ранее в Примере 3 дробь:

Очень часто необходимо сначала перевести число в цепную дробь, а потом посчитать, такие примеры у меня представлены в приложении.
С помощью цепных дробей так же решать уравнения и задачи, которые необходимо решить в целых числах.
Пример 6 (уравнение):
 142x+82y=6 /:2
142x+82y=6 /:2
Данное уравнение равносильно уравнению:
71x+41y=3
Разложим 71/41 в цепную дробь
71=41*1+30
41=30*1+11
30=11*2+8
11=8*1+3
8=3*2+2
3=2*1+1
2=1*2
Составим таблицу подходящих дробей:
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| qk |
| 1 | 1 | 2 | 1 | 2 | 1 | 2 |
| Pk | 1 | 1 | 2 | 5 | 7 | 19 | 26 | 71 |
| Qk | 0 | 1 | 1 | 3 | 4 | 11 | 15 | 41 |
На основании свойства подходящих дробей

получим:
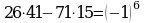 или
или 
Умножив обе части на 3 находим:

т.е. х0=-45, у0=78 – частное решение данного уравнения.
Все решения могут быть найдены по формулам:
x=-45+41t y=78-71t
где t принимает любые целые значения.
Пример 7:
Решить уравнение в целых числах:
7k-20n=5
Разложим  в цепную дробь:
в цепную дробь:

Составим таблицу подходящих дробей
| K | 0 | 1 | 2 | 3 | 4 |
| qk |
| 0 | 2 | 1 | 6 |
| Pk | 1 | 0 | 1 | 1 | 7 |
| Qk | 0 | 1 | 2 | 3 | 20 |
По свойству подходящих дробей:


Отсюда: 
Все решения могут быть найдены по формуле:
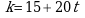

где t – все целые значения
Пример 8 (задача):
Транспортной организации, имеющей грузовые автомашины грузоподъемностью 3,5 и 4,5т, предложено перевезти 53т груза. Определим, сколько грузовых автомашин должен выделить диспетчер транспортной организации для перевозки указанного груза одним рейсом при условии полного использования грузоподъемности всех машин.
Решение:
Пусть х – число выделяемых машин грузоподъемностью 3,5т, у - число выделяемых машин грузоподъемностью 3,5т. Для получения ответа нужно решить уравнение
3,5х+4,5у=53
т.е.
35х+45у=530
в целых числах с учетом того, что 
Уравнение (1) равносильно уравнению 7х+9у=106
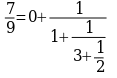
Подсчитаем подходящие дроби.
| K | 0 | 1 | 2 | 3 | 4 |
| qk |
| 0 | 1 | 3 | 2 |
| Pk | 1 | 0 | 1 | 3 | 7 |
| Qk | 0 | 1 | 1 | 4 | 9 |
По свойству подходящих дробей
 1)
1) 2)
2)
Решениями уравнения будут:

где t – любое целое число.
Теперь из всех решений выберем неотрицательные:



 и
и 

Пусть t=-47, значит Х=424+9(-47)=1 и Y=-318-7(-47)=11.
Ответ: х=1, у=11.
Глава II. Ход и результаты исследования
§1 Решение уравнений в целых числах , различными методами
Линейные уравнения в целых числах могут быть :
 Метод прямого перебора
Метод прямого перебора
 Использование неравенства
Использование неравенства
Использование отно шение делимости
шение делимости
Выделение целой части 
 Метод остатков
Метод остатков
 Метод «спуска»
Метод «спуска»
 Метод последовательного уменьшения коэффициентов по модулю
Метод последовательного уменьшения коэффициентов по модулю
 Использование формул
Использование формул

Пример№75
Решить в натуральных числах уравнения :
5х+8у=39
Метод: Использование неравенств
Решение: Для уменьшение перебора вариантов рассмотрим неравенства
 {5x=39-8y≥0 {y≤4
{5x=39-8y≥0 {y≤4
{8y=39-5x≥0 {x≤7
Проведем перебор по неизвестной у:
Если у=1, то х=6,2 не является натуральным числом.
Если у=2, то х=4,6 не является натуральным числом.
Если у=3, то х=3.
Если у=4, то х=1,4 не является натуральным числом.
Ответ: (3;3)
Пример№76
Имеются контейнеры двух видов: по 130 кг и 160 кг. Сколько было контейнеров первого и сколько второго вида, если вместе они весят 3 тонны? Укажите все решения.
Метод: Использование отношения делимости
Решение: Обозначим количество контейнеров первого вида через х, второго – через у. Получаем уравнение 130х+160у=3000 или 13х+16у=300
Далее имеем
13х+13у+3у=13*23+1,
3у-1=13(23-х-у)
Отсюда следует, что разность 3у-1 делится на 13.
Если 3у-1=0, то у не является натуральным числом.
Если 3у-1=13, то у не является натуральным числом.
Если 3у-1=26, то у=9 и х=12.
Если 3у-1=39, то у не является натуральным числом.
Если 3у-1=52, то у не является натуральным числом.
Если 3у-1=65, то у=22, но 16*22=352300.
Ответ: 12 контейнеров по 130 кг и 9 по 160 кг.
Пример№77
У осьминога 8 ног, а у морских звезды 5. Сколько в аквариуме тех и других, если всего у них 39 ног?
Метод: Выделение целой части
Решение: Пусть х- количество осьминогов, у- количество м


 орских звезд, тогда получаем уравнение 8х+5у=39
орских звезд, тогда получаем уравнение 8х+5у=39
Выразим у из уравнения и выделим целую часть:
39-8х 3х-4


 у= = 7-х .
у= = 7-х .
5 5
Отсюда следует, что разность 3х-4 делиться на 5.
Если 3х-4=0, то х не является натуральным числом.
Если 3х-4=5, то х=3 и у=3.
Если 3х-4=10, то х не является натуральным числом.
Если 3х-4=15, то х не является натуральным числом.
Если 3х-4=20, то х=8, но 8*8=6439.
Ответ: 3 и 3.
Замечание: В двух последних примерах использовано отношение делимости, при этом уравнения приводились к разному виду. В этих примерах для уменьшения перебора вариантов можно было дополнительно использовать неравенства.
Пример№78
Решить в целых числах уравнение 3х-4у=1.
Метод: Остатков
Решение: Перепишем уравнение в виде 3х=4у+1. По сколько левая часть уравнения делится на3, то должна делится на 3 и правая часть. Рассмотрим три случая.
1.Если у=3m, где m € Ƶ, то 4у+1=12m+1 не делится на3.
2.Если у=3m+1, то 4у+1=4(3m+1)+1=12m+5 не делится на3.
3.Ели у=3m+2, то 4y+1=4(3m+2)+1=12m+9 делится на 3, поэтому 3х=12m+9, х=4m+3.
Ответ: х=4m+3, у=3m+2, где m € Ƶ
Пример №79
Решить в целых числах уравнение 5х-7у=3
Метод: «Спуска»
Решение: Выразим из уравнения то неизвестное, коэффициент при котором меньше по модулю:
7х+3 2у+3

 х= = у+ .
х= = у+ .
5 5
 Дробь 2у+3 должна быть равна целому числу.
Дробь 2у+3 должна быть равна целому числу.
5
П оложим 2у+3 Z , где Z- целое число.
оложим 2у+3 Z , где Z- целое число.

 5
5
Тогда 2у+3=5z. Из последнего уравнения выразим то неизвестное, коэффициент при котором меньше по модулю, и проделаем аналогические преобразования:
5z-3 z+3

 х= = у+ .
х= = у+ .
2 2
Дробь z+2 должна быть равна целому числу.
 2
2
Обозначим z+2 = t, где t- целое число. Отсюда z=2t-3. Последовательно
 2
2
возвращаемся к неизвестным х и у:
у=3(2t-3)-t=5t-9,
х=у+z=5t-9+2t-3=7t-12/
Ответ: х=7t-12, y=5t-9, где t € Ƶ.
Пример №80
Решить в целых числах уравнения 79у-23х=1
Метод: Последовательного уменьшения коэффициентов по модулю.
Решение: Проведем деление с остатком 79=23*3+10 и перепишем исходное уравнение в виде: 23х=79у-1=69у+10у-1,
23х-69у=10у-й.
Левая часть последнего уравнения делится нацело на 23 , поэтому и правая часть должна делиться на 23. Имеем 10у-1=23t, где t € Ƶ.
Для полученного нового уравнения повторим процедуру уменьшения коэффициента. 10y=23t+1=(2*10+3)t+1;
10y-20t=3t+1; 3t+1=10u, где u € Ƶ.
Выразим х и у через n. Так как u=3n+1, то
3t=10u-1=10(3n+1)-1=30n+9;
t=10n+3
10y=23t+1=23(10n+3)+1=230n+70;
y=23n+7.
23x=79y-1=79(23n+7)-1=79*23n+552;
x=79n+24.
Ответ: х=79n+24; y=23n+7, где n € Ƶ.
§2 Решение уравнений в целых числах, с помощью теории цепных дробей
Рассмотрим примеры из предыдущего параграфа, решив их с помощью теории цепных дробей.
Пример № 75
5x+8y=39
Составим цепную дробь
1
 ) 5 0 + 1
) 5 0 + 1
8 1 + 1

 1 + 1
1 + 1
1 + 1
 2
2
2) 5=8*0+5
8=5*1+3
5=3*1+2
3=2*1+1 Составим таблицу подходящих дробей
| K | 0 | 1 | 2 | 3 | 4 |
| qk |
| 1 | 1 | 1 | 2 |
| Pk | 1 | 1 | 2 | 3 | 8 |
| Qk | 0 | 1 | 1 | 2 | 5 |
2=1*2
Из свойств подходящих дробей следует
3) 3*5-8*2= (-1)3
3*5-8*2= -1 /*(-1)
8*2+5*(-3)=1 /*39
8*78+5*(-117)=39
То есть частное решение имеет вид
xo=78 yo=-117
x=78+5t
y=-117-8t
Так как Х и У могут быть только положительные то
{78+5t≥0, {5t≥-78, t≥-15,6
{-117-8t≥0, {-8t≥117, t≤-14,625
Ответ: х=78-75=3
у=-117+120=3 где t € Ƶ
Пример №76
130x+16y=3000,
13x+16y=300,
Составим цепную дробь
1)13 0 + 1

 16 1 + 1
16 1 + 1
 4 + 1
4 + 1
 1
1
2)13=16*0+13,
16=13*1+3, Составим таблицу подходящих дробей
| K | 0 | 1 | 2 | 3 | 4 |
| qk |
| 0 | 1 | 4 | 3 |
| Pk | 1 | 0 | 1 | 4 | 13 |
| Qk | 0 | 1 | 1 | 5 | 16 |
13=3*4+1,
3+1*3.
Из свойств подходящих дробей следует
3) 4*16-13*5= (-1)4-1
4*16-13*5= -1 /* (-1)
13*5+16*(-4)=1 /*300
13*1500+16*(-1200)=300
То есть частное решение имеет вид
xo=1500 yo=-1200
x=1500+16t
y=-13t – 1200
Так как Х и У могут быть только положительные то
{1500+16t≥0, {16t≥-1500, {t≥-93,75, {x=1500+16*(-93), {x=1500-1488, {x=12,
{-13t-1200≥0, {-13t≥1200, {t≤-92(4/13), {y=-13*(-93)=1200, {y=1203-1200, {y=9.
Ответ: 12 и 9 где t € Ƶ
Пример №77
1) 8*х+5у=39, где х0 и у0
8 1


 5 = + 1
5 = + 1
1 + 1
 1 +
1 +
2
2) 8=5*1+3
5=3*1+2
3=2*1+1
2=1*2
3)
| K | 0 | 1 | 2 | 3 | 4 |
| qk |
| 1 | 1 | 1 | 2 |
| Pk | 1 | 1 | 2 | 3 | 8 |
| Qk | 0 | 1 | 1 | 2 | 5 |
P 2=q2* Р1+ Р0=1*1+1=2 Q2=q2* Q1+Q0=1*1+=1
2=q2* Р1+ Р0=1*1+1=2 Q2=q2* Q1+Q0=1*1+=1
P3=q3* Р2+ Р1=1*2+1=3 Q3=q3* Q2+Q1=1*1+1=2
P4=q4* Р3+ Р2=2*3+2=8 Q4= q4* Q3+Q2=2*2+1=5
4) 3*5-8*2=(-1) ,
3*5-8*2= -1 /(-1)
8*2+5*(-3)=1 /*39,
8*78+5*(-117)=39
= XO=78 , УO= -117
5) Решение уравнения будет:
х=78+5t

 y= -117-8t, где t c z
y= -117-8t, где t c z
{78+5t0, {5t-78, t-15,6,
{-117-8t0, {-8t117, t
t= -15
x=78-75=3
y= -117+180=3 Ответ: 3 и 3
Пример №78
1)3х-4у=1
Составим цепную дробь
3 0 + 1
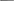
 4 1 + 1
4 1 + 1
 2+ 1
2+ 1
 1
1
2) 3=4*0+3
4=3*1+1
3=1*2+1
1=1*1 Составим таблицу подходящих дробей
| K | 0 | 1 | 2 | 3 | 4 |
| qk |
| 0 | 1 | 2 | 1 |
| Pk | 1 | 0 | 1 | 2 | 3 |
| Qk | 0 | 1 | 1 | 3 | 4 |
Из свойств подходящих дробей следует
3) 2*4-3*3=(-1)3
2*4-3*3= -1 /*(-1)
3*3-4*2=1 /1
3*3-4*2=1
То есть частное решение имеет вид
xo=3 yo=2
Ответ: x=3+4t
у=2+3t где t € Ƶ
Пример №79
5x-7y=3
Составим цепную дробь
1
 ) 5 = 0 + 1
) 5 = 0 + 1
 7 1 + 1
7 1 + 1
 2+ 1
2+ 1
2
2)5=7*0+5 Составим таблицу подходящих дробей
| K | 0 | 1 | 2 | 3 | 4 |
| qk |
| 0 | 1 | 2 | 2 |
| Pk | 1 | 0 | 1 | 2 | 5 |
| Qk | 0 | 1 | 1 | 3 | 7 |
7=5*1+2
5=2*2+1
2=1*2
Из свойств подходящих дробей следует
3) 2*7-5*3= (-1)3
2*7-5*3=-1 /*(-1)
5*3+2*(-7)= /*3
5*8-7*6=3
То есть частное решение имеет вид
xo=9 yo=6
Ответ: x=9+7t
y=6+5t где t € Ƶ
Пример №80
1)79у-23х=1
Составим цепную дробь
79 3 + 1


 23 2 + 1
23 2 + 1
3 + 1
 3
3
2)79=23*3+10
23=10*2+3
10=3*3+1
3=1*3
Составим таблицу подходящих дробей
| К | 0 | 1 | 2 | 3 | 4 |
| qk |
| 3 | 2 | 3 | 3 |
| Pk | 1 | 3 | 7 | 24 | 79 |
| Qk | 0 | 1 | 2 | 7 | 23 |

P2=q2*P1+P0=2*3+1=7 Q2=q2*Q1+ Q0=2*1+0=2
P3=q3*P2+P1=3*7+3=24 Q3=q3*Q2+ Q1=3*2+1=7
P4=q4*P3+P2=3*24+2=79 Q4=q4*Q3+ Q2=3*7+2=23
Из свойств подходящих дробей следует
3) 24*23-79*7= (-1)3
24*23-79*7= -1 /*(-1)
79*7+24*(-23)=1 /*1
79*7-23*24=1
То есть частное решение имеет вид
x0=7 y0=24
Ответ: х=7+23t
y=24+79t где t € Ƶ.
Заключение
В данной работе рассматривается очень интересное математическое понятие цепная дробь. Широкого практического применения они не получили, так как для них нет удобных правил выполнения арифметических действий, которые имеются для десятичных дробей. Но их преимуществом является в том, что их свойства не связаны ни с какой системой счисления. По этой причине цепные дроби эффективно используются в теоретических исследованиях. Изложение материала, которое представлено в данной работе, принципиально отличается от тех публикаций, с которыми работал автор, как по логике изложения, доступности, большому количеству практических задач и примеров, показывающих применение цепных дробей и оригинальность решения привычных задач.
Во второй главе, нашей исследовательской работы можно заметить насколько удобен оказался способ решения, линейных уравнений с двумя неизвестными. Для сравнения нами представлены решения этих задач различными методами, которые подразумевают, что учащийся должны обладать приличным «багажом знаний». Сравнивая рассмотренные методы с решениями через использование теории цепных дробей и свойств подходящих дробей, видно удобство и универсальность рассматриваемого способа решения.
Таким образом, цель нашего исследования достигнута частично, так как мы рассмотрели довольно узкий круг задач встречающихся в ЕГЭ по математики на профильном уровне. Однако, выдвинутая гипотеза полностью подтвердилась.
Литература
В.О. Бугаенко. Уравнения Пелля. – МЦНМО, 2002.
В.И. Арнольд. Цепные дроби. - МЦНМО, 2002.
Математическая энциклопедия, том V, М, «Советская энциклопедия», 85.
Ш.Х. Михелович. Теория чисел. М, «Высшая школа», 67.
А.А. Бухштаб. Теория чисел. М, «Просвещение», 96.
Г.Д. Балк. Математика после уроков. М, «Просвещение», 71.
А.А. Кочева. Задачник-практикум по алгебре и теории чисел. М, «Просвещение», 84.
Е.С. Ляпин, А.Е. Евсеев. Алгебра и теория чисел. М, «Просвещение», 74.
Л.Я. Куликов, А.И. Москаленко, А.А. Фомин. Сборник задач по алгебре и теории чисел. М, «Просвещение», 93.
И.М. Виноградов. Основы теории чисел. М, «Наука», 72.
Алгебра и теория чисел. Под редакцией Н.Я. Виленкина, М, «Просвещение»,
Математика ЕГЭ 2011 (типовые задания С6) . Задачи на целые числа (от учебных задач до олимпиадных) Корянов А.Г., и Прокофьев А.А.

-числители

-знаменатели
















 или
или  , …,
, …, 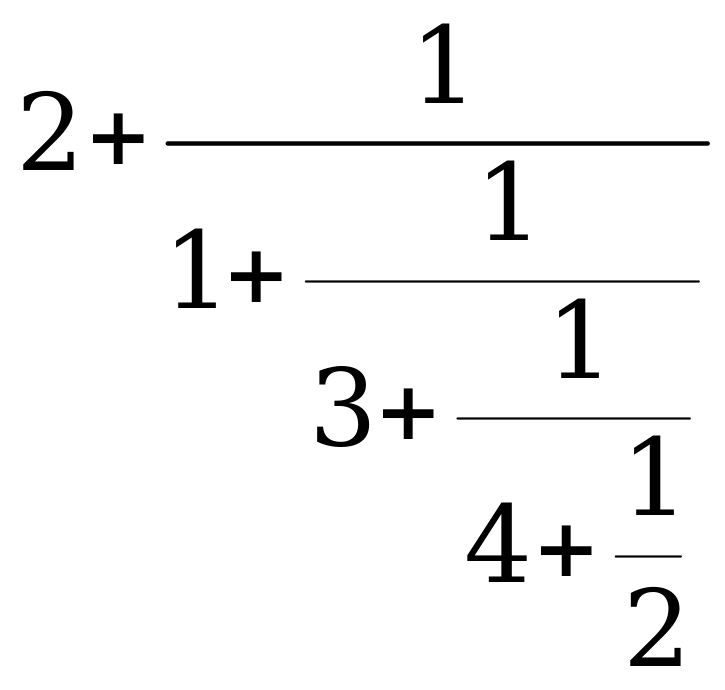


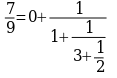

 Метод прямого перебора
Метод прямого перебора {5x=39-8y≥0 {y≤4
{5x=39-8y≥0 {y≤4


 у= = 7-х .
у= = 7-х .
 х= = у+ .
х= = у+ . Дробь 2у+3 должна быть равна целому числу.
Дробь 2у+3 должна быть равна целому числу.  оложим 2у+3 Z , где Z- целое число.
оложим 2у+3 Z , где Z- целое число.

 ) 5 0 + 1
) 5 0 + 1
 2
2
 16 1 + 1
16 1 + 1 4 + 1
4 + 1 1
1

 5 = + 1
5 = + 1 1 +
1 + 2=q2* Р1+ Р0=1*1+1=2 Q2=q2* Q1+Q0=1*1+=1
2=q2* Р1+ Р0=1*1+1=2 Q2=q2* Q1+Q0=1*1+=1
 y= -117-8t, где t c z
y= -117-8t, где t c z
 2+ 1
2+ 1 1
1
 ) 5 = 0 + 1
) 5 = 0 + 1 7 1 + 1
7 1 + 1
 23 2 + 1
23 2 + 1 3
3

















