ФЕСТИВАЛЬ ТВОРЧЕСКИХ ОТКРЫТИЙ И ИНИЦИАТИВ «ЛЕОНАРДО»
Секция «Математика»
Способы нахождения площадей фигур или задачи на клетчатой бумаге
| Выполнила: Кебина Диана Сергеевна, 6 Г класс, МБОУ «Гимназия № 9 «Гармония» г. Горно-Алтайска» Научный руководитель: Боделукова Ольга Петровна учитель математики, первой квалификационной категории, МБОУ «Гимназия № 9 «Гармония» г. Горно-Алтайска»
|
г. Горно-Алтайск,
2021 г.
ОГЛАВЛЕНИЕ
Введение..…………………………………………………………..… 3
Основная часть:
Площадь фигуры как сумма площадей её частей……………. 4
Площадь фигуры как часть площади прямоугольника……… 5
Формула Пика…………………………………………………. 6-7
Задачи с практическим содержанием………………………… 8
Задачи из государственной итоговой аттестации……………. 8
Заключение………………………………………………………….. .. 9
Список литературы и источников………………………………. …. 10
Приложение……………………………………………………… …. 11
Введение
Ещё в начальной школе мы изучали формулы нахождения площадей прямоугольника S = a ∙ b, квадрата S = a ∙ a и прямоугольного треугольника S = (a ∙ b) / 2.
При изучении математики в 5 классе мы тоже использовали эти формулы для вычисления площадей фигур. А также изучили основные свойства площадей: равные фигуры имеют равные площади; площадь фигуры равна сумме площадей её частей. В нашем учебнике встречаются задачи на клетчатой бумаге на нахождение площадей фигур. [1]
Мне стало очень интересно, какие способы решения таких задач существуют. При изучении литературы я обнаружила, что их достаточное количество. Я решила изучить их и проверить какой из них самый результативный, т.е. малозатратный по времени и дает безошибочный результат.
Проблема: Вычисление площадей сложных фигур с помощью формулы Пика легче, чем вычисление методом достраивания и разбивания фигур на части?
Цель работы: Исследование рациональности использования формулы Пика при решении задач на нахождение площади фигур, изображённых на клетчатой бумаге.
Задачи:
Изучить способы решения задач на клетчатой бумаге.
Выбрать наиболее оптимальный способ.
Объект исследования: Задачи на вычисление площади различных фигур на клетчатой бумаге.
Предмет исследования: Способы вычисления площади фигур на клетчатой бумаге.
Методы исследования: 1) теоретический: изучение литературы;
2) эмпирический: анализ, сравнение; 3) математический: построение фигур, вычисления.
Актуальность: при решении задач по математике и геометрии часто встречаются задачи, где нужно вычислить площадь фигур.
Задания на нахождение площади фигур на клетчатой бумаге встречаются в КИМах ОГЭ и ЕГЭ. А на экзамене очень важно решить задание правильно и при решении затратить как можно меньше времени.
Рассмотрим основные способы решения таких задач.
Основная часть
Площадь фигуры как сумма площадей её частей
Задача 1. Найдём площадь фигуры АВСD (рисунок 1). Если клетки размером 1х1см.
Р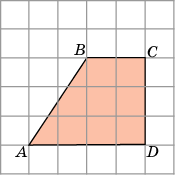 азобьем фигуру АВСD на части (1 и 2).
азобьем фигуру АВСD на части (1 и 2).
По свойству площадей:

2
S = S1 + S2 = (2∙3):2 + 3∙2
= 3 + 6 = 9 см.²
1
Ответ: 9 см.²
Рисунок 1.
Задача 2. Найдём площадь фигуры АВСD (рисунок 2). Если клетки размером 1х1см.
Р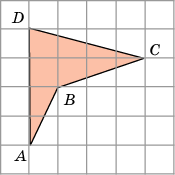 азобьем фигуру АВСD на части (1, 2, 3 и 4).
азобьем фигуру АВСD на части (1, 2, 3 и 4).
П
1
о свойству площадей:


2
3
4
S = S1 + S2 + S3 + S4 =

(1∙4):2 + (1∙3):2 + 1∙1 + (1∙2):2
= 2 + 1,5 + 1 + 1 = 5,5 см.²
Ответ: 5,5 см.²
Рисунок 2.
З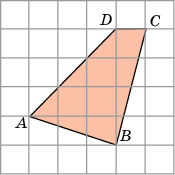 адача 3. Найдём площадь фигуры АВСD (см.рис.3). Если клетки размером 1х1см.
адача 3. Найдём площадь фигуры АВСD (см.рис.3). Если клетки размером 1х1см.
1
Разобьем фигуру АВСD на части (1, 2 и 3).
П
2
о свойству площадей:
S = S1 + S2 + S3 =
=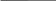
3
(1∙4):2 + (3∙3):2 + (1∙3):2
= = 2 + 4,5 + 1,5 = 8 см²
Ответ: 8 см²
Рисунок 3.
Площадь фигуры как часть площади прямоугольника
Задача 4. Найдём площадь фигуры АВСD (рисунок 4). Если клетки размером 1х1см.
О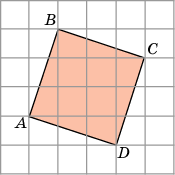 пишем около фигуры АВСD прямоугольник.
пишем около фигуры АВСD прямоугольник.
И


1
4
з площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур (1, 2, 3 и 4):
S
2
3
= Sпр – S1 – S2 – S3 – S4 =
=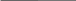 4∙4 – (3∙1):2 – (3∙1):2 – (3∙1):2 – (3∙1):2 = 16 – 1,5 – 1,5 – 1,5 – 1,5 = 10 см.²
4∙4 – (3∙1):2 – (3∙1):2 – (3∙1):2 – (3∙1):2 = 16 – 1,5 – 1,5 – 1,5 – 1,5 = 10 см.²
Рисунок 4. Ответ: 10 см.²
Задача 5. Найдём площадь фигуры АВСD (рисунок 5). Если клетки размером 1х1см.
О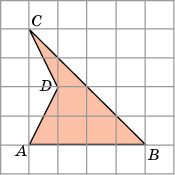 пишем около фигуры АВСD прямоугольник.
пишем около фигуры АВСD прямоугольник.
И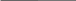



1
2
3
з площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур (1, 2 и 3):
S = Sпр – S1 – S2 – S3 =
= 4∙4 – (4∙4):2 – (2∙1):2 – (2∙1):2 = 16 – 8 – 1 – 1 =
= 6 см.²
Рисунок 5 Ответ: 6 см.²
Задача 6. Найдём площадь фигуры АВСD (рисунок 6). Если клетки размером 1х1см.
О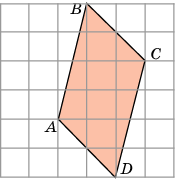



4
пишем около фигуры АВСD прямоугольник.
И
1
з площади прямоугольника вычтем площади полученных простых фигур (1, 2, 3 и 4):
S = Sпр – S1 – S2 – S3 – S4 =
=
3
3∙6 – (4∙1):2 – (2∙2):2 – (4∙1):2 – (2∙2):2
= =
2
18 – 2 – 2 – 2 – 2 = 10 см.²

Рисунок 6 Ответ: 10 см.²
Формула Пика
Л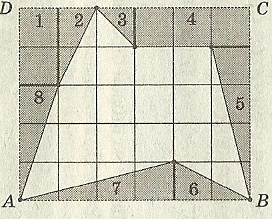 инии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки.
инии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки.
Нарисуем на листе многоугольник с вершинами в узлах (рисунок 7) и найдем его площадь. [2] Оказывается площади многоугольников, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника.
Рисунок 7.
 Пусть АВСD – прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки (рисунок 8). Обозначим через В количество узлов, лежащих внутри прямоугольника, а через Г – количество узлов на его границе. Сместим сетку на полклетки вправо и полклетки вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещённой сетки, а каждый из Г узлов – 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника
Пусть АВСD – прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки (рисунок 8). Обозначим через В количество узлов, лежащих внутри прямоугольника, а через Г – количество узлов на его границе. Сместим сетку на полклетки вправо и полклетки вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещённой сетки, а каждый из Г узлов – 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника
Рисунок 8. S = В + 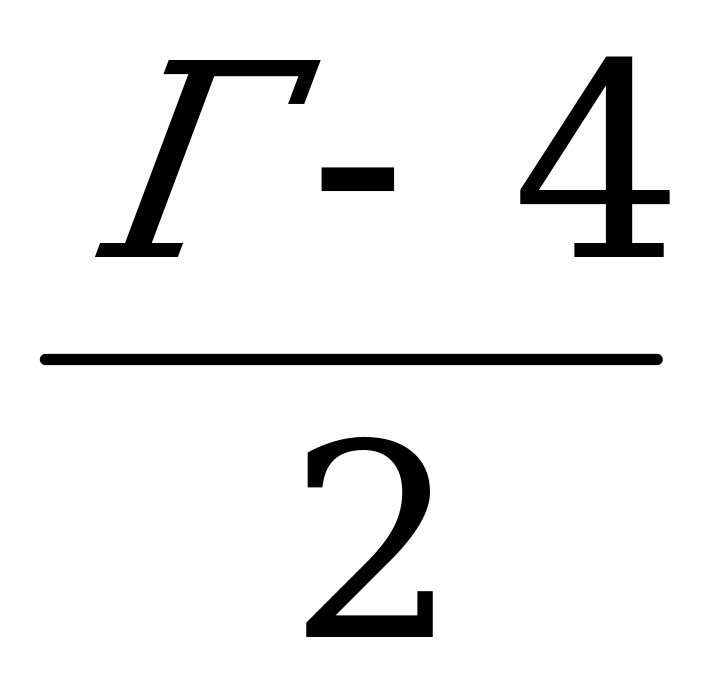 + 4 ·
+ 4 · 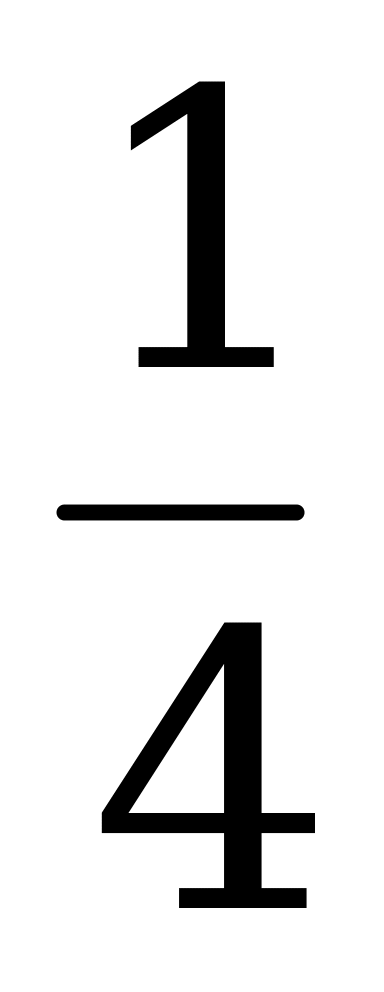 = В +
= В + 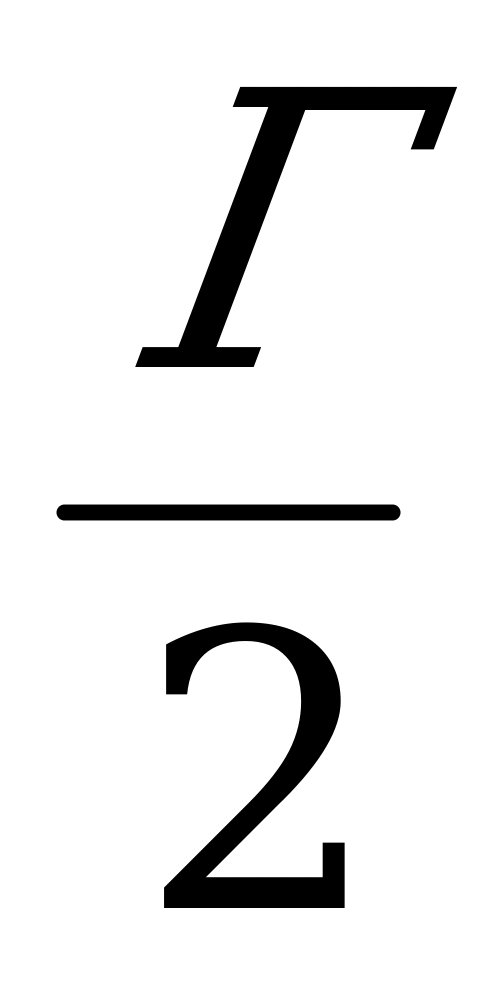 – 1.
– 1.
Для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, установлена формула S = В + 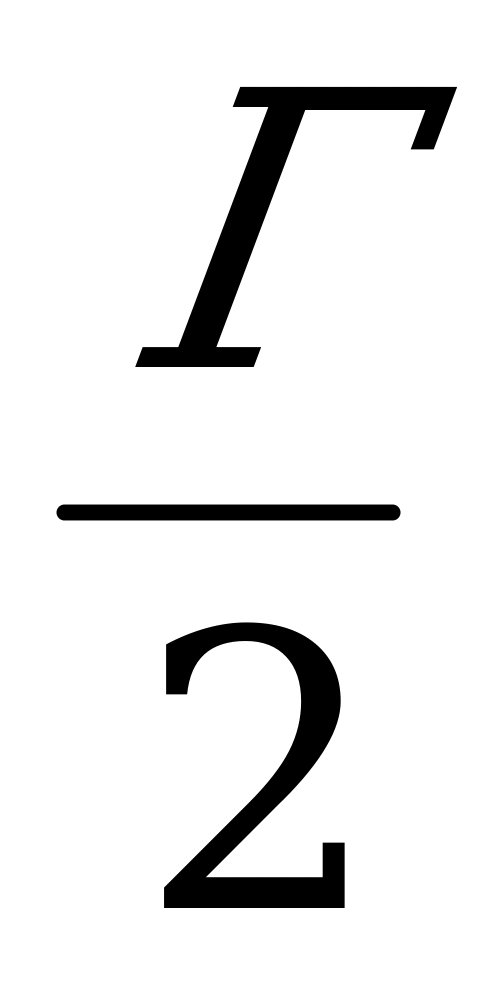 – 1. Оказывается, эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки! Это и есть формула Пика. [4]
– 1. Оказывается, эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки! Это и есть формула Пика. [4]
Она секретной не является. Информация о ней в интернете имеется. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим. Автор этой формулы австрийский математик Георг Пик (приложение 1). [8]
Можно убедиться в том, что формула Пика верна для всех рассмотренных выше примеров.
Оказывается, что если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.
Рассмотрим применение формулы Пика на примерах:
Задача 7. Найдем площадь треугольника (рисунок 9).
Отметим узлы (пересечение линий) на границе треугольника и внутри треугольника: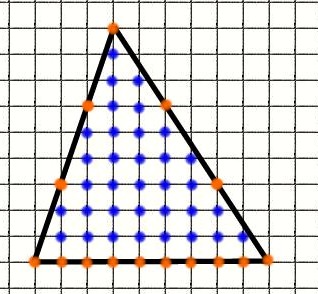
В = 34 (обозначены синим),
Г = 15 (обозначены оранжевым).
S= 34 + 15/2 – 1 = 40,5 кв.ед.
Ответ: 40,5 кв.ед
Рисунок 9.
Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо. [9]
Задача 8. Найдем площадь пятиугольника (рисунок 10).
О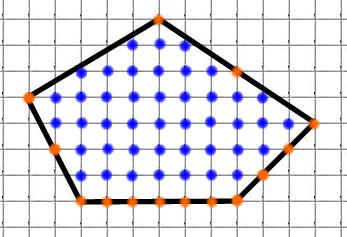 тметим узлы (пересечение линий) на границе пятиугольника и внутри пятиугольника:
тметим узлы (пересечение линий) на границе пятиугольника и внутри пятиугольника:
В = 43 (обозначены синим),
Г = 14 (обозначены оранжевым).
S= 43 + 14/2 – 1 = 49 кв.ед.
Ответ: 49 кв.ед.
Рисунок 10.
Конечно, есть ещё способы нахождения фигур на клетчатой бумаге. Например, можно просто сосчитать количество целых клеток внутри фигуры, а из оставшихся кусочков «складывать» целые клетки, но это довольно долго и трудно, особенно если фигура сложной формы.
Можно находить площади фигур на клетчатой бумаге, используя формулы площади произвольного треугольника, трапеции, ромба, параллелограмма. Но для этого нужно знать эти формулы и уметь ими пользоваться.
И есть такие фигуры на клетчатой бумаге, для которых эти формулы применить очень трудно, да и затратно по времени.
Задачи с практическим содержанием
Поможет нам формула Пика и для решения геометрических задач с практическим содержанием, когда объект изображен на клетчатой бумаге в масштабе. [4]
Задача 9. Найдите площадь лесного массива (в м²), изображённого на плане с квадратной сеткой 1 × 1см в масштабе 1 см – 200 м (рисунок 11).
Н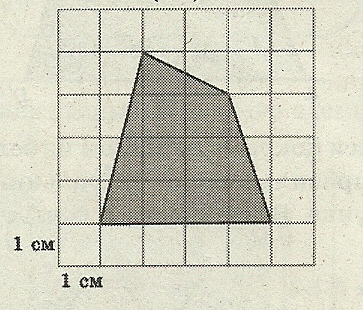 айдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S= В +
айдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S= В + 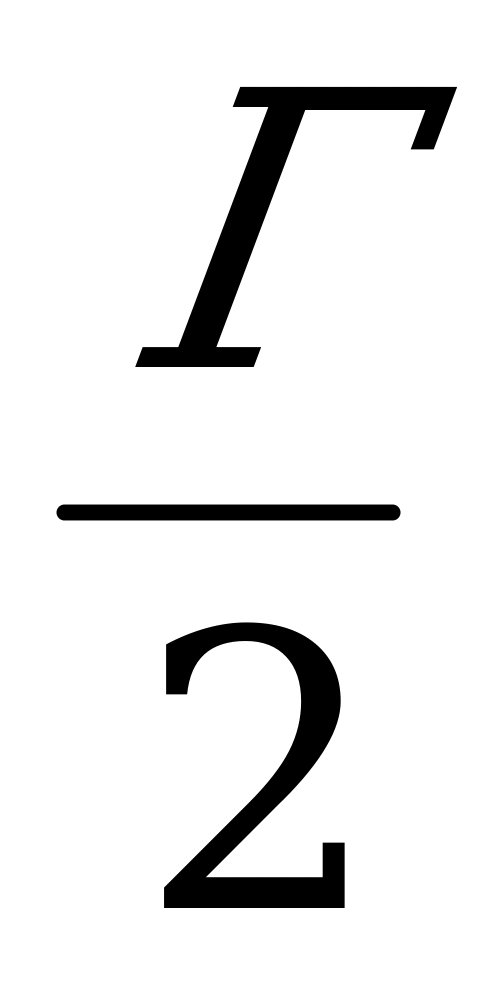 – 1
– 1
В = 8, Г = 7. S = 8 + 7/2 – 1 = 10,5 см.²
Т.к. 1 см² - 200² м.², то
Sмассива = 40000 · 10,5 = 420 000 м.²
Рисунок 11. Ответ: 420 000 м.²
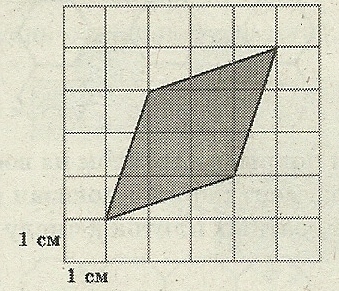 Задача 10. Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 × 1см в масштабе 1 см – 100 м (рисунок 12).
Задача 10. Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 × 1см в масштабе 1 см – 100 м (рисунок 12).
Найдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S = В + 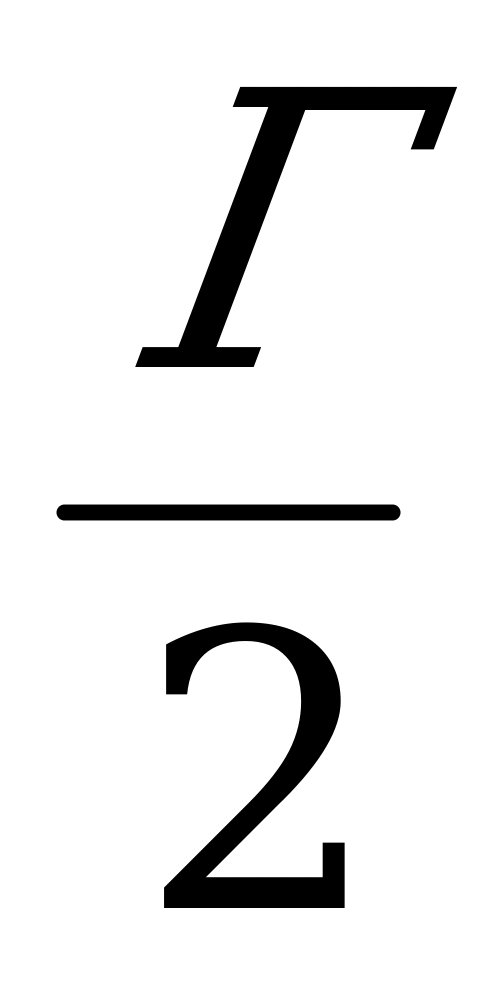 – 1. В = 7, Г = 4.
– 1. В = 7, Г = 4.
S = 7 + 4/2 – 1 = 8 см.², т.к. 1 см² - 100² м.², то
Sполя = 10000 · 8 = 80 000 м.²
Рисунок 12. Ответ: 80 000 м.²
Задачи из государственной итоговой аттестации.
Задача 11. Найти площадь фигуры (рисунок 13):
| 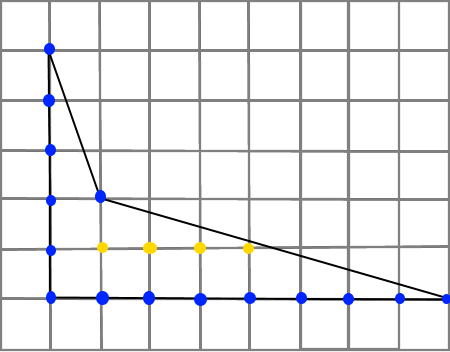
| Желтые точки – точки внутри фигуры: В = 4. Синие точки – точки на границах: Г=15. S = В + 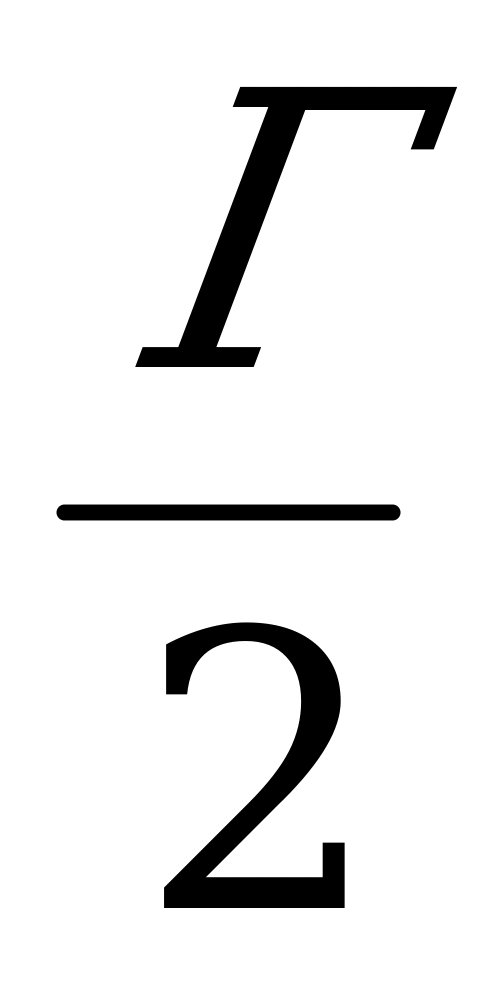 – 1 – 1 S = 4 + 15/2 – 1 = 4 + 7,5 – 1 = 10,5 кв.ед. Ответ: 10,5 кв.ед. |
Рисунок 13.
Задача 12. Найти площадь фигуры (рисунок 14):
| 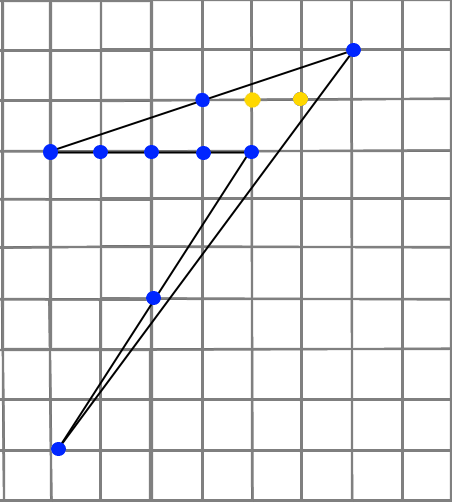
Рисунок 14. | Желтые точки – точки внутри фигуры: В=2. Синие точки – точки на границах: Г=9. S = В + 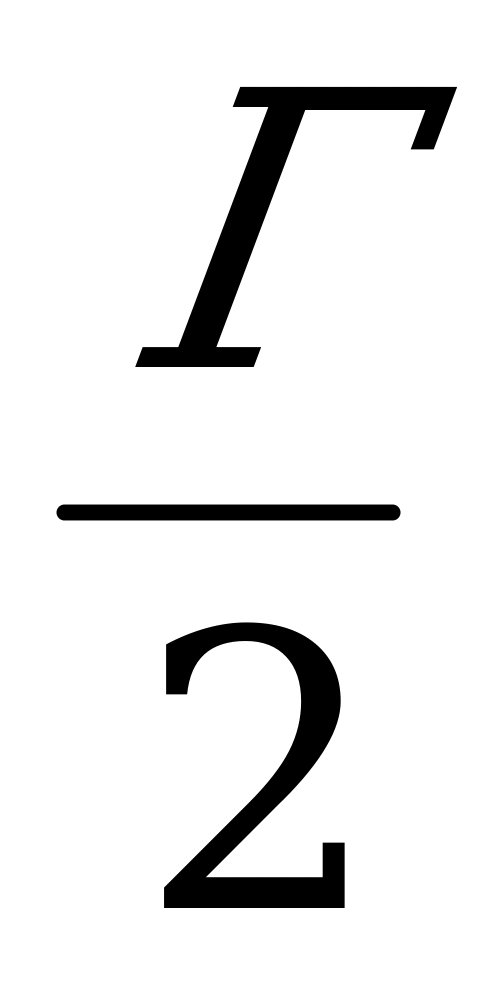 – 1 – 1 S = 2+ 9/2 – 1 = 2 + 4,5 – 1 = 5,5 кв.ед. Ответ: 5,5 кв.ед. |
Заключение
Вернемся к задаче 2.
Задача 2. Найдём площадь фигуры АВСD. Если клетки размером 1х1см.
Р азобьем фигуру АВСD на части (1, 2, 3 и 4).
азобьем фигуру АВСD на части (1, 2, 3 и 4).
П
1
о свойству площадей:


2
3
S = S1 + S2 + S3 + S4 =
=
4
(1∙4):2 + (1∙3):2 + 1∙1 + (1∙2):2 =
= 2 + 1,5 + 1 + 1 = 5,5 см.²
Ответ: 5,5 см.²
Найдем площадь по формуле Пика: В= 3; Г=7. S = В +Г/2 – 1.
S = 3+7/2 -1= 5,5 см2
Вывод: Существует достаточное количество способов нахождения площадей фигур на клетчатой бумаге. Я рассмотрела некоторые из них. Задачи, поставленные в самом начале моей работы, выполнены. Все способы нахождения площадей фигур на клетчатой бумаге хороши, но самым результативным оказался способ решения по формуле Пика!
Формула Пика имеет ряд преимуществ перед другими способами вычисления площадей многоугольников на клетчатой бумаге:
Для вычисления площади многоугольника, нужно знать всего одну формулу:
Формула Пика очень проста для запоминания.
Формула Пика очень удобна и проста в применении.
Многоугольник, площадь которого необходимо вычислить, может быть любой, даже самой причудливой формы.
Список литературы и источников
Мерзляк А.Г. Математика 5 класс. Учебник для общеобразовательных школ. – М., «Вентана-Граф», 2016.
Жарковская Н. М., Рисс Е. А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17. – [Электронный ресурс] – URL: http://mat.1september.ru/2009/23/gazeta_23_09.pdf (дата обращения 18.11.2020г.)
ФИПИ. Открытый банк заданий ЕГЭ 2020 по математике. – [Электронный ресурс] – URL: http://www.fipi.ru/content/otkrytyy-bank-zadaniy-ege (дата обращения 18.11.2020г.)
Смирнова И. М., Смирнов В. А. Геометрия на клетчатой бумаге. – М.: Чистые пруды, 2013.
Смирнова И. М., Смирнов В. А. Геометрические задачи с практическим содержанием. – М.: Чистые пруды, 2015.
Сдам ГИА. [Электронный ресурс]- URL: https://ege.sdamgia.ru/
Википедия. Формула Пика. – [Электронный ресурс] – URL: https://ru.wikipedia.org/wiki/%D4%EE%F0%EC%F3%EB%E0_%CF%E8%EA%E0 (дата обращения 18.11.2020г.)
Википедия. Пик. Георг. – [Электронный ресурс] – URL: https://ru.wikipedia.org/wiki/%D0%9F%D0%B8%D0%BA,_%D0%93%D0%B5%D0%BE%D1%80%D0%B3 (дата обращения 18.11.2020г.)
Математика? Легко!!! Площади фигур. – [Электронный ресурс] – URL: http://matematikalegko.ru/category/plocshadi-figur (дата обращения 18.11.2020г.)
Приложение
Приложение 1
Г еорг Алекса́ндр Пик (нем. Georg Alexander Pick; 10 августа 1859 г. – 13 июля 1942 г.) – австрийский математик. В 16 лет Георг окончил школу и поступил в Венский университет. В 20 лет получил право преподавать физику и математику. 16 апреля 1880 года под руководством Лео Кёнигсбергера Пик защитил докторскую диссертацию «О классе абелевых интегралов». В 1881 году он получил место ассистента у Эрнста Маха, который занял кафедру физики в Пражском университете. Чтобы получить право чтения лекций, Георгу необходимо было пройти хабилитацию. Для этого он написал работу «Об интеграции гиперэллиптических дифференциалов логарифмами». Это произошло в 1882 году, вскоре после разделения Пражского университета на чешский (Карлов университет) и немецкий (Университет Карла-Фердинанда). Пик остался в Немецком университете. В 1884 году Пик уехал в Лейпцигский университет к Феликсу Клейну. Там он познакомился с другим учеником Клейна, Давидом Гильбертом. Позже, в 1885 г., он вернулся в Прагу, где и прошла оставшаяся часть его научной карьеры. Преподавательская деятельность в Немецком университете в Праге в 1888 г. Пик получил место экстраординарного профессора математики, затем в 1892г. стал ординарным профессором. В 1910 г. Георг Пик был в комитете, созданном Немецким университетом Праги для рассмотрения вопроса о принятии Альберта Эйнштейна профессором в университет. Пик и физик Антон Лампа были главными инициаторами этого назначения, и благодаря их усилиям Эйнштейн, с которым Пик впоследствии сдружился, в 1911г. возглавил кафедру теоретической физики в Немецком университете в Праге. Круг математических интересов Пика был чрезвычайно широк. В частности, им написаны работы в области функционального анализа и дифферен-циальной геометрии, эллиптических и абелевых функций, теории дифференциальных уравнений и комплексного анализа, всего более 50 тем. С его именем связаны матрица Пика, интерполяция Пика - Неванлинны, лемма Шварца-Пика. Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники. [8]
еорг Алекса́ндр Пик (нем. Georg Alexander Pick; 10 августа 1859 г. – 13 июля 1942 г.) – австрийский математик. В 16 лет Георг окончил школу и поступил в Венский университет. В 20 лет получил право преподавать физику и математику. 16 апреля 1880 года под руководством Лео Кёнигсбергера Пик защитил докторскую диссертацию «О классе абелевых интегралов». В 1881 году он получил место ассистента у Эрнста Маха, который занял кафедру физики в Пражском университете. Чтобы получить право чтения лекций, Георгу необходимо было пройти хабилитацию. Для этого он написал работу «Об интеграции гиперэллиптических дифференциалов логарифмами». Это произошло в 1882 году, вскоре после разделения Пражского университета на чешский (Карлов университет) и немецкий (Университет Карла-Фердинанда). Пик остался в Немецком университете. В 1884 году Пик уехал в Лейпцигский университет к Феликсу Клейну. Там он познакомился с другим учеником Клейна, Давидом Гильбертом. Позже, в 1885 г., он вернулся в Прагу, где и прошла оставшаяся часть его научной карьеры. Преподавательская деятельность в Немецком университете в Праге в 1888 г. Пик получил место экстраординарного профессора математики, затем в 1892г. стал ординарным профессором. В 1910 г. Георг Пик был в комитете, созданном Немецким университетом Праги для рассмотрения вопроса о принятии Альберта Эйнштейна профессором в университет. Пик и физик Антон Лампа были главными инициаторами этого назначения, и благодаря их усилиям Эйнштейн, с которым Пик впоследствии сдружился, в 1911г. возглавил кафедру теоретической физики в Немецком университете в Праге. Круг математических интересов Пика был чрезвычайно широк. В частности, им написаны работы в области функционального анализа и дифферен-циальной геометрии, эллиптических и абелевых функций, теории дифференциальных уравнений и комплексного анализа, всего более 50 тем. С его именем связаны матрица Пика, интерполяция Пика - Неванлинны, лемма Шварца-Пика. Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники. [8]
14







 азобьем фигуру АВСD на части (1 и 2).
азобьем фигуру АВСD на части (1 и 2). 
 азобьем фигуру АВСD на части (1, 2, 3 и 4).
азобьем фигуру АВСD на части (1, 2, 3 и 4).

 (1∙4):2 + (1∙3):2 + 1∙1 + (1∙2):2 = 2 + 1,5 + 1 + 1 = 5,5 см.²
(1∙4):2 + (1∙3):2 + 1∙1 + (1∙2):2 = 2 + 1,5 + 1 + 1 = 5,5 см.²  адача 3. Найдём площадь фигуры АВСD (см.рис.3). Если клетки размером 1х1см.
адача 3. Найдём площадь фигуры АВСD (см.рис.3). Если клетки размером 1х1см.
 пишем около фигуры АВСD прямоугольник.
пишем около фигуры АВСD прямоугольник.


 4∙4 – (3∙1):2 – (3∙1):2 – (3∙1):2 – (3∙1):2 = 16 – 1,5 – 1,5 – 1,5 – 1,5 = 10 см.²
4∙4 – (3∙1):2 – (3∙1):2 – (3∙1):2 – (3∙1):2 = 16 – 1,5 – 1,5 – 1,5 – 1,5 = 10 см.² пишем около фигуры АВСD прямоугольник.
пишем около фигуры АВСD прямоугольник.






 инии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки.
инии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки.  Пусть АВСD – прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки (рисунок 8). Обозначим через В количество узлов, лежащих внутри прямоугольника, а через Г – количество узлов на его границе. Сместим сетку на полклетки вправо и полклетки вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещённой сетки, а каждый из Г узлов – 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника
Пусть АВСD – прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки (рисунок 8). Обозначим через В количество узлов, лежащих внутри прямоугольника, а через Г – количество узлов на его границе. Сместим сетку на полклетки вправо и полклетки вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещённой сетки, а каждый из Г узлов – 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника 
 тметим узлы (пересечение линий) на границе пятиугольника и внутри пятиугольника:
тметим узлы (пересечение линий) на границе пятиугольника и внутри пятиугольника: айдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S= В +
айдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S= В +  Задача 10. Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 × 1см в масштабе 1 см – 100 м (рисунок 12).
Задача 10. Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 × 1см в масштабе 1 см – 100 м (рисунок 12).

 еорг Алекса́ндр Пик (нем. Georg Alexander Pick; 10 августа 1859 г. – 13 июля 1942 г.) – австрийский математик. В 16 лет Георг окончил школу и поступил в Венский университет. В 20 лет получил право преподавать физику и математику. 16 апреля 1880 года под руководством Лео Кёнигсбергера Пик защитил докторскую диссертацию «О классе абелевых интегралов». В 1881 году он получил место ассистента у Эрнста Маха, который занял кафедру физики в Пражском университете. Чтобы получить право чтения лекций, Георгу необходимо было пройти хабилитацию. Для этого он написал работу «Об интеграции гиперэллиптических дифференциалов логарифмами». Это произошло в 1882 году, вскоре после разделения Пражского университета на чешский (Карлов университет) и немецкий (Университет Карла-Фердинанда). Пик остался в Немецком университете. В 1884 году Пик уехал в Лейпцигский университет к Феликсу Клейну. Там он познакомился с другим учеником Клейна, Давидом Гильбертом. Позже, в 1885 г., он вернулся в Прагу, где и прошла оставшаяся часть его научной карьеры. Преподавательская деятельность в Немецком университете в Праге в 1888 г. Пик получил место экстраординарного профессора математики, затем в 1892г. стал ординарным профессором. В 1910 г. Георг Пик был в комитете, созданном Немецким университетом Праги для рассмотрения вопроса о принятии Альберта Эйнштейна профессором в университет. Пик и физик Антон Лампа были главными инициаторами этого назначения, и благодаря их усилиям Эйнштейн, с которым Пик впоследствии сдружился, в 1911г. возглавил кафедру теоретической физики в Немецком университете в Праге. Круг математических интересов Пика был чрезвычайно широк. В частности, им написаны работы в области функционального анализа и дифферен-циальной геометрии, эллиптических и абелевых функций, теории дифференциальных уравнений и комплексного анализа, всего более 50 тем. С его именем связаны матрица Пика, интерполяция Пика - Неванлинны, лемма Шварца-Пика. Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники. [8]
еорг Алекса́ндр Пик (нем. Georg Alexander Pick; 10 августа 1859 г. – 13 июля 1942 г.) – австрийский математик. В 16 лет Георг окончил школу и поступил в Венский университет. В 20 лет получил право преподавать физику и математику. 16 апреля 1880 года под руководством Лео Кёнигсбергера Пик защитил докторскую диссертацию «О классе абелевых интегралов». В 1881 году он получил место ассистента у Эрнста Маха, который занял кафедру физики в Пражском университете. Чтобы получить право чтения лекций, Георгу необходимо было пройти хабилитацию. Для этого он написал работу «Об интеграции гиперэллиптических дифференциалов логарифмами». Это произошло в 1882 году, вскоре после разделения Пражского университета на чешский (Карлов университет) и немецкий (Университет Карла-Фердинанда). Пик остался в Немецком университете. В 1884 году Пик уехал в Лейпцигский университет к Феликсу Клейну. Там он познакомился с другим учеником Клейна, Давидом Гильбертом. Позже, в 1885 г., он вернулся в Прагу, где и прошла оставшаяся часть его научной карьеры. Преподавательская деятельность в Немецком университете в Праге в 1888 г. Пик получил место экстраординарного профессора математики, затем в 1892г. стал ординарным профессором. В 1910 г. Георг Пик был в комитете, созданном Немецким университетом Праги для рассмотрения вопроса о принятии Альберта Эйнштейна профессором в университет. Пик и физик Антон Лампа были главными инициаторами этого назначения, и благодаря их усилиям Эйнштейн, с которым Пик впоследствии сдружился, в 1911г. возглавил кафедру теоретической физики в Немецком университете в Праге. Круг математических интересов Пика был чрезвычайно широк. В частности, им написаны работы в области функционального анализа и дифферен-циальной геометрии, эллиптических и абелевых функций, теории дифференциальных уравнений и комплексного анализа, всего более 50 тем. С его именем связаны матрица Пика, интерполяция Пика - Неванлинны, лемма Шварца-Пика. Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники. [8]









