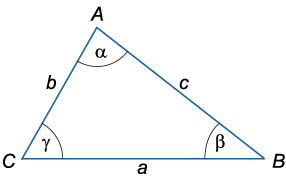
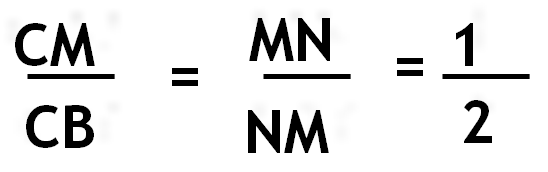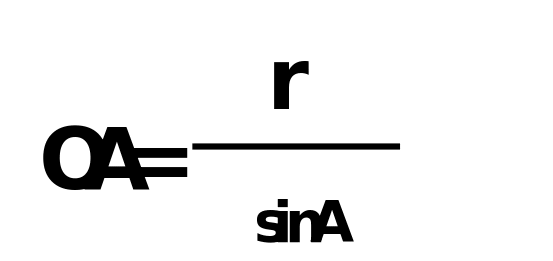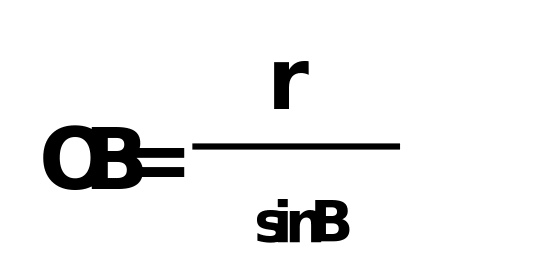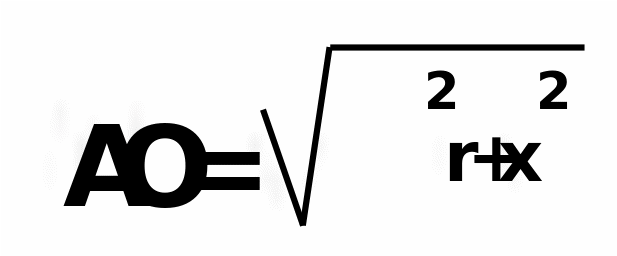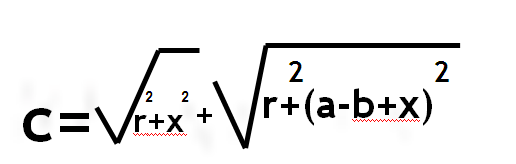| 10. | Задачи | Задача 1. Через вершину С треугольника АВС проведена прямая параллельная его биссектрисе АА1, и пересекающая прямую АВ в точке D. Докажите,что AC=AD. 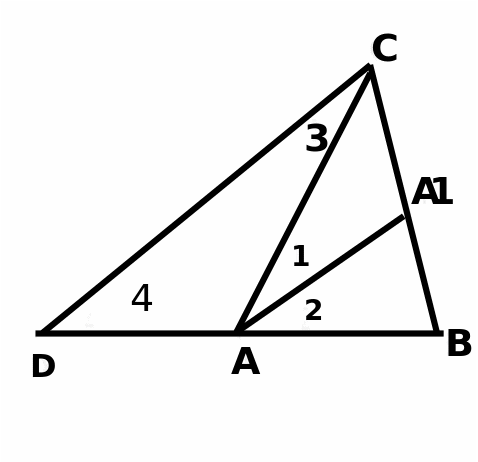
Решение:
1 Способ: 1.)угол 3=углу 1(т.к.накрест лежащие, при DC||AA1) 2)угол4=углу 2(т.к они соответственные при DC||AA1) 3) угол 3=углу 1=углу2=углу 4 Тогда треугольник DCA – равнобедренный т.е. AC=AD ч.т.д 2Способ: DC||AA1,тогда угол 3 = углу 1(накрест лежащие) Угол САВ - внешний для треугольника DCA. Угол САВ=угол 4+угол 3, но угол САВ=угол1+ угол2 Угол 1+угол 2=угол 4+угол 3, с учетом п.1 заключаем, что угол 4= углу 2 3)тогда угол 3=углу 1=углу 2=углу 4, угол 4 = углу 3 , треугольник DCA равнобедренный т.е. АС=AD ч.т.д.
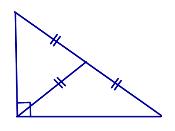
| Задача 2. Медиана и высота треугольника, проведенные из одной вершины треугольника, делят этот угол на три равные части. Доказать, что треугольник прямоугольный.
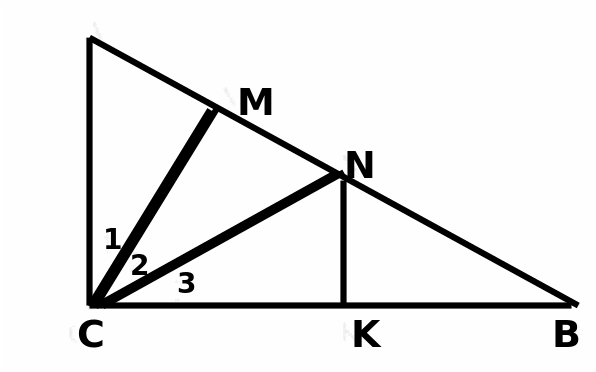
Решение: Треугольник АСВ, СМ – высота ,CN- медиана ,т.е.AN=NB. 1 Способ: 1.)треугольник АСМ=NCM- прямоугольные , т.к. СМ - общая, угол 1 = углу 2. 2) Из равенства треугольников следует: AM=MN и AC=CN. 3) Т.к. CN - медиана ,т.е. AN = NB. То MC=0.5AN=0.5NB. 4) Проведем NK, NK перпендикулярно ВС. 5) треугольник CMN= треугольнику CNK – прямоугольные, CN – общая, угол2 = углу 3, MN=NK=0.5NB. 6) треугольник NKB : угол NKB – 90° . NK=0.5NB,тогда угол NBC=30°. 7) треугольник СМВ : угол MCB= 90°- 30°=60°. то угол 2=30° н угол 1=30°. Следовательно угол ACB = 90° . 2 способ: 1) Очевидно треугольник AСМ подобен треугольнику АВС. Из подобия треугольников следует угол 1= углу ACM = углу B 2) треуг.САМ = треуг.CNM - прямоугольные (общая сторона СМ, угол l = углу 2). Тогда AC=CN. Отсюда, треугольник ACN - равнобедренный. 3) треуг.ACN : СМ - биссектриса, высота, медиана. Следовательно, 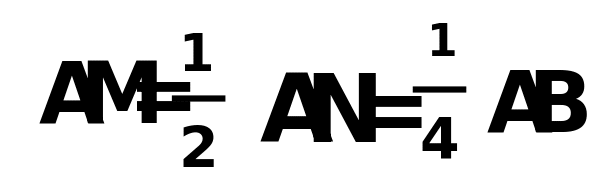 В прямоугольном треугольнике СМВ :CN - биссектриса угла MCB. По свойству биссектрисы треугольника 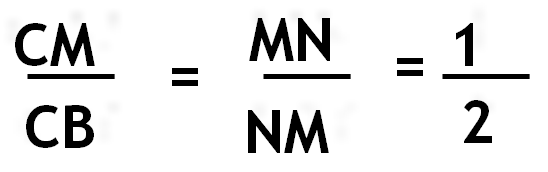 Т.е. СМ =0.5СВ . Что означает: угол В = 30 градусам. 5) но угол B= углу 1 = углу 2 = углу 3 = 30 градусам, угол C =3* угол1=90°.
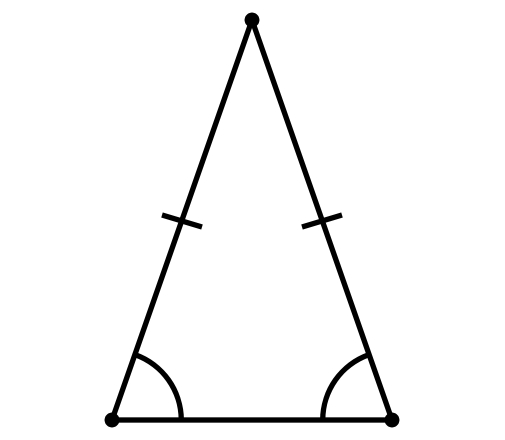
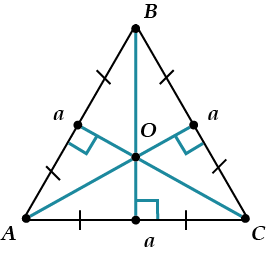
| Задача 3. На высоте равнобедренного треугольника АВС (АВ = ВС) ВВ1,, взята точка D. Докажите,, что : I) треугольник АВD = треугольнику BDC 2) треугольник ADB1=треугольнику DB1C.
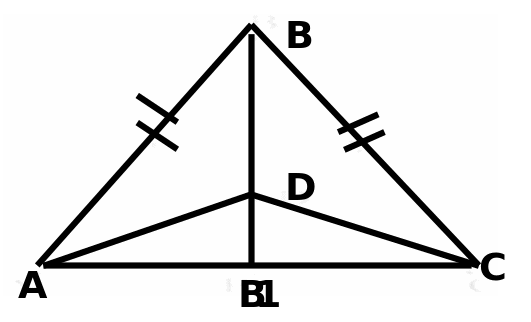
Решение: Первая часть - равенство треугольников ABD и BDC докатывается Легко. Рассмотрим способы доказательства второго равенства.
1 Способ: Треугольник ADB1= треугольнику DB1C т.к. а) AD=DC из равенства треугольников ABD и В DC, б) B1D-общая. в) угол ADB1 = углу В1DC (т.к. смежные с ними углы ADB и BDC равны из равенства треугольников ABD и BDC).
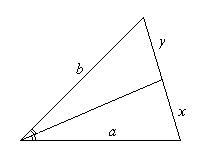
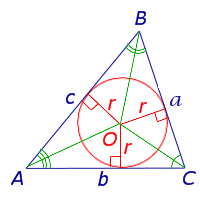
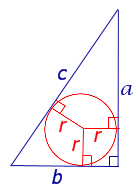
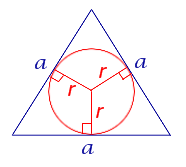
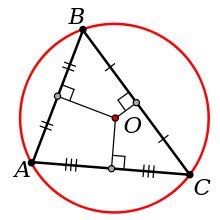
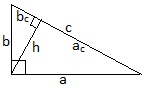
2 способ. Треугольник ADC - равнобедренный (из равенства треугольников ABD и BDC). DB1- высота этого треугольника, а значит и биссектриса угла ADC. Тогда треугольник ADB1= треугольнику DB1C по двум сторонам и углу между ними.) 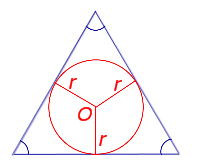 | Задача 4. Стороны треугольника a,b,c. Найдите радиус окружности, имеющей свой центр на стороне с и касающейся 2-х других сторон a и b. (a,b,c- заданные числа.)
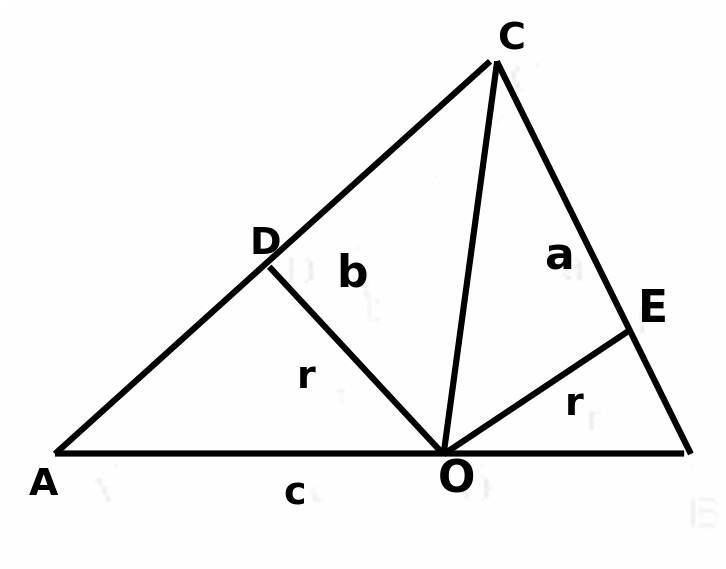 Решение:
1 способ: 1.) углы А и В находим по теореме косинусов. 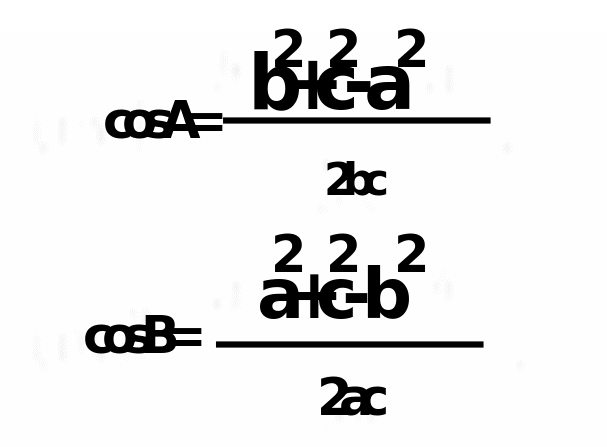 2.) из треугольника ADO 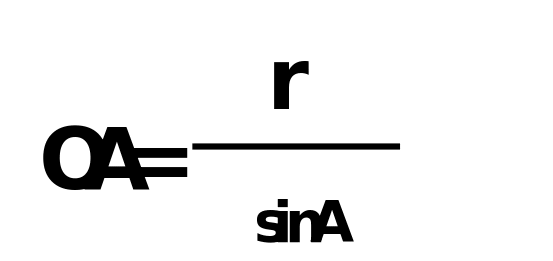 3.) из треугольника OEB 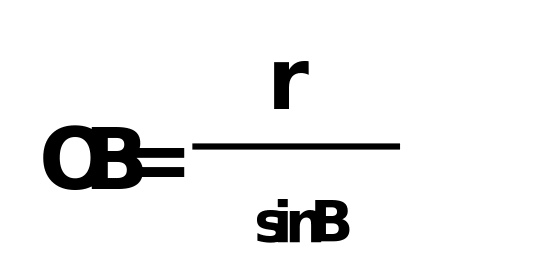 4.)из уравнения 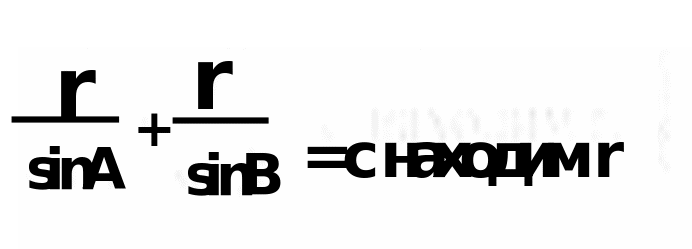
2 способ: 1.) обозначим AD через х 2.)из треугольника AOD 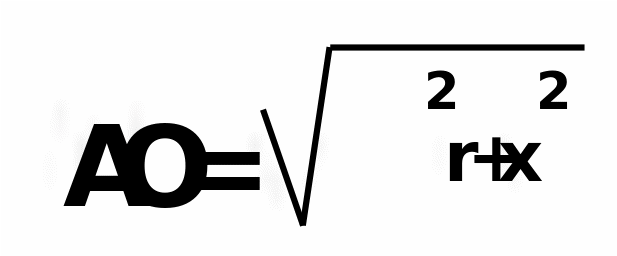 3.) из треугольника COD 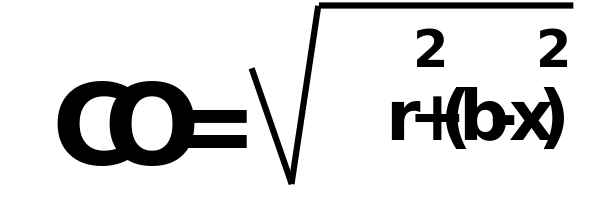 4.) CE=CD=b-x( по свойству касательны, проведенных из одной точки) 5.) BE=a-b+x 6.)из треугольника OBE 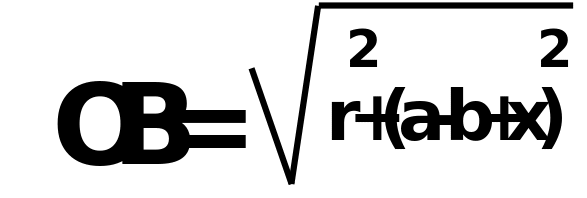 7.) решим уравнение 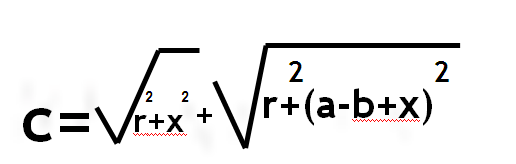 |








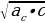
 =
=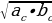
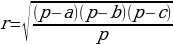
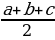

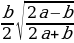
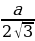
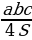
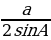
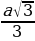
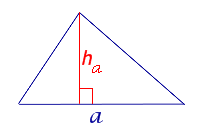
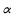
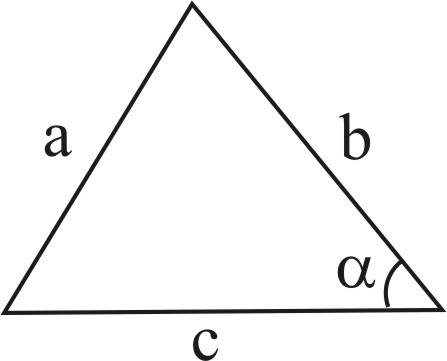
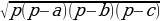
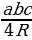
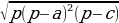
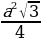
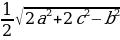
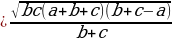
 bc
bc