Сравнение обыкновенных дробей.

5 класс.

ГЛАВА 2. ДРОБНЫЕ ЧИСЛА.

§ 5. Обыкновенные дроби.

п. 24. Сравнение дробей.

Круг, как и любую другую фигуру, можно разделить на равные части разными способами. На рисунке первый круг разделили на две равные части, а другой – на четыре равные части. На первом рисунке закрасили голубым цветом одну часть, а на втором – две части. Как видно из рисунка .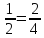

Посмотрим, где на координатном луче располагаются эти числа.

Числа и являются координатами одной и той же точки. Значит, эти дроби равны.

Сравним дроби и . Отметим их на координатном луче:

Дробь находится правее дроби , значит, она больше.

Из двух чисел на координатном луче больше то, которое находится правее.

Итак, . Логично правило:

Из двух дробей с одинаковыми знаменателями больше та, у которой больше числитель.

Теперь сравним дроби и . Отметим их на координатном луче.

Как видно из рисунка, находится правее, значит, .

Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.

1. Начертить координатный луч с единичным отрезком 24 клетки. Отметить на нём дроби . С помощью координатного луча сравнить дроби:

. Записать в виде неравенств.

1. Сравнить дроби:

   1) и	2) и	3) и	4) и
   5) и	6) и	7) и	8) и

2. Расставить дроби в порядке возрастания:

3. Расставить дроби в порядке убывания:

4. Выберите из предложенных три наибольшие дроби:

1. Выберите из предложенных четыре наименьшие дроби:

1. Выберите из предложенных равные друг другу дроби:

3
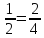