СТEРЕОМЕТРИЯ ЕСЕПТЕРІ
1. Шардың өзара перпендикуляр екі қимасының ортақ хордасының ұзындығы 12. Қималарының аудандары 100π, 64πболса, шардың радиусын тап.
Шешуі: АВ - хорда , ОҒ - шардың радиусы
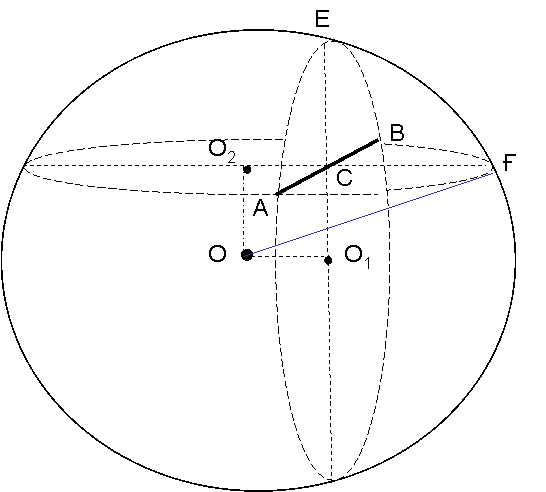
Алдымен, О1Е және О2Ғ – қималардың радиустарын тауып алайық.
π·О1Е2 = 100π және π·О2Ғ2 = 64π
О1Е = 10 және О2Ғ = 8
1) ΔАСО1: АС = 6; АО1= О1Е = 10
О1С2 = АО12 – АС2
О1С2 = 102 - 62
О1С2 = 64
О1С = 8
2) ΔОО2Ғ: ОО2 = О1С = 8
ОҒ2 = ОО22 +О2Ғ2
ОҒ2 = 82 +82
ОҒ2 = 128
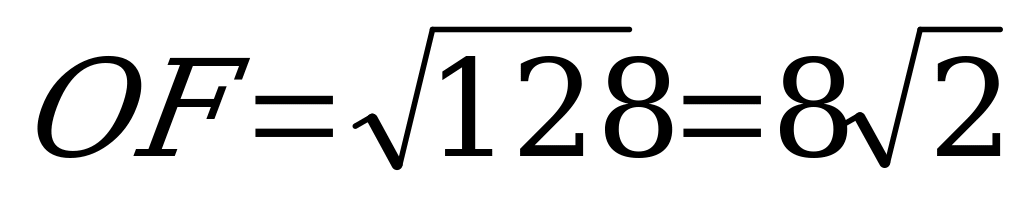
Жауабы: 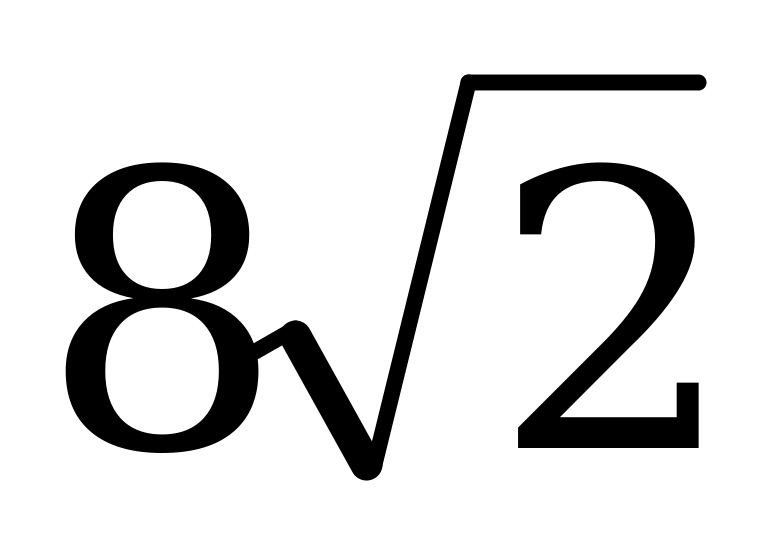
№2 Шардың үлкен дөңгелегінің ауданы 50π. Шардың өзара перпендикуляр қималарының ортақ хордасының ұзындығы 6 см. Егер бір қимасының ауданы 25π болса, шардың центрінен қималарының жазықтығына дейінгі қашықтықты тап.
Шешуі: шардың центрінен қималардың жазықтығына дейінгі ара қашықтықтар ОО1 және ОО2-ны табу керек. Ол үшін:
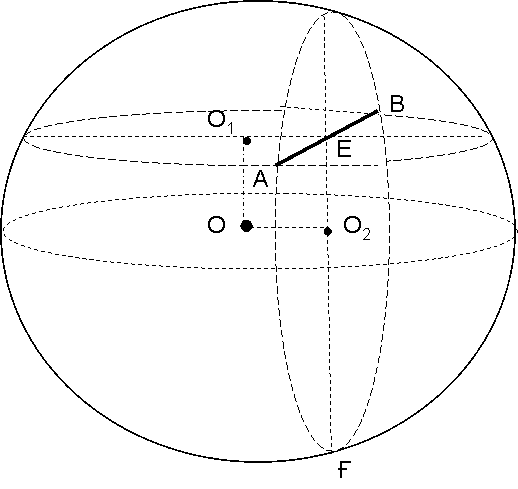
1) шардың үлкен дөңгелегінің ауданы белгілі, ендеше шардың радиусы
R – ді тауып алайық, S=πR2
πR2 = 50π
R2 = 50
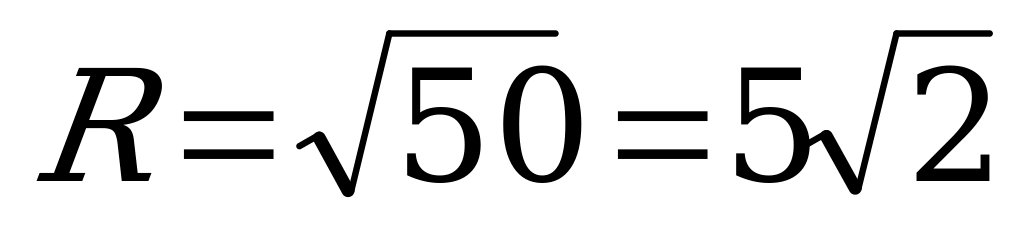
ОҒ = R =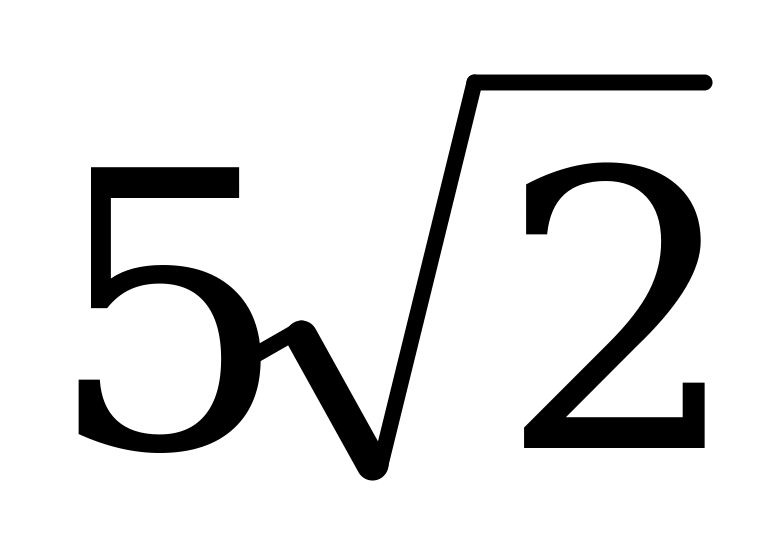
2) Есеп шарты бойынша шардың бір қимасының ауданы 25π. Осы қиманың радиусы О1В –ның мәнін табайық.
S=πR2
π·О1В2 = 25π
О1В2 = 25
О1В = 5 см.
3) ΔВО1Е - тік бұрышты, АЕ = 3см. О1В = 5 см.
О1Е2 = О1В2 – АЕ2
О1Е2 = 52 – 32
О1Е2 = 16
О1Е = 4 см
О1Е = ОО2 = 4 см
4) ΔОО2Ғ - тік бұрышты, ОО2 = 4см. ОҒ = 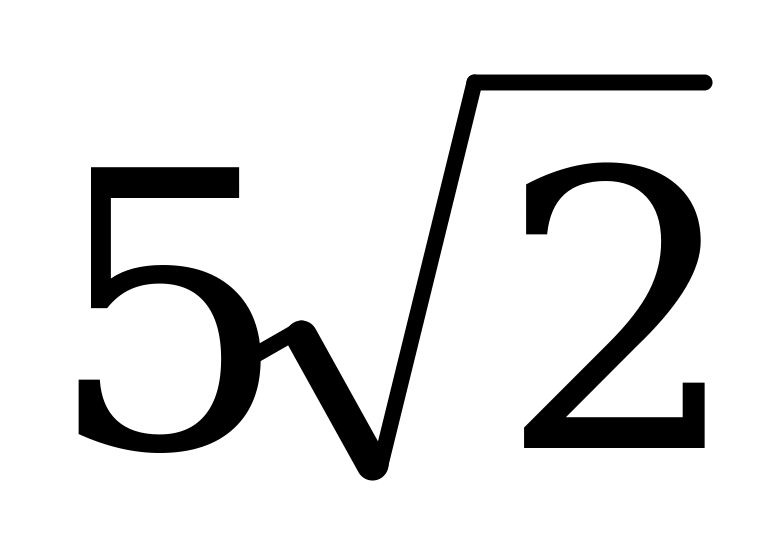 см.
см.
О2Ғ2 = ОҒ2 – ОО22
О2Ғ2 = (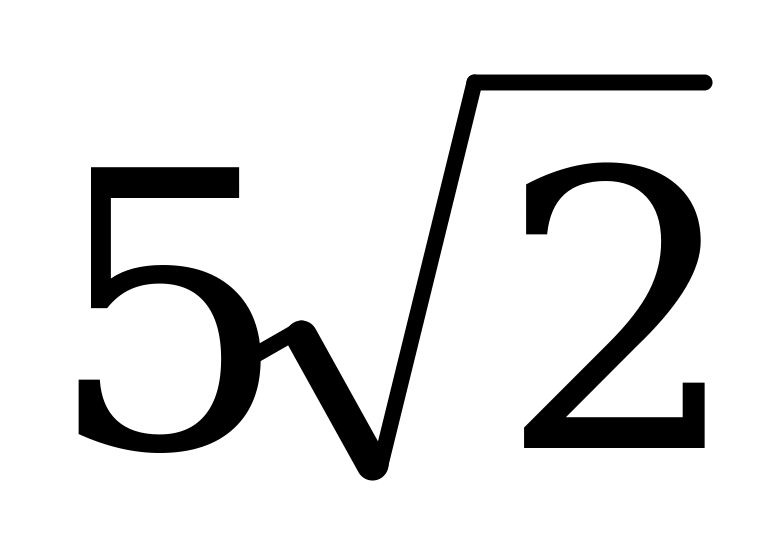 )2 – 42
)2 – 42
О2Ғ2 = 34
О2Ғ = 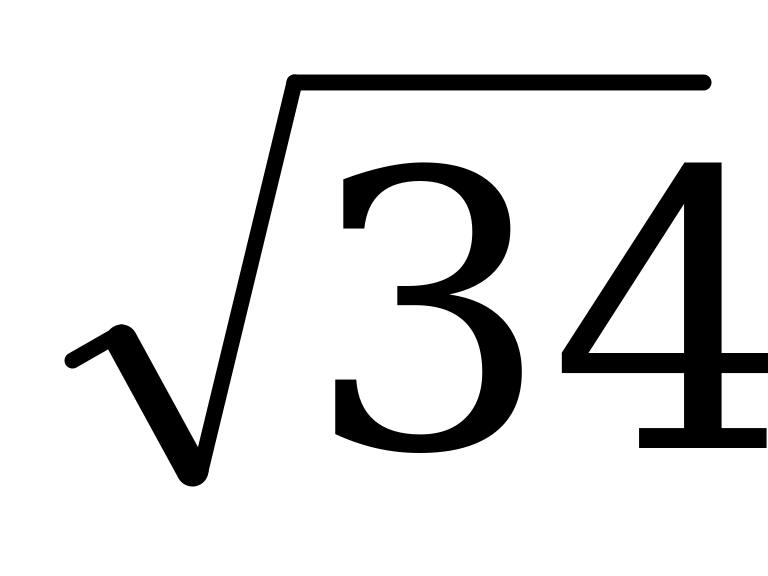 см
см
О2Ғ = АО2 = 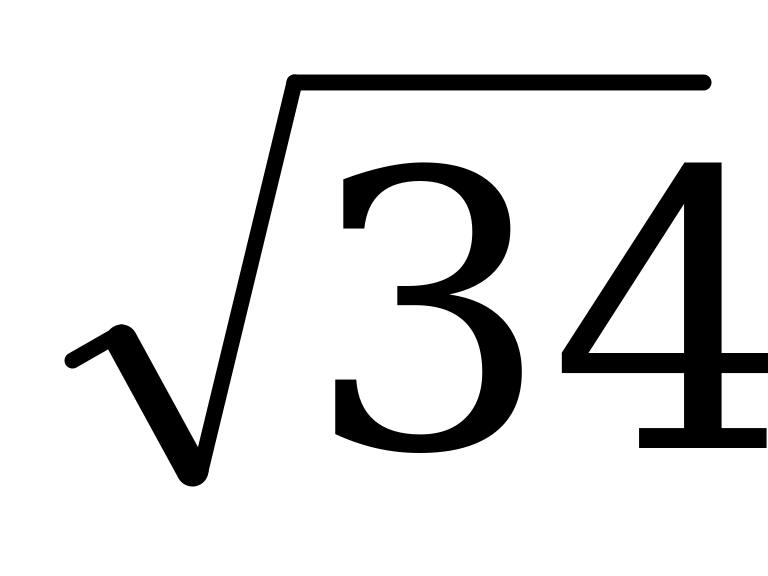 см
см
5) ΔАО2Е - тік бұрышты үшбұрышын қарастырамыз, АЕ = 3см. АО2 = 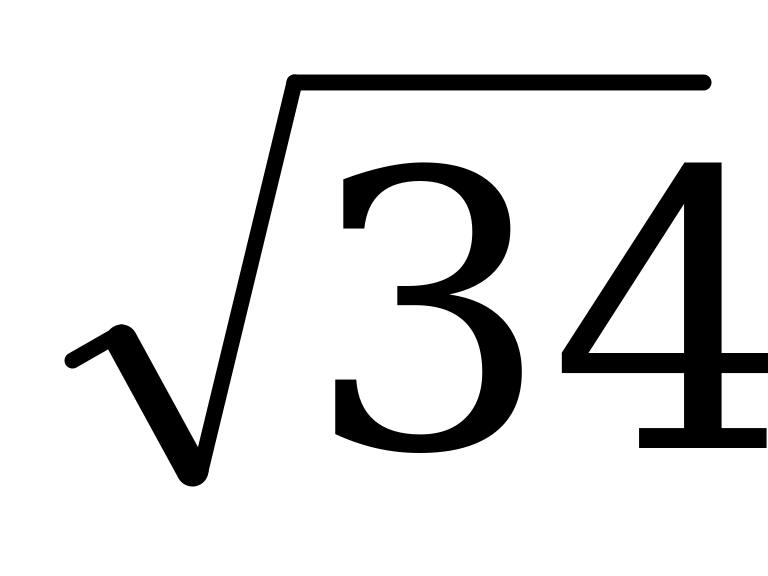 см
см
О2Е2 = АО22 – АЕ2
О2Е2 = (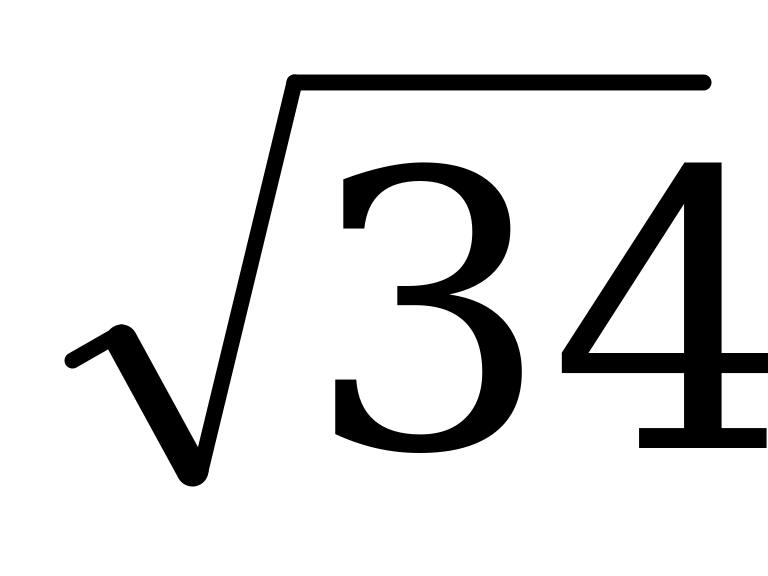 )2 – 32
)2 – 32
О2Е2 = 25
О2Е = 5 см
Сонымен, О2Е = ОО1= 5 см
Жауабы: ОО1= 5 см ОО2 = 4 см
3. Табанының қабырғасы 9 см және биіктігі 10 см болатын үшбұрышты дұрыс пирамидаға сырттай шар сызылған. Шар радиусын тап.
Б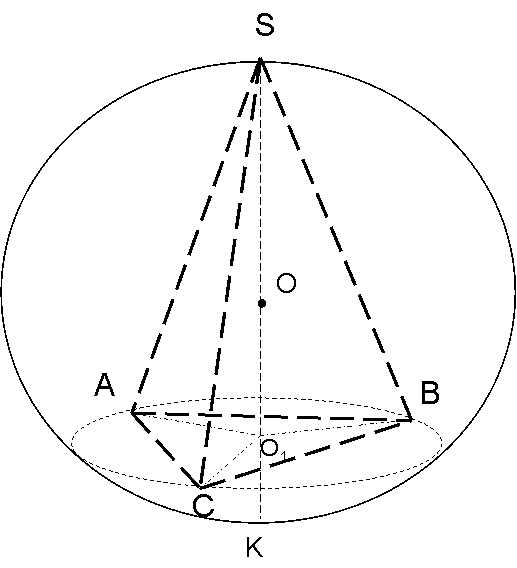 ерілгені: пирамида, шар
ерілгені: пирамида, шар
ΔАВС - тең қабырғалы: АВ=а = 9 см.
SO1 = H = 10 см.
т/к: SO - шар радиусы
Шешуі:
1-тәсіл:
SK – шардың диаметрі. SO - шардың радиусы және SO = ½*SK. ендеше шардың радиусын табу үшін SK диаметрін тапсақ болғаны.
1) Алдымен, О1В – АВС үшбұрышына сырттай сызылған шеңбер радиусының мәнін есептейік. /R=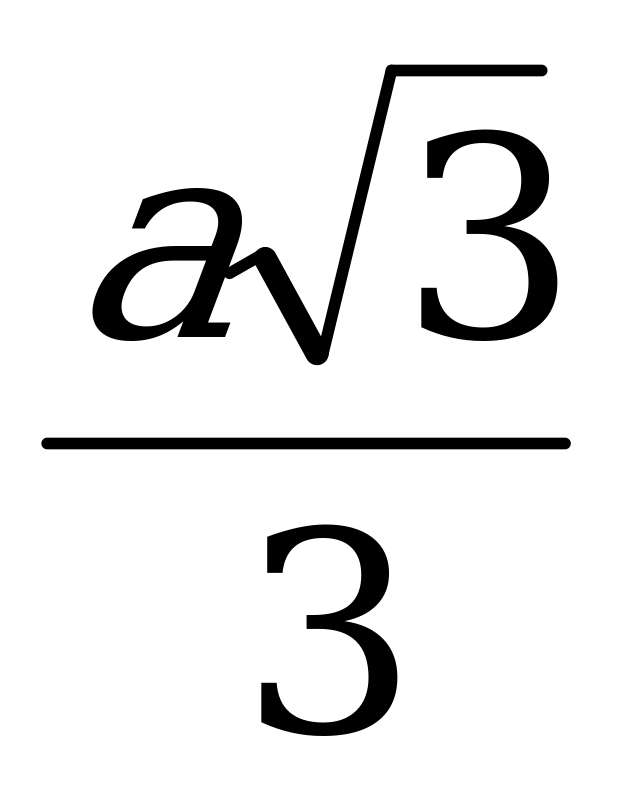 формуласы бойынша/
формуласы бойынша/
О1В = 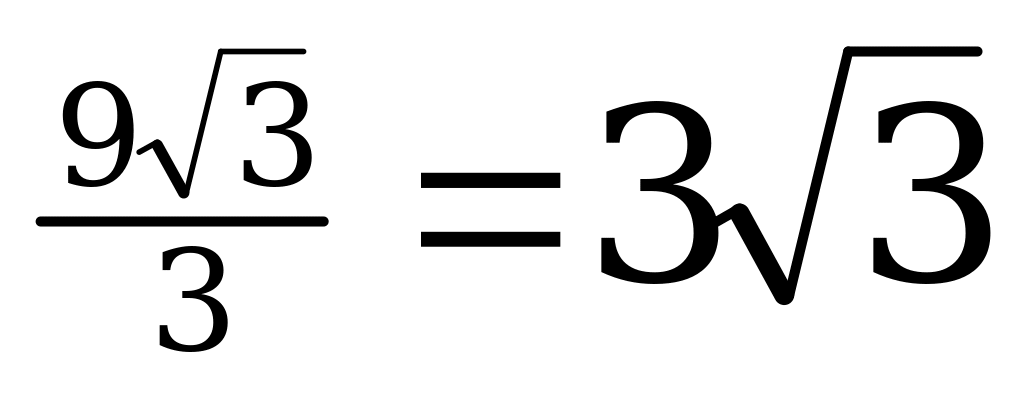
О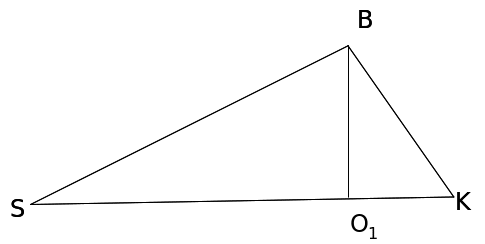 1В=
1В=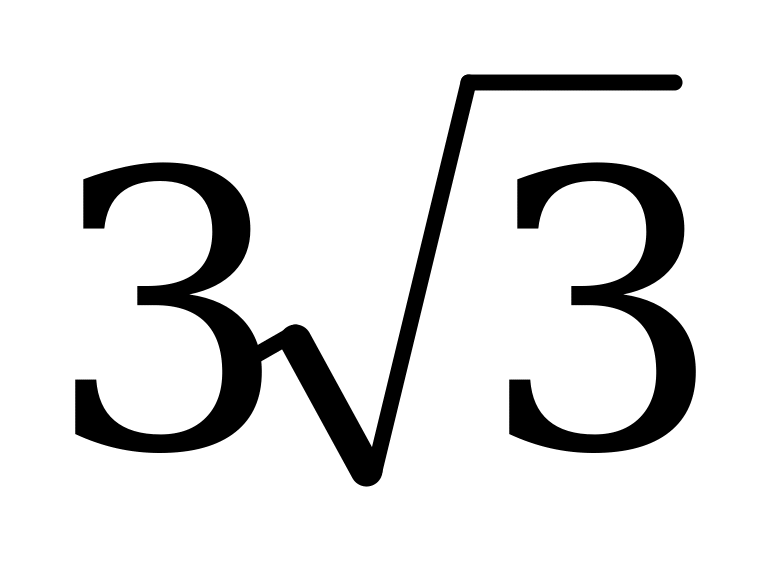
2) ΔSВК – тік бұрышты, О1К = х см, SО1= 10 см, ВО1= 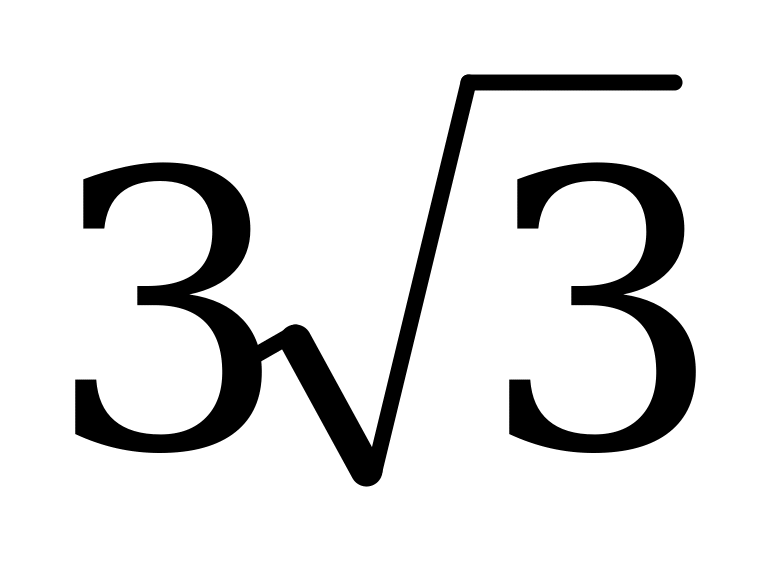 см.
см.
ВО1=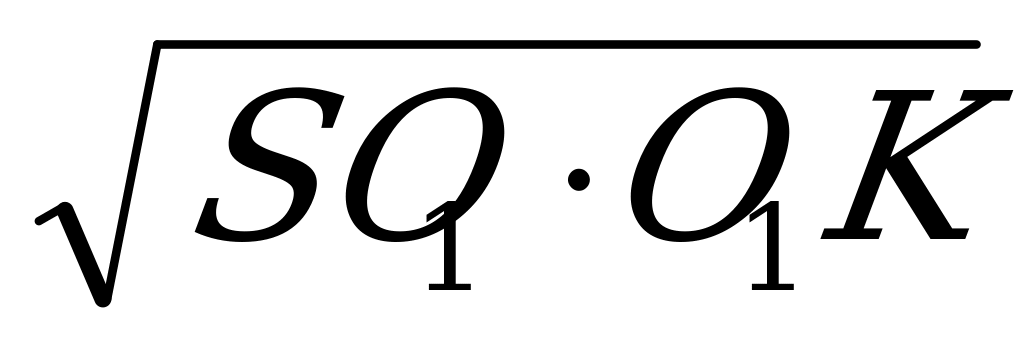 (тік бұрышты үшбұрыштың гипотенузаға жүргізілген биіктігі)
(тік бұрышты үшбұрыштың гипотенузаға жүргізілген биіктігі)
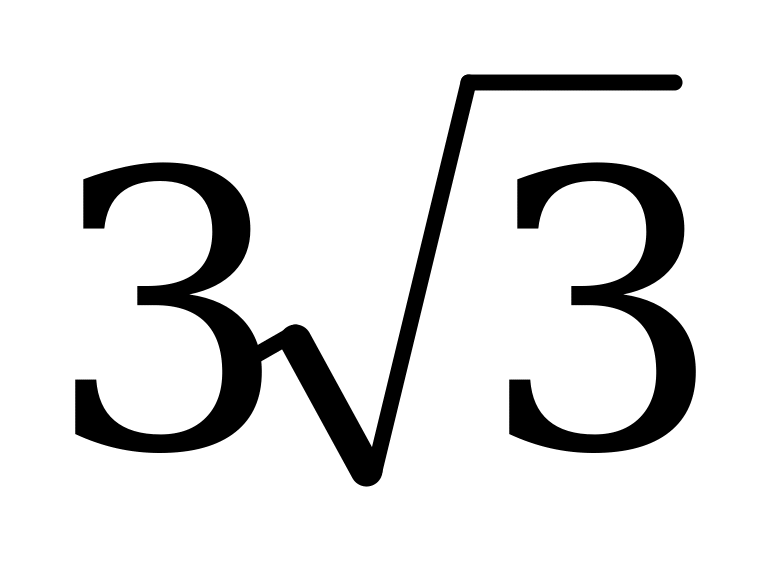 =
=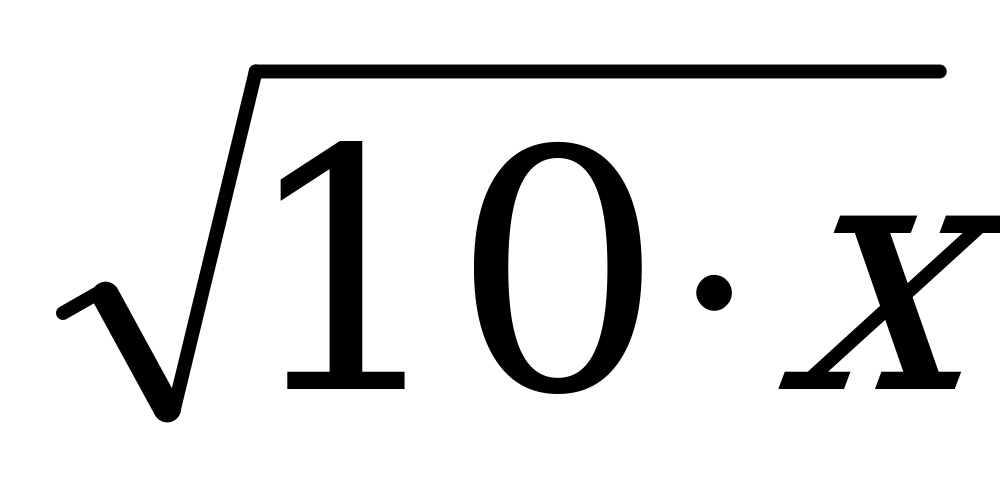 (екі жағын квадраттаймыз)
(екі жағын квадраттаймыз)
10х=27
х = 2,7
Сонда: О1К = 2,7см.
3) SК= SО1 + О1К
SК = 10 + 2,7 = 12,7
SO = ½*SK
SO = 12,7 : 2 = 6,35
2-тәсіл: (формула бойынша)
Есеп шартында пирамиданың табан қабырғасы a =9 см және биіктігі
һ = 10см. Осы пирамидаға сырттай сызылған шардың радиусын табу қажет.
Ол үшін 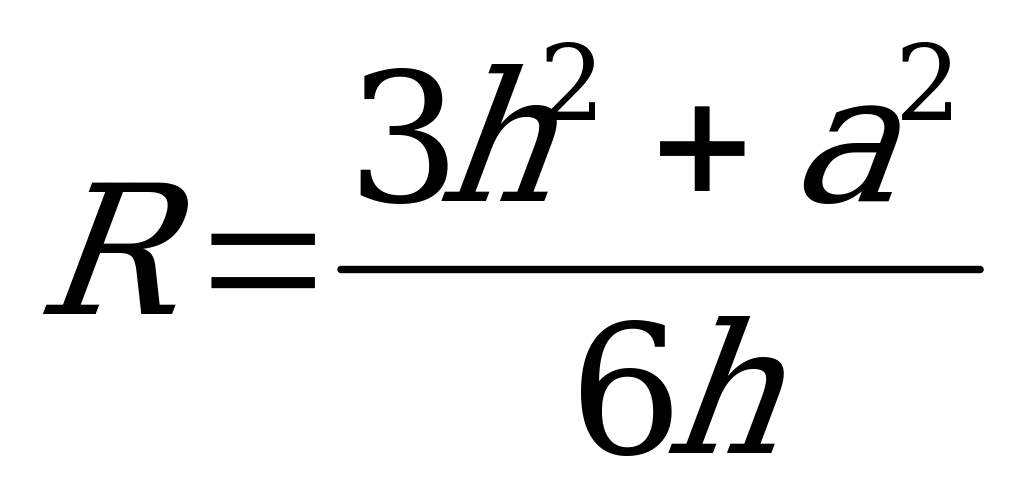 формуласын қолданамыз.
формуласын қолданамыз.
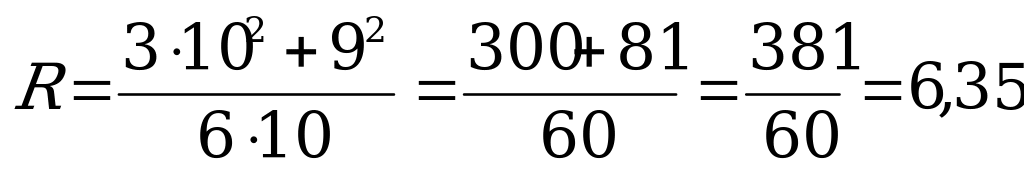
Жауабы: 6,35 см
№4 Сфера радиусы 3 тең бөлікке бөлінгін. Осы нүктелер арқылы радиусқа перпендикуляр жазықтықтар жүргізілген. Қималардың ұзындықтарының айырмасы 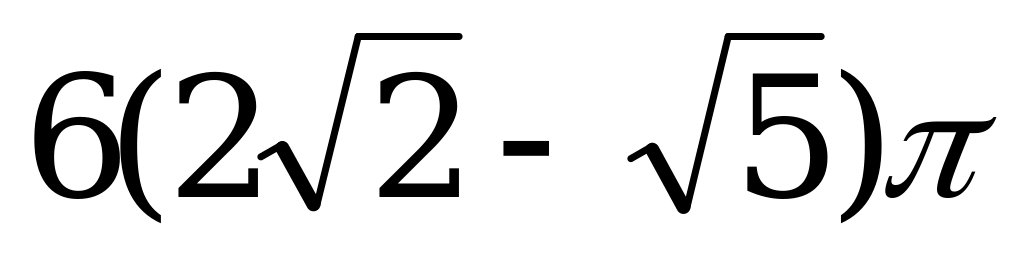 болса, сфераның ауданын тап.
болса, сфераның ауданын тап.
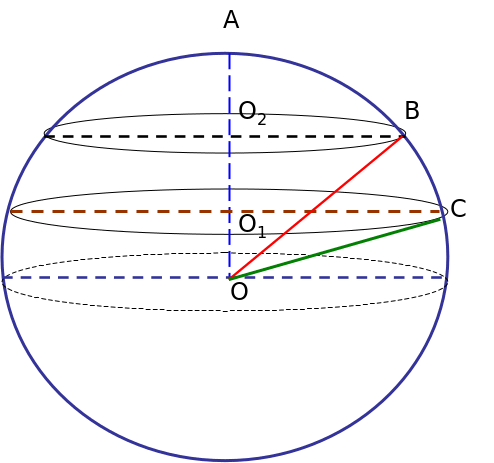
Шешуі: Алдымен, ОА = ОС =ОВ = R ( шар радиусы)
О2В = х және О1С = у деп белгілеп алайық. Сонда:
l2 – l1= 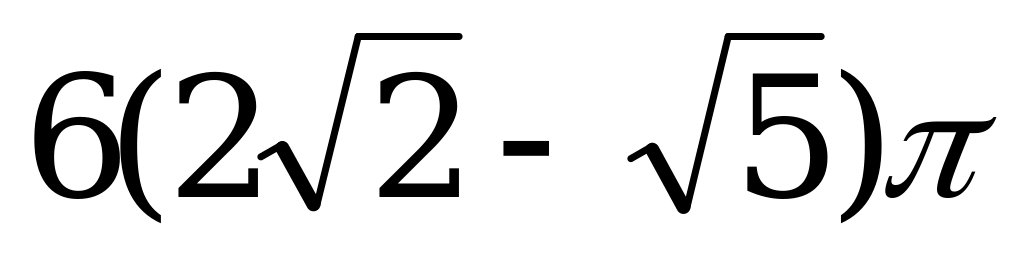 (есеп шарты бойынша)
(есеп шарты бойынша)
2πу - 2πх = 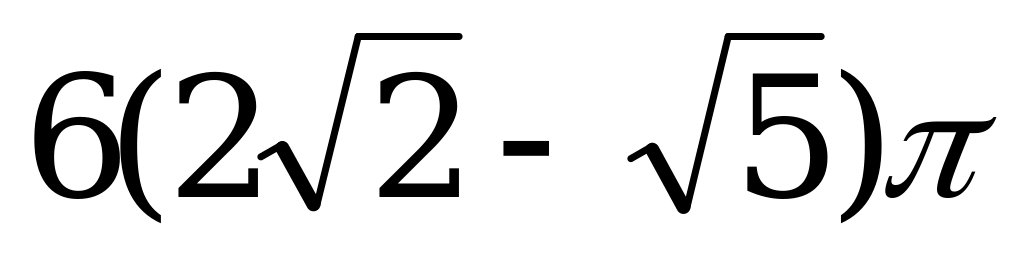
у – х = 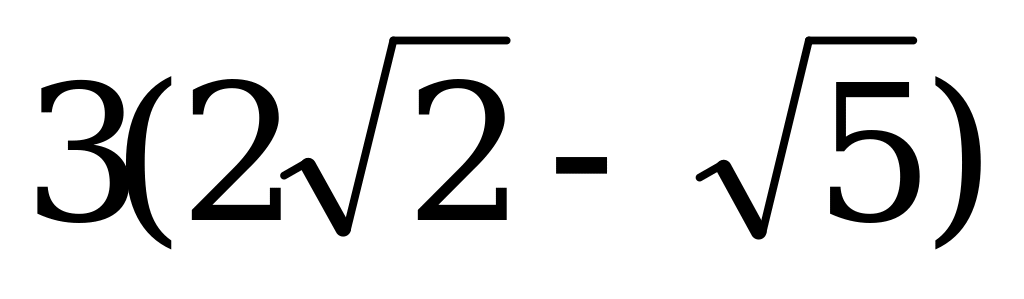 (*)
(*)
1) ΔВОО2: О2В= х және ОО2=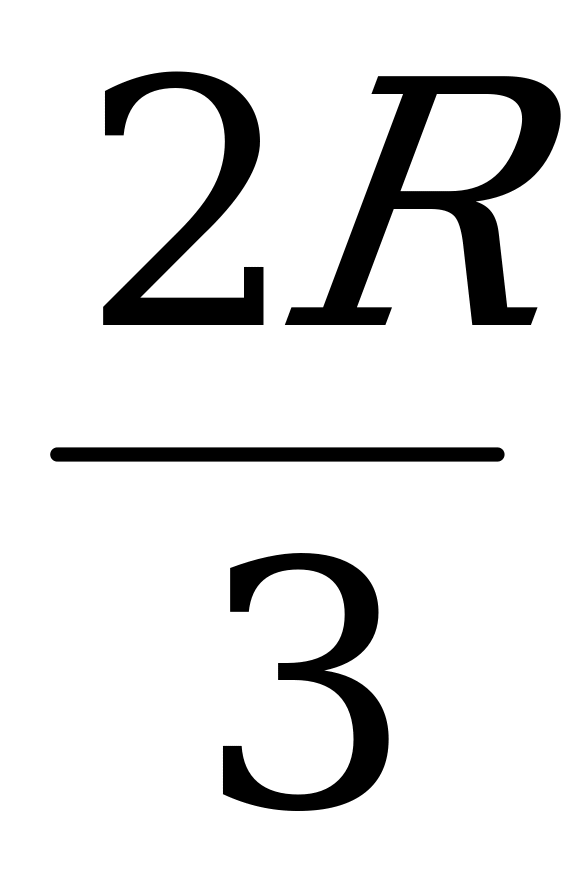
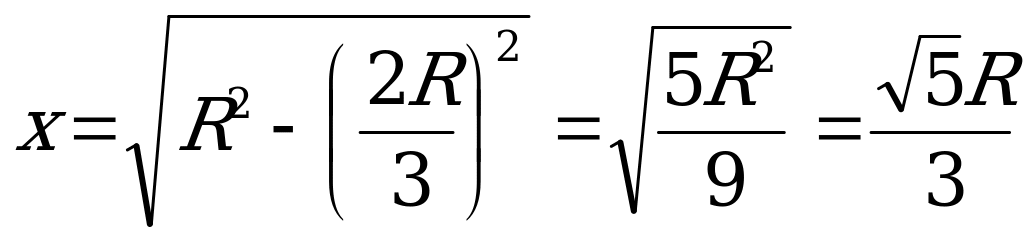
2) ΔСОО1: О1С= у және ОО1=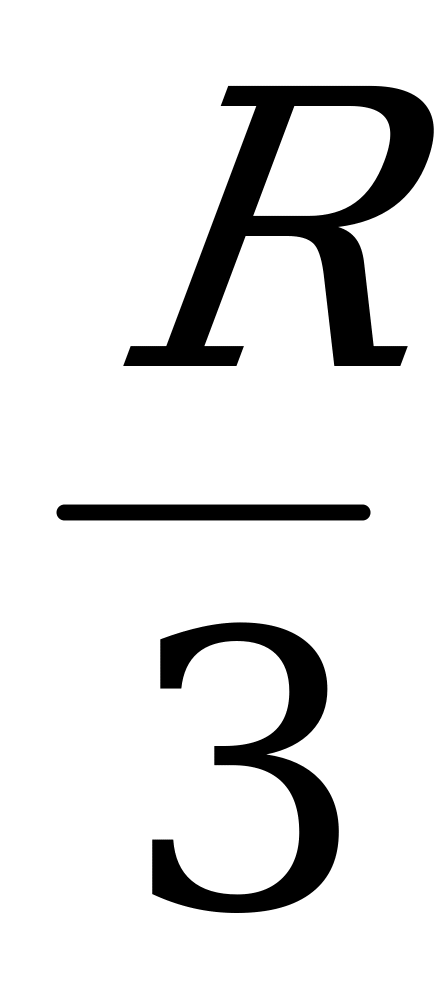
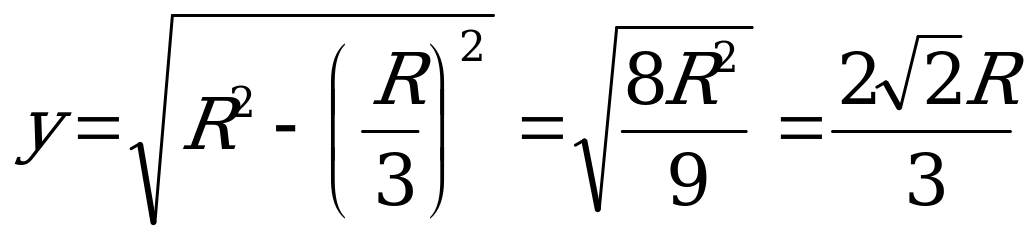
3) (*) –ның орнына х пен у-тің мәнін қойсақ:
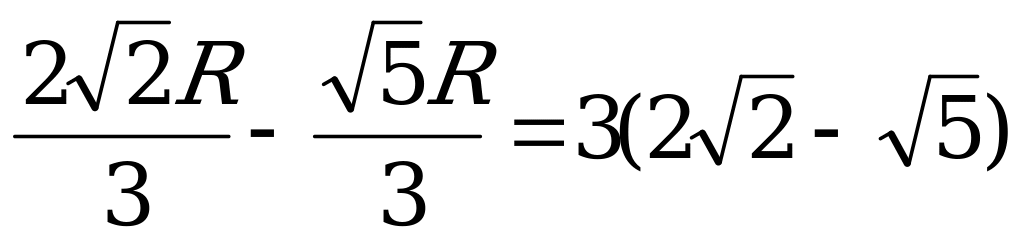
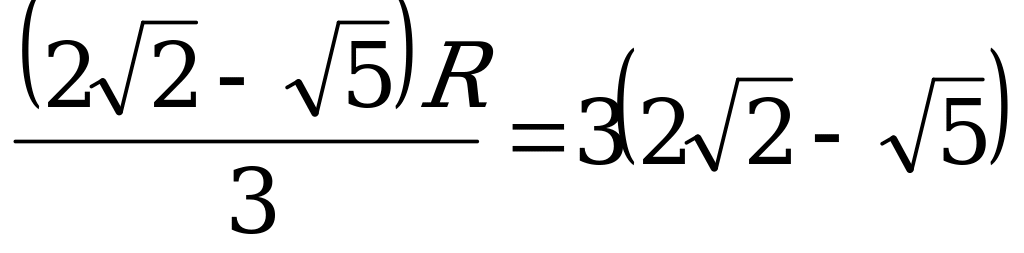
R= 9
4)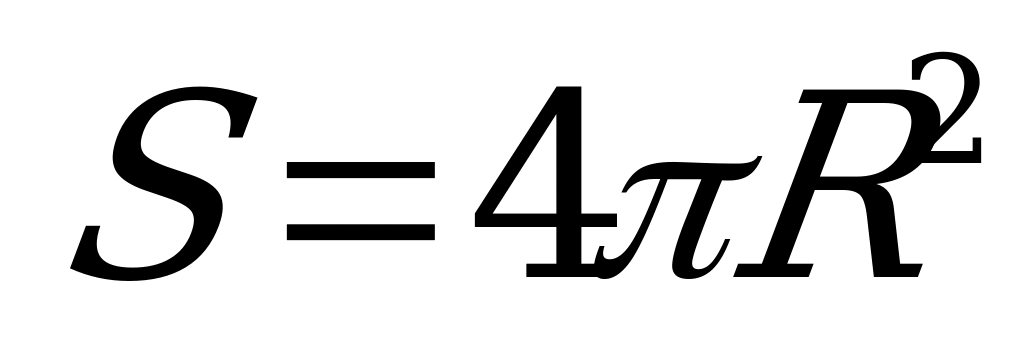
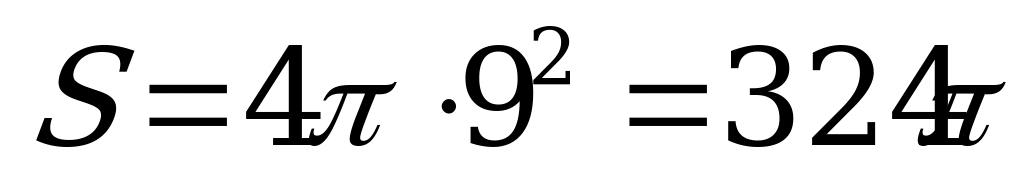
Жауабы: 324π
5.Сфера центрінің бір жағында орналасқан, сфераны қиятын параллель қималардың ұзындығы 10π және 24π . Жазықтықтар арасы 7 см болса, сфера бетінің ауданын табыңдар.
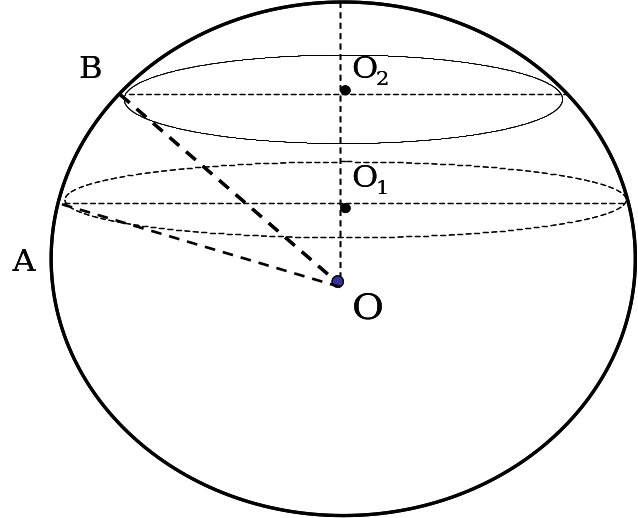
Шешуі: О1О2 = 7см, ОО1= х см, ОО2 = 7 + х, ОВ=R
1) Есеп шарты бойынша қималардың ұзындықтары 10π және 24π . Ендеше олардың радиустары сәйкесінше 5 см және 12 см.
Яғни, О2В = 5 см ; О1А= 12 см.
2) ΔОО2В: ОВ=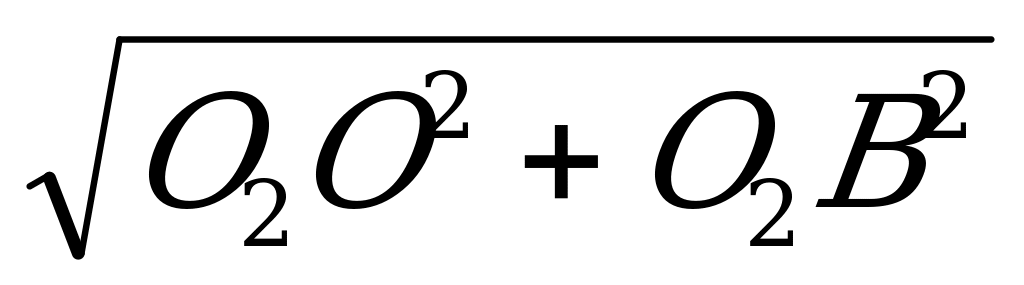
ОВ2 = 52 +(х+7)2
ОВ2 = х2 +14х+74 (*)
3) ΔОО1А: ОА=
ОВ2 = х2 +122
ОВ2 = х2 +144 (**)
4) (*) және (**) теңдіктерінен:
х2 +14х+74 = х2 +144
14х = 70
х = 5
5) R2 = 52 + 144 = 169
R=13 см
6) 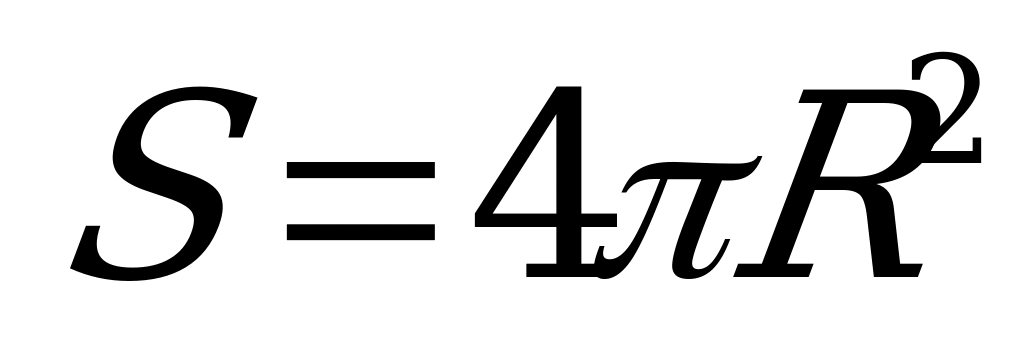
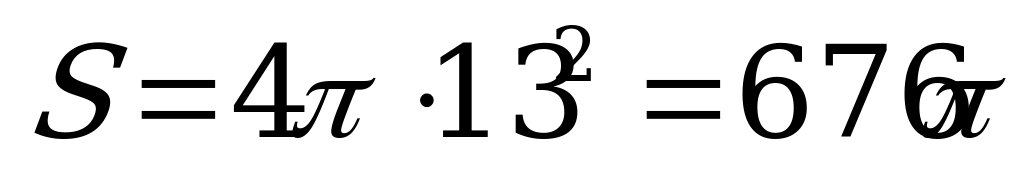
Жауабы: 676 π
8в.8 (2011)
Радиусы 41дм шарды оның центрінен 9дм қашықтықта жазықтық қиып өтеді. Қиманың ауданын табыңдар.
Шешуі: Sқима = π·r2 = π·ВО12
ΔОВО1 – тік бұрышты
О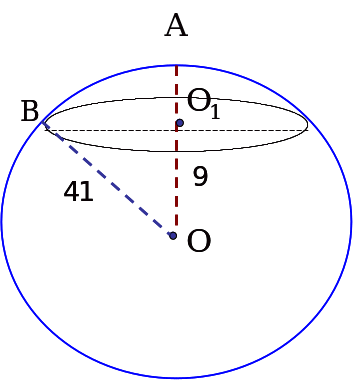 В12= АО2 – ОО12
В12= АО2 – ОО12
ОВ12= 412 – 92 = 1681 - 81=1600
Sқима = π·ВО12= 1600π (дм2)
Жауабы: 1600π
6. Шардың диаметрі 1: 3: 2 қатынасындай бөлінген және осы нүктелер арқылы перпендикуляр жазықтықтар жүргізілген. Егер қималардың аудандарының қосындысы 52π болса, шар бетінің ауданын табыңдар.
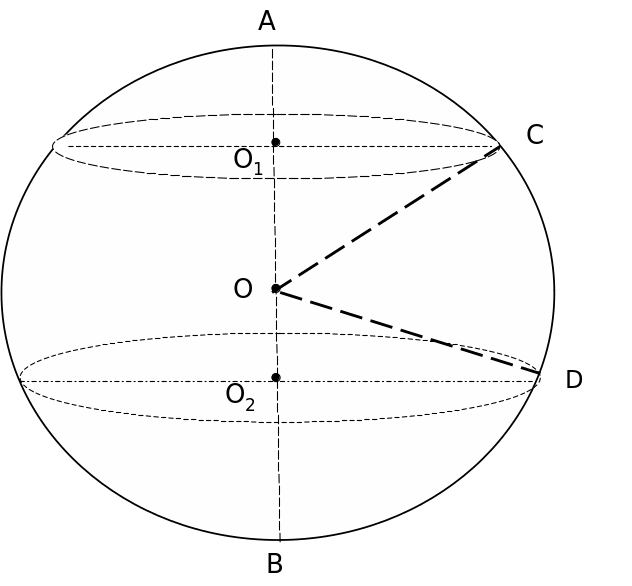
Шешуі: АВ – шардың диаметрі, АВ = 6х (есеп шартынан)
Сонда шардың радиусы R= 3х болады.
1) О1С = R1 және О2D= R2 қималардың радиустары
π(R12 + R22) = 52π
R12 + R22= 52 (*)
2) ΔОО1С: ОС=R= 3х, ОО1 = 2х,
R12 = (3х)2 – (2х)2 = 5х2
3) ΔОО2D: ОD=R= 3х, ОО2 = х,
R22 = (3х)2 – х2 = 8х2
4) (*) орнына мәнін қойсақ:
5х2 + 8х2 = 52
13 х2= 52
х2=4
х=2
5) R= 3х
R= 3·2= 6 (см)
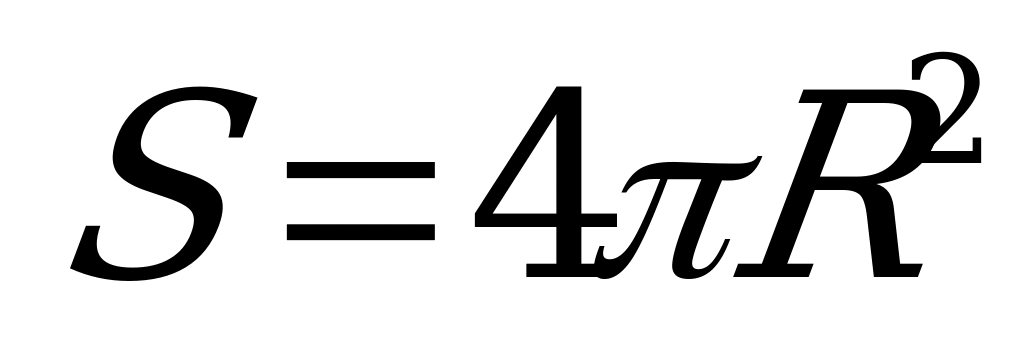
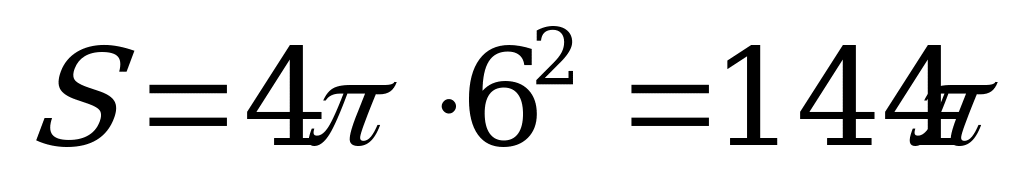
Жауабы: 144 π
7. Радиусы 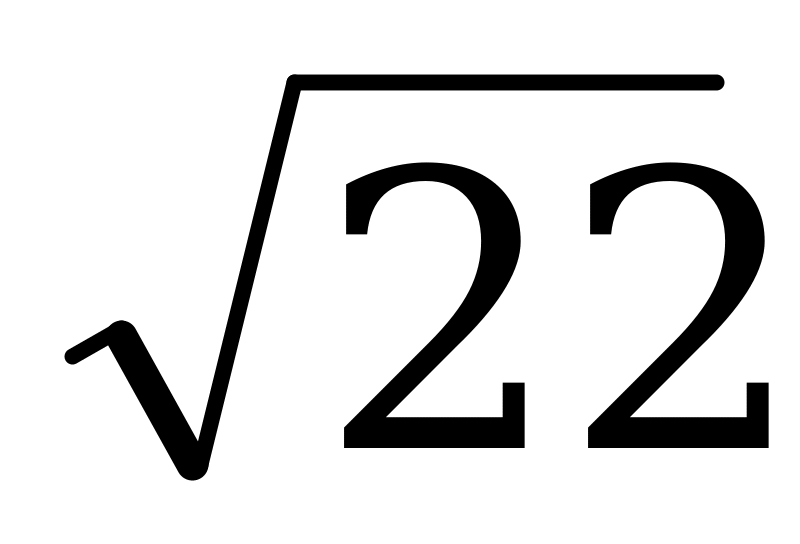 шарға іштей дұрыс АВСА1В1С1 призмасы сызылған. АС1 мен ВСС1 арасындағы бұрыш 45º болса, призма көлемін табыңдар.
шарға іштей дұрыс АВСА1В1С1 призмасы сызылған. АС1 мен ВСС1 арасындағы бұрыш 45º болса, призма көлемін табыңдар.
Шешуі: АО – призмаға сырттай сызылған шардың радиусы. АО =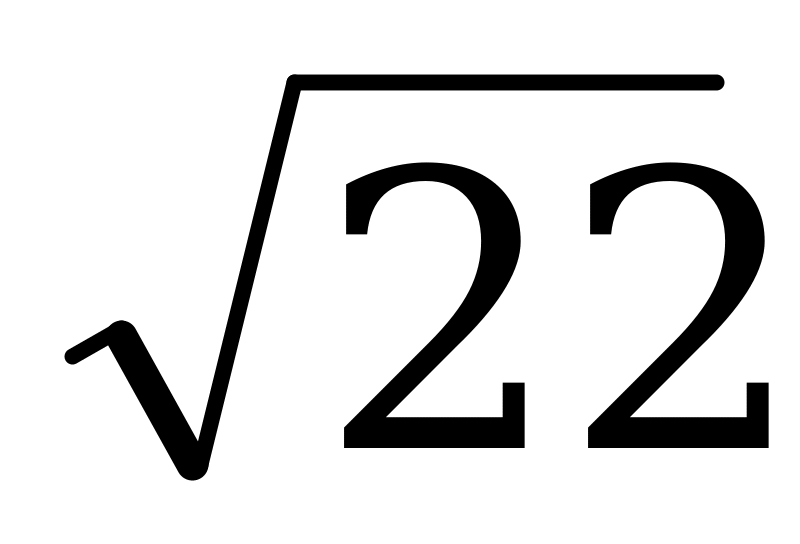 ,
,
Н –призма биіктігі. Призма табанының қабырғасын а деп белгілейік.
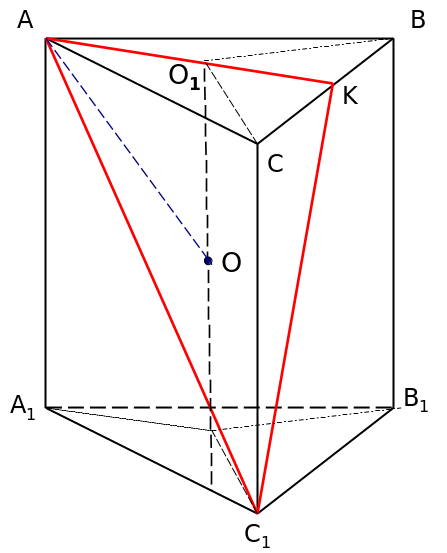
1) ΔАСК үшбұрышын қарасырайық: СК=а/2, АС=а
АК=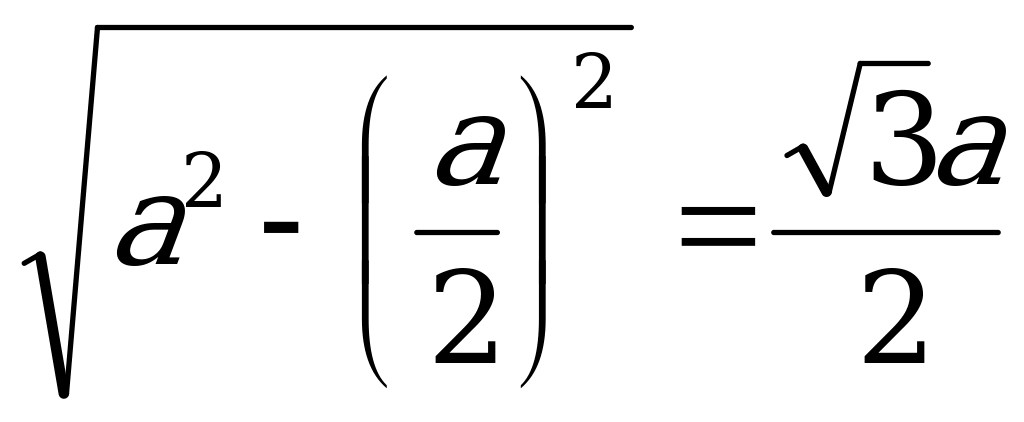
2) ΔАКС1 – тең бүйірлі, тікбұрышты үшбұрыш
1= 1К =45º
АК=КС1=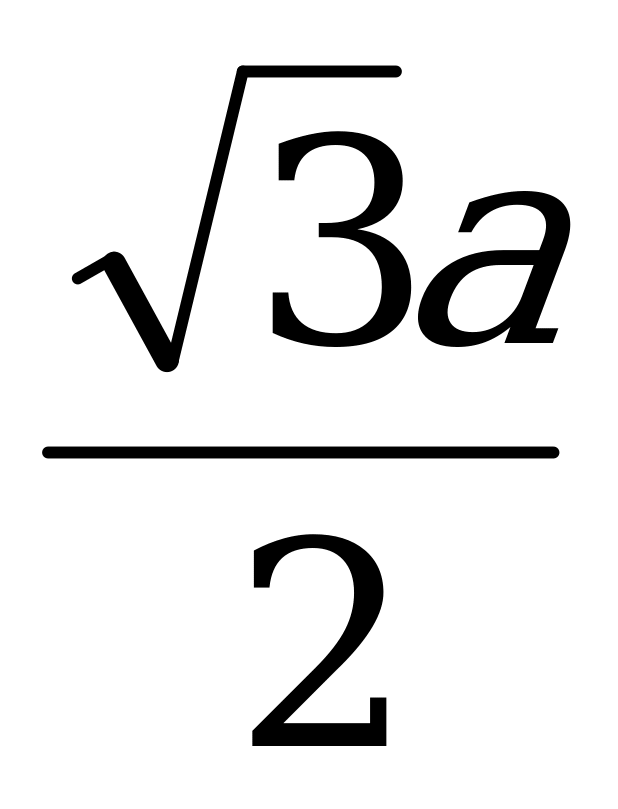
АС1=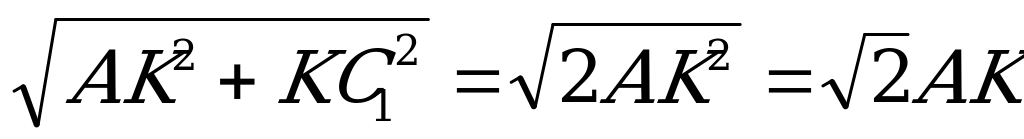 (Пифагор теоремасы)
(Пифагор теоремасы)
АС1=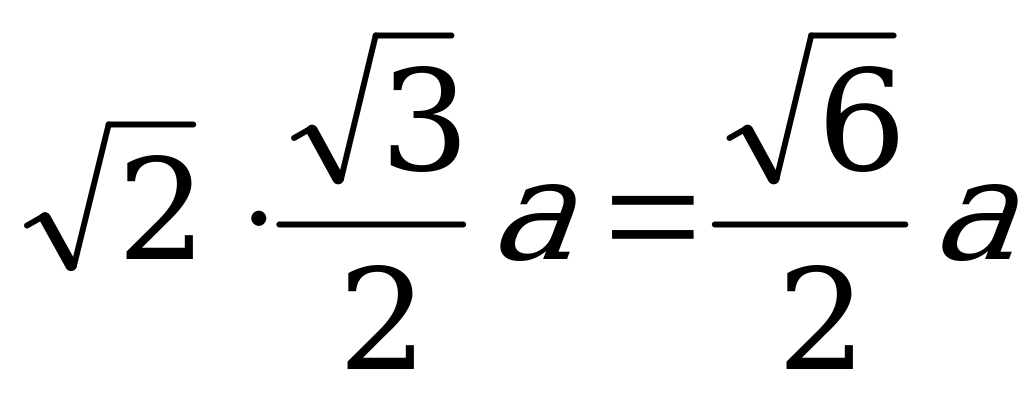
АС1=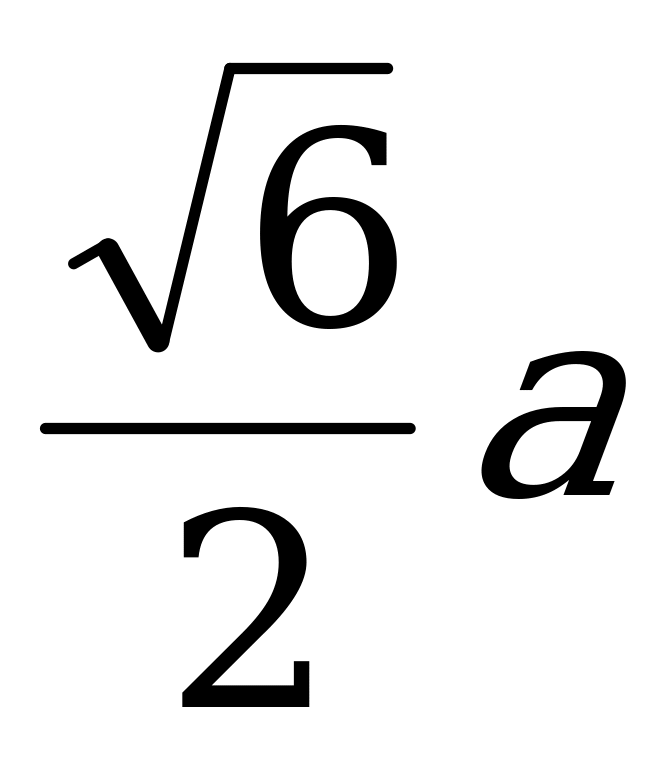
3) ΔАА1С1 –тікбұрышты үшбұрыш
АА1=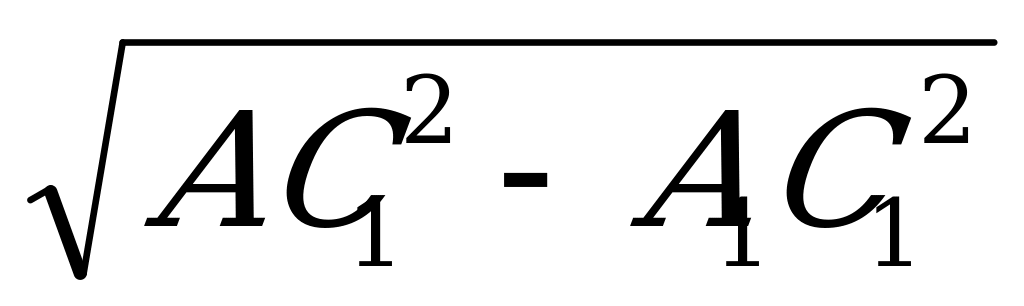
АА1=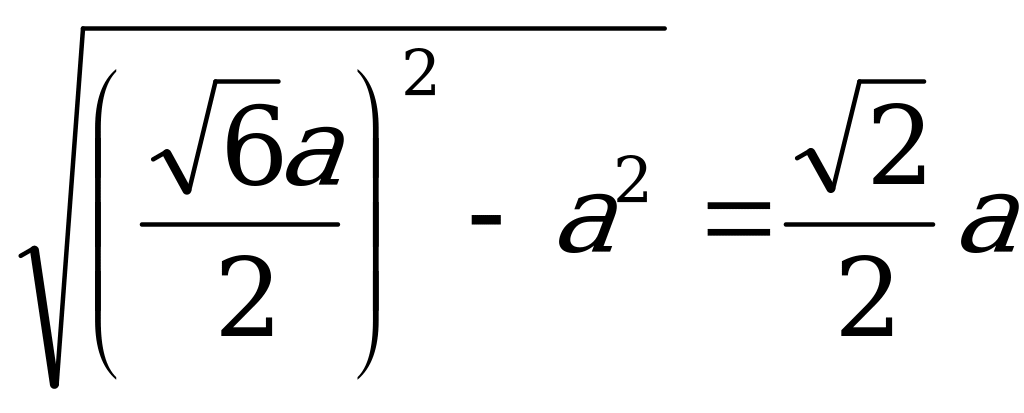
АА1=H
Н=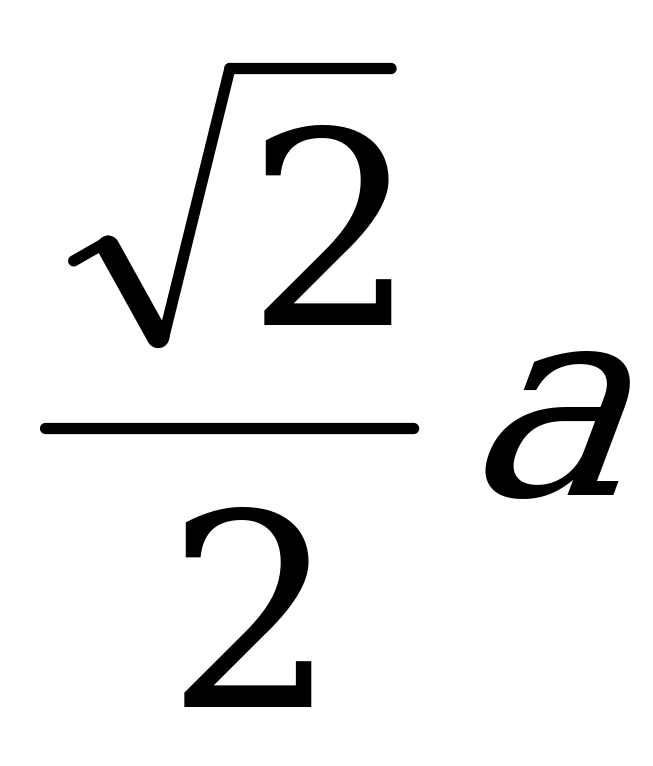
4) ОО1= ½*Н
ОО1= 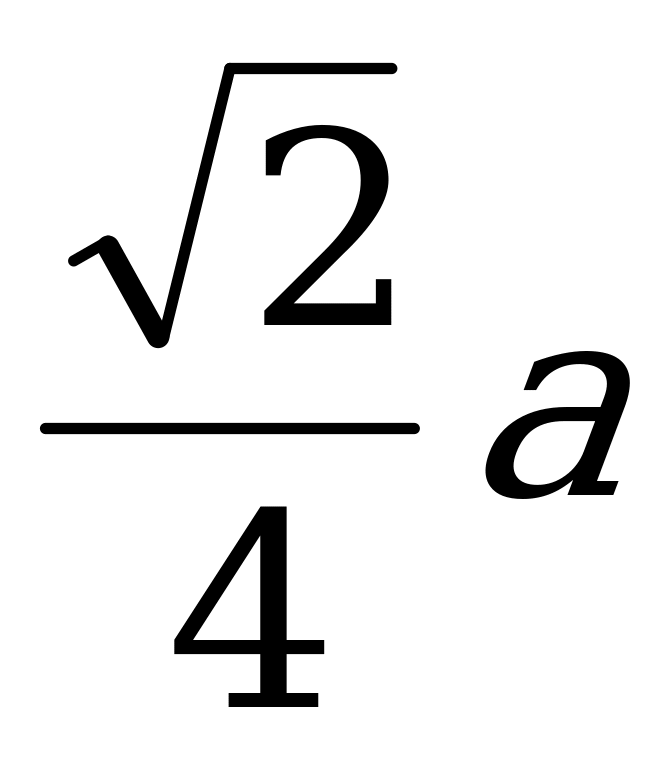
5) ΔАОО1 –тікбұрышты үшбұрыш:
АО1=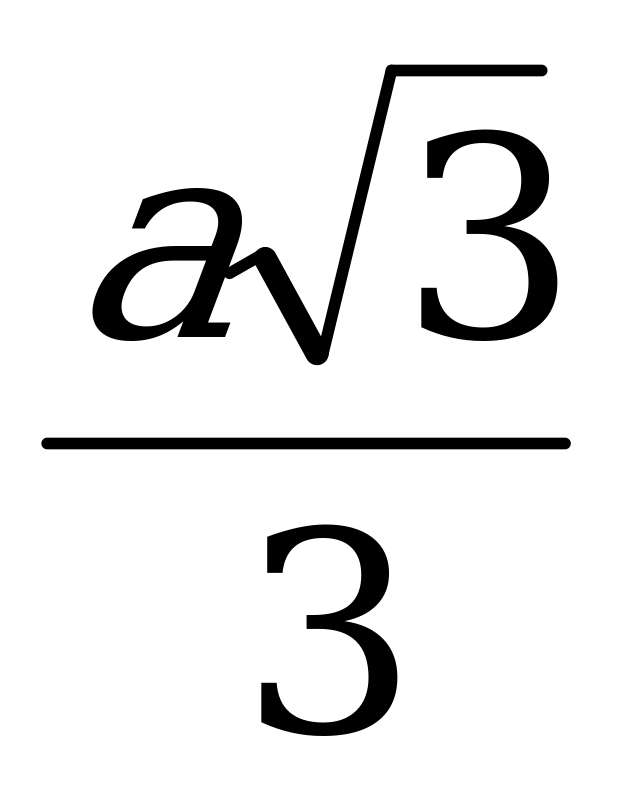 (үшбұрышқа сырттай сызылған шеңбер радиусы)
(үшбұрышқа сырттай сызылған шеңбер радиусы)
АО =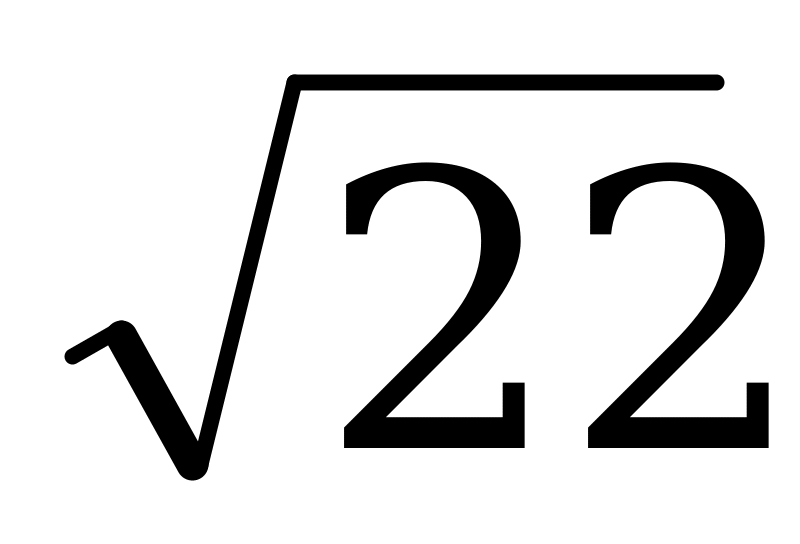 ,
,
АО2= ОО12 + АО12
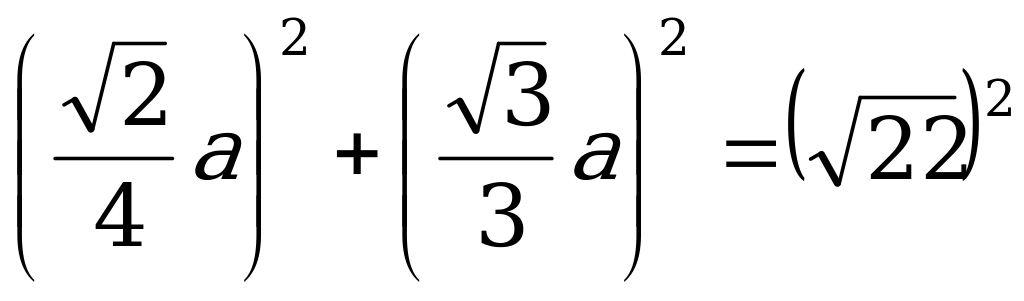
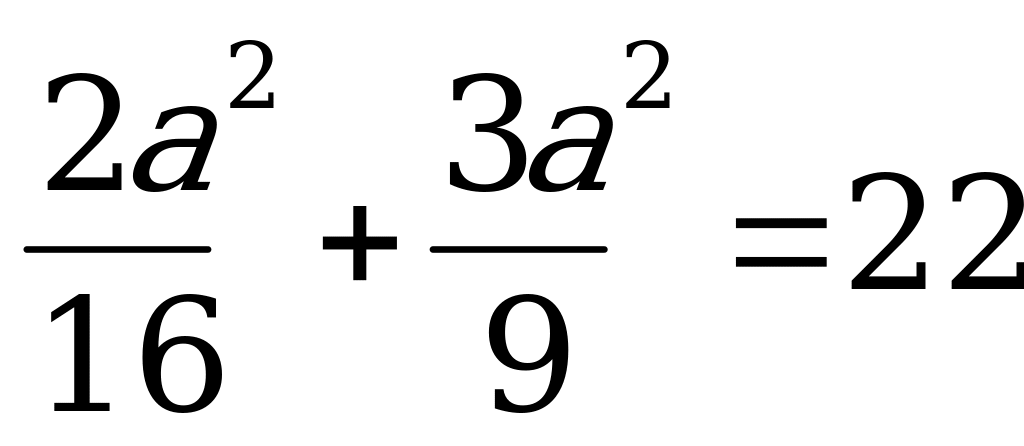
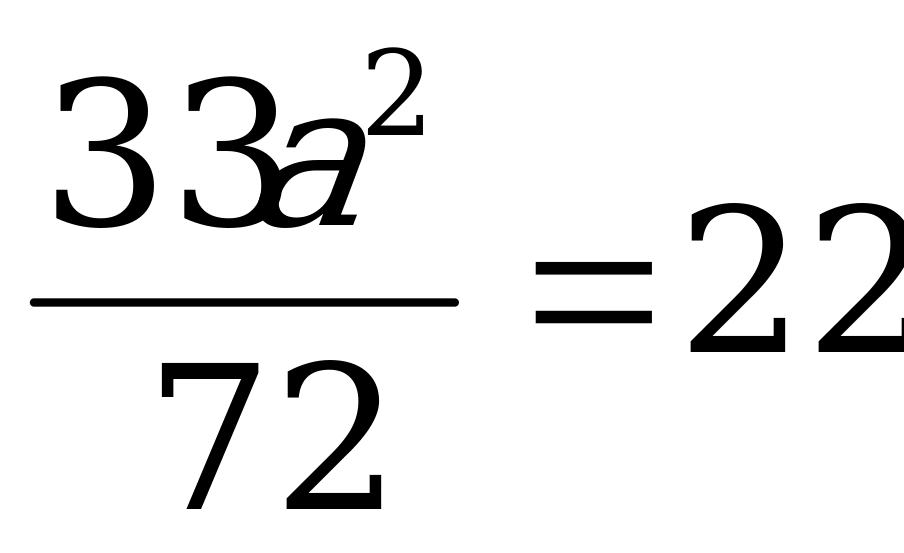
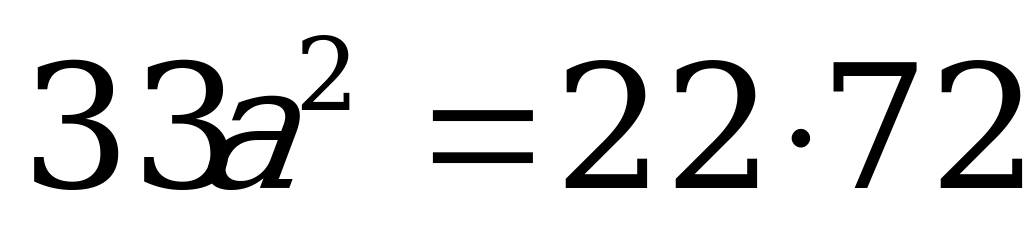
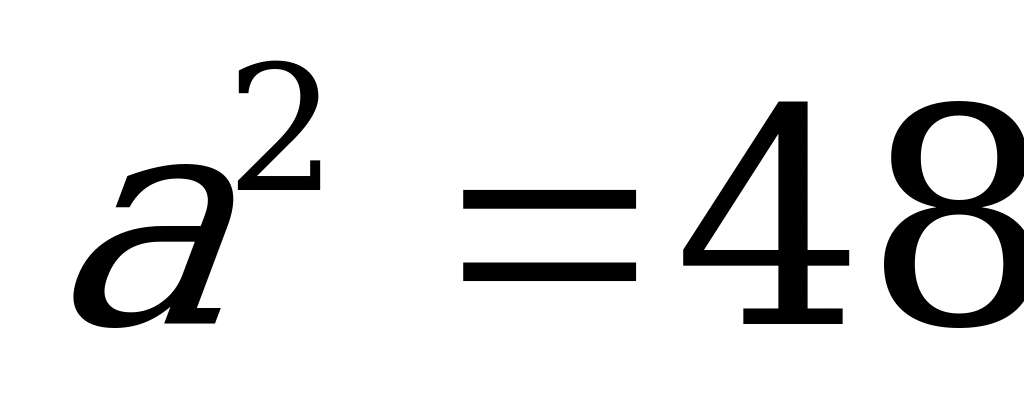
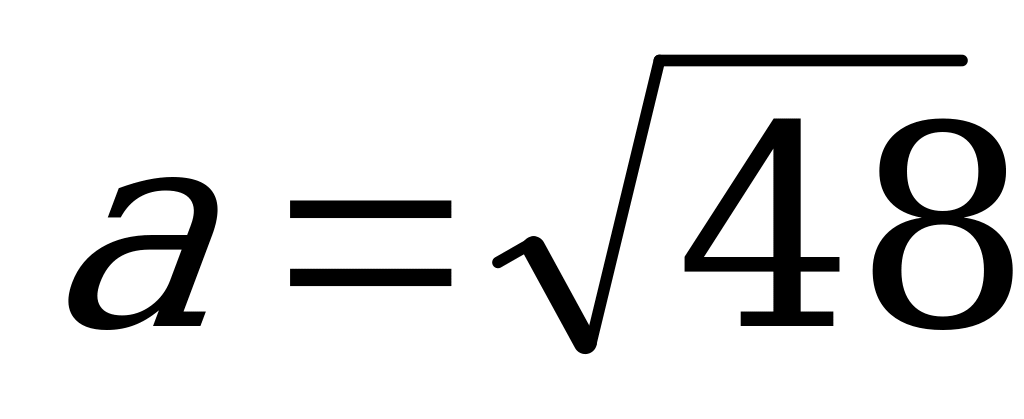
6) Н=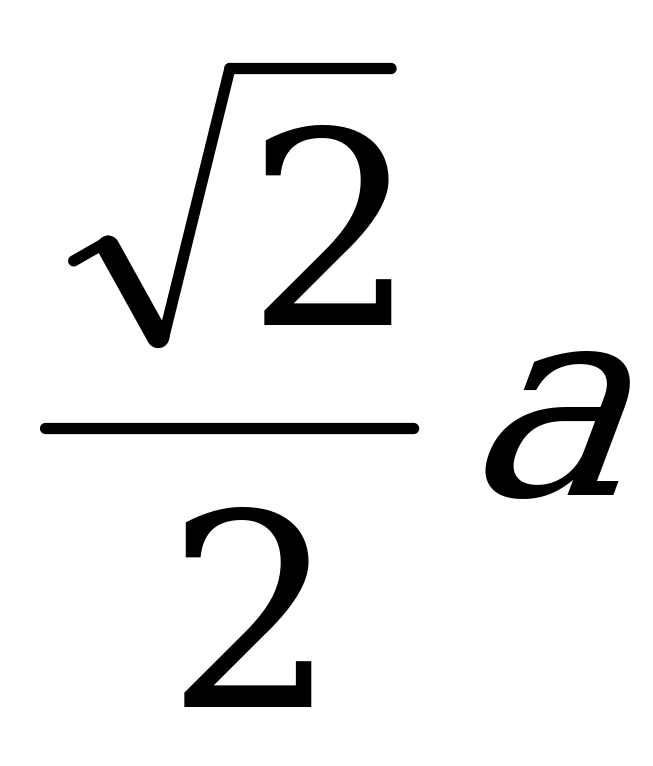 теңдігіне а-ның мәнін қойямыз.
теңдігіне а-ның мәнін қойямыз.
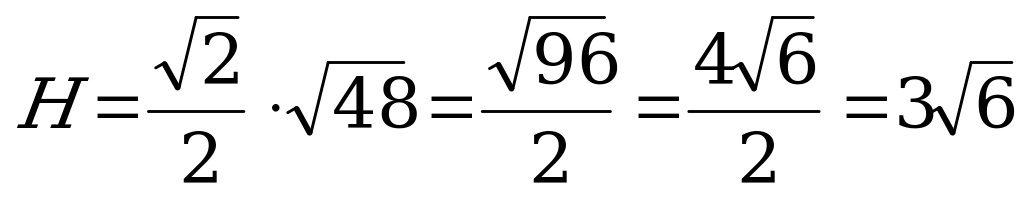
Н=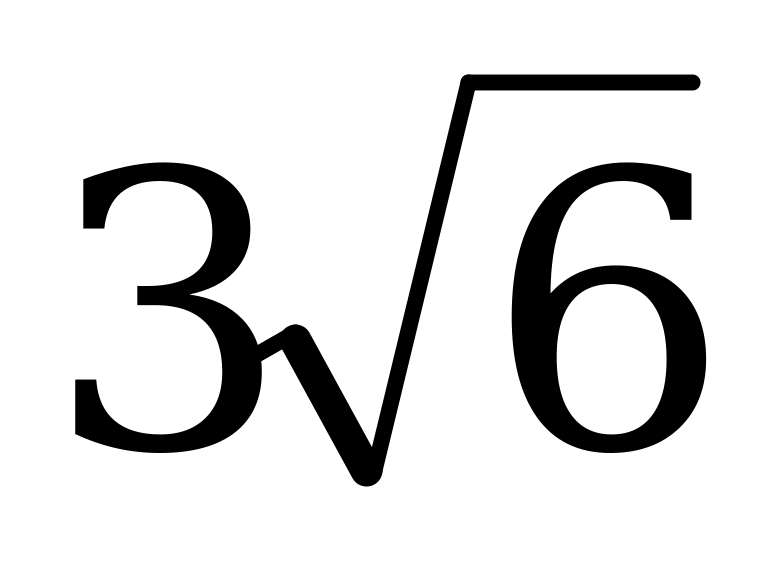
7) Енді призманың көлемін табамыз: 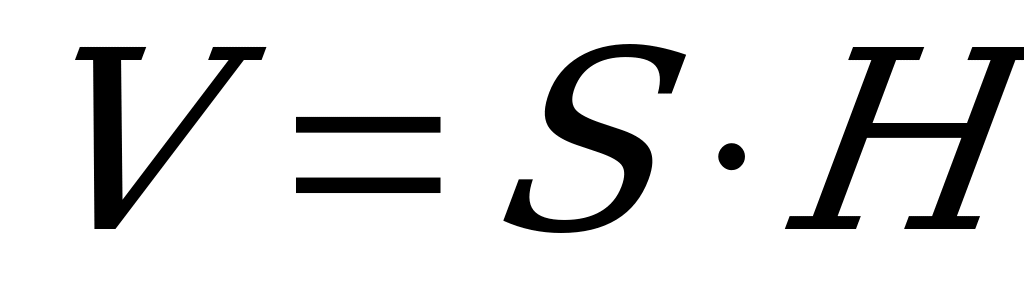
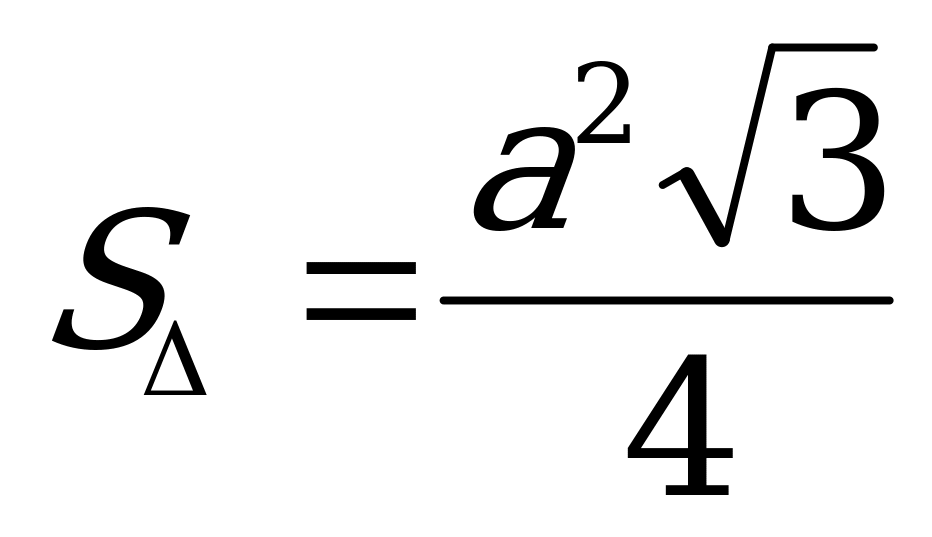
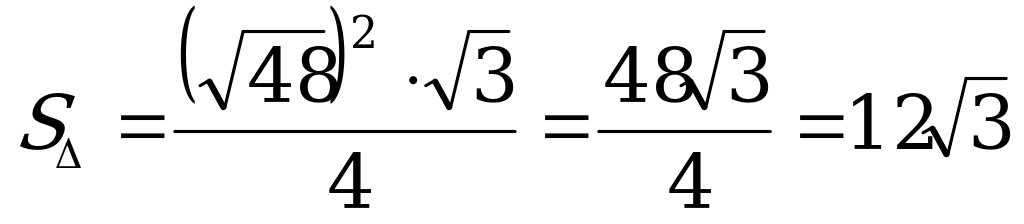
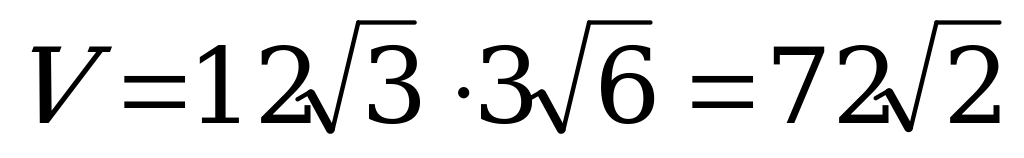
Жауабы: 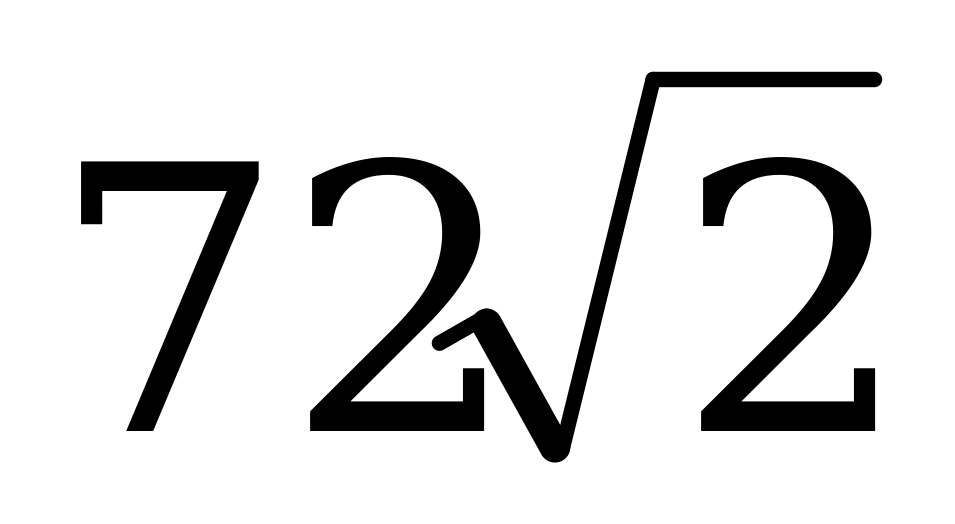
8.Үшбұрышты пирамиданың екі бүйір жағы өзара перпендикуляр және олардың
аудандары Р мен Q-ға тең, ал ортақ қырының ұзындығы а-ға тең.
Пирамиданың көлемін тап.
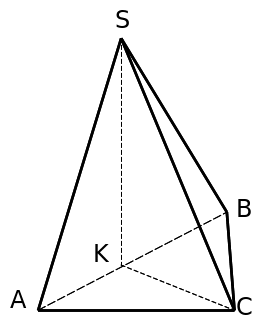
Шешуі: Есеп шарты бойынша АВ=а
SΔSАВ =Р және SΔАВС =Q
(ΔSАВ)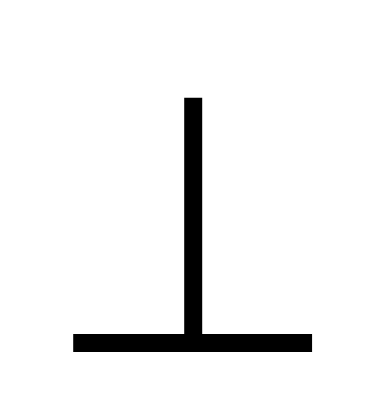 (ΔАВС). Сонда SК – пирамида биіктігі болады
(ΔАВС). Сонда SК – пирамида биіктігі болады
Пирамиданың көлемі: 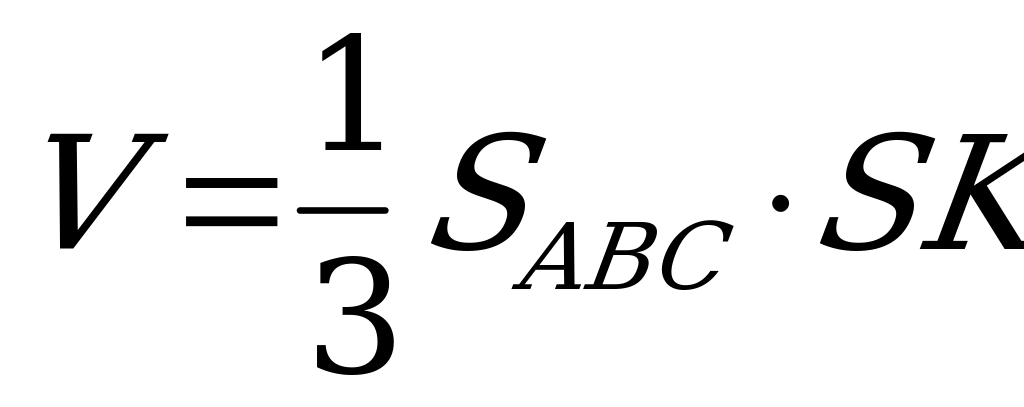
1)Алдымен, ΔSАВ-ны қарастырамыз
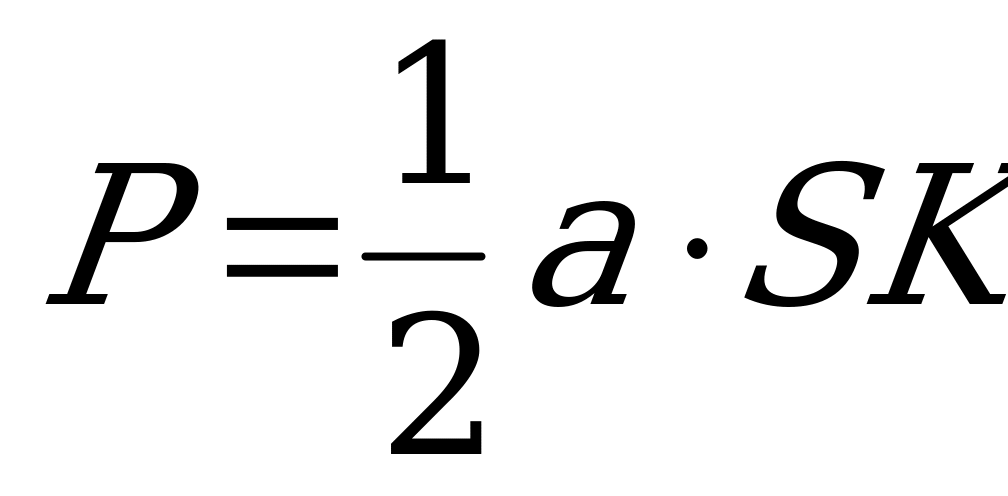
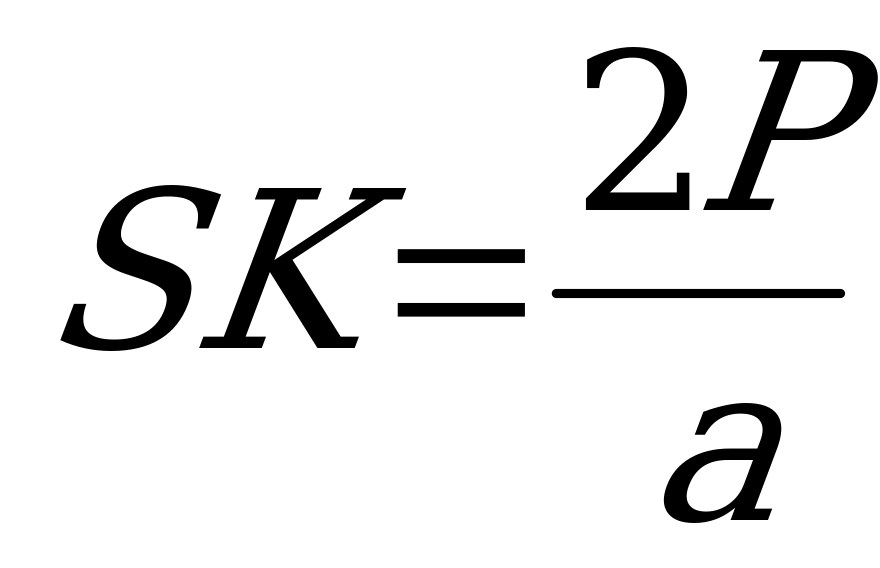
2) 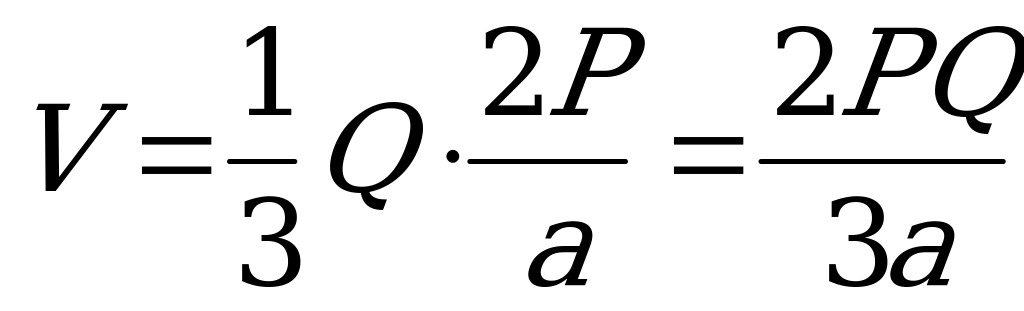
Жауабы: 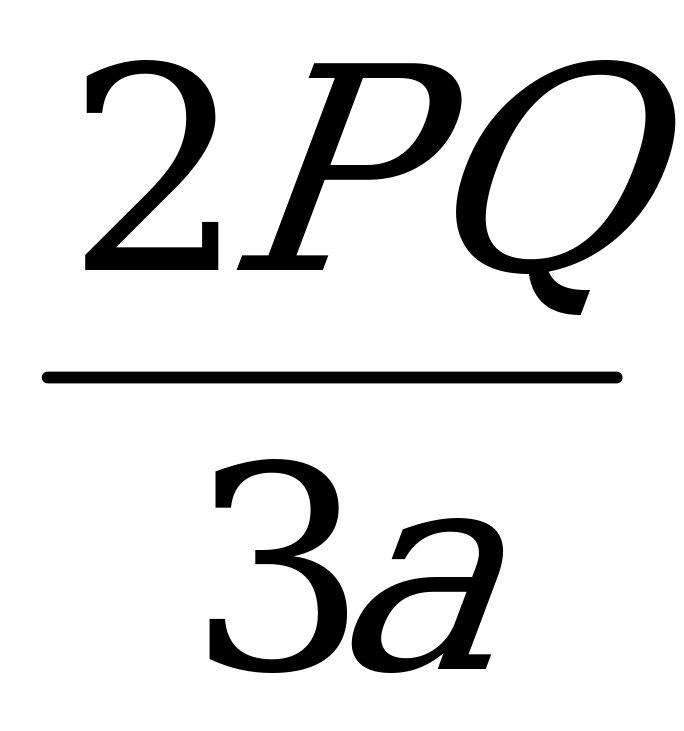









 ерілгені: пирамида, шар
ерілгені: пирамида, шар 1В=
1В=

 В12= АО2 – ОО12
В12= АО2 – ОО12