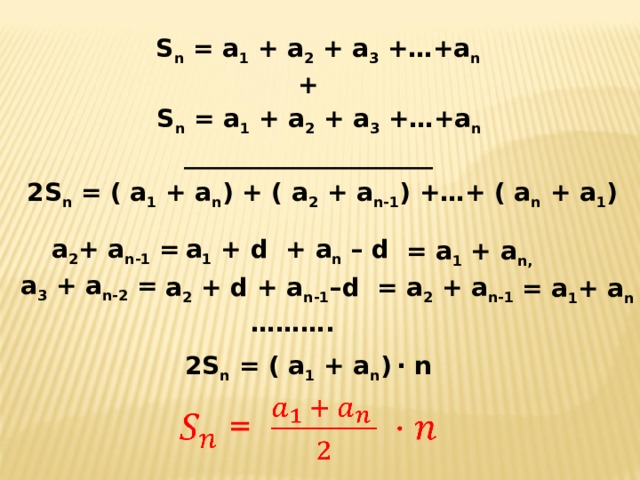Россия, Советск Калининградской области
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 24.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 20.05.2025 13:04
Кузьмина Елена Анатольевна
учитель математики
64 года
981
58 769 
Местоположение
Специализация
Сумма n-первых членов арифметической прогрессии
Категория:
Алгебра
25.01.2021 15:47
Просмотр содержимого документа
«Сумма n-первых членов арифметической прогрессии»
«О, сколько нам открытий
чудных …
Готовит просвещенья дух,
И опыт – сын ошибок трудных,
И гений – парадоксов друг»
А.С. Пушкин
Папирус Ахмеса
Древний Египет, страна великих достижений человеческой мысли, великих астрономов и математиков.
Самый большой, сохранившийся до наших дней, древнеегипетский математический текст – это папирус писца XVIII – XVII веков до нашей эры Ахмеса. Он имеет размер 5,25 м на 33 см, содержит 84 задачи
Задача из папируса Ахмеса
Если камушки (или другие предметы) разложить рядами в форме треугольника так, что в первом ряду положить 1 камень, во втором – 2 и т.д., то их количество называли «треугольным числом».
Таким образом, треугольные числа образуют такую последовательность:
а 1 =1, а 2 =2, а 3 =3, а 4 =4, …..,
а сумма этих камушков образует треугольное число.
Треугольное число - это и есть сумма n -первых членов арифметической прогрессии.
Обозначим его
S n = 1 + 2 + 3 + 4 + 5 + …… + n
Дано: а n – арифметическая прогрессия,
а 1 =1, а 2 =2, а 3 =3, а 4 =4, …..
Найти: S 100 .
Решение:
S 100 = 1 + 2 + 3 + 4 + …….. +100
+
S 100 = 100 + 99 + 98 +97+ ………. + 1
2 S 100 =10 1 + 101 + 101 + 101 + …..+ 101
100 раз
2 S 100 = 101 * 100
S 100 = 5050
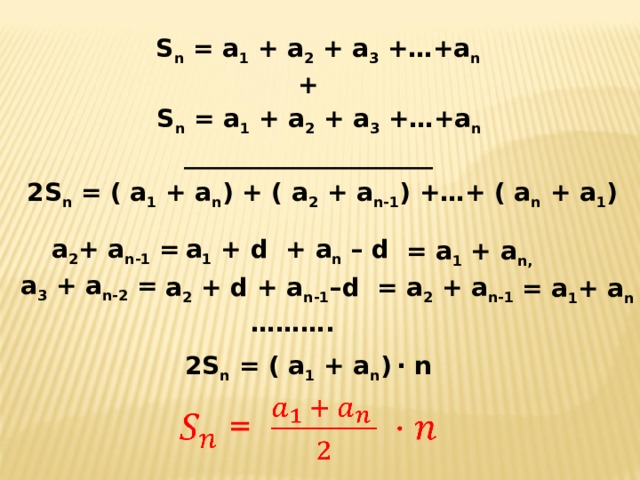
S n = а 1 + а 2 + а 3 +…+а n
+
S n = а 1 + а 2 + а 3 +…+а n
____________________
2 S n = ( а 1 + а n ) + ( а 2 + а n -1 ) +…+ ( а n + а 1 )
а 2 + а n -1 =
а 1 + d
+ a n – d
= а 1 + a n ,
а 3 + а n-2 =
a 2 + d + a n-1 –d
= a 2 + a n-1
= a 1 + a n
……… .
2S n = ( a 1 + а n ) · n
Если а n – арифметическая прогрессия,
а 1 =1, а 2 =2, а 3 =3, а 4 =4, …..
то
Если подставить а n = а 1 + d ( n-1)
а) а 1 = 2, а 10 = 20. S 10 =
110
б) а 1 = -5, а 7 = 1. S 7 =
-14
-57
в) а 1 = -2, а 6 = -17. S 6 =
0
г) а 1 = -5, а 11 = 5. S 11 =
д) Дано: (а n ) –арифметическая прогрессия;
а 1 =3, а 60 = 57
Найти: S 60
Ответ: 1800 .
Вычислите сумму девяти первых членов арифметической прогрессии (в n ), если в 1 = -17, d = 6
Можно ли вычислить сумму сразу, используя формулу?
Вопрос. А нельзя ли найти сумму, не вычисляя девятого члена прогрессии?
Запишите и запомните!
- Вычислите сумму девяти первых членов арифметической прогрессии (в n ), если в 1 = -17, d = 6
2. а 1 = 3, d = 4. S 4 = ?
3. а 1 = 2, d = -5. S 3 = ?
Вариант 1
Дано: (а n ) – арифметическая прогрессия.
- а 1 = -3, а 6 = 21. S 6 = ?
- а 1 = 6, d = -3. S 4 = ?
Вариант 2
Дано: (а n ) – арифметическая прогрессия.
- а 1 = 2, а 8 = -23. S 8 = ?
- а 1 = -7, d = 4. S 5 = ?
Проверка
Вариант 1
Вариант 2
Спасибо за внимание!
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
Закрыть через 5 секунд
