Россия, Новомосковск
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 16.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 24.05.2023 13:52
Поспелова Галина Васильевна
Учитель информатики
72 года
3 122
18 645 
Местоположение
Специализация
Таблицы истинности
Категория:
Информатика
03.03.2022 19:45
Просмотр содержимого документа
«Таблицы истинности»
Работу выполнила Поспелова Г. В.,
учитель информатики
МБОУ «СОШ №20»
г. Новомосковска
Составить таблицу истинности
F = (AvB)&(ĀvB)
A
0
B
0
0
Ā
AvB
1
1
ĀvB
0
1
(AvB)&(ĀvB)
1
1. Количество входных переменных в заданном выражении равно двум (A,B) . Значит, количество входных наборов, а значит и строк Q=2 2 =4
2. Количество столбцов равно 6 (2 переменные + 4 операции).
Проверим
A
B
0
0
0
Ā
AvB
1
1
1
ĀvB
1
0
1
0
(AvB)&(ĀvB)
1
0
A
0
B
0
Ā
0
1
1
1
AvB
1
0
1
ĀvB
0
1
(AvB)&(ĀvB)
1
0
0
1
1
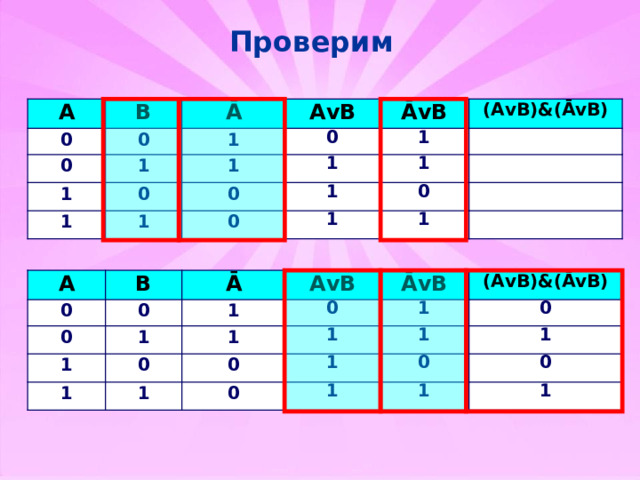
Проверим
A
B
0
0
Ā
0
AvB
1
1
1
ĀvB
0
0
1
1
1
(AvB)&(ĀvB)
0
1
1
1
1
0
0
1
1
A
0
B
0
Ā
0
1
1
AvB
1
1
1
0
ĀvB
0
1
1
(AvB)&(ĀvB)
1
0
1
0
1
0
1
1
0
1
0
1
Составить таблицу истинности
для логической функции:
F =Ā& (BvC)
- Количество входных переменных в заданном выражении равно трем (A,B,C) . Значит, количество входных наборов, а значит и строк Q=2 3 =8 .
- Количество столбцов равно 6 (3 переменные + 3 операции).
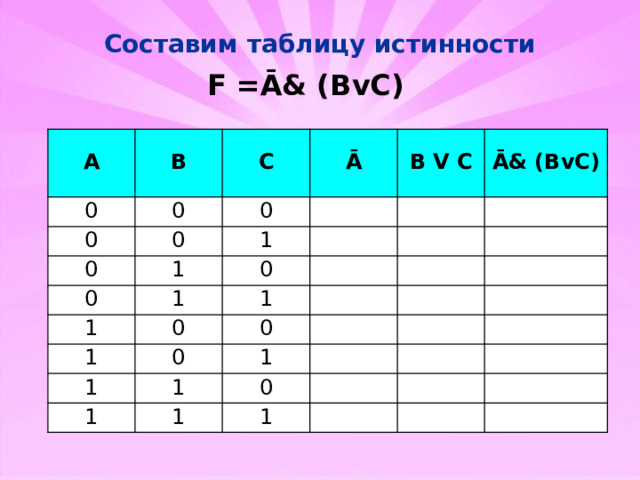
Составим таблицу истинности
F =Ā& (BvC)
A
0
B
0
C
0
Ā
0
0
0
1
B V C
1
0
1
0
1
Ā& (BvC)
0
1
1
0
0
1
1
1
1
0
1
1
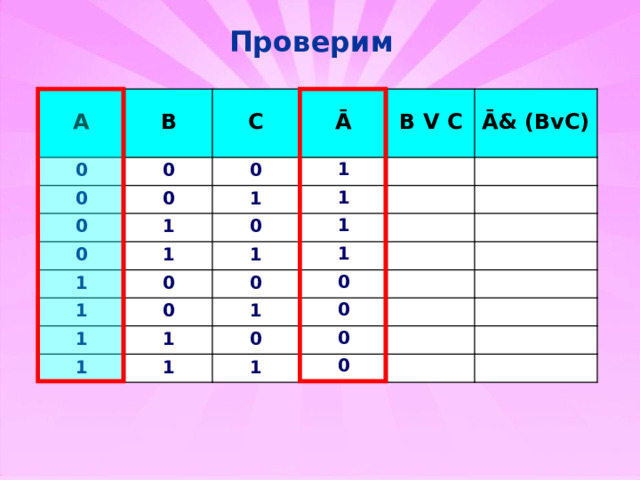
Проверим
A
0
B
C
0
0
Ā
0
0
0
B V C
1
1
1
0
0
1
Ā& (BvC)
1
1
1
1
1
0
0
1
1
0
0
1
1
1
0
0
1
0
1
0
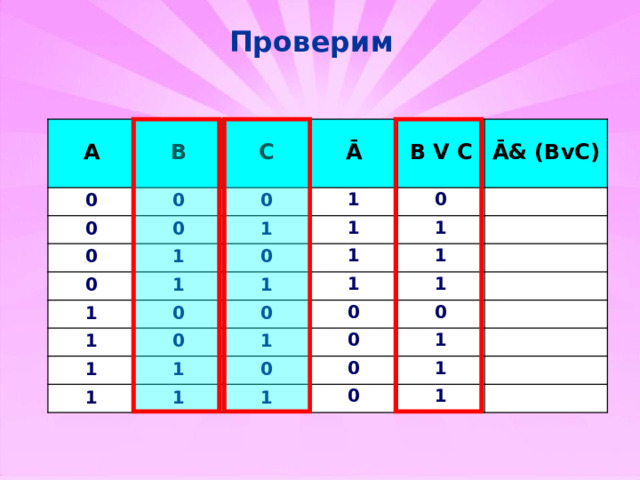
Проверим
A
B
0
0
0
C
0
0
Ā
0
1
1
1
0
B V C
0
1
1
Ā& (BvC)
0
1
1
0
1
1
1
1
1
0
1
0
1
0
1
1
1
0
0
0
1
0
1
1
1
0
1
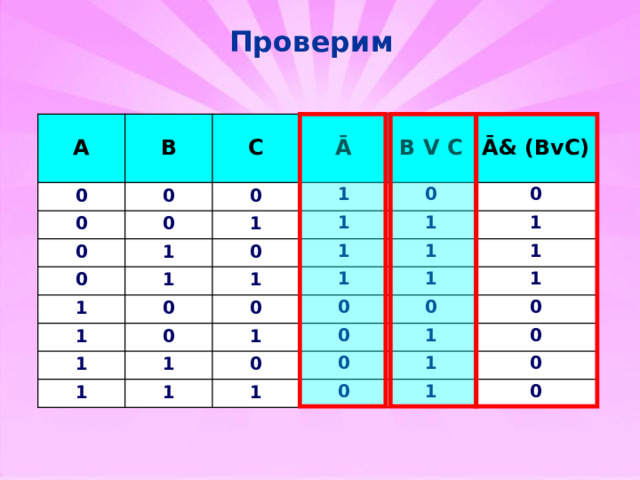
Проверим
A
0
B
0
C
0
Ā
0
0
0
1
1
0
1
B V C
1
0
0
1
Ā& (BvC)
1
0
0
1
1
1
1
1
0
1
0
1
1
0
1
1
1
1
1
0
1
1
0
0
0
0
1
1
0
1
0
0
1
0
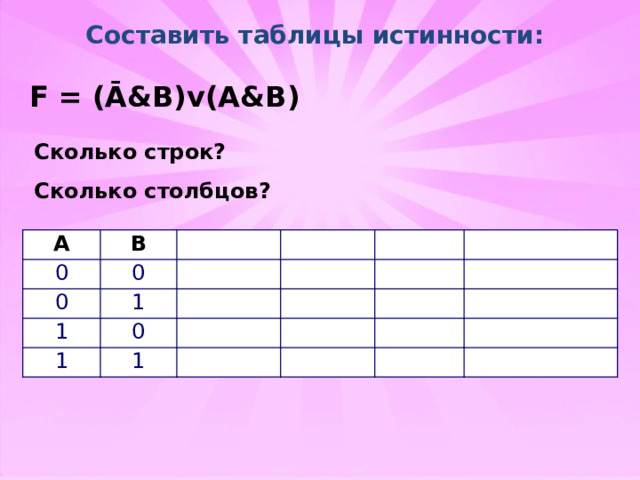
Составить таблицы истинности:
F = (Ā&B)v(A&B)
Сколько строк?
Сколько столбцов?
A
0
B
0
0
1
1
1
0
1
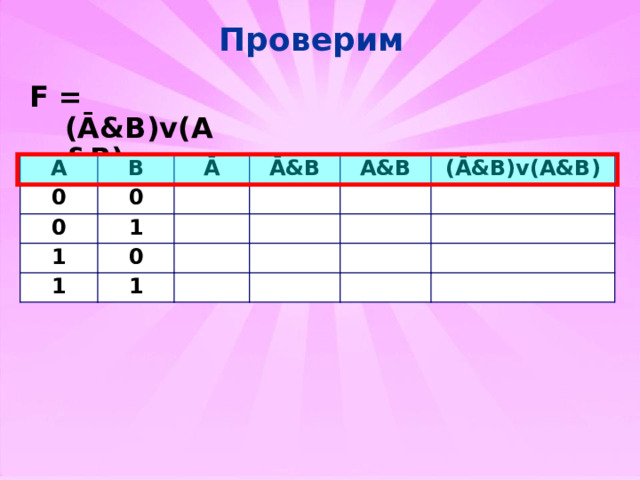
Проверим
F = (Ā&B)v(A&B)
A
0
B
0
0
Ā
1
1
Ā&B
0
A&B
1
(Ā&B)v(A&B)
1
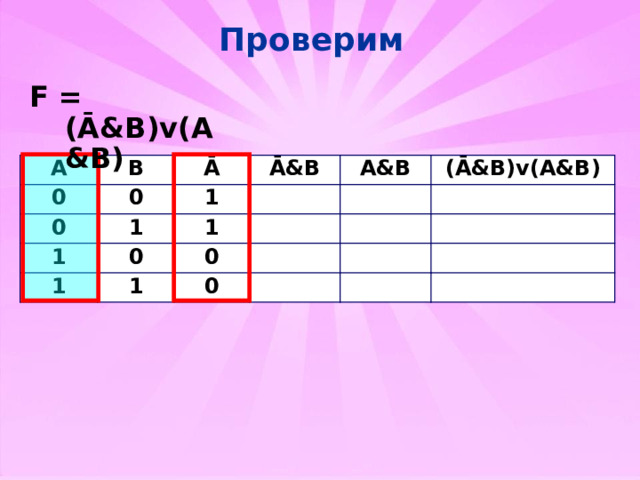
Проверим
F = (Ā&B)v(A&B)
A
0
B
0
Ā
0
Ā&B
1
1
1
0
1
1
A&B
1
0
(Ā&B)v(A&B)
0
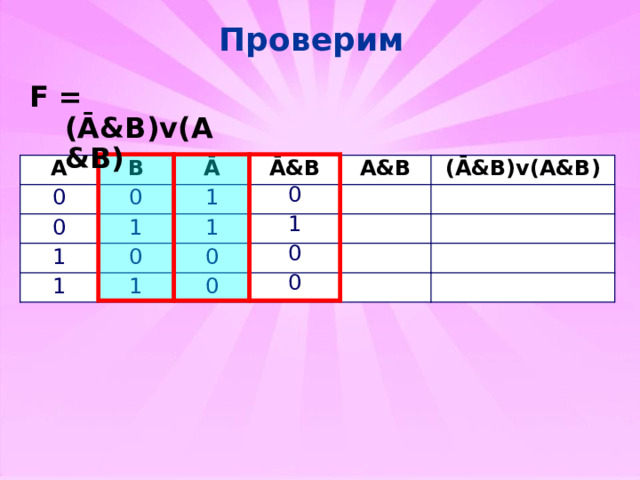
Проверим
F = (Ā&B)v(A&B)
A
B
0
0
Ā
0
1
1
1
Ā&B
0
0
1
1
A&B
1
0
1
(Ā&B)v(A&B)
0
0
0
Проверим
F = (Ā&B)v(A&B)
A
0
B
0
0
Ā
1
1
Ā&B
1
0
0
1
A&B
1
(Ā&B)v(A&B)
1
0
0
1
0
0
0
0
0
1
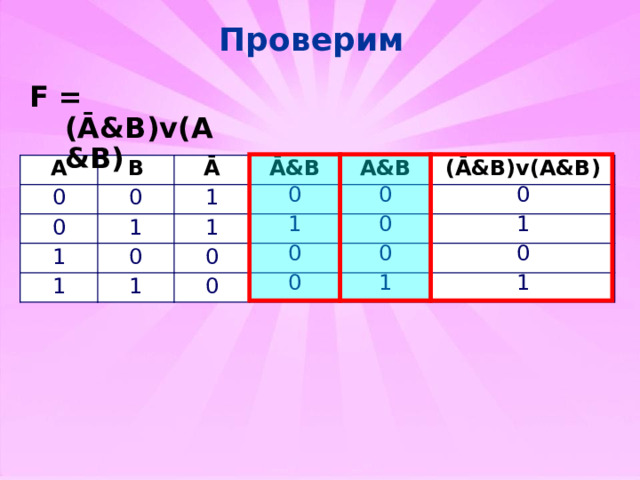
Проверим
F = (Ā&B)v(A&B)
A
0
B
0
0
Ā
1
1
Ā&B
1
0
0
1
A&B
1
1
1
0
0
(Ā&B)v(A&B)
0
0
0
0
0
0
1
0
1
1
Составить таблицы истинности:
F = (AvB)v((Ā&C)vB)
Сколько строк?
Сколько столбцов?
A
B
0
0
C
0
0
0
0
1
1
0
1
1
0
0
1
1
0
0
1
1
1
1
0
1
1
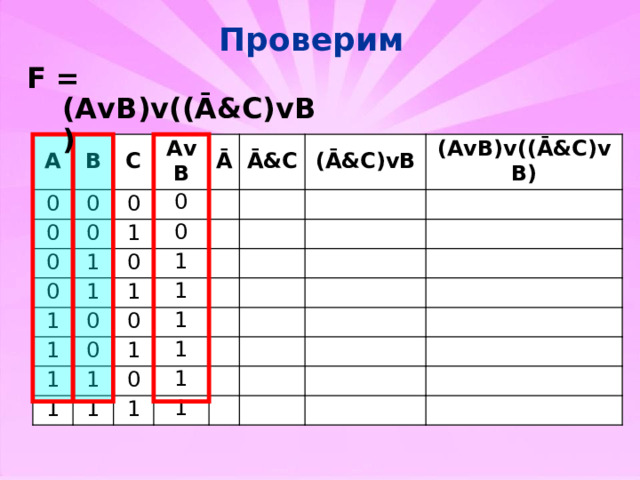
Проверим
F = (AvB)v((Ā&C)vB)
A
B
0
0
0
C
0
0
0
AvB
0
1
0
Ā
1
0
1
Ā&C
0
1
1
0
( Ā&C)vB
1
1
0
1
0
(AvB)v((Ā&C)vB)
1
1
1
1
1
1
0
1
1
1
1
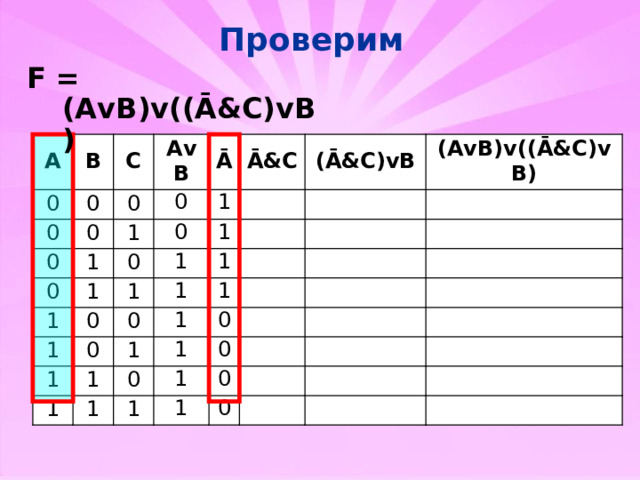
Проверим
F = (AvB)v((Ā&C)vB)
A
B
0
0
C
0
0
AvB
0
0
0
1
0
1
Ā
Ā&C
1
1
1
0
0
1
0
1
1
( Ā&C)vB
1
1
(AvB)v((Ā&C)vB)
1
1
0
0
1
1
1
1
1
1
1
0
0
1
1
0
0
1
0
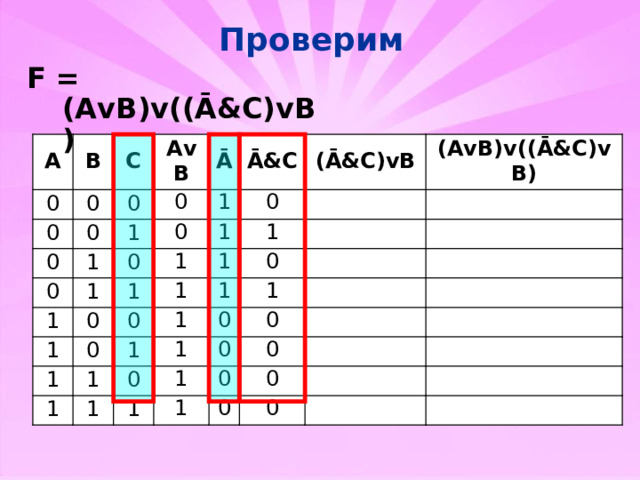
Проверим
F = (AvB)v((Ā&C)vB)
A
B
0
0
C
0
0
0
AvB
0
0
1
Ā
0
1
1
Ā&C
1
0
0
1
1
0
0
1
( Ā&C)vB
1
1
(AvB)v((Ā&C)vB)
0
1
0
1
1
1
1
0
1
1
1
1
1
1
1
0
0
1
0
1
0
0
0
1
0
0
0
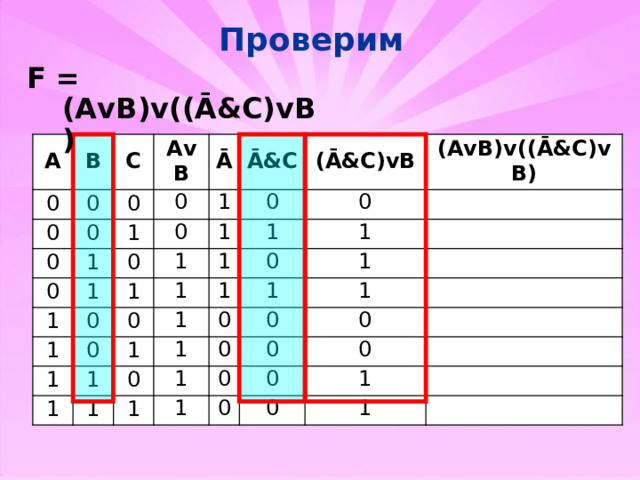
Проверим
F = (AvB)v((Ā&C)vB)
A
B
0
0
C
0
0
0
0
AvB
0
1
0
1
Ā
1
0
0
Ā&C
1
1
1
0
0
1
( Ā&C)vB
1
1
1
0
1
1
0
1
0
(AvB)v((Ā&C)vB)
1
1
0
1
1
1
1
1
1
0
1
0
1
1
0
1
0
1
0
1
0
0
0
0
0
0
1
1
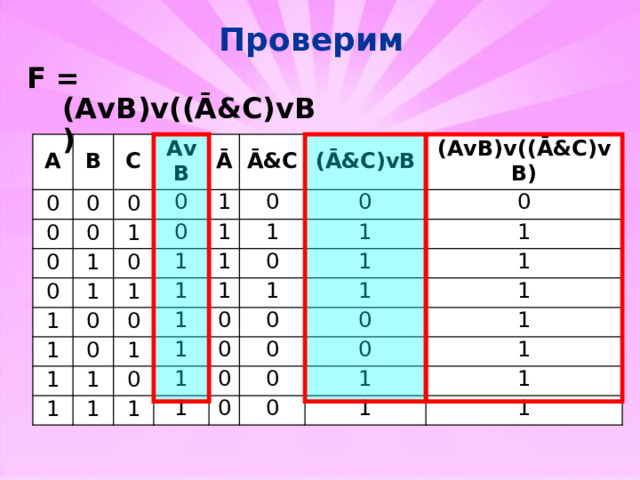
Проверим
F = (AvB)v((Ā&C)vB)
A
B
0
0
C
0
0
AvB
0
0
0
1
1
0
Ā
1
0
1
Ā&C
0
1
0
1
0
1
1
( Ā&C)vB
1
0
0
1
1
0
(AvB)v((Ā&C)vB)
1
1
1
1
0
0
1
1
1
1
1
0
1
0
1
1
1
1
1
0
1
1
0
0
0
1
0
1
0
1
0
0
1
1
0
1
1
1
Босова Л.Л. Информатика и ИКТ : учебник для 9 класса : в 2 ч. Ч. 1 / Л.Л. Босова, А.Ю. Босова. – М. : БИНОМ. Лаборатория знаний, 2012.-244с.
Фон слайдов
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
Закрыть через 5 секунд
