Муниципальное казённое общеобразовательное учреждение
«Беляевская средняя общеобразовательная школа»
Технологическая карта
урока по алгебре в 8 классе
по теме «Рациональные уравнения как математические модели реальных ситуаций»
Разработала:
Алымова Лилия Владимировна
учитель математики первой
квалификационной категории
Раздел Квадратные уравнения
Тема урока Рациональные уравнения как математические модели реальных ситуаций
Количество часов на изучение темы – 6, урок 3
Тип урока (типология уроков в дидактической системе деятельностного метода) – урок рефлексии и отработки знаний
Цели урока
Деятельностная: формирование способностей к фиксированию собственных затруднений, выявлению их причин и коррекции собственных действий.
Содержательная: совершенствование умений решения задач с помощью рациональных уравнений.
Развивающая: создание условий для приобретения первоначального опыта математического моделирования, развития интереса к математическому творчеству, развития мышления (умения анализировать, сравнивать, строить аналогии), формирования общеучебных умений.
Воспитательная: воспитание познавательного интереса к математике, ответственности и осмысленной учебной деятельности, коммуникативного умения сотрудничать с одноклассниками и учителем.
Методическая: самоанализ урока при реализации системно-деятельностного подхода на уроках математики в условиях ФГОС.
Планируемые результаты, в том числе УУД
Предметные: формировать умения решать текстовые задачи на производительность с помощью рациональных уравнений, реализовывая все этапы математического моделирования.
Метапредметные: уметь использовать таблицы для интерпретации информации, понимать сущность алгоритма и уметь действовать в соответствии с алгоритмом, уметь самостоятельно ставить учебные цели, рассуждать по аналогии, делать аргументированные выводы.
Познавательные УУД: уметь выделять необходимую информацию из текстов задач, владеть общим приемом решения задач, переводить словесные формулировки на математический язык, описывать реальные ситуации с помощью математических моделей (уравнений), планировать ход решения задачи, применять алгоритмы решения уравнений, выполнять алгебраические преобразования при решении уравнений, обнаруживать и устранять ошибки арифметического, алгебраического и логического характера.
Личностные УУД: прививать интерес к предмету путём решения задач, связанных с жизненной деятельностью человека; проявлять внимание; оценивать собственную учебную деятельность; устанавливать связь между целью деятельности и ее результатом, формировать адекватную самооценку.
Коммуникативные УУД: воспринимать текст с учетом поставленной учебной задачи, находить в тексте необходимую информацию; слушать и понимать речь других; планировать учебное сотрудничество с учителем и сверстниками; осуществлять самоконтроль; организовывать учебное взаимодействие в группе.
Регулятивные УУД: отвечать на вопросы; определять и формулировать цель деятельности на уроке; удерживать цель деятельности до получения ее результата; планировать свои действия; оценивать уровень владения учебным действием (отвечать на вопрос «что я не знаю и не умею?»); осознавать качество и уровень усвоения материала.
Основные понятия темы
Рациональные, квадратные, дробно-рациональные уравнения; математическая модель задачи.
Методы и формы организации деятельности: фронтальная и индивидуальная работа, выполнение тестовых заданий, коллективная работа и в парах, самостоятельная работа.
Ресурсы: УМК «Алгебра 8» А.Г. Мерзляка, мультимедийный проектор и презентация, конверты с задачами и карточками-подсказками, карточки с нестандартными задачами, маршрутные листы с фиксированием результатов деятельности
Технологическая карта урока
| № | Этап урока | Деятельность учителя | Деятельность обучающегося | Время | Формируемые УУД |
| Познавательные | Регулятивные | Коммуникативные | Личностные |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | Этап мотивации (самоопределения) к коррекционной деятельнос-ти. | Приветствие учащихся; проверка учителем готовности класса к уроку; проверка готовности учащихся к уроку; организация внимания; знакомство с планом урока. | Быстрое включение класса в деловой ритм; знакомство с планом урока; организация внимания. | 1 | Осознанное и произвольное построение речевого высказывания. | Прогнозирова-ние своей деятельности. | Умение слушать и вступать в диалог. | Умение выделять нравственный аспект поведения. |
| 2 | Этап фиксации затруднений в деятель-ности. | -Дома вы выполняли индивидуальные задания, выбранные из 6 на прошлом уроке. На столе 6 листов с высказываниями известных учёных о математике. Будем работать на уроке под номером того девиза, который номер выполнен вами верно,без малейшей ошибки. -Выявление факта выполнения д/з всем классом. -Выяснение причин невыполнения д/з отдельными учениками и принятие мер. -Определение типичных недостатков в знаниях и причин их появления. -Исправление ошибок, допущенных учащимися в д/з. | -Проверка д/з. -Взаимопомощь и самоконтроль учащихся. | 3 | Ориентироваться в разнообразии способов решения задач. | Формировать способность к преодолению препятствий и самокоррекции, уметь выполнять самопроверку. | С достоинством признавать ошибки своего мнения (если они есть), корректировать их. | Формирование навыков самоанализа и самоконтроля. |
| 3. | Актуализа-ция знаний.
| Организует повторение, способствуя активизации памяти и внимания. 1) Назовите этапы решения задачи с помощью рационального уравнения. 2) Что является математической моделью задачи? 3) Какие уравнения называются рациональными? 4) 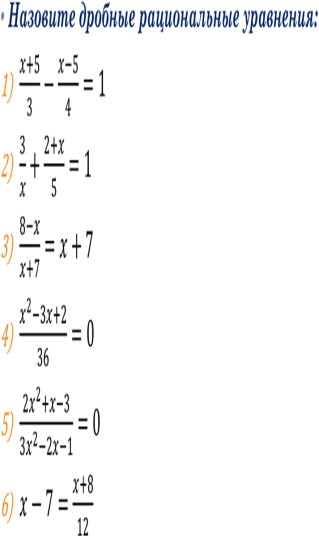 5) 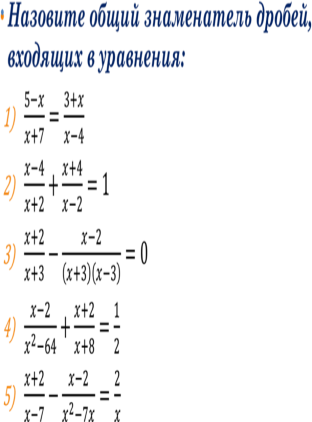 8) Сформулируйте алгоритм решения квадратного уравнения. 9) Сформулируйте алгоритм решения дробно-рационального уравнения. | Отвечают на вопросы | 5 | Актуализировать опорные знания и умения по основным способам решения квадратных, дробно-рациональных уравнений и задач, сводящихся к ним
| Определять последовательность действий. | Умение слушать и уважать отвечающего на вопрос. | Умение сконцентрировать внимание на достижение результата. |
| 4 | Подготовка учащихся к активному и сознательному усвоению нового материала. | -Проверяется решение задачи из д/з. Решение задач вызывает трудности у учащихся, т.к. дети не учитывают все этапы решения задач: 1.составление математической модели; 2. работа с составленной моделью; 3. ответ на вопрос задачи. -Сообщение темы изучения нового материала: «Рациональные уравнения как математические модели реальных ситуаций». -Формулировка вместе с учащимися целей данного урока: 1.изучит правила оформления задач, решающихся с помощью рациональных уравнений; 2.формировать умение решать и оформлять задачи. -Постановка учебной проблемы перед учащимися. Задача: Две бригады должны были изготовить по 180 книжных полок. Первая бригада в час изготовляла на 2 полки больше, чем вторая, и потому закончила работу на 3 ч раньше, чем первая. За сколько часов каждая бригада выполнила задание? | -Во время проверки д/з выявляют с помощью учителя полноту решения задачи.
- Записывают тему урока.
- Читают задачу
| 3 | Поиск и выделение необходимой информации. | Выстраивать последователь-ность необходимых действий (алгоритм действий). | Воспринимать текст с учётом поставленной учебной задачи и находить в тексте информацию, необходимую для решения. | Формирование устойчивой мотивации к обучению решения задач на основе алгоритма решения задач. |
| 5 | Усвоение новых знаний. 1.Анализ текста задачи: задача – объект мышления.
|
- Для решения задачи необходимо составить таблицу. Вопрос учащимся: как назовём колонки таблицы?
-А теперь постараемся её заполнить 1.Какую величину примем за х?
2.Если первая бригада закончила работу на 3 часа раньше, то вторая бригада выполнила работу на 3 часа позже, т.е. вторая бригада выполняла работу на 3 часа больше. 3.Какое кол – во книжных полок должна была изготовить каждая бригада? 4.Сколько книжных полок изготовляла первая бригада в час? 5.Сколько книжных полок изготовляла вторая бригада в час? |
- Работают две бригады; количество книжных полок; время работы каждой бригады; выполнение задания каждой бригадой.
При необходимости пользуются помощью учителя. Создают таблицу.
-1.Время работы первой бригады – х часов 2.Время работы второй бригады – (х + 3) часа
3.По 180 книжных полок.
4.  . .
5. 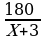 . . | 5 | Формировать умение выделять закономерность, существенную информацию из текста задачи. | Формировать постановку учебной задачи на основе соотнесения того, что уже известно учащимся, и того, что ещё неизвестно. | Уметь с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации. | Формирование познавательно-го интереса. |
| 2.Поиск способа решения задачи и составление плана. | 1.Является ли неизвестное, относительно которого составляется уравнение, искомой величиной? 2.Как найти время работы второй бригады?
3.У какой бригады время, затраченное на работу, меньше? 4.Значит, у какой бригады производительность была больше? 5.На сколько полок больше изготовляла первая бригада, чем вторая? 6.Можем ли мы теперь составить уравнение?
Математическая модель составлена.
| 1.Х – это одна из искомых величин – время работы первой бригады.
2.Найденное значение Х подставить в выражение (Х + 3) и найти время работы второй бригады.
3. У первой бригады.
4.У первой бригады.
5.На 2 полки.
6.Да(учащийся выходит к доске, записывает уравнение).
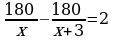
| 4 | Ориентировать в разнообразии способов решения задач. | Определять последователь-ность промежуточных действий с учётом конечного результата, составлять план. | Слушать других, пытаться принимать другую точку зрения, быть готовым изменить свою, развивать умение обмениваться знаниями между одноклассниками для принятия эффективных совместных решений. | Формирование навыков анализа, индивидуаль-ного и коллективного проектирова-ния. |
|
| 3.Работа с составлен-ной математиче-ской моделью | Учитель построчно выводит на экран решение уравнения: 
 
-2х2-6х+540=0 Разделим обе части уравнения на (-2): х2 + 3х – 270 = 0 D = 9 +1080=1089= =332 х1,2 =  х1 = 15; х2 = -18 х(х+3) 0 0 Значит, 15 и -18 – корни составленного рационального уравнения. | Учащиеся комментируют по желанию решение уравнения; записывают его в тетради. | 5 | Ориентироваться на разнообразие способов решения задач. | Корректировать деятельность: вносить изменения в процесс с учётом возникших трудностей и ошибок, намечать способы их устранения.
| Учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его. | Формирование навыков сотрудничества со взрослыми и сверстниками.
|
|
| 4.ответ на вопрос | 1.Что спрашивается в задаче?
2.Какие корни уравнения мы получили? 3.Подходят ли полученные результаты к условию нашей задачи?
4.Что выражается значением Х1 = 15? 5.Решили задачу? 6.Что ещё должны найти? 7.Как? 8.Запишите ответ.
9.Какова главная идея решения данной задачи?
Учитель обращает внимание детей на то, что сравнивать надо величины одного и того же наименования – в данном уравнении – производительность | 1.За сколько часов каждая бригада выполняет задание. 2.Х1 = 15 Х2 = - 18
3. Х2 = - 18 не подходит, т.к. время выполнения задания не может быть отрицательным числом. 4.15 часов работала первая бригада 5. Нет 6.Время работы второй бригады. 7. 15 + 3 = 18 8. Записывают ответ. 9.Дети с помощью учителя: -Зная работу двух бригад(180 кн.п.) и время выполнения данной работы каждой бригады(х и х+3), мы нашли производительность бригад: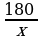 п/ч – I бригада, п/ч – I бригада, 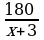 п/ч II бригада. Далее, согласно условию,I б. изготовляла на 2 полки в час больше, чем II б. Значит производительность Iб. ( п/ч II бригада. Далее, согласно условию,I б. изготовляла на 2 полки в час больше, чем II б. Значит производительность Iб. (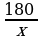 ) больше производительности II б.( ) больше производительности II б.(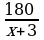 ) на 2 полки в час. На математическом языке это обозначает, ) на 2 полки в час. На математическом языке это обозначает, 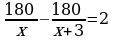 (из большей величины вычитаем меньшую и получили указанную в условии разность). (из большей величины вычитаем меньшую и получили указанную в условии разность).
| 4 | Уметь выделять существенную информацию из текста задачи. | Оценивать весомость приводимых доказательств и рассуждений. | Слушать других, пытаться принимать другую точку зрения, быть готовым изменить свою. | Формирование навыков индивидуаль-ной и коллективной исследователь-ской деятельности. |
| 6 | Этап закрепления новых знаний. | Учитель предлагает поработать детям устно: дана решённая задача. Необходимо найти в ошибку в решении задачи, если она есть, дав полное объяснение решению задачи. Предлагает выполнить задачу 2 и № 5(р.т.)-по парам самостоятельно. № 2: Один кран наполняет бассейн на 6 ч быстрее другого. Два крана, работая вместе, наполняют бассейн за 4 ч. За сколько часов может наполнить водой бассейн каждый кран, работая отдельно? _Решим задачу-привет от учениц 7 класса. | Изучают полученное решение задачи; комментируют, какая величина взята за неизвестное и обозначена за переменную Х; правильно составлена математическая модель задачи; правильно ли выполнена работа с составленной моделью задачи; правильно ли дан ответ на поставленный вопрос задачи. Если в решении задачи есть ошибки – исправляют и обсуждают их вместе с учителем. | 12 | Уметь осуществлять анализ объектов с выделением существенных и несущественных признаков. | Формировать способность к мобилизации сил и энергии, к волевому усилию а преодолении препятствий. | Развивать умение обмениваться знаниями между одноклассниками для принятия эффективных совместных решений. | Формирование интереса к творческой деятельности на основе составленного образца. |
| 7 | Информирование учащихся о домашнем задании. | Подводит итог урока: как работал класс, кто из учащихся работал особенно старательно, что нового узнали учащиеся. Мотивирует д/з: т.к. задания тренировочные, то предлагается учащимся усовершенствовать свои навыки, стремиться к признанию и оценке своего труда. Предлагает дифференцирован-ное д/з.§24,№809,820,823-решить 2 задачи на выбор. Уточняет, все ли поняли д/з? |
Записывают домашнее задание в дневник.
Дают ответ на вопрос. | 2 | Уметь устанавливать причинно – следственные связи. | Составлять план выполнения д/з. | Управлять своим поведением (контроль, самокоррекция, оценка своего действия). | Формировать самодисципли-ну, чувство долга, ответствен-ность. Уметь концентриро-ваться. |
| 8 | Рефлексия деятельности | Оцените свою деятельность на уроке. Выберите соответствующее предложение

| Обводят на выданных листиках номера. | 1 |
|
|
|
|
Приложение 1
| 
| «Если хотите научиться плавать, смело входите в воду, а если хотите научиться решать задачи, то решайте их». Джордж Пойа
|
| «Мне приходится делить время между политикой и уравнением. Однако уравнение, по – моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно». Альберт Эйнштейн |
| 
|
| 
| «Только с алгеброй начинается строгое математическое учение». Николай Иванович Лобачевский
|
| «Величие человека - в его способности мыслить». Блез Паскаль
| 
|
| 
| «Именно математика дает надежнейшие правила: кто им следует – тому не опасен обман чувств». Леонард Эйлер |
| «Где отсутствует точное знание, там действуют догадки, а из десяти догадок девять – ошибки». Максим Горький | 
|
Приложение 2.
Важно запомнить
Рациональные уравнения могут выступать в качестве математических моделей при решении текстовых задач.
Решая такие задачи, надо учитывать особенности каждого этапа их решения.
Первый этап – составление математической модели. Математической моделью может быть как целое, так и дробное рациональное уравнение.
Второй этап – работа с составленной моделью. Решаем рациональное уравнение.
Третий этап – ответ на вопрос задачи. Проверяем, подходят ли найденные корни рационального уравнения условию задачи.
Приложение 3. Лист самооценки и фиксирования результатов деятельности
Фамилия, имя____________________________ класс 8
Тема урока «Решение задач с помощью рациональных уравнений»
| Задания | Оценка |
-

Оценка: все верно – «5», 2 верно - – «4», 1 верно – «3», 0 верных – «2» |
|
-

Оценка: все верно – «5», верно 4 задания – «4», верно 3, 2 задания – «3», верно менее 2 – «2»
|
|
-
Алгоритм решения дробного рационального уравнения: 1) ………………………………………………………………………. 2) ………………………………………………………………………. 3) ………………………………………………………………………. 4) ………………………………………………………………………. 5) ………………………………………………………………………. Оценка: Знаете –«5», не знаете – «2» |
|
-
Решение задачи 1.
Две бригады должны были изготовить по 180 книжных полок. Первая бригада в час изготовляла на 2 полки больше, чем вторая, и потому закончила работу на 3 часа раньше. За сколько часов каждая бригада выполнила задание? х -
Составим и решим уравнение :
Ответ: . |
|
| VI. Решение задач самостоятельно № 5 (р.т.) и № 2 на листе.(РАБОТА В ПАРАХ)
|
|
| VII. Решение задачи № 1091(ПРИВЕТ от 7 КЛАССА) Х-
|
|
| VIII. Тест. 1. Решите уравнение. Выберите верный вариант ответа:  1) 0; 2) 0; 3; 3) 3; -3. 1) 0; 2) 0; 3; 3) 3; -3.
2. Решите уравнение: 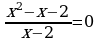 1) 2; -1; 2) -2; 1; 3) -1. 1) 2; -1; 2) -2; 1; 3) -1.
3. Решите уравнение:  1) 2; -3; 2) 1; -2; 3) 1; 1,2. 1) 2; -3; 2) 1; -2; 3) 1; 1,2.
4. Решите уравнение: 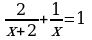 1) -2; 2; 2) 2; 1; 3) 2; -1. 1) -2; 2; 2) 2; 1; 3) 2; -1.
5. Решите уравнение: 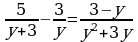 Ответ: __________________ Ответ: __________________
Оценка: верно 5 заданий – «5», верно 4 задания – «4», верно 3, 2 задания – «3», менее 2 – «2» |
|
| IX. Рефлексия:_______________________________________________________________ _______________________________________________________________
|
|
Результат:_________________
ЗАДАЧА 2.
Один кран наполняет бассейн на 6 ч быстрее другого. Два крана, работая вместе, наполняют бассейн за 4 ч. За сколько часов может наполнить водой бассейн каждый кран, работая отдельно?

Верно ли заполнена таблица и составлено уравнение?
. Рабочий должен сделать 286 деталей. Если он будет делать на 8 деталей в день больше, то закончит работу на 1 день раньше срока. Сколько деталей в день рабочий должен делать по плану?
Решение.
|
| Работа (детали) | Производительность (деталей/ день) | Время (дни) |
| По плану | 286 | х | 286/х |
| На самом деле | 286 | х + 10 | 286/(х+10) |
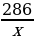 -
-  = 1
= 1
Ответ: 44 детали.
Учитель показывает правило решения и оформление решения следующей задачи на доске.
№1. Две бригады должны были изготовить по 180 книжных полок. Первая бригада в час изготовляла на 2 полки больше, чем вторая, и потому закончила работу на 3 часа раньше. За сколько часов каждая бригада выполнила задание?
| | работа | время | производительность |
| 1 бригада | 180 | 
| 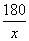
|
| 2 бригада | 180 | 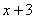
| 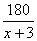
|
Так как производительность первой бригады на 2 полки в час выше, то составим уравнение:
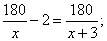

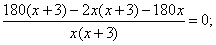
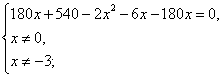
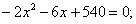
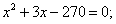
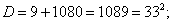
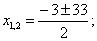

Значение – 18 не подходит по условию задачи (время всегда положительно), значит время работы первой бригады равно 15 часов, а второй 18 часов.
Ответ: Первая бригада работала 15 часов, а вторая – 18 часов.
Дополнительная задача.
Периметр прямоугольного треугольника равен 48 см, один его катет на 4 см больше другого. Чему равны стороны этого треугольника? Составьте математическую модель задачи.
Решение.
Пусть х см — меньший катет треугольника, тогда больший катет равен (х + 4) см. Так как периметр треугольника равен 48 см, то гипотенуза равна 48 - х - (х + 4), т. е. (44 - 2х) см.
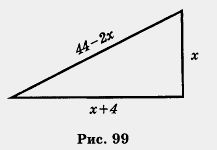
На рис. 99 представлена геометрическая модель задачи: прямоугольный треугольник с обозначенными длинами сторон. Применив к этому треугольнику теорему Пифагора, получим х2 + (х + 4)2 = (44 - 2х)2. Математическая модель задачи составлена.
Замечание. Математическую модель только что решенной задачи можно было составить и по-другому. Пусть, как и раньше, х см — меньший катет, (x + 4) см — больший катет треугольника. Гипотенузу выразим по теореме Пифагора:
 см.
см.
Задача-привет от 7 класса.
Из Курска в Москву, расстояние между которыми 536 км, выехал автомобиль. Через 2,5 ч после начала движения первого автомобиля навстречу ему из Москвы выехал второй автомобиль, который встретился с первым через 2ч после своего выезда.
Найдите скорость каждого автомобиля, если первый проезжает за 1 ч на 5 км больше, чем второй.
-Заполните таблицу и составьте уравнение к задаче.







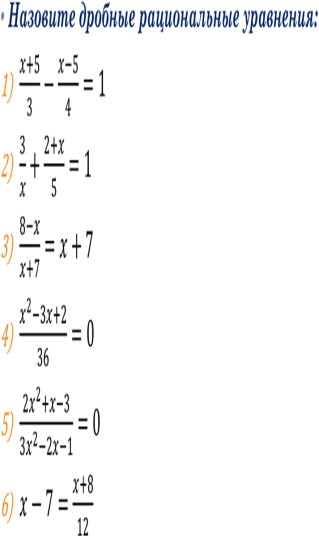
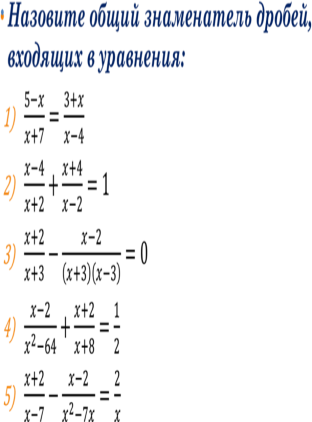
 .
.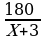 .
.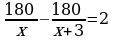




 0
0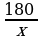 п/ч – I бригада,
п/ч – I бригада, 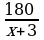 п/ч II бригада. Далее, согласно условию,I б. изготовляла на 2 полки в час больше, чем II б. Значит производительность Iб. (
п/ч II бригада. Далее, согласно условию,I б. изготовляла на 2 полки в час больше, чем II б. Значит производительность Iб. (








 1) 0; 2) 0; 3; 3) 3; -3.
1) 0; 2) 0; 3; 3) 3; -3.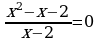 1) 2; -1; 2) -2; 1; 3) -1.
1) 2; -1; 2) -2; 1; 3) -1. 1) 2; -3; 2) 1; -2; 3) 1; 1,2.
1) 2; -3; 2) 1; -2; 3) 1; 1,2.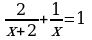 1) -2; 2; 2) 2; 1; 3) 2; -1.
1) -2; 2; 2) 2; 1; 3) 2; -1.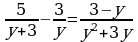 Ответ: __________________
Ответ: __________________
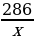 -
-  = 1
= 1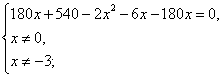

 см.
см. 

















