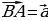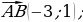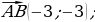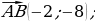| Организационная структура урока |
| Этап урока | Содержание деятельности учителя | Содержание деятельности обучающегося
(осуществляемые действия) | Формируемые способы
деятельности |
| I. Организационный момент | Приветствует обучающихся; проверяет их готовность к уроку. Создает в классе атмосферу психологического комфорта. – Обратите внимание на свои рабочие места. Что вас может отвлекать?
| Настраиваются на учебную деятельность. Концентрируют внимание на работе во время урока. Отвечают на вопросы: – Где я? – Зачем я здесь? – Что мне нужно делать? | Формируют навыки самоорганизации |
| II. Актуализация опорных знаний и жизненного опыта. Постановка учебной задачи | Предлагает учащимся определить, какие понятия они знают и понимают и какие им еще недостаточно известны.
Вопрос запуска постановки учебной задачи: – Достаточно ли у вас знаний о нахождении координат вектора? Формулирует учебную задачу: – Исследовать координаты вектора | Заполняют таблицу. | Понятия | Знаю(+) / Не знаю (–) | | Вектор | + | | Нулевой вектор | + | | Модуль вектора | + | | Коллинеарные векторы | + | | Координаты вектора | – | | Сравнение векторов | – | Осознают важность решения поставленной учебной задачи. | Развивают навыки целеполагания |
| III. Сообщение темы. Постановка цели и задач урока | Сообщает тему урока. Организует совместное с учащимися формулирование цели и задач урока. – Внимательно прочитайте тему урока. – Что от вас ожидается на уроке? – Какие цели и задачи вы можете перед собой поставить? | Записывают в тетрадь тему урока. Участвуют в формулировании целей и задач урока: – усвоить суть понятия «координаты вектора»; – научиться определять координаты вектора, заданного координатами его начала и конца; – научиться сравнивать вектора | Формируют умения принимать и сохранять учебную задачу |
| IV. Мотивирование к учебной деятельности | Способствует обсуждению мотивационных вопросов: – Почему для меня важно разобраться с координатами вектора? – Где я смогу использовать знания о координатах вектора? – Насколько мне интересно узнавать о координатах вектора? – Какова моя цель на данный урок? | Отвечают на мотивационные вопросы. Создают условия для успешной учебной деятельности. | Формируют умения выражать свои мысли. Развивают навыки самомотивации |
| V. Создание ситуации затруднения. Работа над темой урока | Организует обсуждение проблемного вопроса: – Как найти координаты вектора?
Организует анализ информации. Демонстрирует и поясняет иллюстрацию: 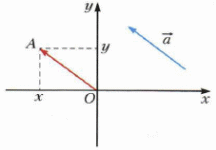
Отвечает на вопросы учащихся. Стимулирует самостоятельный поиск ответов на вопросы. Способствует организации дополнительных исследований и поиску информации.
Обращает внимание учащихся на иллюстрацию и просит определить координаты векторов 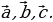
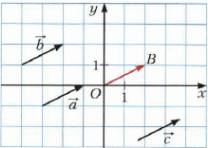
Организует анализ теоремы. Способствует изучению доказательства теоремы. Отвечает на вопросы учащихся
| Принимают участие в обсуждении проблемного вопроса. Испытывают определенные трудности при ответе на вопрос. Выбирают, как им лучше всего будет организовать свою работу на уроке по изучению нового материала: А) буду самостоятельно изучать новый материал; Б) буду работать в паре; В) буду работать в группе. Анализируют информацию. Формулируют вопросы учителю. Проводят дополнительные исследования. | Информация | Мне непонятно… Вопросы учителю | | Рассмотрим на координатной плоскости вектор 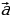 | Как…? | | От начала координат отложим равный ему вектор 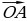 | Почему…? | | Координатами вектора 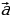 называют координаты точки А называют координаты точки А | Что…? | | Запись 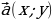 означает, что вектор означает, что вектор 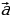 имеет координаты имеет координаты 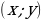 | Каким образом…? | | Числа 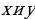 называют соответственно первой и второй координатами вектора называют соответственно первой и второй координатами вектора 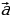 | Где…? |
Обсуждают в группах или в парах решения поставленной задачи. Проводят дополнительные исследования. Выясняют, что равные векторы имеют равные соответствующие координаты. Каждый из равных векторов 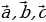 имеют координаты (2; 1). имеют координаты (2; 1). Узнают, что справедливо обратное утверждение: если соответствующие координаты векторов равны, то равны и сами векторы.
Анализируют теорему. Изучают доказательство теоремы. Заполняют таблицу. | Теорема | Комментарий ученика к доказательству теоремы | | Если точки 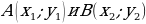 соответственно являются началом и концом вектора соответственно являются началом и концом вектора 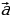 , то числа , то числа 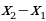 и и 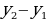 равны соответственно первой и второй координатам вектора равны соответственно первой и второй координатам вектора 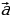 |
|
| Выражают свои мысли в соответствии с задачей.
Анализируют информацию
|
| VI. Закрепление изученного материала | Организует самоанализ усвоенных учащимися знаний. Оказывает помощь ученикам, которые не знают ответов на вопросы. Создает условия для дополнительного изучения вопросов, которые вызвали затруднения
| Отвечают на вопросы. Определяют свой уровень усвоения знаний. Заполняют таблицу. | Вопросы | Варианты ответов | | Знаю ответ на вопрос (+) | Не знаю ответ на вопрос (+) | | Что можно сказать о координатах равных векторов? |
|
| | Что можно сказать о векторах, соответствующие координаты которых равны? |
|
| | Как найти координаты вектора, если известны координаты его начала и конца? |
|
| | Как найти модуль вектора, если известны его координаты? |
|
| Анализируют ответы на вопросы. Проводят дополнительное изучение нового материала. Задают вопросы учителю |
|
| VII. Решение заданий | Задания. 1. (№ 406) Найдите координаты вектора 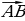 , если: , если: 1) А (2; 3), В (–1; 4); 2) А (3; 0), В (0; –3); 3) А (0; 0), В (–2; –8); 4) 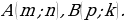 2. (№ 447) Даны точка А (1; 3) и вектор 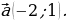 Найдите координаты точки В такой, что векторы Найдите координаты точки В такой, что векторы 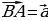 | Решение. 1. 1) 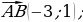 2) 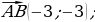 3) 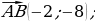 4) 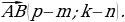 2. В(х; у) – ? 1 – х = –2 х = 3; 3 – у = 1 у = 2 В(3; 2) | Развивают умения самостоятельно принимать решения |
| VIII. Подведение итогов урока. Рефлексия | Организует подведение итогов урока обучающимися. Способствует размышлению учащихся над вопросами: – Что нового я узнал на уроке? – Понравилось ли мне изучать тему «Координаты вектора»? – Получаю ли я удовольствие от умственной работы на уроках геометрии? – Могу ли я лучше учиться? | Подводят итоги своей работы на уроке. Проводят самооценку, рефлексию. | Отслеживают цель учебной деятельности |
| IX. Домашнее задание | Помогает учащимся выбрать задания из учебника. Обращает внимание на возможности и способности учащихся | Выбирают задания, которые будут решать дома. Записывают домашнее задание. | Формируют навыки самоорганизации |








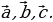

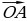
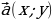 означает, что вектор
означает, что вектор 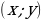
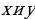 называют соответственно первой и второй координатами вектора
называют соответственно первой и второй координатами вектора 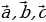 имеют координаты (2; 1).
имеют координаты (2; 1).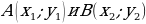 соответственно являются началом и концом вектора
соответственно являются началом и концом вектора 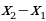 и
и 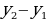 равны соответственно первой и второй координатам вектора
равны соответственно первой и второй координатам вектора 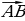 , если:
, если: 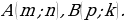
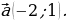 Найдите координаты точки В такой, что векторы
Найдите координаты точки В такой, что векторы