| Организует изучение учебного материала по учебнику Объяснение материала проводится в несколько этапов. 1. Введение основных понятий. Начать следует с известных учащимся понятий. Так, они знают, что выражение 5x2 + 3x – 2 является многочленом второй степени с одной переменной. Сообщить им, что такой многочлен имеет специальное название – «квадратный трехчлен». Понятие 1. Квадратный трехчлен. Определение. Квадратным трехчленом называется многочлен вида ax2 + bx + c, где х – переменная, а, b и с – некоторые числа, причем а ≠ 0. Для усвоения понятия следует дать учащимся задание: определить, какие из следующих выражений являются квадратным трехчленом; ответ объяснить. а) 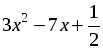 ; г) 2x – 1;27 ; г) 2x – 1;27 б) 2x3 + 5x – 1; д) 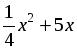 ; ; в) 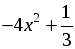 ; е) ; е) 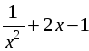 . . Далее заметить, что значение квадратного трехчлена 5x2 + 3x – 2 зависит от значения х. Например, если х = 0, то 5x2 + 3x – 2 = –2; если х = 2, то 5x2 + 3x – 2 = 24; если х = –1, то 5x2 + 3x – 2 = 0. Обратить внимание учащихся, что при х = –1 квадратный трехчлен 5x2 + 3x – 2 обращается в нуль. Сообщить им, что в этом случае число –1 называют корнем данного квадратного трехчлена и попросить их сформулировать определение корня квадратного трехчлена. Понятие 2. Корень квадратного трехчлена. Определение. Корнем квадратного трехчлена называется значение переменной, при котором значение этого трехчлена равно нулю. Спросить учащихся, как отыскать корни квадратного трехчлена (решить соответствующее квадратное уравнение). Предложить им найти корни квадратного трехчлена 5x2 + 3x – 2. Затем заметить, что количество корней квадратного трехчлена зависит от количества корней соответствующего квадратного уравнения, которое, в свою очередь, зависит от дискриминанта. Так появляется новое понятие – дискриминант квадратного трехчлена. Понятие 3. Дискриминант квадратного трехчлена. Определение. Дискриминантом квадратного трехчлена ax2 + bx + c называется значение выражения D = b2 – 4ac. Сделать вывод, что если D 0, то квадратный трехчлен имеет два корня; если D = 0, то один корень; если D 2. Формула для разложения на множители квадратного трехчлена. Обратить внимание учащихся, что существует ряд задач, в которых требуется разложить на множители квадратный трехчлен. Затем показать им, как это можно сделать с помощью группировки (с. 128 учебника). После доказательства формулы разложения на множители квадратного трехчлена вынести на доску запись: | Если x1 и x2 – корни квадратного трехчлена ax2 + bx + c,
то ax2 + bx + c = a(x – x1)(x – x2). | Сделать вывод: если квадратный трехчлен имеет корни, то он раскладывается на множители. Затем задать учащимся вопрос: можно ли разложить на множители квадратный трехчлен, не имеющий корней? В классе с высоким уровнем подготовки можно привести доказательство соответствующего утверждения. Доказательство. Пусть трехчлен ax2 + bx + c не имеет корней. Предположим, что его можно представить в виде произведения многочленов первой степени: ax2 + bx + c = (kx + m)(px + q), где k, m, p и q – некоторые числа, причем k ≠ 0 и p ≠ 0. Произведение (kx + m)(px + q) обращается в нуль при 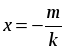 и и 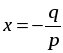 . Следовательно, при этих значениях х обращается в нуль и трехчлен ax2 + bx + c, то есть числа . Следовательно, при этих значениях х обращается в нуль и трехчлен ax2 + bx + c, то есть числа 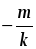 и и 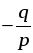 являются его корнями. Мы пришли к противоречию, так как по условию этот трехчлен корней не имеет. являются его корнями. Мы пришли к противоречию, так как по условию этот трехчлен корней не имеет. Итогом этого этапа объяснения материала должны быть следующие усвоенные учащимися утверждения: – если квадратный трехчлен имеет корни, то его можно разложить на множители; если квадратный трехчлен корней не имеет, то на множители (линейные) разложить его нельзя; – чтобы выяснить, разлагается ли трехчлен на множители, достаточно вычислить его дискриминант; – существует специальная формула, с помощью которой квадратный трехчлен, имеющий корни, можно разложить на множители: ax2 + bx + c =
= a(x – x1)(x – x2). 3. Примеры разложения на множители квадратных трехчленов. Разобрать предложенные в учебнике примеры разложения квадратных трехчленов на множители, предложив при этом образец оформления соответствующих рассуждений. Пример. Разложить на множители трехчлен –3x2 – 5x + 2. Сначала следует сделать следующую запись: –3x2 – 5x + 2 = –3(х – ) (х – ). Затем найти корни данного квадратного трехчлена: –3x2 – 5x + 2 = 0; 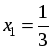 и x2 = –2. и x2 = –2. Эти корни записать в оставленное для них место, а затем можно выполнить некоторые преобразования. | 






 .
.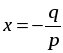 . Следовательно, при этих значениях х обращается в нуль и трехчлен ax2 + bx + c, то есть числа
. Следовательно, при этих значениях х обращается в нуль и трехчлен ax2 + bx + c, то есть числа 
















