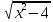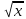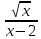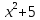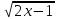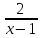Тема: Понятие функции. Область определения и множество значений функции.

План урока.

Преподаватель: Жаурова Л.А.

Тема: Понятие функции. Область определения и множество значений функции.

Цели:

Предметные:

• Студенты должны знать понятия функции, графики функции, область определения и множество значений функции.

• Развивать умения построения графиков функций.

Метапредметные:

• уметь самостоятельно добывать новые для себя математические знания, используя для этого доступные источники информации;

• уметь выстраивать конструктивные взаимодействия в команде по решению общих задач;

• уметь управлять своей познавательной деятельностью, проводить самооценку уровня собственного интеллектуального развития.

Личностные:

• осуществлять поиск полученной информации для нахождения области определения и множества значений функций.

Методы обучения:

• по источнику получения информации: словесный, практический;

• по характеру познавательной деятельности: беседа, репродуктивный, проблемные вопросы;

• активные методы обучения: обсуждение, самостоятельная работа, метод частично – поисковый.

Тип урока:

• Обобщение и систематизация знаний.

Элементы педагогических технологий:

• погружения;

• информационно-коммуникационная технология;

• дифференцированное обучение.

Межпредметные связи:

• Физика;

• Химия;

• Техническая механика.

План урока.

1. Организационная момент (приветствие, проверка присутствующих и готовность студентов к уроку).

2. «Погружение»

3. Повторение опорных знаний.

4. Изложение нового материала.

5. Закрепление.

6. Домашние задание.

Ход урока.

1. Организационная момент (приветствие, проверка присутствующих и готовность студентов к уроку).

2. «Погружение»

Идея зависимости величин восходит к древнегреческой науке. Развитие механики и техники 16 – 17 вв. потребовало введение общего понятия функции, что было сделано немецким философом и математиком Г. Лейбницем (1646 – 1716 гг). П. Ферма

и Р. Декарт показали, как представить функции аналитически. Декарт ввел в математику понятие переменной величины.

Строгое определение функции дал И. Бернулли (1667 – 1748 гг.), а затем его ученик, член Петербургской Академии Л. Эйлер ввел обозначение f (x) и объявил понятие функции центральным понятием анализа.

Позднее Ж. Фурье, Н. И. Лобачевский, И. П. Декарт и другие внесли большой вклад в развитие понятия функции. Установление функциональной зависимости между величинами иллюстрирует важные философские категории – причины и следствия.

3. Повторение опорных знаний.

3.1 Вопросы:

• Какие функции вы знаете?

• Каким уравнением задаётся линейная функция?

• Каким уравнением задаётся квадратичная функция?

3.2 Построить графики функций:

y = 2x,

,

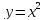y=,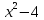

y=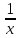

4. Изложение нового материала.

Понятие функций

Определение:

Если каждому допустимому значению X соответствует определенное значение Y называется функцией.

y = f (x) – символическая запись функции;

X – независимая переменная (аргумент);

Y – зависимая переменная от X ;

X – область определения или значение X, при которых функция имеет смысл;

Y – множество значений;

D ( f ) – область определения

E ( f ) – область значений

5. Закрепление.

5.1 Построить графики функций и найти их область определения и область значения:

y = 2x
y =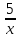

y =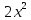

y =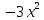

y =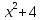

5.2 Вычислить:

1) y (3) =?, y (-2) =?, если f (x) = ;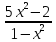

2) y (-1) =?, если y = ;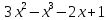

5.3 Найти область определения функции:

y =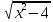

5.4 Найти область определения функций (самостоятельно):

y =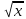

y =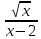

y =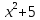

y =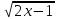

y =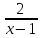

6. Домашнее задание.

7. Список используемой литературы

Богомолов Н.В. Математика: учеб. для ссузов.
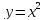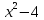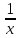
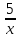
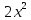
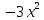
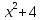
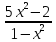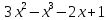