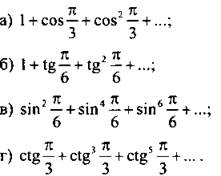План урока
Предмет: математика
Преподаватель: Амирханова А. К.
Дата проведении:__________
Тема урока: Числовая окружность (обобщающее занятие)
Цель: рассмотреть понятия, связанные с числовой окружностью.
Ход урока
I. Сообщение темы и цели урока
II. Изучение нового материала
Обычно углы в геометрии рассматриваются при пересечении прямых в многоугольниках (в частности, в треугольниках). При этом рассматриваемые углы составляют менее 360°. В физике (для колебательных, волновых и других процессов) приходится учитывать углы и больше 360°. Поэтому возникает понятие обобщенного угла.

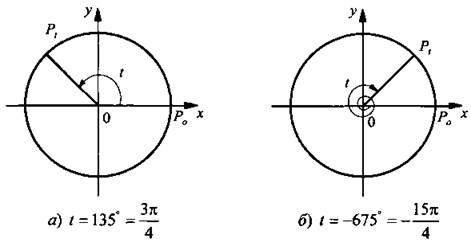
Рассмотрим окружность радиуса 1 с центром в начале координат, которую называют числовой окружностью. Возьмем точку Р0 (1; 0). Сместим эту точку по окружности и получим точку Рt. При этом смещение может происходить и по часовой стрелке, и против часовой стрелки на любую величину (как меньше одного оборота, как и больше одного оборота). Будем считать ∠P0OPt обобщенным углом {или просто углом) t. Углы, полученные поворотом точки Р0 против часовой стрелки, считаются положительными, по часовой стрелке - отрицательными. Принято указывать направление поворота стрелкой, а в случае более одного оборота - число оборотов. Например, на рисунке показаны положительный (а) и отрицательный (б) углы.

В тригонометрии величины углов, как правило, измеряются в радианах и значительно реже - в градусах. При этом за угол, равный 1 радиану (1 рад; слово «рад» обычно не пишут), принимают центральный угол, опирающийся на дугу окружности длиной, равной радиусу окружности; за угол, равный 1 градусу (1°), - центральный угол, опирающийся на дугу окружности длиной, равной 1/360 длины окружности. Рассматривая единичную окружность, получаем, что ее длина равна 2π. Поэтому между радианной и градусной мерой существует простое соотношение: 2п = 360° или п = 180°. Тогда 
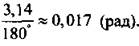
Пример 1
Запишем в других единицах измерения углы:

Учтем, что 1 (рад) = (180/π). Тогда получим:

Учтем, что 1° = π/180 (рад). Тогда имеем:

В частности, на последнем рисунке приведены углы:

Заметим, что использование радианной меры углов обусловлено, в том числе, более простой записью ряда формул. Для окружности радиуса R длина l ее дуги в t радиан вычисляется по формуле l = tR. Если дуга содержит n°, то аналогичная формула имеет вид:  Также площадь S сектора крута радиуса R, дуга которого содержит t радиан вычисляется по формуле
Также площадь S сектора крута радиуса R, дуга которого содержит t радиан вычисляется по формуле  Если дуга содержит n°, то аналогичная формула имеет вид:
Если дуга содержит n°, то аналогичная формула имеет вид: 
Теперь напомним определения основных тригонометрических функций, введенные в курсе геометрии.
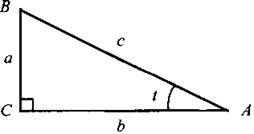
Рассмотрим прямоугольный треугольник ABC с катетами а и b и гипотенузой с, с острым углом t. Тогда sin t = a/c (отношение противолежащего катета к гипотенузе); cos t = b/c(отношение прилежащего катета к гипотенузе); tg t = a/b (отношение противолежащего катета к прилежащему катету); ctg t = b/a (отношение прилежащего катета к противолежащему катету).
Для данного угла t отношения a/c, b/c, a/b, b/a не зависят от величин а, b и с.

Действительно, рассмотрим два подобных прямоугольных треугольника ABC и АВ1С1 с общим острым углом t, катетами ВС = а, В1С1 = а1 и гипотенузами АВ = с, АВ1 = с1. По определению синуса из этих треугольников имеем:  Но с другой стороны, из подобия треугольников получаем:
Но с другой стороны, из подобия треугольников получаем:  или
или  . Поэтому отношения
. Поэтому отношения  не зависят от величин а, с, а1, c1 и зависят только от величины угла t. Следовательно, sin t (как и остальные значения cos t, tg t, ctg t) являются функциями угла t.
не зависят от величин а, с, а1, c1 и зависят только от величины угла t. Следовательно, sin t (как и остальные значения cos t, tg t, ctg t) являются функциями угла t.
Пример 2
Найдем значения тригонометрических функций для π/6.
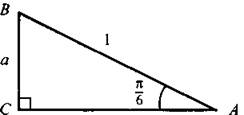
Так как тригонометрические функции угла не зависят от сторон треугольника, то рассмотрим прямоугольный треугольник с гипотенузой АВ = 1 и острым углом А = π/6 = 30°. В таком треугольнике  Тогда по теореме Пифагора
Тогда по теореме Пифагора 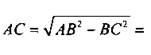
 Теперь легко найти все тригонометрические функции:
Теперь легко найти все тригонометрические функции: 

Для любого угла приближенные значения основных тригонометрических функций находятся с помощью калькулятора или таблиц. Для некоторых углов можно найти и точные значения тригонометрических функций, аналогично примеру 2. Эти значения приведены в таблице. Знак «-» в таблице означает, что данная функция при этом значении аргумента не определена (не существует).
|
Аргумент t
|
Функция
|
|
sin t
|
cos t
|
tg t
|
ctg t
|
|
0° = 0
|
0
|
1
|
0
|
-
|
|
30° = π/6
|
1/2
|

|
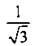
|

|
|
45° = π/4
|

|

|
1
|
1
|
|
60° = π/3
|

|
1/2
|
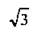
|
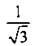
|
|
90° = π/2
|
1
|
0
|
-
|
0
|
Заметим, что достаточно помнить значения только первых трех строк этой таблицы. Используя свойства тригонометрических функций и формулы приведения (см. следующие уроки), можно находить значения тригонометрических функций и для других углов, связанных с углами 0, π/6, π/4.
Пример 3
Вычислим, используя данные приведенной таблицы:

 (учтено, что слагаемые образуют бесконечно убывающую геометрическую прогрессию).
(учтено, что слагаемые образуют бесконечно убывающую геометрическую прогрессию).
Пример 4
Известно, что 
Найдем 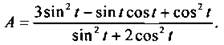
Найдем связь между sin t и cos t, используя условие задачи 
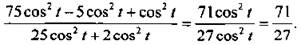
Заметим, что полученный ответ справедлив при cos t ≠ 0. Однако cos t не может равняться нулю, так как это противоречит условию задачи. Действительно, если cos t = 0, то выражение 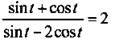 имеет вид:
имеет вид: 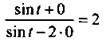 или l = 2. Так как это неравенство неверное, то cos t ≠ 0.
или l = 2. Так как это неравенство неверное, то cos t ≠ 0.
III. Контрольные вопросы
1. Как строится угол на числовой окружности?
2. Дайте определение 1 радиана и 1 градуса.
3. Какая связь между радианной и градусной мерами угла?
4. Дайте определение основных тригонометрических функций.
IV. Задание на уроке
§ 4, № 1; 3; 7; 12 (а, б); 13 (в, г); 14; 17; 19;
§ 5, № 1; 4; 6; 8; 10 (а, 6); 11; 13.
V. Задание на дом
§ 4, № 2; 4; 9; 12 (в, г); 13 (а, б); 15; 18; 20;
§ 5, № 2; 5; 7; 9; 10 (в, г); 12; 14.
VI. Творческие задания
1. Вычислите:

Ответы: 
2. Известно, что 
Найдите 
Ответ: 22/27.
3. Известно, что 
Найдите 
Ответ: 20/17.
VII. Подведение итогов урока
Просмотр содержимого документа
«Тема урока: Числовая окружность (обобщающее занятие)»
План урока
Предмет: математика
Преподаватель: Амирханова А. К.
Дата проведении:__________
Тема урока: Числовая окружность (обобщающее занятие)
Цель: рассмотреть понятия, связанные с числовой окружностью.
Ход урока
I. Сообщение темы и цели урока
II. Изучение нового материала
Обычно углы в геометрии рассматриваются при пересечении прямых в многоугольниках (в частности, в треугольниках). При этом рассматриваемые углы составляют менее 360°. В физике (для колебательных, волновых и других процессов) приходится учитывать углы и больше 360°. Поэтому возникает понятие обобщенного угла.
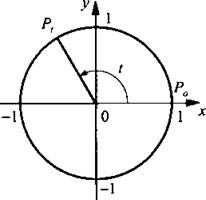
Рассмотрим окружность радиуса 1 с центром в начале координат, которую называют числовой окружностью. Возьмем точку Р0 (1; 0). Сместим эту точку по окружности и получим точку Рt. При этом смещение может происходить и по часовой стрелке, и против часовой стрелки на любую величину (как меньше одного оборота, как и больше одного оборота). Будем считать ∠P0OPt обобщенным углом {или просто углом) t. Углы, полученные поворотом точки Р0 против часовой стрелки, считаются положительными, по часовой стрелке - отрицательными. Принято указывать направление поворота стрелкой, а в случае более одного оборота - число оборотов. Например, на рисунке показаны положительный (а) и отрицательный (б) углы.
В тригонометрии величины углов, как правило, измеряются в радианах и значительно реже - в градусах. При этом за угол, равный 1 радиану (1 рад; слово «рад» обычно не пишут), принимают центральный угол, опирающийся на дугу окружности длиной, равной радиусу окружности; за угол, равный 1 градусу (1°), - центральный угол, опирающийся на дугу окружности длиной, равной 1/360 длины окружности. Рассматривая единичную окружность, получаем, что ее длина равна 2π. Поэтому между радианной и градусной мерой существует простое соотношение: 2п = 360° или п = 180°. Тогда 
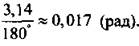
Пример 1
Запишем в других единицах измерения углы:
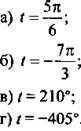
Учтем, что 1 (рад) = (180/π). Тогда получим:

Учтем, что 1° = π/180 (рад). Тогда имеем:
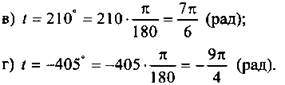
В частности, на последнем рисунке приведены углы:
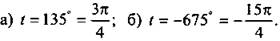
Заметим, что использование радианной меры углов обусловлено, в том числе, более простой записью ряда формул. Для окружности радиуса R длина l ее дуги в t радиан вычисляется по формуле l = tR. Если дуга содержит n°, то аналогичная формула имеет вид: 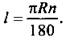 Также площадь S сектора крута радиуса R, дуга которого содержит t радиан вычисляется по формуле
Также площадь S сектора крута радиуса R, дуга которого содержит t радиан вычисляется по формуле 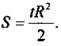 Если дуга содержит n°, то аналогичная формула имеет вид:
Если дуга содержит n°, то аналогичная формула имеет вид: 
Теперь напомним определения основных тригонометрических функций, введенные в курсе геометрии.
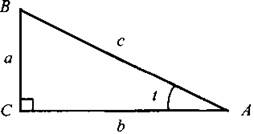
Рассмотрим прямоугольный треугольник ABC с катетами а и b и гипотенузой с, с острым углом t. Тогда sin t = a/c (отношение противолежащего катета к гипотенузе); cos t = b/c(отношение прилежащего катета к гипотенузе); tg t = a/b (отношение противолежащего катета к прилежащему катету); ctg t = b/a (отношение прилежащего катета к противолежащему катету).
Для данного угла t отношения a/c, b/c, a/b, b/a не зависят от величин а, b и с.
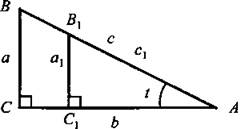
Действительно, рассмотрим два подобных прямоугольных треугольника ABC и АВ1С1 с общим острым углом t, катетами ВС = а, В1С1 = а1 и гипотенузами АВ = с, АВ1 = с1. По определению синуса из этих треугольников имеем:  Но с другой стороны, из подобия треугольников получаем:
Но с другой стороны, из подобия треугольников получаем:  или
или  . Поэтому отношения
. Поэтому отношения 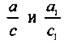 не зависят от величин а, с, а1, c1 и зависят только от величины угла t. Следовательно, sin t (как и остальные значения cos t, tg t, ctg t) являются функциями угла t.
не зависят от величин а, с, а1, c1 и зависят только от величины угла t. Следовательно, sin t (как и остальные значения cos t, tg t, ctg t) являются функциями угла t.
Пример 2
Найдем значения тригонометрических функций для π/6.

Так как тригонометрические функции угла не зависят от сторон треугольника, то рассмотрим прямоугольный треугольник с гипотенузой АВ = 1 и острым углом А = π/6 = 30°. В таком треугольнике  Тогда по теореме Пифагора
Тогда по теореме Пифагора 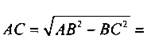
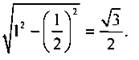 Теперь легко найти все тригонометрические функции:
Теперь легко найти все тригонометрические функции: 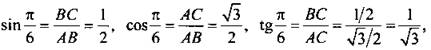
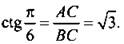
Для любого угла приближенные значения основных тригонометрических функций находятся с помощью калькулятора или таблиц. Для некоторых углов можно найти и точные значения тригонометрических функций, аналогично примеру 2. Эти значения приведены в таблице. Знак «-» в таблице означает, что данная функция при этом значении аргумента не определена (не существует).
| Аргумент t | Функция |
| sin t | cos t | tg t | ctg t |
| 0° = 0 | 0 | 1 | 0 | - |
| 30° = π/6 | 1/2 | 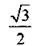
| 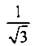
| 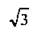
|
| 45° = π/4 | 
| 
| 1 | 1 |
| 60° = π/3 | 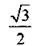
| 1/2 | 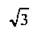
| 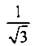
|
| 90° = π/2 | 1 | 0 | - | 0 |
Заметим, что достаточно помнить значения только первых трех строк этой таблицы. Используя свойства тригонометрических функций и формулы приведения (см. следующие уроки), можно находить значения тригонометрических функций и для других углов, связанных с углами 0, π/6, π/4.
Пример 3
Вычислим, используя данные приведенной таблицы:

 (учтено, что слагаемые образуют бесконечно убывающую геометрическую прогрессию).
(учтено, что слагаемые образуют бесконечно убывающую геометрическую прогрессию).
Пример 4
Известно, что 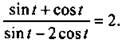
Найдем 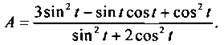
Найдем связь между sin t и cos t, используя условие задачи 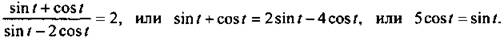 Подставим sin t в выражение А:
Подставим sin t в выражение А: 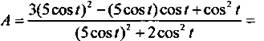
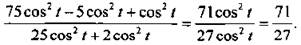
Заметим, что полученный ответ справедлив при cos t ≠ 0. Однако cos t не может равняться нулю, так как это противоречит условию задачи. Действительно, если cos t = 0, то выражение 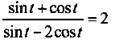 имеет вид:
имеет вид: 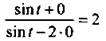 или l = 2. Так как это неравенство неверное, то cos t ≠ 0.
или l = 2. Так как это неравенство неверное, то cos t ≠ 0.
III. Контрольные вопросы
1. Как строится угол на числовой окружности?
2. Дайте определение 1 радиана и 1 градуса.
3. Какая связь между радианной и градусной мерами угла?
4. Дайте определение основных тригонометрических функций.
IV. Задание на уроке
§ 4, № 1; 3; 7; 12 (а, б); 13 (в, г); 14; 17; 19;
§ 5, № 1; 4; 6; 8; 10 (а, 6); 11; 13.
V. Задание на дом
§ 4, № 2; 4; 9; 12 (в, г); 13 (а, б); 15; 18; 20;
§ 5, № 2; 5; 7; 9; 10 (в, г); 12; 14.
VI. Творческие задания
1. Вычислите:
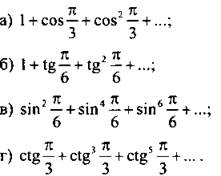
Ответы: 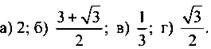
2. Известно, что 
Найдите 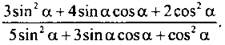
Ответ: 22/27.
3. Известно, что 
Найдите 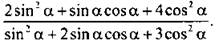
Ответ: 20/17.
VII. Подведение итогов урока









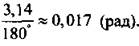




 Также площадь S сектора крута радиуса R, дуга которого содержит t радиан вычисляется по формуле
Также площадь S сектора крута радиуса R, дуга которого содержит t радиан вычисляется по формуле  Если дуга содержит n°, то аналогичная формула имеет вид:
Если дуга содержит n°, то аналогичная формула имеет вид: 


 Но с другой стороны, из подобия треугольников получаем:
Но с другой стороны, из подобия треугольников получаем:  или
или  . Поэтому отношения
. Поэтому отношения  не зависят от величин а, с, а1, c1 и зависят только от величины угла t. Следовательно, sin t (как и остальные значения cos t, tg t, ctg t) являются функциями угла t.
не зависят от величин а, с, а1, c1 и зависят только от величины угла t. Следовательно, sin t (как и остальные значения cos t, tg t, ctg t) являются функциями угла t.
 Тогда по теореме Пифагора
Тогда по теореме Пифагора 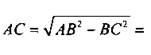
 Теперь легко найти все тригонометрические функции:
Теперь легко найти все тригонометрические функции: 


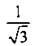


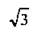

 (учтено, что слагаемые образуют бесконечно убывающую геометрическую прогрессию).
(учтено, что слагаемые образуют бесконечно убывающую геометрическую прогрессию).
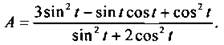

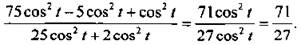
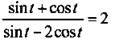 имеет вид:
имеет вид: 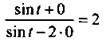 или l = 2. Так как это неравенство неверное, то cos t ≠ 0.
или l = 2. Так как это неравенство неверное, то cos t ≠ 0.







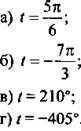

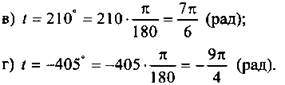



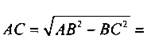
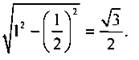 Теперь легко найти все тригонометрические функции:
Теперь легко найти все тригонометрические функции: 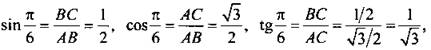

 (учтено, что слагаемые образуют бесконечно убывающую геометрическую прогрессию).
(учтено, что слагаемые образуют бесконечно убывающую геометрическую прогрессию).