План урока
Предмет: математика
Преподаватель: Амирханова А. К.
Дата проведении:__________
Тема урока: Зачетная работа по теме «Числовые функции»
Цель: проверить знания учащихся по вариантам одинаковой сложности.
Ход уроков
I. Сообщение темы и цели уроков
II. Характеристика зачетной работы
Работа составлена в двух равноценных вариантах. По сравнению с контрольной работой увеличено количество заданий. Соответственно, у учащихся появляется возможность выбора задач. Все задания разбиты на три части: А, В и С. Самые простые задачи находятся в части А, более сложные - в части В, еще сложнее - в части С. Каждая задача из части А оценивается в 1 балл, из В - в 2 балла, из С - в 3 балла. Поэтому за правильное решение всех задач части А можно получить 7 баллов, части В - 8 баллов и части С - 9 баллов (всего 24 балла). Оценка «3» ставится за 6 баллов, оценка «4» - за 10 баллов, оценка «5» - за 14 баллов.
Так как эта работа является зачетной, то в нее не включены принципиально новые задачи. Поэтому разбору заданий работы отдельного урока можно и не посвящать (решения задач могут быть вывешены на стенде). Для стендового размещения разбор вариантов приводится.
III. Варианты зачетной работы
Вариант 1
А
1. Найдите область определения функции 
2. Определите область значений функции 
3. Найдите промежутки возрастания и убывания функции  ее наибольшее и наименьшее значения.
ее наибольшее и наименьшее значения.
4. Определите четность или нечетность функции 

5. Найдите значение функции  при х = 0,5-1.
при х = 0,5-1.
6. Постройте график функции:

В
7. Даны функции  Найдите значение выражения
Найдите значение выражения  при х = -0,3.
при х = -0,3.
8. Дана функция /(х) = 4х2 - х. Решите уравнение /(/(х)) = 33.
9. Постройте график функции:

C
10. Найдите область значений функции 
11. Дана функция  где коэффициенты а, b, с, d, k, mмогут принимать значения 0 и 1. Найдите значения а, b, с, d, k, m, для которых f(2) = 42.
где коэффициенты а, b, с, d, k, mмогут принимать значения 0 и 1. Найдите значения а, b, с, d, k, m, для которых f(2) = 42.
12. Постройте график функции 
Вариант 2
1. Найдите область определения функции 
2. Определите область значений функции f(х) = 3х2 - 12х + 1.
3. Найдите промежутки возрастания и убывания функции  ее наибольшее и наименьшее значения.
ее наибольшее и наименьшее значения.
4. Определите четность или нечетность функции 

5. Найдите значение функции  при х = 0,2-1.
при х = 0,2-1.
6. Постройте график функции:

В
7. Даны функции  Найдите значение выражения
Найдите значение выражения  при х = -0,7.
при х = -0,7.
8. Дана функция f(х) = 5х2 - х. Решите уравнение f(f(х)) = 76.
9. Постройте график функции:

C
10. Найдите область значений функции 
11. Дана функция  где коэффициенты а, b, с, d, k, mмогут принимать значения 0 и 1. Найдите значения а, b, с, d, k, m, для которых f(2) = 40.
где коэффициенты а, b, с, d, k, mмогут принимать значения 0 и 1. Найдите значения а, b, с, d, k, m, для которых f(2) = 40.
12. Постройте график функции 
IV. Ответы и решения
Вариант 1

3. Функция возрастает на промежутке [-5; 0] и убывает на промежутке [0; 5], 
4. Функция нечетная.

6. а, б построены.
7. 1,08.

9. а, б построены.
10. Разделим числитель дроби на знаменатель и выделим целую часть. Получим:  Введем новую переменную t = х - 2 и запишем функцию в виде
Введем новую переменную t = х - 2 и запишем функцию в виде  Очевидно, что эта функция нечетная. Рассмотрим промежуток t ∈ (0; +∞) и напишем неравенство для среднего арифметического и среднего геометрического. Получим:
Очевидно, что эта функция нечетная. Рассмотрим промежуток t ∈ (0; +∞) и напишем неравенство для среднего арифметического и среднего геометрического. Получим:  или
или  Неравенство переходит в равенство при t = 25/t, т. е. t = 5 (или х - 2 = 5, т. е. х = 7). При t ∈ (-∞; 0) имеем: f(t) ≤ -10. Неравенство переходит в равенство при t = -5 (или х - 2 = -5, т. е. х = -3). Итак,
Неравенство переходит в равенство при t = 25/t, т. е. t = 5 (или х - 2 = 5, т. е. х = 7). При t ∈ (-∞; 0) имеем: f(t) ≤ -10. Неравенство переходит в равенство при t = -5 (или х - 2 = -5, т. е. х = -3). Итак, 
Ответ: 
11. Запишем значение данной функции f(x) при х = 2:  Число 42 также запишем в двоичной системе счисления:
Число 42 также запишем в двоичной системе счисления: 
 Сравнивая две приведенные записи, находим: а = 1, b = 0, с = 1, d = 0, k = 1, m = 0.
Сравнивая две приведенные записи, находим: а = 1, b = 0, с = 1, d = 0, k = 1, m = 0.
Ответ: а = 1, b = 0, с = 1, d = 0, k = 1, m = 0.
12. Данное выражение запишем в виде  При этом 1 - у ≥ 0, т. е. у ≤ 1. Возведем в квадрат обе части равенства:
При этом 1 - у ≥ 0, т. е. у ≤ 1. Возведем в квадрат обе части равенства:  или
или  Выделим полный квадрат по переменной х:
Выделим полный квадрат по переменной х:  Получили уравнение окружности. С учетом ограничения у ≤ 1 имеем нижнюю полуокружность с центром в точке А(-2; 1) и радиуса R = 3.
Получили уравнение окружности. С учетом ограничения у ≤ 1 имеем нижнюю полуокружность с центром в точке А(-2; 1) и радиуса R = 3.

Ответ: график построен.
Вариант 2

3. Функция возрастает на промежутке [0; 2] и убывает на промежутке [-2; 0], 
4. Функция четная.

6. а, б построены.
7. 3,92.
8. x1 = 1 и х2 = -4/5.
9. а, б построены.
10. Разделим числитель дроби на знаменатель и выделим целую часть. Получим:  Введем новую переменную t = х + 5 и запишем функцию в виде
Введем новую переменную t = х + 5 и запишем функцию в виде  Очевидно, что эта функция нечетная. Рассмотрим промежуток t ∈ (0; +∞) и напишем неравенство для среднего арифметического и среднего геометрического. Получим:
Очевидно, что эта функция нечетная. Рассмотрим промежуток t ∈ (0; +∞) и напишем неравенство для среднего арифметического и среднего геометрического. Получим:  или
или  Неравенство переходит в равенство при t = 36/t, т. е. t = 6 (или х + 5 = 6, т. е. x = 1). При t ∈ (-∞; 0) имеем: f(t) ≤ -12. Неравенство переходит в равенство при t = -6 (или x + 5 = -6, т. е. x = -11). Итак,
Неравенство переходит в равенство при t = 36/t, т. е. t = 6 (или х + 5 = 6, т. е. x = 1). При t ∈ (-∞; 0) имеем: f(t) ≤ -12. Неравенство переходит в равенство при t = -6 (или x + 5 = -6, т. е. x = -11). Итак, 
Ответ: 
11. Запишем значение данной функции f(x) при x = 2:  Число 40 также запишем в двоичной системе счисления:
Число 40 также запишем в двоичной системе счисления: 
 Сравнивая две приведенные записи, находим: a = 1, b = 0, c= 1, d= 0, k = 0, m = 0.
Сравнивая две приведенные записи, находим: a = 1, b = 0, c= 1, d= 0, k = 0, m = 0.
Ответ: a = 1, b = 0, c= 1, d= 0, k = 0, m = 0.
12. Данное выражение запишем в виде  При этом y + 1 ≥ 0, т. е. у ≥ 1. Возведем в квадрат обе части равенства:
При этом y + 1 ≥ 0, т. е. у ≥ 1. Возведем в квадрат обе части равенства:  или
или  Выделим полный квадрат по переменной x:
Выделим полный квадрат по переменной x:  Получили уравнение окружности. С учетом ограничения у ≥ -1 имеем верхнюю полуокружность с центром в точке А(3; -1) и радиуса R = 2.
Получили уравнение окружности. С учетом ограничения у ≥ -1 имеем верхнюю полуокружность с центром в точке А(3; -1) и радиуса R = 2.

Ответ: график построен.
Просмотр содержимого документа
«Тема урока: Зачетная работа по теме «Числовые функции»»
План урока
Предмет: математика
Преподаватель: Амирханова А. К.
Дата проведении:__________
Тема урока: Зачетная работа по теме «Числовые функции»
Цель: проверить знания учащихся по вариантам одинаковой сложности.
Ход уроков
I. Сообщение темы и цели уроков
II. Характеристика зачетной работы
Работа составлена в двух равноценных вариантах. По сравнению с контрольной работой увеличено количество заданий. Соответственно, у учащихся появляется возможность выбора задач. Все задания разбиты на три части: А, В и С. Самые простые задачи находятся в части А, более сложные - в части В, еще сложнее - в части С. Каждая задача из части А оценивается в 1 балл, из В - в 2 балла, из С - в 3 балла. Поэтому за правильное решение всех задач части А можно получить 7 баллов, части В - 8 баллов и части С - 9 баллов (всего 24 балла). Оценка «3» ставится за 6 баллов, оценка «4» - за 10 баллов, оценка «5» - за 14 баллов.
Так как эта работа является зачетной, то в нее не включены принципиально новые задачи. Поэтому разбору заданий работы отдельного урока можно и не посвящать (решения задач могут быть вывешены на стенде). Для стендового размещения разбор вариантов приводится.
III. Варианты зачетной работы
Вариант 1
А
1. Найдите область определения функции 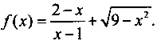
2. Определите область значений функции 
3. Найдите промежутки возрастания и убывания функции  ее наибольшее и наименьшее значения.
ее наибольшее и наименьшее значения.
4. Определите четность или нечетность функции 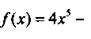
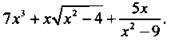
5. Найдите значение функции 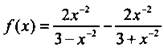 при х = 0,5-1.
при х = 0,5-1.
6. Постройте график функции:

В
7. Даны функции 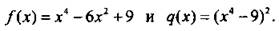 Найдите значение выражения
Найдите значение выражения  при х = -0,3.
при х = -0,3.
8. Дана функция /(х) = 4х2 - х. Решите уравнение /(/(х)) = 33.
9. Постройте график функции:

C
10. Найдите область значений функции 
11. Дана функция  где коэффициенты а, b, с, d, k, mмогут принимать значения 0 и 1. Найдите значения а, b, с, d, k, m, для которых f(2) = 42.
где коэффициенты а, b, с, d, k, mмогут принимать значения 0 и 1. Найдите значения а, b, с, d, k, m, для которых f(2) = 42.
12. Постройте график функции 
Вариант 2
1. Найдите область определения функции 
2. Определите область значений функции f(х) = 3х2 - 12х + 1.
3. Найдите промежутки возрастания и убывания функции 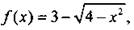 ее наибольшее и наименьшее значения.
ее наибольшее и наименьшее значения.
4. Определите четность или нечетность функции 
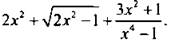
5. Найдите значение функции  при х = 0,2-1.
при х = 0,2-1.
6. Постройте график функции:
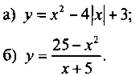
В
7. Даны функции  Найдите значение выражения
Найдите значение выражения  при х = -0,7.
при х = -0,7.
8. Дана функция f(х) = 5х2 - х. Решите уравнение f(f(х)) = 76.
9. Постройте график функции:
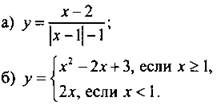
C
10. Найдите область значений функции 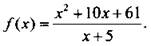
11. Дана функция 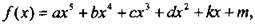 где коэффициенты а, b, с, d, k, mмогут принимать значения 0 и 1. Найдите значения а, b, с, d, k, m, для которых f(2) = 40.
где коэффициенты а, b, с, d, k, mмогут принимать значения 0 и 1. Найдите значения а, b, с, d, k, m, для которых f(2) = 40.
12. Постройте график функции 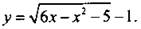
IV. Ответы и решения
Вариант 1

3. Функция возрастает на промежутке [-5; 0] и убывает на промежутке [0; 5], 
4. Функция нечетная.
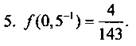
6. а, б построены.
7. 1,08.
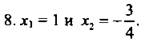
9. а, б построены.
10. Разделим числитель дроби на знаменатель и выделим целую часть. Получим:  Введем новую переменную t = х - 2 и запишем функцию в виде
Введем новую переменную t = х - 2 и запишем функцию в виде  Очевидно, что эта функция нечетная. Рассмотрим промежуток t ∈ (0; +∞) и напишем неравенство для среднего арифметического и среднего геометрического. Получим:
Очевидно, что эта функция нечетная. Рассмотрим промежуток t ∈ (0; +∞) и напишем неравенство для среднего арифметического и среднего геометрического. Получим: 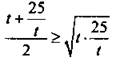 или
или 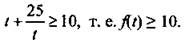 Неравенство переходит в равенство при t = 25/t, т. е. t = 5 (или х - 2 = 5, т. е. х = 7). При t ∈ (-∞; 0) имеем: f(t) ≤ -10. Неравенство переходит в равенство при t = -5 (или х - 2 = -5, т. е. х = -3). Итак,
Неравенство переходит в равенство при t = 25/t, т. е. t = 5 (или х - 2 = 5, т. е. х = 7). При t ∈ (-∞; 0) имеем: f(t) ≤ -10. Неравенство переходит в равенство при t = -5 (или х - 2 = -5, т. е. х = -3). Итак, 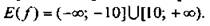
Ответ: 
11. Запишем значение данной функции f(x) при х = 2: 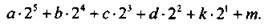 Число 42 также запишем в двоичной системе счисления:
Число 42 также запишем в двоичной системе счисления: 
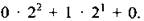 Сравнивая две приведенные записи, находим: а = 1, b = 0, с = 1, d = 0, k = 1, m = 0.
Сравнивая две приведенные записи, находим: а = 1, b = 0, с = 1, d = 0, k = 1, m = 0.
Ответ: а = 1, b = 0, с = 1, d = 0, k = 1, m = 0.
12. Данное выражение запишем в виде  При этом 1 - у ≥ 0, т. е. у ≤ 1. Возведем в квадрат обе части равенства:
При этом 1 - у ≥ 0, т. е. у ≤ 1. Возведем в квадрат обе части равенства:  или
или  Выделим полный квадрат по переменной х:
Выделим полный квадрат по переменной х:  Получили уравнение окружности. С учетом ограничения у ≤ 1 имеем нижнюю полуокружность с центром в точке А(-2; 1) и радиуса R = 3.
Получили уравнение окружности. С учетом ограничения у ≤ 1 имеем нижнюю полуокружность с центром в точке А(-2; 1) и радиуса R = 3.
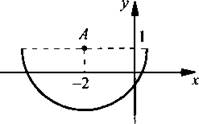
Ответ: график построен.
Вариант 2

3. Функция возрастает на промежутке [0; 2] и убывает на промежутке [-2; 0], 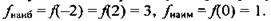
4. Функция четная.
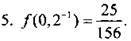
6. а, б построены.
7. 3,92.
8. x1 = 1 и х2 = -4/5.
9. а, б построены.
10. Разделим числитель дроби на знаменатель и выделим целую часть. Получим: 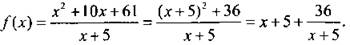 Введем новую переменную t = х + 5 и запишем функцию в виде
Введем новую переменную t = х + 5 и запишем функцию в виде 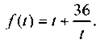 Очевидно, что эта функция нечетная. Рассмотрим промежуток t ∈ (0; +∞) и напишем неравенство для среднего арифметического и среднего геометрического. Получим:
Очевидно, что эта функция нечетная. Рассмотрим промежуток t ∈ (0; +∞) и напишем неравенство для среднего арифметического и среднего геометрического. Получим: 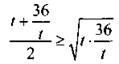 или
или  Неравенство переходит в равенство при t = 36/t, т. е. t = 6 (или х + 5 = 6, т. е. x = 1). При t ∈ (-∞; 0) имеем: f(t) ≤ -12. Неравенство переходит в равенство при t = -6 (или x + 5 = -6, т. е. x = -11). Итак,
Неравенство переходит в равенство при t = 36/t, т. е. t = 6 (или х + 5 = 6, т. е. x = 1). При t ∈ (-∞; 0) имеем: f(t) ≤ -12. Неравенство переходит в равенство при t = -6 (или x + 5 = -6, т. е. x = -11). Итак, 
Ответ: 
11. Запишем значение данной функции f(x) при x = 2: 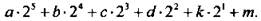 Число 40 также запишем в двоичной системе счисления:
Число 40 также запишем в двоичной системе счисления: 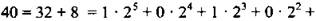
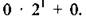 Сравнивая две приведенные записи, находим: a = 1, b = 0, c= 1, d= 0, k = 0, m = 0.
Сравнивая две приведенные записи, находим: a = 1, b = 0, c= 1, d= 0, k = 0, m = 0.
Ответ: a = 1, b = 0, c= 1, d= 0, k = 0, m = 0.
12. Данное выражение запишем в виде 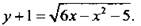 При этом y + 1 ≥ 0, т. е. у ≥ 1. Возведем в квадрат обе части равенства:
При этом y + 1 ≥ 0, т. е. у ≥ 1. Возведем в квадрат обе части равенства:  или
или 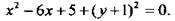 Выделим полный квадрат по переменной x:
Выделим полный квадрат по переменной x: 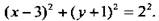 Получили уравнение окружности. С учетом ограничения у ≥ -1 имеем верхнюю полуокружность с центром в точке А(3; -1) и радиуса R = 2.
Получили уравнение окружности. С учетом ограничения у ≥ -1 имеем верхнюю полуокружность с центром в точке А(3; -1) и радиуса R = 2.

Ответ: график построен.








 ее наибольшее и наименьшее значения.
ее наибольшее и наименьшее значения.

 при х = 0,5-1.
при х = 0,5-1.
 Найдите значение выражения
Найдите значение выражения  при х = -0,3.
при х = -0,3.

 где коэффициенты а, b, с, d, k, mмогут принимать значения 0 и 1. Найдите значения а, b, с, d, k, m, для которых f(2) = 42.
где коэффициенты а, b, с, d, k, mмогут принимать значения 0 и 1. Найдите значения а, b, с, d, k, m, для которых f(2) = 42.

 ее наибольшее и наименьшее значения.
ее наибольшее и наименьшее значения.

 при х = 0,2-1.
при х = 0,2-1.
 Найдите значение выражения
Найдите значение выражения  при х = -0,7.
при х = -0,7.

 где коэффициенты а, b, с, d, k, mмогут принимать значения 0 и 1. Найдите значения а, b, с, d, k, m, для которых f(2) = 40.
где коэффициенты а, b, с, d, k, mмогут принимать значения 0 и 1. Найдите значения а, b, с, d, k, m, для которых f(2) = 40.




 Введем новую переменную t = х - 2 и запишем функцию в виде
Введем новую переменную t = х - 2 и запишем функцию в виде  Очевидно, что эта функция нечетная. Рассмотрим промежуток t ∈ (0; +∞) и напишем неравенство для среднего арифметического и среднего геометрического. Получим:
Очевидно, что эта функция нечетная. Рассмотрим промежуток t ∈ (0; +∞) и напишем неравенство для среднего арифметического и среднего геометрического. Получим:  или
или  Неравенство переходит в равенство при t = 25/t, т. е. t = 5 (или х - 2 = 5, т. е. х = 7). При t ∈ (-∞; 0) имеем: f(t) ≤ -10. Неравенство переходит в равенство при t = -5 (или х - 2 = -5, т. е. х = -3). Итак,
Неравенство переходит в равенство при t = 25/t, т. е. t = 5 (или х - 2 = 5, т. е. х = 7). При t ∈ (-∞; 0) имеем: f(t) ≤ -10. Неравенство переходит в равенство при t = -5 (или х - 2 = -5, т. е. х = -3). Итак, 

 Число 42 также запишем в двоичной системе счисления:
Число 42 также запишем в двоичной системе счисления: 
 Сравнивая две приведенные записи, находим: а = 1, b = 0, с = 1, d = 0, k = 1, m = 0.
Сравнивая две приведенные записи, находим: а = 1, b = 0, с = 1, d = 0, k = 1, m = 0. При этом 1 - у ≥ 0, т. е. у ≤ 1. Возведем в квадрат обе части равенства:
При этом 1 - у ≥ 0, т. е. у ≤ 1. Возведем в квадрат обе части равенства:  или
или  Выделим полный квадрат по переменной х:
Выделим полный квадрат по переменной х:  Получили уравнение окружности. С учетом ограничения у ≤ 1 имеем нижнюю полуокружность с центром в точке А(-2; 1) и радиуса R = 3.
Получили уравнение окружности. С учетом ограничения у ≤ 1 имеем нижнюю полуокружность с центром в точке А(-2; 1) и радиуса R = 3.



 Введем новую переменную t = х + 5 и запишем функцию в виде
Введем новую переменную t = х + 5 и запишем функцию в виде  Очевидно, что эта функция нечетная. Рассмотрим промежуток t ∈ (0; +∞) и напишем неравенство для среднего арифметического и среднего геометрического. Получим:
Очевидно, что эта функция нечетная. Рассмотрим промежуток t ∈ (0; +∞) и напишем неравенство для среднего арифметического и среднего геометрического. Получим:  или
или  Неравенство переходит в равенство при t = 36/t, т. е. t = 6 (или х + 5 = 6, т. е. x = 1). При t ∈ (-∞; 0) имеем: f(t) ≤ -12. Неравенство переходит в равенство при t = -6 (или x + 5 = -6, т. е. x = -11). Итак,
Неравенство переходит в равенство при t = 36/t, т. е. t = 6 (или х + 5 = 6, т. е. x = 1). При t ∈ (-∞; 0) имеем: f(t) ≤ -12. Неравенство переходит в равенство при t = -6 (или x + 5 = -6, т. е. x = -11). Итак, 
 Число 40 также запишем в двоичной системе счисления:
Число 40 также запишем в двоичной системе счисления: 
 Сравнивая две приведенные записи, находим: a = 1, b = 0, c= 1, d= 0, k = 0, m = 0.
Сравнивая две приведенные записи, находим: a = 1, b = 0, c= 1, d= 0, k = 0, m = 0. При этом y + 1 ≥ 0, т. е. у ≥ 1. Возведем в квадрат обе части равенства:
При этом y + 1 ≥ 0, т. е. у ≥ 1. Возведем в квадрат обе части равенства:  или
или  Выделим полный квадрат по переменной x:
Выделим полный квадрат по переменной x:  Получили уравнение окружности. С учетом ограничения у ≥ -1 имеем верхнюю полуокружность с центром в точке А(3; -1) и радиуса R = 2.
Получили уравнение окружности. С учетом ограничения у ≥ -1 имеем верхнюю полуокружность с центром в точке А(3; -1) и радиуса R = 2.
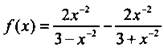 при х = 0,5-1.
при х = 0,5-1.

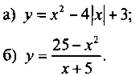
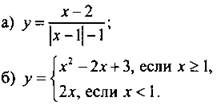
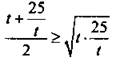 или
или 
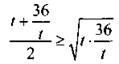 или
или 










