Теорема Менелая и теорема Чевы в школьном курсе математики

Теорема Менелая и теорема Чевы в школьном курсе математики

«Все незначительное нужно,

Чтобы значительному быть…»

И. Северянин

Содержание

Теоретические основы

• Теорема Чевы
• Теорема Менелая

Методические рекомендации

• Методика обучения решению задач в период предпрофильной подготовки
• Изучение темы «Теорема Менелая и теорема Чевы» в курсе геометрии 10 класса
• Применение теорем Менелая и Чевы в решении стереометрических задач

Теорема Чевы

• Пусть в ∆ ABC на сторонах BC,AC,AB или их продолжениях взяты соответственно точки A 1 , B 1 и C 1 ,не совпадающие с вершинами треугольника. Прямые A A 1 , BB 1 и CC 1 пересекаются в одной точке или параллельны тогда и только тогда, когда выполняется равенство

Теорема Менелая

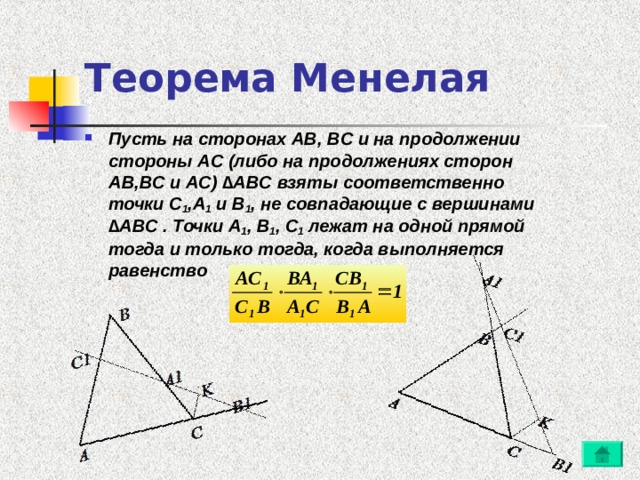
• Пусть на сторонах AB, BC и на продолжении стороны AC (либо на продолжениях сторон AB,BC и AC) ∆ABC взяты соответственно точки C 1 ,A 1 и B 1 , не совпадающие с вершинами ∆ABC . Точки A 1 , B 1 , C 1 лежат на одной прямой тогда и только тогда, когда выполняется равенство

Методика обучения решению задач в период предпрофильной подготовки

• 1. Теорема Менелая и пропорциональные отрезки в треугольнике.
• 2. Теорема Чевы и ее следствия. Применение теорем Чевы и Менелая к задачам на доказательство.
• 3. Решение задач на пропорциональное деление отрезков в треугольнике.
• 4. Решение задач, связанных с нахождением площадей.
• 5. Комбинированные задачи.

Теорема Менелая и пропорциональные отрезки в треугольнике

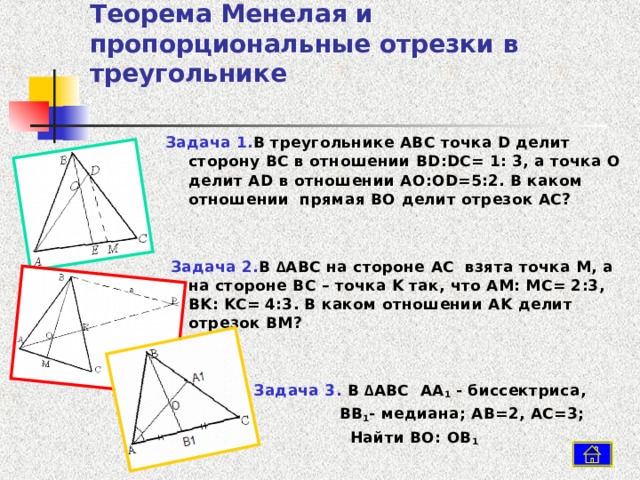
Задача 1. В треугольнике ABC точка D делит сторону BC в отношении BD : DC = 1: 3, а точка O делит AD в отношении AO : OD =5:2. В каком отношении прямая BO делит отрезок AC?

Задача 2. В ∆ ABC на стороне AC взята точка M , а на стороне BC – точка K так, что AM : MC = 2:3, BK : KC = 4:3. В каком отношении AK делит отрезок BM ?

Задача 3. В ∆ ABC AA 1 - биссектриса,

BB 1 - медиана; AB =2, AC =3;

Найти BO : OB 1

Теорема Чевы и ее следствия.

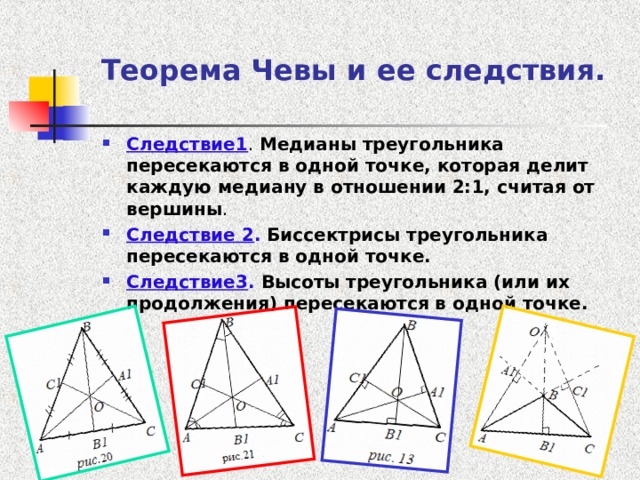
• Следствие1 . Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины .
• Следствие 2 . Биссектрисы треугольника пересекаются в одной точке.
• Следствие3 . Высоты треугольника (или их продолжения) пересекаются в одной точке.

Теорема Чевы и ее следствия.

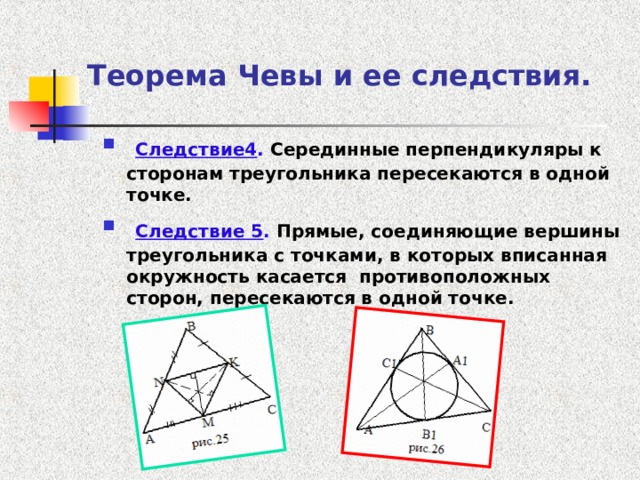
• Следствие4 . Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
• Следствие 5 . Прямые, соединяющие вершины треугольника с точками, в которых вписанная окружность касается противоположных сторон, пересекаются в одной точке.

Применение теорем Чевы и Менелая к задачам на доказательство

• Задача 1 . Используя теорему Чевы, доказать, что в произвольном треугольнике прямые, проходящие через вершины и делящие периметр треугольника пополам, пересекаются в одной точке.

• Задача 2. На стороне AC треугольника ABC взяты точки P и E , на стороне BC – точки M и K , причем AP : PE : EC = CK : KM : MB . Отрезки AM и BP пересекаются в точке O , отрезки AK и BE – в точке T . Докажите, что точки O , T и С лежат на одной прямой.

Задачи на пропорциональное деление отрезков в треугольнике.

• Задача 1. В треугольнике ABC , описанном около окружности, AB = 8, BC = 5, AC = 4. Точки A 1 ,В 1 и C 1 - точки касания, принадлежащие соответственно сторонам BC , AC и BA . Точка P - точка пересечения отрезков AA 1 и CC 1 . Найдите AP:PA 1 .
• Задача 2. Стороны треугольника 5, 6 и 7. Найдите отношение отрезков, на которые биссектриса большего угла этого треугольника разделена центром окружности, вписанной в треугольник.

Задачи на пропорциональное деление отрезков в треугольнике.

• Задача 3. В треугольнике ABC , площадь которого равна 6, на стороне AB взята точка K , делящая эту сторону в отношении AK : BK = 2:3, а на стороне AC – точка L , делящая AC в отношении AL : LC = 5:3. Точка Q пересечения прямых CK и BL удалена от прямой AB на расстояние 1,5. Найдите длину стороны AB .

• Задача 4. На стороне AC в треугольнике ABC взята точка K . AK =1, KC = 3. На стороне AB взята точка L . AL : LB =2:3. Q – точка пересечения прямых BK и CL . S = 1. Найдите длину высоты треугольника ABC , опущенной из вершины B .

Задачи, связанные с нахождением площадей

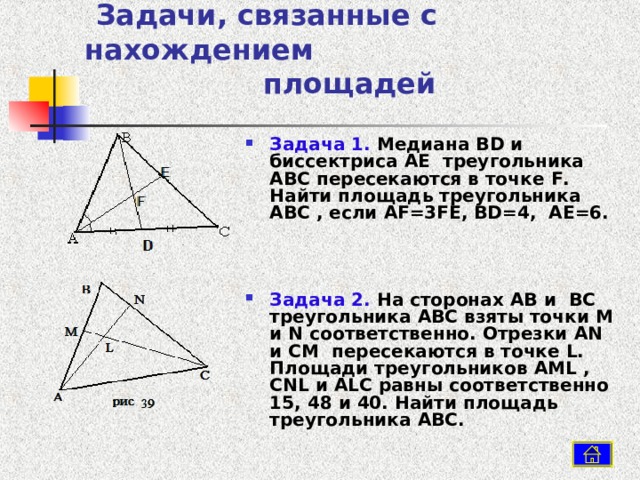
• Задача 1. Медиана BD и биссектриса AE треугольника ABC пересекаются в точке F . Найти площадь треугольника ABC , если AF =3 FE , BD =4, AE =6.

• Задача 2. На сторонах AB и BC треугольника ABC взяты точки M и N соответственно. Отрезки AN и CM пересекаются в точке L . Площади треугольников AML , CNL и ALC равны соответственно 15, 48 и 40. Найти площадь треугольника ABC .

Комбинированные задачи.

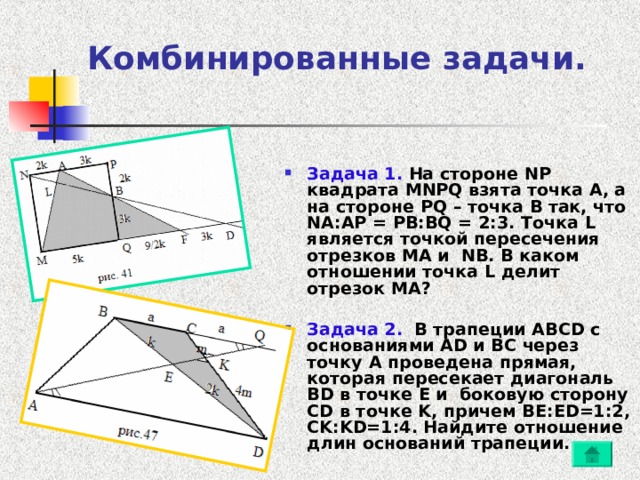
• Задача 1. На стороне NP квадрата MNPQ взята точка A , а на стороне PQ – точка B так, что NA : AP = PB : BQ = 2:3. Точка L является точкой пересечения отрезков MA и NB . В каком отношении точка L делит отрезок MA ?

• Задача 2. В трапеции ABCD с основаниями AD и BC через точку A проведена прямая, которая пересекает диагональ BD в точке E и боковую сторону CD в точке K , причем BE : ED =1:2, CK : KD =1:4. Найдите отношение длин оснований трапеции.

Изучение темы «Теорема Менелая и теорема Чевы» в курсе геометрии 10 класса

Урок 1. Теорема Менелая и теорема Чевы.

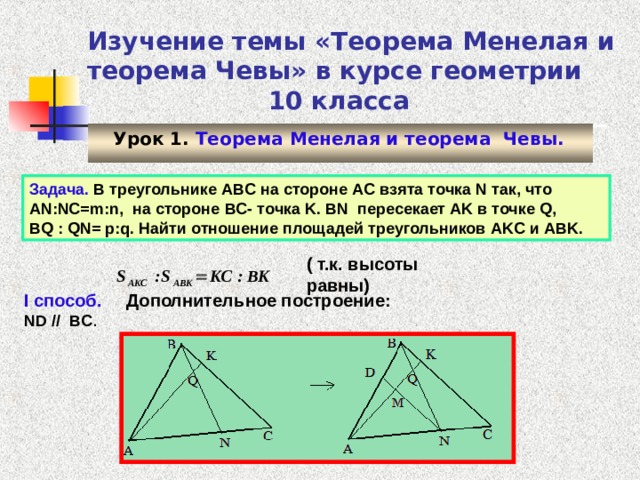
Задача. В треугольнике ABC на стороне AC взята точка N так, что AN : NC = m : n , на стороне BC - точка K . BN пересекает AK в точке Q ,

BQ : QN = p : q . Найти отношение площадей треугольников AKC и ABK .

( т.к. высоты равны)

I способ. Дополнительное построение: ND //

BC .

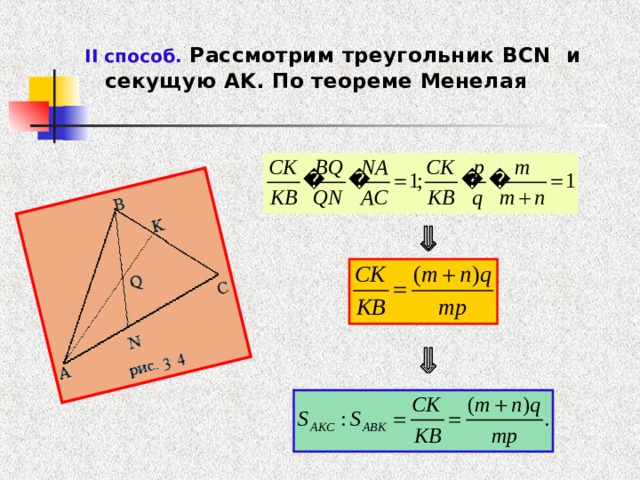
II способ. Рассмотрим треугольник BCN и секущую AK. По теореме Менелая

Изучение темы «Теорема Менелая

и теорема Чевы» в курсе геометрии 10 класса

Урок 2. Применение теорем Менелая и Чевы в решении ключевых задач

Цели урока: 1) формировать умения:

-видеть конфигурации, удовлетворяющие

заданным условиям;

-решать задачи нестандартными

способами;

-использовать теоремы в задачах на

доказательство;

2) развивать самостоятельность.

Задача. В равнобедренном треугольнике ABC ( A С= BC ) проведены медиана BN и высота АМ, которые пересекаются в точке D . AD =5, DM =2. Найти

Решение : AN = NC , AM =5+2=7. Рассмотрим ∆AMC и секущую NB. По теореме Менелая

,

,

;

Пусть коэффициент пропорциональности равен k , тогда СМ=3 k , BM =2 k . Из ∆ ACM- прямоугольного:

Ответ :

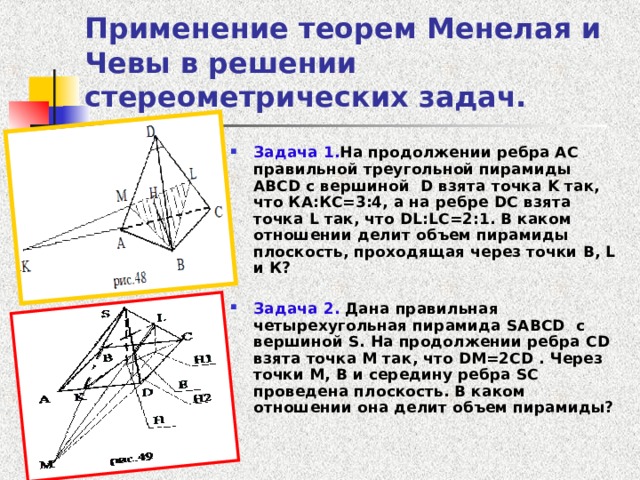
Применение теорем Менелая и Чевы в решении стереометрических задач.

• Задача 1. На продолжении ребра АС правильной треугольной пирамиды ABCD с вершиной D взята точка K так, что КА:КС=3:4, а на ребре DC взята точка L так, что DL : LC =2:1. В каком отношении делит объем пирамиды плоскость, проходящая через точки B , L и К?
• Задача 2. Дана правильная четырехугольная пирамида SABCD с вершиной S . На продолжении ребра CD взята точка M так, что DM=2CD . Через точки М, В и середину ребра SC проведена плоскость. В каком отношении она делит объем пирамиды?

Применение теорем Менелая и Чевы в решении стереометрических задач.

• Задача 3. Дана правильная треугольная призма с боковыми ребрами AA 1 , BB 1 и CC 1 . Причем на продолжении ребра BA взята точка M так, что MA=AB . Через точки M,B 1 и середину ребра AC проведена плоскость. В каком отношении она делит объем призмы?

«Умение решать задачи- такое же практическое искусство, как умение плавать или бегать. Ему можно научиться только путем подражания или упражнения» Д.Пойа