Теоремаи Пифагор. Масъалаҳо.

ТРЕНАЖЕРИ МАТЕМАТИКӢ

«Теоремаи Пифагора»

3

5

6

1

2

4

9

8

7

10

11

12

13

14

15

16

1

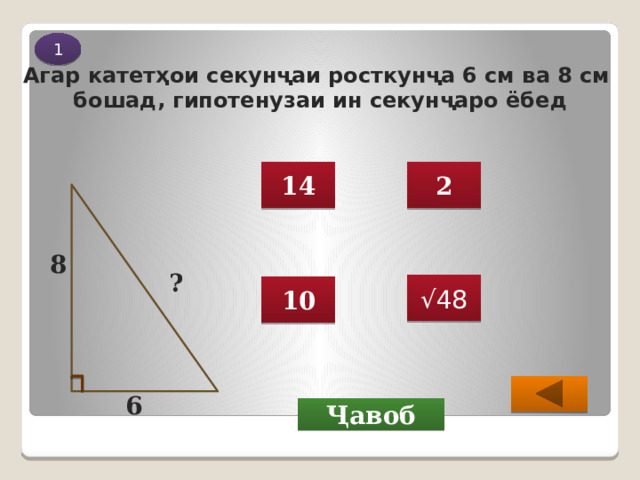
Агар катетҳои секунҷаи росткунҷа 6 см ва 8 см

бошад, гипотенузаи ин секунҷаро ёбед

14

2

8

?

√ 48

10

6

Ҷавоб

1

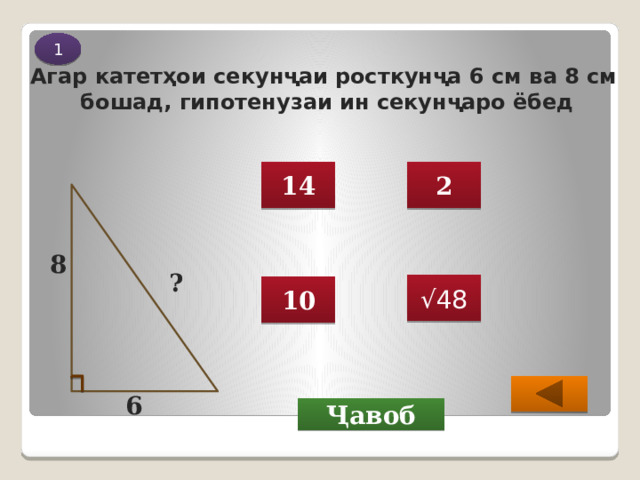
Агар катетҳои секунҷаи росткунҷа 6 см ва 8 см

бошад, гипотенузаи ин секунҷаро ёбед

14

2

8

?

√ 48

10

6

Ҷавоб

2

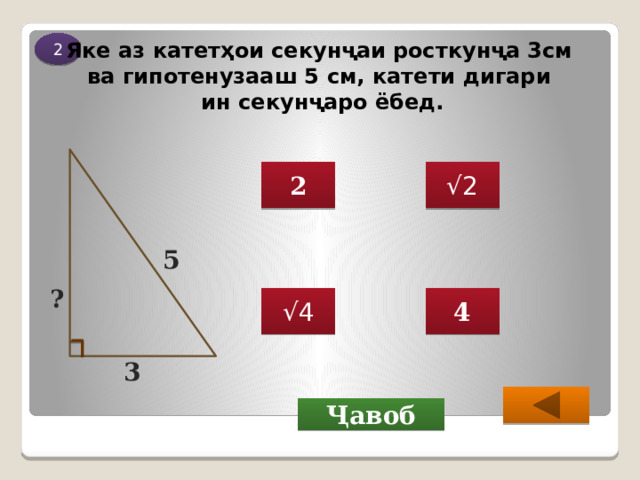
Яке аз катетҳои секунҷаи росткунҷа 3см

ва гипотенузааш 5 см, катети дигари

ин секунҷаро ёбед.

2

√ 2

5

?

√ 4

4

3

Ҷавоб

3

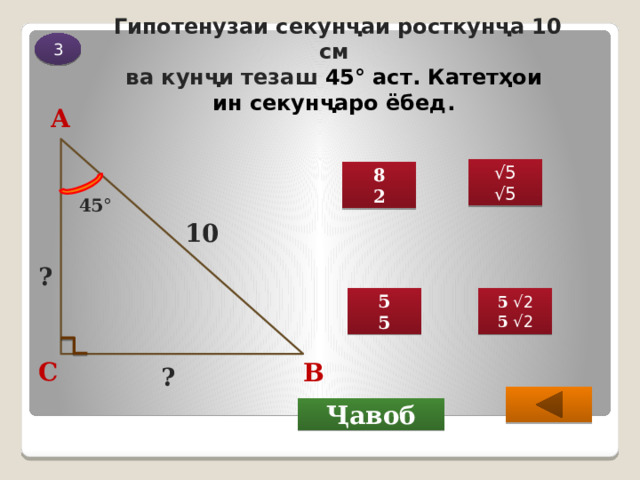
Гипотенузаи секунҷаи росткунҷа 10 см ва кунҷи тезаш 45° аст. Катетҳои ин секунҷаро ёбед.

А

√ 5

√ 5

8

2

45 °

10

?

5 √2

5

5 √2

5

С

В

?

Ҷавоб

4

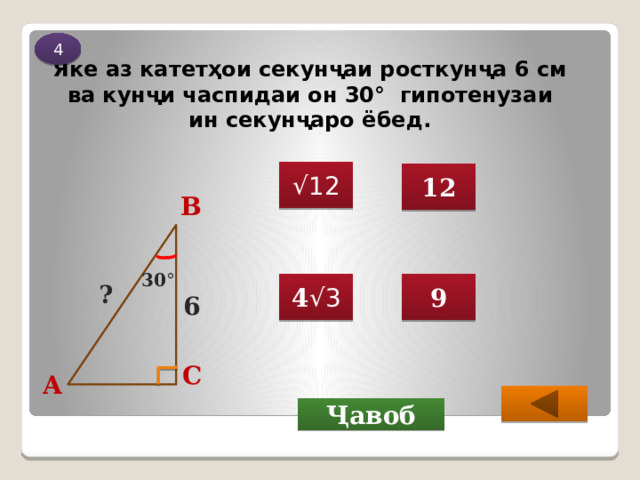
Яке аз катетҳои секунҷаи росткунҷа 6 см ва кунҷи часпидаи он 30° гипотенузаи ин секунҷаро ёбед.

√ 12

12

В

30 °

9

4 √3

?

6

С

А

Ҷавоб

5

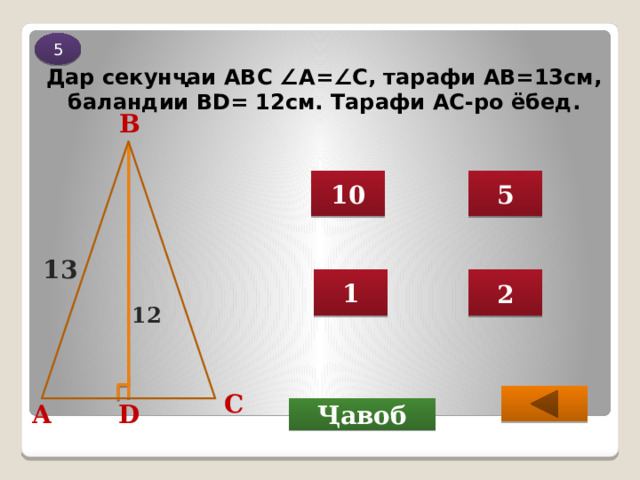
Дар секунҷаи АВС ∠А=∠С, тарафи АВ=13см, баландии ВD= 12см. Тарафи АС-ро ёбед.

B

10

5

13

1

2

12

C

D

А

Ҷавоб

6

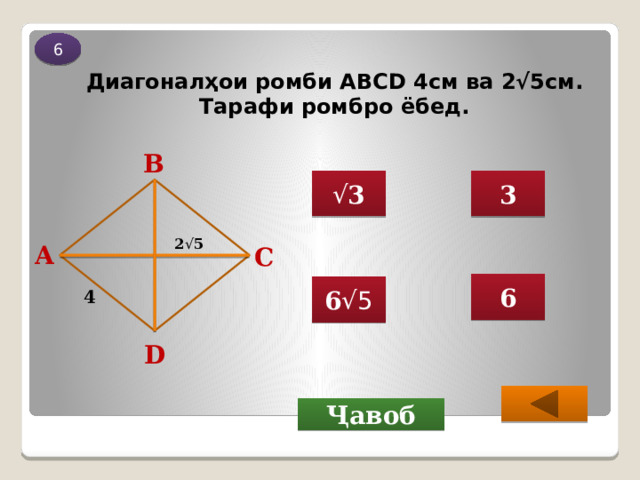
Диагоналҳои ромби ABCD 4см ва 2√5см. Тарафи ромбро ёбед.

В

3

√ 3

2 √ 5

А

С

6

6 √5

4

D

Ҷавоб

7

Кадоме секунҷаҳо бо тарафҳои:

1, 1, √2

3, 4, 5

4, 6 ,7

9, 12, 15

Секунҷаҳои «пифагорӣ» нестанд?

Ҷавоб

8

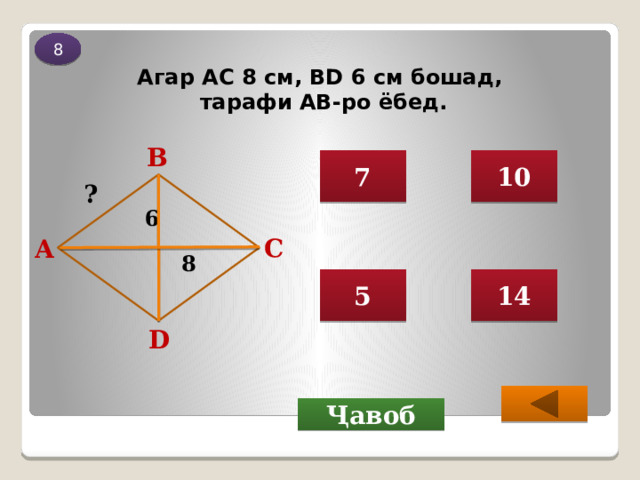
Агар АС 8 см, BD 6 см бошад, тарафи АВ-ро ёбед.

В

7

10

?

6

С

А

8

5

14

D

Ҷавоб

9

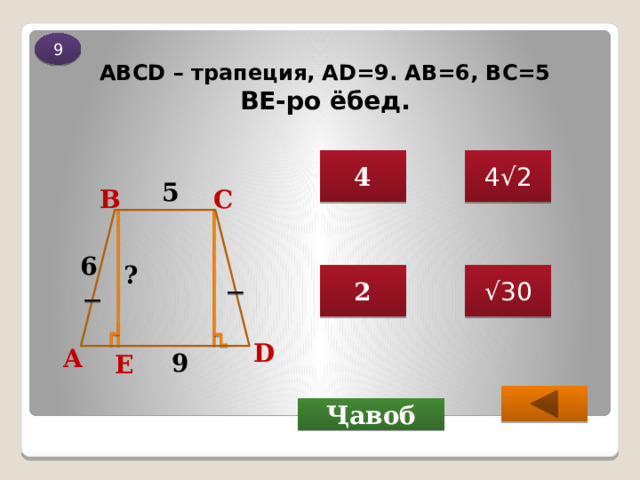
ABCD – трапеция, AD=9. АВ=6, ВС=5 ВЕ-ро ёбед.

4

4√2

5

В

С

6

?

2

√ 30

D

А

9

Е

Ҷавоб

10

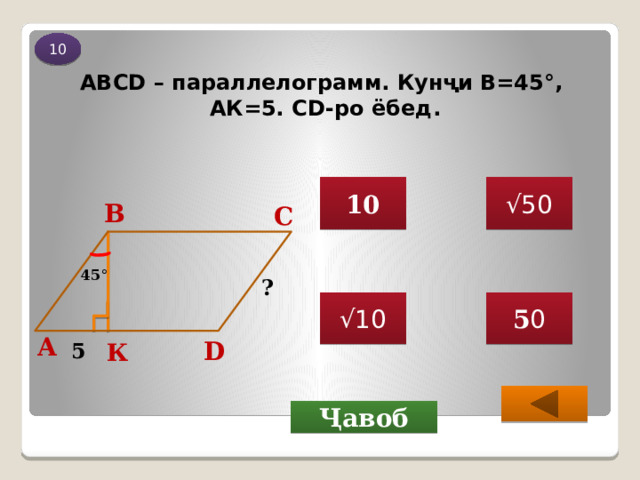
ABCD – параллелограмм. Кунҷи В=45°, AК=5. CD-ро ёбед.

10

√ 50

В

С

45 °

?

√ 10

5 0

А

D

5

К

Ҷавоб

11

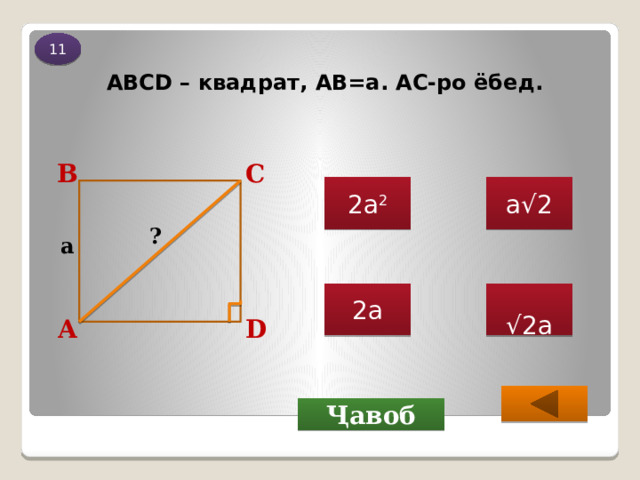
ABCD – квадрат, АВ=а. АС-ро ёбед.

В

С

2а 2

а√2

?

a

√ 2а

2а

D

А

Ҷавоб

12

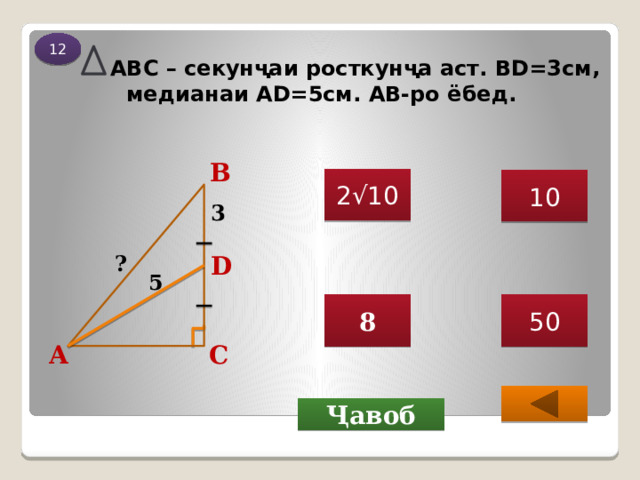
АВС – секунҷаи росткунҷа аст. BD=3см, медианаи AD=5см. АВ-ро ёбед.

В

2√10

10

3

D

?

5

50

8

С

А

Ҷавоб

13

ABC – секунҷаи росткунҷа аст. АВ= b , BC= a , АС=с -ро ҳамин тавр ёфтан мумкин:

√ а 2 - b 2

а 2 + b 2

a + b

√ а 2 + b 2

Ҷавоб

14

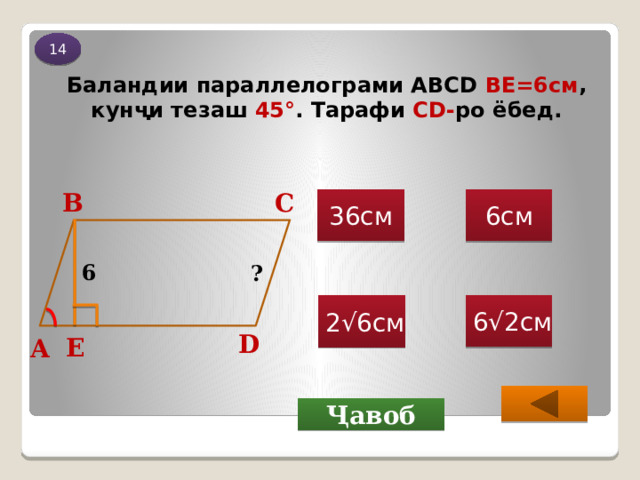
Баландии параллелограми ABCD ВЕ=6см , кунҷи тезаш 45 ° . Тарафи СD- ро ёбед.

В

С

36см

6см

6

?

6√2см

2√6см

D

Е

А

Ҷавоб

15

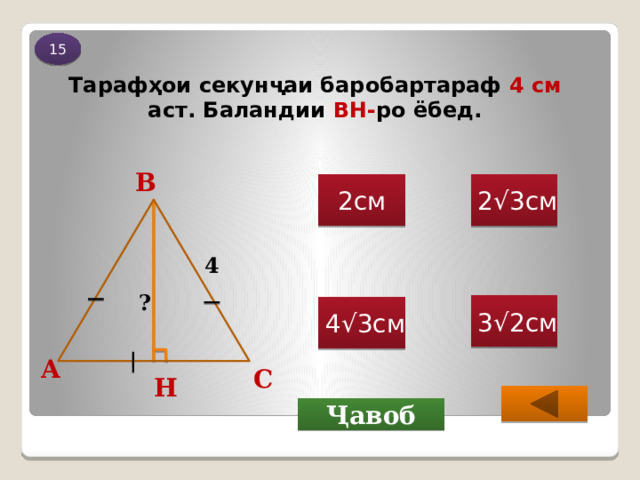
Тарафҳои секунҷаи баробартараф 4 см аст. Баландии BH- ро ёбед.

В

2√3см

2см

4

?

3√2см

4√3см

А

С

Н

Ҷавоб

16

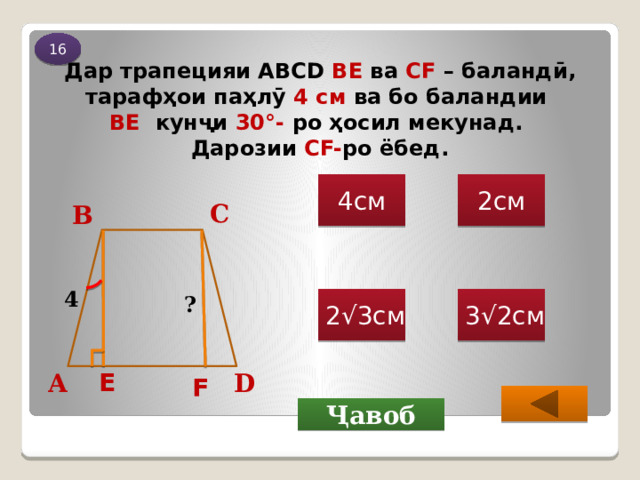
Дар трапецияи ABCD ВЕ ва СF – баландӣ, тарафҳои паҳлӯ 4 см ва бо баландии BE кунҷи 30 °- ро ҳосил мекунад . Дарозии CF- ро ёбед.

2см

4см

С

В

4

?

2√3см

3√2см

Е

D

А

F

Ҷавоб

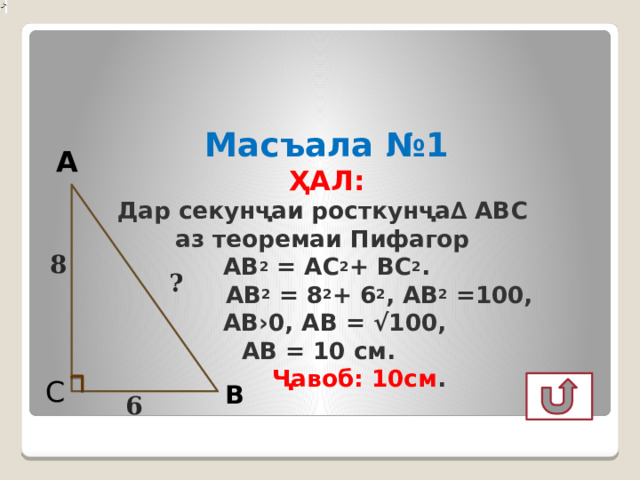
Масъала №1 ҲАЛ: Дар секунҷаи росткунҷа∆ АВС аз теоремаи Пифагор АВ 2 = АС 2 + ВС 2 . АВ 2 = 8 2 + 6 2 , АВ 2 =100, АВ›0, АВ = √100, АВ = 10 см. Ҷавоб: 10см .

А

8

?

С

В

6

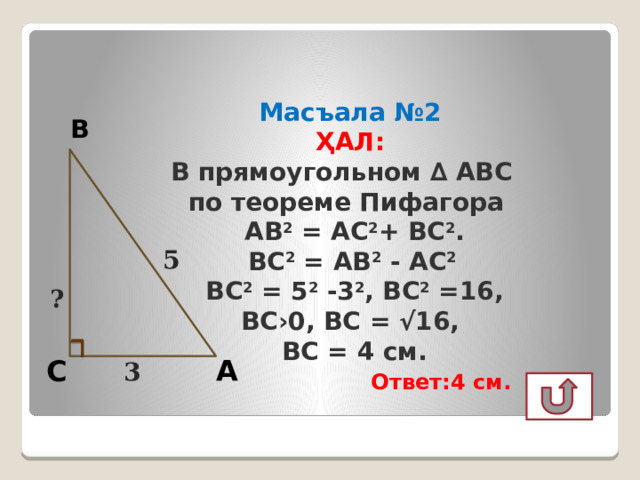
Масъала №2 ҲАЛ: В прямоугольном ∆ АВС по теореме Пифагора АВ 2 = АС 2 + ВС 2 . ВС 2 = АВ 2 - АС 2 ВС 2 = 5 2 -3 2 , ВС 2 =16, ВС›0, ВС = √16, ВС = 4 см. Ответ:4 см.

В

5

?

А

С

3

Масъала №3

ҲАЛ:

Агар  А =45 0 бошад, он гоҳ

 В=90 0 -45 0 =45 0 (дар секунҷаи росткунҷа суммаи кунҷҳои тез 90 0 аст). Ду кунҷи

∆ АВС баробаранд, яъне ин секунҷа баробарпаҳлӯ аст, АС = ВС.

Дар секунҷаи росткунҷаи АВС бо мувофиқи теоремаи Пифагор:

АВ 2 = АС 2 + ВС 2

100= 2 АС 2 , АС 2 = 50, АС›0,

АС = ВС = √ 50 = 5 √2(см)

Ҷавоб: 5√2см, 5√2см

А

45 °

10

?

?

В

С

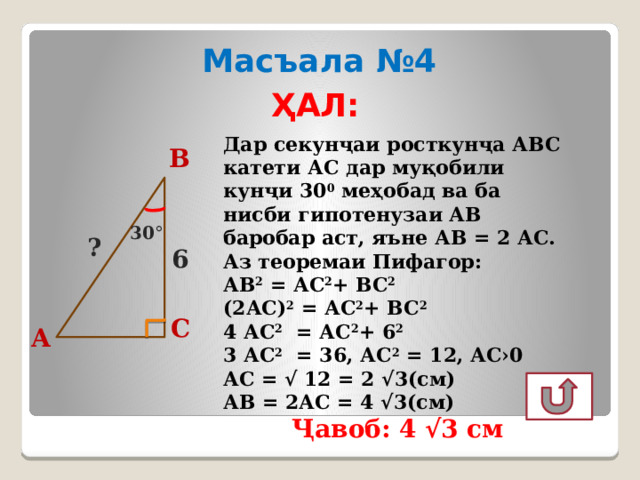
Масъала №4

ҲАЛ:

Дар секунҷаи росткунҷа АВС катети АС дар муқобили кунҷи 30 0 меҳобад ва ба нисби гипотенузаи АВ баробар аст, яъне АВ = 2 АС.

Аз теоремаи Пифагор:

АВ 2 = АС 2 + ВС 2

(2АС) 2 = АС 2 + ВС 2

4 АС 2 = АС 2 + 6 2

3 АС 2 = 36, АС 2 = 12, АС›0

АС = √ 12 = 2 √3(см)

АВ = 2АС = 4 √3(см)

Ҷавоб: 4 √3 см

В

30 °

?

6

С

А

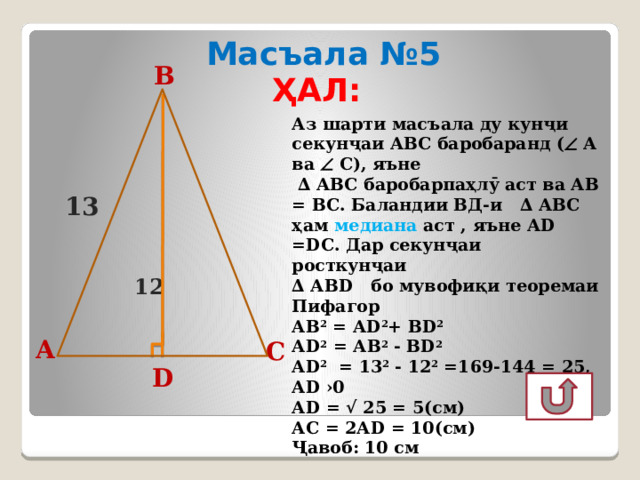
Масъала №5

ҲАЛ:

B

Аз шарти масъала ду кунҷи секунҷаи АВС баробаранд (  А ва  С), яъне

∆ АВС баробарпаҳлӯ аст ва АВ = ВС. Баландии ВД-и ∆ АВС ҳам медиана аст , яъне АD =DС. Дар секунҷаи росткунҷаи

∆ АВD бо мувофиқи теоремаи Пифагор

АВ 2 = АD 2 + ВD 2

АD 2 = АB 2 - ВD 2

АD 2 = 13 2 - 12 2 =169-144 = 25, АD ›0

АD = √ 25 = 5(см)

АC = 2АD = 10(см)

Ҷавоб: 10 см

13

12

А

C

D

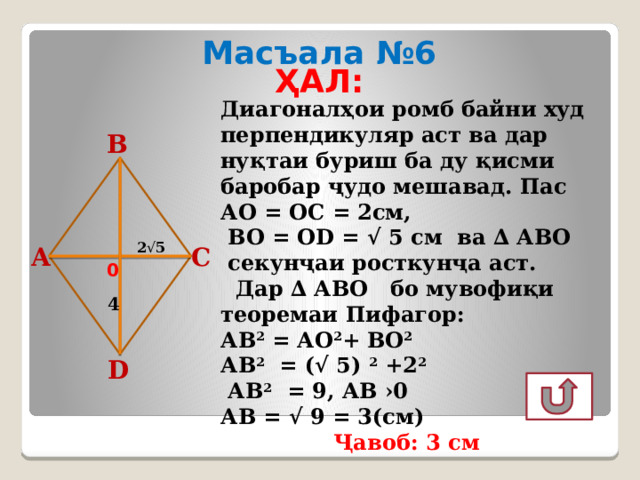
Масъала №6

ҲАЛ:

Диагоналҳои ромб байни худ перпендикуляр аст ва дар нуқтаи буриш ба ду қисми баробар ҷудо мешавад. Пас АО = ОС = 2см,

ВО = ОD = √ 5 см ва ∆ АВО

секунҷаи росткунҷа аст.

Дар ∆ АВО бо мувофиқи

теоремаи Пифагор:

АВ 2 = АО 2 + ВО 2

АВ 2 = (√ 5) 2 +2 2

АВ 2 = 9, АВ ›0

АВ = √ 9 = 3(см)

Ҷавоб: 3 см

В

2 √ 5

А

С

0

4

D

Масъала №7

ҲАЛ:

Ҷавоби дуруст: 4, 6, 7.

Дархақиқат,

4² + 6² = 52 ≠ 49 = 7².

Қайд кардан зарур аст, ки

дар замонаҳои Пифагор ҷавоби

А) ҳам дуруст ба ҳисоб мерафт

чунки ададҳои ратсионалӣ ва

ирратсионалӣ номаълум буданд.

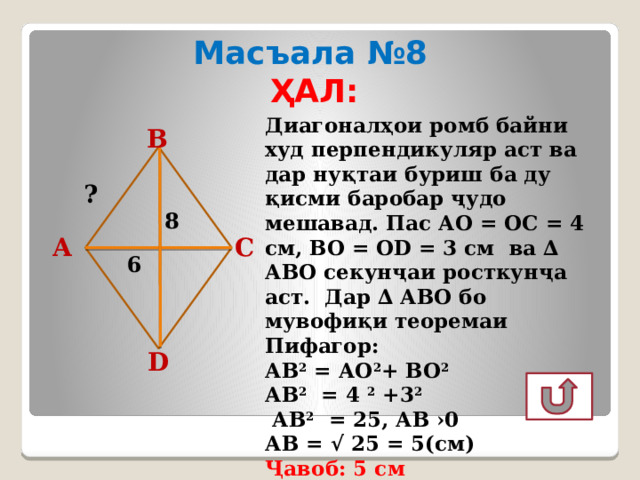
Масъала №8

ҲАЛ:

Диагоналҳои ромб байни худ перпендикуляр аст ва дар нуқтаи буриш ба ду қисми баробар ҷудо мешавад. Пас АО = ОС = 4 см, ВО = ОD = 3 см ва ∆ АВО секунҷаи росткунҷа аст. Дар ∆ АВО бо мувофиқи теоремаи Пифагор:

АВ 2 = АО 2 + ВО 2

АВ 2 = 4 2 +3 2

АВ 2 = 25, АВ ›0

АВ = √ 25 = 5(см)

Ҷавоб: 5 см

В

?

8

А

С

6

D

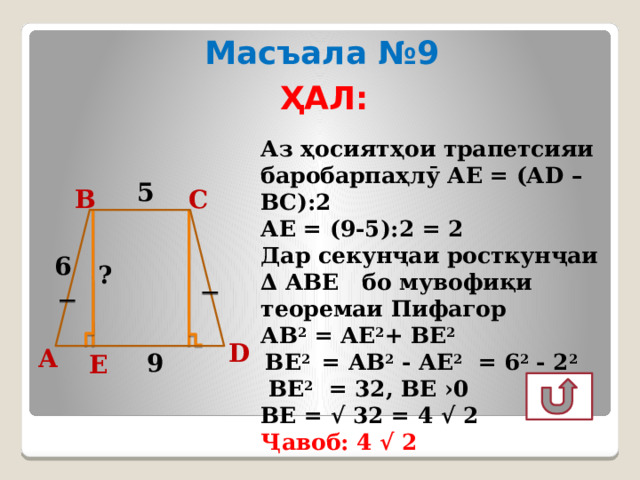
Масъала №9

ҲАЛ:

Аз ҳосиятҳои трапетсияи баробарпаҳлӯ АЕ = (АD – ВС):2

АЕ = (9-5):2 = 2

Дар секунҷаи росткунҷаи ∆ АВЕ бо мувофиқи теоремаи Пифагор

АВ 2 = АЕ 2 + ВЕ 2

ВЕ 2 = АB 2 - АЕ 2 = 6 2 - 2 2

ВЕ 2 = 32, ВЕ ›0

ВЕ = √ 32 = 4 √ 2

Ҷавоб: 4 √ 2

5

С

В

6

?

D

А

9

Е

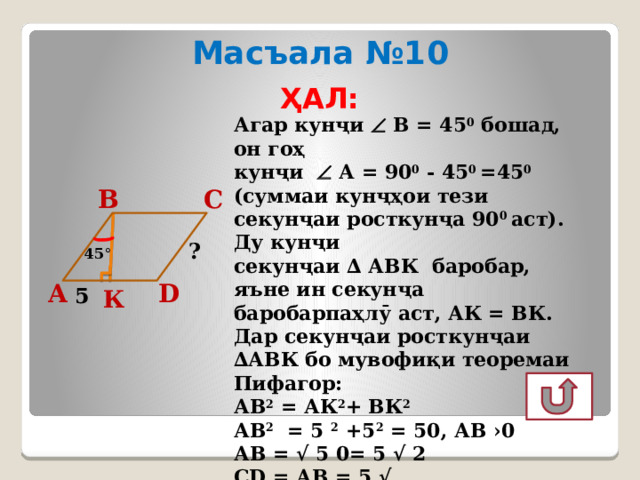
Масъала №10

ҲАЛ:

Агар кунҷи  В = 45 0 бошад, он гоҳ

кунҷи  А = 90 0 - 45 0 =45 0

(суммаи кунҷҳои тези секунҷаи росткунҷа 90 0 аст). Ду кунҷи

секунҷаи ∆ АВК баробар, яъне ин секунҷа баробарпаҳлӯ аст, АК = ВК.

Дар секунҷаи росткунҷаи ∆АВК бо мувофиқи теоремаи Пифагор:

АВ 2 = АК 2 + ВК 2

АВ 2 = 5 2 +5 2 = 50, АВ ›0

АВ = √ 5 0= 5 √ 2

CD = АВ = 5 √

Ҷавоб: 5 √ 2

С

В

?

45 °

А

D

5

К

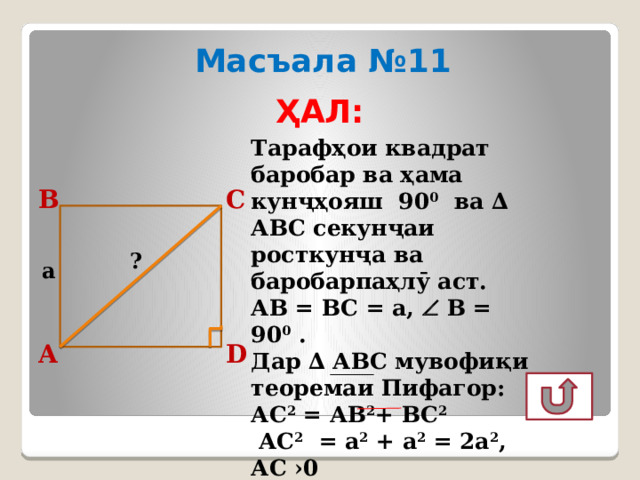
Масъала №11

ҲАЛ:

Тарафҳои квадрат баробар ва ҳама кунҷҳояш 90 0 ва ∆ АВС секунҷаи росткунҷа ва баробарпаҳлӯ аст.

АВ = ВС = а,  В = 90 0 .

Дар ∆ АВС мувофиқи

теоремаи Пифагор:

АС 2 = АВ 2 + ВС 2

АС 2 = а 2 + а 2 = 2а 2 , АС ›0

АС = а √ 2

Ҷавоб: а √ 2

С

В

?

a

D

А

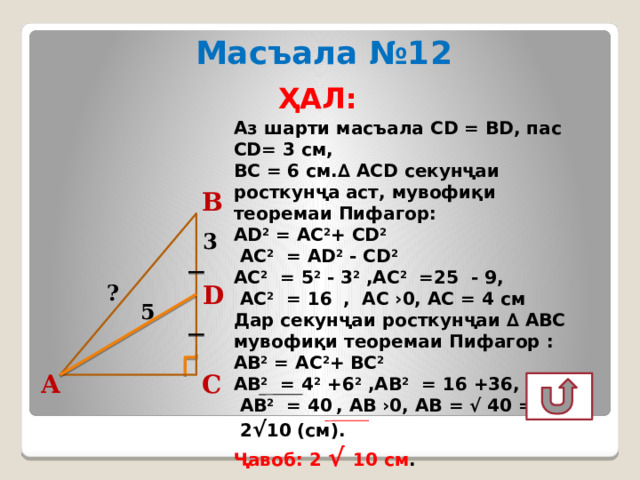
Масъала №12

ҲАЛ:

Аз шарти масъала CD = BD, пас CD= 3 см,

ВС = 6 см.∆ АCD секунҷаи росткунҷа аст, мувофиқи теоремаи Пифагор:

АD 2 = АC 2 + СD 2

АС 2 = AD 2 - CD 2

АС 2 = 5 2 - 3 2 ,АС 2 =25 - 9,

АС 2 = 16 , АС ›0, АС = 4 см

Дар секунҷаи росткунҷаи ∆ АВС мувофиқи теоремаи Пифагор :

АВ 2 = АC 2 + ВС 2

АВ 2 = 4 2 +6 2 ,АВ 2 = 16 +36,

АВ 2 = 40 , АВ ›0, АВ = √ 40 =

2 √ 10 (см).

Ҷавоб: 2 √ 10 см .

В

3

?

D

5

С

А

Масъала №13

ҲАЛ:

Дар секунҷаи росткунҷа ∆ АВС мувофиқи теоремаи Пифагор: АВ 2 = АС 2 + ВС 2

АВ 2 = а 2 + в 2

АВ ›0

АВ = √ а 2 + в 2

Ҷавоб: √ а 2 + в 2

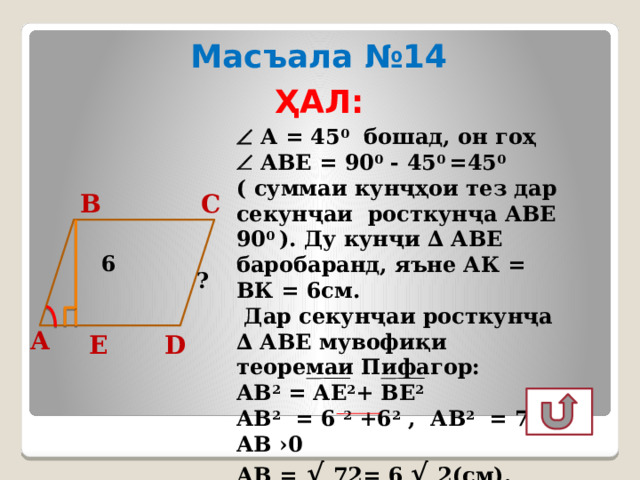
Масъала №14

ҲАЛ:

 А = 45 0 бошад, он гоҳ

 АВЕ = 90 0 - 45 0 =45 0 ( суммаи кунҷҳои тез дар секунҷаи росткунҷа АВЕ 90 0 ). Ду кунҷи ∆ АВЕ баробаранд, яъне АК = ВК = 6см.

Дар секунҷаи росткунҷа ∆ АВЕ мувофиқи теоремаи Пифагор:

АВ 2 = АЕ 2 + ВЕ 2

АВ 2 = 6 2 +6 2 , АВ 2 = 72, АВ ›0

АВ = √ 72= 6 √ 2(см).

Ҷавоб: 6 √ 2 см.

В

С

6

?

А

Е

D

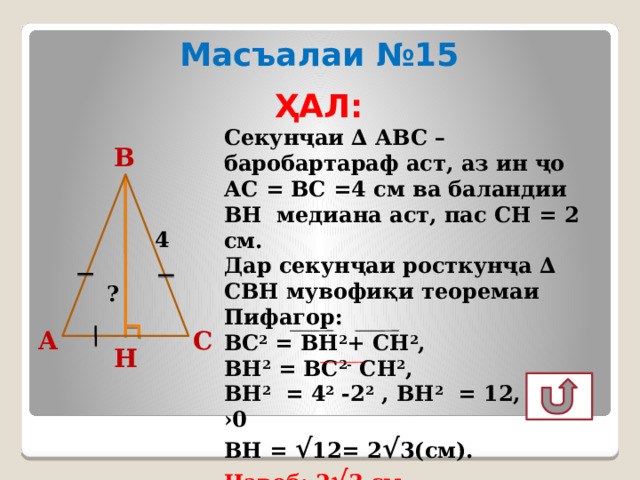
Масъалаи №15

ҲАЛ:

Секунҷаи ∆ АВС – баробартараф аст, аз ин ҷо АС = ВС =4 см ва баландии ВН медиана аст, пас СН = 2 см.

Дар секунҷаи росткунҷа ∆ СВН мувофиқи теоремаи Пифагор:

ВС 2 = ВН 2 + СН 2 ,

ВН 2 = ВС 2- СН 2 ,

ВН 2 = 4 2 -2 2 , ВН 2 = 12, ВН ›0

ВН = √ 12= 2 √ 3(см).

Ҷавоб: 2 √ 3 см.

В

4

?

С

А

Н

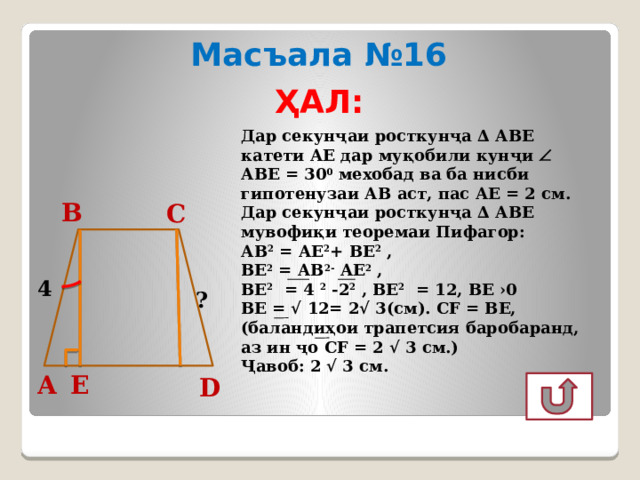
Масъала №16

ҲАЛ:

Дар секунҷаи росткунҷа ∆ АВЕ катети АЕ дар муқобили кунҷи  АВЕ = 30 0 мехобад ва ба нисби гипотенузаи АВ аст, пас АЕ = 2 см.

Дар секунҷаи росткунҷа ∆ АВЕ мувофиқи теоремаи Пифагор:

АВ 2 = АЕ 2 + ВЕ 2 ,

ВЕ 2 = АВ 2- АЕ 2 ,

ВЕ 2 = 4 2 -2 2 , ВЕ 2 = 12, ВЕ ›0

ВЕ = √ 12= 2√ 3(см). СF = ВЕ,

(баландиҳои трапетсия баробаранд, аз ин ҷо СF = 2 √ 3 см.)

Ҷавоб: 2 √ 3 см.

В

С

4

?

Е

А

D

Ҷавобатон нодуруст!

Нодуруст! Фикр кунед!

НОДУРУСТ!

Ҷавобатон нодуруст!

Дуруст!

Дуруст!

Офарин!

Дуруст!

Дуруст!

Офарин!