Теоретический материал для самостоятельного изучения

Теоретический материал для самостоятельного изучения

Лемма о перпендикулярности двух параллельных прямых к третьей прямой. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой..

Доказательство:

Дано: a ‖ b, a ⊥ c

Доказать: b ⊥ c

Через точку М пространства, не лежащую на данных прямых, проведем прямые МА и МС, параллельные соответственно прямым а и с. Так как а ⊥ с, то ∠АМС=90^о.

Так как b ‖ a, а а ‖ МА, то b ‖ МА.

Итак, прямые b и с параллельны соответственно прямым МА и МС, угол между ними равен 90^о, т.е. b ‖ МА, с ‖ МС, угол между МА и МС равен 90^о

Это означает, что угол между прямыми b и с также равен 90^о, то есть b ⊥ с. 

Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.

Доказательство:

Дано: a ‖ а₁, а ⊥ α

Доказать, что а₁ ⊥ α

Проведем какую-нибудь прямую x в плоскости α, т.е. x ∊ α.Так как а ⊥ α, то а ⊥ x.

По лемме о перпендикулярности двух параллельных прямых к третьей а₁ ⊥ x.

Таким образом, прямая а₁ перпендикулярна к любой прямой, лежащей в плоскости α, т. е. а₁ ⊥ α

Теорема. Ели две прямые перпендикулярны плоскости, то они параллельны.

Дано: а ⊥ α, b ⊥ α

Доказать, что а ‖ b

Доказательство:

Через какую-нибудь точку М прямой b проведем прямую b₁, параллельную прямой а.

М ∊ b, M ∊b₁, b₁ ‖ a. По предыдущей теореме b₁ ⊥ α.

Докажем, что прямая b₁ совпадает с прямой b. Тем самым будем доказано, что а ‖ b. Допустим, что прямые b₁ и b не совпадают. Тогда в плоскости β, содержащей прямые b и b₁, через точку М проходят две прямые, перпендикулярные к прямой с, по которой пересекаются плоскости α и β. Но это невозможно, следовательно, а ‖ b, т.е. b ∊ β, b₁ ∊ β, α   β = c (невозможно)→ а ‖ b

Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости.

Теорема. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Рис. 2.

Доказательство.

Пусть дана плоскость α и точка М (см. рис. 2). Нужно доказать, что через точку М проходит единственная прямая с, перпендикулярная плоскости α.

Проведем прямую а в плоскости α (см. рис. 3). Согласно доказанному выше утверждению, через точку М можно провести плоскость γ перпендикулярную прямой а. Пусть прямая b – линия пересечения плоскостей α и γ.

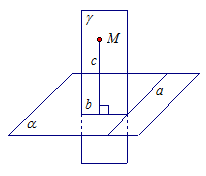
Рис. 3.

В плоскости γ через точку М проведем прямую с, перпендикулярную прямой b.

Прямая с перпендикулярна b по построению, прямая с перпендикулярна а (так как прямая а перпендикулярна плоскости γ, а значит, и прямой с, лежащей в плоскости γ). Получаем, что прямая с перпендикулярна двум пересекающимся прямым из плоскости α. Значит, по признаку перпендикулярности прямой и плоскости, прямая с перпендикулярна плоскости α. Докажем, что такая прямая с единственная.

Предположим, что существует прямая с₁, проходящая через точку М и перпендикулярная плоскости α. Получаем, что прямые с и с₁ перпендикулярны плоскости α. Значит, прямые с и с₁ параллельны. Но по построению прямые с и с₁пересекаются в точке М. Получили противоречие. Значит, существует единственная прямая, проходящая через точку М и перпендикулярная плоскости α, что и требовалось доказать.

Примеры и разборы решения заданий тренировочного модуля

Пример 1

Выбор элемента из выпадающего списка

Выпишите ребра, перпендикулярные плоскости (DC ).

• AD, A₁D₁, BC, B₁C₁

• AD, AC, AD₁,

• ВС, ВА.

Правильный вариант/варианты (или правильные комбинации вариантов):

• AD, A₁D₁, BC, B₁C₁

Неправильный вариант/варианты (или комбинации):

Все остальные

Подсказка: в кубе все углы по  . Плоскость (DC ), проходит через грань куба DC .

• Разбор задания: Куб – это геометрическая фигура у которой все углы прямые, следовательно нужно увидеть ребра которые перпендикулярны к плоскости (DC ), к грани куба (DDC ).Эти ребра - AD, A₁D₁, BC, B₁C₁

Пример 2

Ребус – соответствия.

Закончите предложение, чтобы получилось верное утверждение.

Утверждение:

• Две прямые называются перпендикулярными, если …..

• Если плоскости перпендикулярна одной из двух параллельных прямых, то она ……

Варианты ответов:

• 

• 

• параллельны

• один

• она перпендикулярна к любой прямой, лежай в этой плоскости.

• перпендикулярна плоскости.

Правильный вариант/варианты (или правильные комбинации вариантов):

Неправильный вариант/варианты (или комбинации):

Все остальные.

Подсказка:

Лемма: Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к третьей прямой.

Теорема: если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

Теоретический материал для самостоятельного изучения

Рассмотрим плоскость α и точку А, не лежащую в этой плоскости (рис. 1). Проведем через точку А прямую, перпендикулярную к плоскости α, и обозначим буквой Н точку пересечения этой прямой с плоскостью α. Отрезок АН называется перпендикуляром, проведенным из точки А к плоскости α, а точка Н — основанием перпендикуляра. Отметим в плоскости α какую-нибудь точку М, отличную от Н, и проведем отрезок AM. Он называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок НМ называется проекцией наклонной на плоскость α.

(Рис. 1)

Рассмотрим прямоугольный треугольник АМН. Сторона АН — катет, а сторона AM — гипотенуза, поэтому АН AM. Поэтому перпендикуляр, проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из той же точки к этой плоскости.

Следовательно, из всех расстояний от точки А до различных точек плоскости α наименьшим является расстояние до точки Н. Это расстояние, т. е. длина перпендикуляра, проведенного из точки А к плоскости α, называется расстоянием от точки А до плоскости α.

Стоит отметить, что в случае двух параллельных плоскостей, расстоянием между ними будет расстояние от произвольной точки одной плоскости до другой плоскости. Например, все точки потолка находятся на одинаковом расстоянии от пола. Если же прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости. В этом случае расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью. Например, все точки прямой b равноудалены от потолка комнаты.

Если мы имеем дело со скрещивающимися прямыми, то расстоянием между ними будет расстояние между одной из этих прямых и плоскостью, проходящей через другую прямую параллельно первой.

Сформулируем теорему о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

(Рис. 2)

На рисунке 2: АН — перпендикуляр к плоскости α, AM — наклонная, а — прямая, проведенная в плоскости α через точку М перпендикулярно к проекции наклонной НМ. Докажем, что прямая а перпендикулярна наклонной AM.

Рассмотрим плоскость АМН. Прямая а перпендикулярна к НМ по условию. Так как прямая а, лежит в плоскости α, а эта плоскость перпендикулярна отрезку AH, то прямая а перпендикулярна к этой плоскости. Отсюда следует, что прямая а перпендикулярна к любой прямой, лежащей в плоскости АМН, в частности прямая а перпендикулярна отрезку АМ. Теорема доказана.

Эта теорема называется теоремой о трех перпендикулярах, так как в ней говорится о связи между тремя перпендикулярами АН, НМ и AM.

Справедлива также обратная теорема: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.

Введем теперь понятие проекции произвольной фигуры на плоскость. Проекцией точки на плоскость называется основание перпендикуляра, проведенного из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если она лежит в плоскости.

Обозначим буквой F какую-нибудь фигуру в пространстве. Если мы построим проекции всех точек этой фигуры на данную плоскость, то получим фигуру F₁, которая называется проекцией фигуры F на данную плоскость (рис. 3).

(Рис. 3)

Докажем теперь, что проекцией прямой на плоскость, не перпендикулярную к этой прямой, является прямая (рис. 4).

Данную плоскость обозначим буквой α. Произвольную прямую, не перпендикулярную к плоскости, обозначим буквой а. Из какой-нибудь точки М прямой а проведем перпендикуляр МН к плоскости α и рассмотрим плоскость β, проходящую через прямую a и перпендикуляр МН. Плоскости α и β пересекаются по некоторой прямой а₁.

Докажем, что эта прямая и является проекцией прямой а на плоскость α. В самом деле, возьмем произвольную точку М₁ прямой а и проведем в плоскости β прямую М₁Н₁, параллельную прямой МН.

Так как отрезок MH перпендикуляр к плоскости α и отрезок MH параллелен М₁Н₁, то отрезок М₁Н₁ тоже перпендикулярен плоскости α.

Этим мы доказали, что проекция произвольной точки прямой а лежит на прямой а₁.

Аналогично доказывается, что любая точка прямой а₁ является проекцией некоторой точки прямой а. Следовательно, прямая а₁ — проекция прямой а на плоскость α. Что и требовалось доказать.

(Рис. 4)

Теперь введем понятие угла между прямой и плоскостью.

Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.

Примеры и разбор решения заданий тренировочного модуля

Пример 1. Докажем, что угол между φ₀ между данной прямой AM и плоскостью α является наименьшим из всех углов φ, которые данная прямая образует с прямыми, проведенными в плоскости α через точку А.

(Рис. 5)

Обозначим буквой Н основание перпендикуляра (рис. 5), проведенного из точки М к плоскости α.

Рассмотрим произвольную прямую р в плоскости α, проходящую через точку А и отличную от прямой АН.

Угол между прямыми AM и р обозначим через φ.

Докажем, что φ больше чем φ₀.

Из точки М проведем перпендикуляр MN к прямой р. Если точка N совпадает с точкой А, то φ равняется 90 градусам и поэтому φ больше чем φ 0. Рассмотрим случай, когда точки А и N не совпадают. Отрезок AM — общая гипотенуза прямоугольных

треугольников ANM и АНМ, поэтому
sinφ=MN/AM

Так как наклонная MN больше, чем перпендикуляр МН, то синус угла φ больше, чем синус угла φ₀. Поэтому угол φ больше, чем угол φ₀. Что и требовалось доказать.

Тестовый вопрос №7. Прямая AM перпендикулярна плоскости равностороннего треугольника ABC, точка H середина стороны BC. Найдите угол между прямой MH и плоскостью ABC, если AM = a, HB = a.

Решение. Искомый угол – MHA.

Рассмотрим треугольник ABC. Он равносторонний. Это означает, что его медиана так же является высотой и биссектрисой. Так как HB = a, следовательно, любая сторона треугольника имеет длину 2a. Рассмотрим треугольник AHB. Он прямоугольный, т.к. AH медиана и высота. По теореме Пифагора вычислим длину стороны AH:  .

Далее рассмотрим треугольник MHA, он прямоугольный, т.к. MA перпендикулярна плоскости ABC. Зная это мы можем выразить тангенс искомого угла:  .. Отсюда делаем вывод, что искомый угол равен 30 градусов.

Ответ: ∠MHA = 30˚.

Тестовый вопрос №8. Из точки O к плоскости α проведена наклонная, длина которой равна 17 см, проекция наклонной равна 15 см. На каком расстоянии от плоскости находится точка O?

Решение. Нарисуем рисунок. OH – перпендикуляр, OM – наклонная, длина которой 17 см, MH – проекция наклонной, длина которой 15 см.

Треугольник OHM – прямоугольный, т.к. OH – перпендикуляр. Поэтому OH – искомое расстояние. Найдем его по теореме Пифагора:   сантиметров.

Ответ: 8 сантиметров.