Зачет по геометрии учени___ 8 класса __________________________ Тема: «Подобие треугольников».
1 вариант.
Часть 1.
Определить являются ли ниже приведенные утверждения верными (да -+, нет-)
| № | Утверждение | +/- |
| 1 | Любые два прямоугольных треугольника подобны | |
| 2 | Если два угла одного треугольника соответственно пропорциональны двум углам другого треугольника, то такие треугольники подобны. | |
| 3 | Два треугольника называются подобными, если их углы соответственно равны | |
| 4 | Если два треугольника подобны, то их соответствующие стороны равны | |
| 5 | Отношение периметров двух подобных треугольников равно коэффициенту подобия | |
| 6 | Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны. | |
| 7 | Любые два прямоугольных и равнобедренных треугольника подобны. | |
| 8 | Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны | |
| 9 | Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, то такие треугольники подобны | |
| 10 | Любые два равнобедренных треугольника подобны. | |
| 11 | Высота прямоугольного треугольника равна среднему геометрическому между проекциями катетов на гипотенузу | |
| 12 | Синус острого угла прямоугольного треугольника это отношение катетов треугольника | |
| 13 | Косинус 45° не существует | |
| 14 | Диагонали трапеции при пересечении образуют четыре подобных треугольника. | |
Часть 2.
Необходимо ответить на вопросы и записать формулировку геометрического утверждения
| № | Вопрос | Ответ |
| 1 | Что такое средняя линия треугольника? | |
| 2 | Сформулируйте свойство биссектрисы треугольника | |
| 3. | Какие треугольники называются подобными? | |
| 4. | Сформулируйте признаки подобия треугольников: | 1. 2. 3. |
| 5 | Запишите теорему об отношении площадей подобных треугольников. | |
| 6 | Сформулируйте утверждение о пропорциональных отрезках в прямоугольном треугольнике. | |
| 7. | Что такое косинус острого угла прямоугольного треугольника? | |
| 8. | Записать основное тригонометрическое тождество. | |
| 9. | Косинус 45º, синус 30º,тангенс 90º | |
| 10. | Сформулировать теорему о точке пересечения медиан треугольника | |
Часть 3.
(выполнить любое из предложенных заданий)
1). Доказать любой признак подобия треугольников
2). Доказать, что высота прямоугольного треугольника, проведенная из вершины прямого угла , есть среднее геометрическое между проекциями катетов на гипотенузу.
Решить задачу:
Диагональ BD трапеции ABCD равна большему основанию AD этой трапеции и перпендикулярна к нему. Найдите площадь трапеции, если АВ=3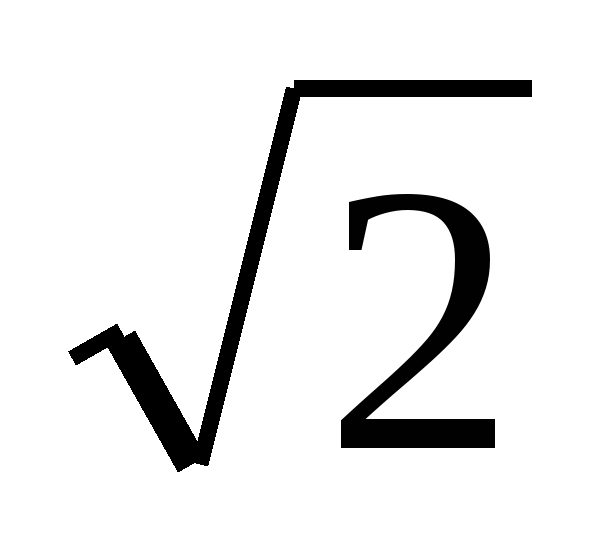 см, C=60°.
см, C=60°.
Зачет по геометрии учени __ 8 класса ______________________________
Тема: «Подобие треугольников».
2 вариант.
Часть 1.
Определить являются ли ниже приведенные утверждения верными (да -+, нет-)
| № | Утверждения | +/- |
| 1 | Любые два равнобедренных треугольника подобны. | |
| 2 | Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. | |
| 3 | Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны. | |
| 4 | Любые два равнобедренных прямоугольных треугольника подобны. | |
| 5 | Два треугольника называются подобными, если их углы соответственно пропорциональны | |
| 6 | Если два треугольника подобны, то их соответствующие стороны равны. | |
| 7 | Отношение площадей двух подобных треугольников равно коэффициенту подобия | |
| 8 | Если две стороны и угол между ними одного треугольника соответственно пропорциональны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны. | |
| 9 | Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны | |
| 10 | Любой прямоугольный и равнобедренный треугольники подобны | |
| 11 | Косинус это отношение противолежащего катета и гипотенузы | |
| 12 | Тангенс прямого угла не существует | |
| 13 | Проекция катета на гипотенузу, это отрезок гипотенузы треугольника, заключенный между основанием высоты, проведенный к гипотенузе и катетом | |
| 14 | Диагонали трапеции при пересечении образуют два подобных треугольника. | |
Часть 2.
Необходимо ответить на вопросы и записать формулировку геометрического утверждения
| № | Вопрос | Ответ |
| 1 | Сформулируйте теорему о средней линии треугольника? | |
| 2 | Запишите определение подобных треугольников | |
| 3. | Что называют коэффициентом подобия? | |
| 4. | Чему равен квадрат коэффициента подобия | |
| 5 | Сформулируйте признаки подобия треугольников: | 1. 2. 3. |
| 6 | Что такое тангенс острого угла прямоугольного треугольника | |
| 7. | Что такое синус острого угла прямоугольного треугольника | |
| 8. | Запишите значения синус  , косинус 45º, тангенс 90º , косинус 45º, тангенс 90º | |
| 9. | Сформулируйте свойство биссектрисы треугольника
| |
| 10. | Теорема о высоте прямоугольного треугольника | |
Часть 3. (выполнить любое из данных заданий)
1). Доказать любой признак подобия треугольников
2). Доказать, что высота прямоугольного треугольника, проведенная из вершины прямого угла разбивает этот треугольник на два подобных между собой треугольника.
Решить задачу:
Диагональ BD трапеции ABCD равна меньшему основанию ВС этой трапеции и перпендикулярна к нему. Найдите площадь трапеции, если CD=2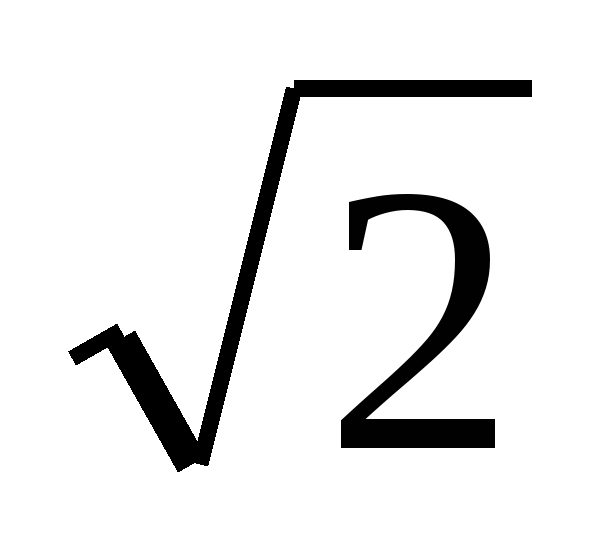 см, А=30°.
см, А=30°.
Литература и интернет ресурсы.
http://ext.spb.ru/2011-03-29-09-03-14/95-maths/2556--q-q
http://imteacher.ru (теоретические зачеты)
http://www.uchportal.ru (подобие треугольников
Фарков А.В. Теоретические тесты по геометрии 8 класс. 2012 год
Кукарцева Г.И. Сборник задач по геометрии в рисунках и тестах 7-9 класс, 2000 год)
Белицкая О.В. Геометрия 8 класс. Тесты в 2-х частях. 2012 год






 , косинус 45º, тангенс 90º
, косинус 45º, тангенс 90º

















