
«Определение вычитания и деления. Множество целых неотрицательных чисел»

Например:
Разностью чисел 7 и 3 будет число 4, т.к. 3 + 4 = 7. (7 – 3 = 4, т.к. 3 + 4 = 7).
Разность чисел 5 и 9 не существует, т.к. не существует натурального числа с, такого, что 9 + с = 5.
((5 – 9) – не сущ.,
т.к. несущ(с)( 9 + с = 5).
Вычитанием натуральных чисел a и b называют операцию, удовлетворяющую условию: а-с=в тогда и только тогда, когда в+с=а
Число а-в – называется разностью чисел а и в , число а уменьшаемым , а число в вычитаемым
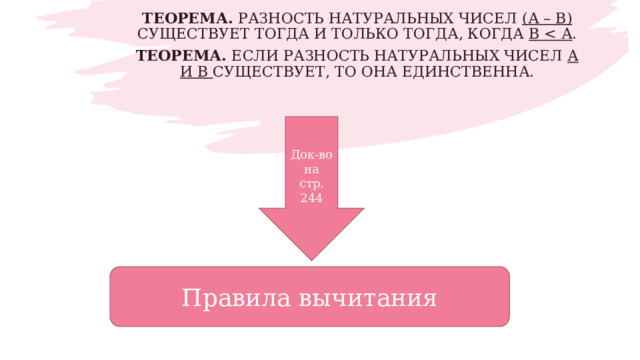
Теорема. Разность натуральных чисел (а – b) существует тогда и только тогда, когда b .
Теорема. Если разность натуральных чисел а и b существует, то она единственна.
Док-во на стр. 244
Правила вычитания
 c (a + b)– c = (a + b) – c = (a –c)+b, если a c a + (b – c) , если b c Число из суммы можно вычесть одним из трех способов: вычесть число из первого слагаемого и к полученному результату прибавить второе слагаемое. Например, (13 + 8) - 9 = (13 -9) + 8 = 4 + 8 = 12; вычесть число из второго слагаемого, и полученный результат прибавить к первому слагаемому. Например , (5 + 13) – 6 = 5 + (13 -6) = 5 + 7 = 12. найти сумму (а + b) и из нее вычесть число с. Например, (11 + 8) - 13 = 19 -13 = 6; " width="640"
c (a + b)– c = (a + b) – c = (a –c)+b, если a c a + (b – c) , если b c Число из суммы можно вычесть одним из трех способов: вычесть число из первого слагаемого и к полученному результату прибавить второе слагаемое. Например, (13 + 8) - 9 = (13 -9) + 8 = 4 + 8 = 12; вычесть число из второго слагаемого, и полученный результат прибавить к первому слагаемому. Например , (5 + 13) – 6 = 5 + (13 -6) = 5 + 7 = 12. найти сумму (а + b) и из нее вычесть число с. Например, (11 + 8) - 13 = 19 -13 = 6; " width="640"
Правило вычитания числа из суммы
s – c, где s = a + b c
(a + b)– c = (a + b) – c = (a –c)+b, если a c
a + (b – c) , если b c
Число из суммы можно вычесть одним
из трех способов:
вычесть число из первого слагаемого и к полученному результату прибавить второе слагаемое.
Например,
(13 + 8) - 9 = (13 -9) + 8 = 4 + 8 = 12;
вычесть число из второго слагаемого, и полученный результат прибавить к первому слагаемому.
Например , (5 + 13) – 6 = 5 + (13 -6) = 5 + 7 = 12.
найти сумму (а + b) и из нее вычесть число с.
Например,
(11 + 8) - 13 = 19 -13 = 6;
 b + с (a – c) – b Сумму из числа можно вычесть одним из трех способов: Из числа а вычесть второе слагаемое и из полученного результата вычесть первое слагаемое; Например: 13 – (5 + 3) = (13 – 3) – 5 = 10 – 5 = 5 из числа а вычесть первое слагаемое b, и из полученного результата (а – b) вычесть второе слагаемое с; Например: 17 – (7 + 5) = (17 – 7) – 5 = 10 – 5 = 5; найти сумму (b + с), и полученный результат вычесть из числа a; Например : 19 – (2 + 7) =19 – 9 = 10; " width="640"
b + с (a – c) – b Сумму из числа можно вычесть одним из трех способов: Из числа а вычесть второе слагаемое и из полученного результата вычесть первое слагаемое; Например: 13 – (5 + 3) = (13 – 3) – 5 = 10 – 5 = 5 из числа а вычесть первое слагаемое b, и из полученного результата (а – b) вычесть второе слагаемое с; Например: 17 – (7 + 5) = (17 – 7) – 5 = 10 – 5 = 5; найти сумму (b + с), и полученный результат вычесть из числа a; Например : 19 – (2 + 7) =19 – 9 = 10; " width="640"
Правила вычитания суммы из числа
a – s , s = b + c,
a – (b + c)= (a – b) – c, если а b + с
(a – c) – b
Сумму из числа можно вычесть одним из трех способов:
Из числа а вычесть второе слагаемое и из полученного результата вычесть первое слагаемое;
Например: 13 – (5 + 3) = (13 – 3) – 5 = 10 – 5 = 5
из числа а вычесть первое слагаемое b, и из полученного результата (а – b) вычесть второе слагаемое с;
Например: 17 – (7 + 5) = (17 – 7) – 5 = 10 – 5 = 5;
найти сумму (b + с), и полученный результат вычесть из числа a;
Например : 19 – (2 + 7) =19 – 9 = 10;
 S2 (а + b)-(с + d) = (а – с) + (b – d), если а с, b d; (а - d) + (b – с), если а d, b с. Например , (7+ 8) – (4+ 9) = 15 – 13 = 2; (7 + 4) – (5 + 3) = (7 – 5) + (4 – 3) = 2 + 1 = 3; (6 + 8) – (7 + 4) = (6 – 4) + (8 – 7) = 2 + 1 = 3. Правило вычитания суммы из суммы " width="640"
S2 (а + b)-(с + d) = (а – с) + (b – d), если а с, b d; (а - d) + (b – с), если а d, b с. Например , (7+ 8) – (4+ 9) = 15 – 13 = 2; (7 + 4) – (5 + 3) = (7 – 5) + (4 – 3) = 2 + 1 = 3; (6 + 8) – (7 + 4) = (6 – 4) + (8 – 7) = 2 + 1 = 3. Правило вычитания суммы из суммы " width="640"
S1 – S2, если S1=a + b, S2 = с + d и S1 S2
(а + b)-(с + d) = (а – с) + (b – d), если а с, b d;
(а - d) + (b – с), если а d, b с.
Например ,
(7+ 8) – (4+ 9) = 15 – 13 = 2;
(7 + 4) – (5 + 3) = (7 – 5) + (4 – 3) = 2 + 1 = 3;
(6 + 8) – (7 + 4) = (6 – 4) + (8 – 7) = 2 + 1 = 3.
Правило вычитания суммы из суммы

Например:
Частным чисел 42 и 7 будет число 6, т.к. 7 * 6 = 42,
(42 : 7 = 6, т.к. 7 * 6 = 42).
Частное чисел 15 и 7 не существует, т.к. не существует такого натурального числа с, что 7*с = 15
Делением натуральных чисел а и b называют операция, удовлетворяющая условию: а: b = с тогда и только тогда, когда b*с = а
Число а:в называется частным чисел а и в , число а – делимым, число в - делителем
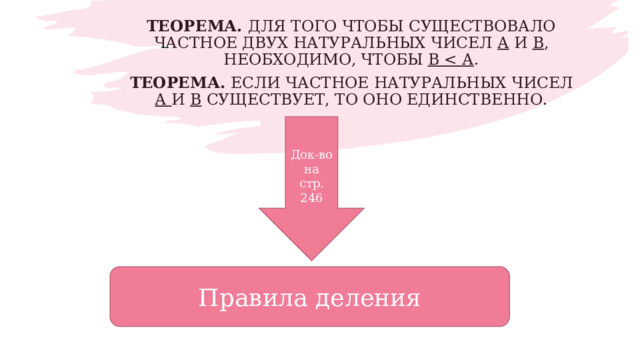
Теорема. Для того чтобы существовало частное двух натуральных чисел а и b , необходимо, чтобы b .
Теорема. Если частное натуральных чисел а и b существует, то оно единственно.
Док-во на стр. 246
Правила деления

Правило деления суммы на число
Теорема .
Если числа а и b делятся на число с , то их сумма а + b делится на с , причем частное, получаемое при делении суммы а + b на число с , равно сумме частных получаемых при делении а на с и b на с, т.е.,
(а + b):с = а:с + b:с.
Например , (60 + 16): 2 = 60 : 2 + 16 : 2 = 38.
Эту теорему можно сформулировать в виде правила: для того чтобы разделить сумму на число, достаточно разделить на это число каждое из слагаемых и полученные результату сложить
 b , то разность а – b делится на с , причем частное, получаемое при делении разности на число с , равно разности частных, получаемых при делении а на с и b на с , т.е., (а – b): с = а : с – b : с. Например , (36 – 27) : 3 = 36 : 3 – 27 : 3 = 12 – 9 = 3. Эту теорему можно сформулировать в виде правила: для того чтобы разделить разность на число, достаточно разделить на это число уменьшаемое и вычитаемое, а затем из первого частного вычесть второе. " width="640"
b , то разность а – b делится на с , причем частное, получаемое при делении разности на число с , равно разности частных, получаемых при делении а на с и b на с , т.е., (а – b): с = а : с – b : с. Например , (36 – 27) : 3 = 36 : 3 – 27 : 3 = 12 – 9 = 3. Эту теорему можно сформулировать в виде правила: для того чтобы разделить разность на число, достаточно разделить на это число уменьшаемое и вычитаемое, а затем из первого частного вычесть второе. " width="640"
Правило деления разности на число
Теорема.
Если натуральные числа а и b делятся на число с и а b , то разность а – b делится на с , причем частное, получаемое при делении разности на число с , равно разности частных, получаемых при делении а на с и b на с , т.е.,
(а – b): с = а : с – b : с.
Например , (36 – 27) : 3 = 36 : 3 – 27 : 3 = 12 – 9 = 3.
Эту теорему можно сформулировать в виде правила:
для того чтобы разделить разность на число, достаточно разделить на это число уменьшаемое и вычитаемое, а затем из первого частного вычесть второе.

Правило деления произведения на число
Теорема.
Если натуральное число а делится на натуральное число с , то для любого натурального числа b произведение аb делится на с . При этом частное, получаемое при делении произведения аb на число с , равно произведению частного, получаемого при делении а на с ,
т.е. (а*b): с = (а : с) * b.
Например , (6 *115) : 3 = (6 : 3) *115 = 230.
Теорему можно сформулировать в виде правила: для того чтобы разделить произведение на число, достаточно разделить на это число один из множителей и полученный результат умножить на второй множитель.

Задание:
- Определите значение выражения, не выполняя письменных вычислений:
7865⋅6-7865⋅5
957⋅11-957
12⋅36-7⋅36



Домашнее задание:









 c (a + b)– c = (a + b) – c = (a –c)+b, если a c a + (b – c) , если b c Число из суммы можно вычесть одним из трех способов: вычесть число из первого слагаемого и к полученному результату прибавить второе слагаемое. Например, (13 + 8) - 9 = (13 -9) + 8 = 4 + 8 = 12; вычесть число из второго слагаемого, и полученный результат прибавить к первому слагаемому. Например , (5 + 13) – 6 = 5 + (13 -6) = 5 + 7 = 12. найти сумму (а + b) и из нее вычесть число с. Например, (11 + 8) - 13 = 19 -13 = 6; " width="640"
c (a + b)– c = (a + b) – c = (a –c)+b, если a c a + (b – c) , если b c Число из суммы можно вычесть одним из трех способов: вычесть число из первого слагаемого и к полученному результату прибавить второе слагаемое. Например, (13 + 8) - 9 = (13 -9) + 8 = 4 + 8 = 12; вычесть число из второго слагаемого, и полученный результат прибавить к первому слагаемому. Например , (5 + 13) – 6 = 5 + (13 -6) = 5 + 7 = 12. найти сумму (а + b) и из нее вычесть число с. Например, (11 + 8) - 13 = 19 -13 = 6; " width="640"
 b + с (a – c) – b Сумму из числа можно вычесть одним из трех способов: Из числа а вычесть второе слагаемое и из полученного результата вычесть первое слагаемое; Например: 13 – (5 + 3) = (13 – 3) – 5 = 10 – 5 = 5 из числа а вычесть первое слагаемое b, и из полученного результата (а – b) вычесть второе слагаемое с; Например: 17 – (7 + 5) = (17 – 7) – 5 = 10 – 5 = 5; найти сумму (b + с), и полученный результат вычесть из числа a; Например : 19 – (2 + 7) =19 – 9 = 10; " width="640"
b + с (a – c) – b Сумму из числа можно вычесть одним из трех способов: Из числа а вычесть второе слагаемое и из полученного результата вычесть первое слагаемое; Например: 13 – (5 + 3) = (13 – 3) – 5 = 10 – 5 = 5 из числа а вычесть первое слагаемое b, и из полученного результата (а – b) вычесть второе слагаемое с; Например: 17 – (7 + 5) = (17 – 7) – 5 = 10 – 5 = 5; найти сумму (b + с), и полученный результат вычесть из числа a; Например : 19 – (2 + 7) =19 – 9 = 10; " width="640"
 S2 (а + b)-(с + d) = (а – с) + (b – d), если а с, b d; (а - d) + (b – с), если а d, b с. Например , (7+ 8) – (4+ 9) = 15 – 13 = 2; (7 + 4) – (5 + 3) = (7 – 5) + (4 – 3) = 2 + 1 = 3; (6 + 8) – (7 + 4) = (6 – 4) + (8 – 7) = 2 + 1 = 3. Правило вычитания суммы из суммы " width="640"
S2 (а + b)-(с + d) = (а – с) + (b – d), если а с, b d; (а - d) + (b – с), если а d, b с. Например , (7+ 8) – (4+ 9) = 15 – 13 = 2; (7 + 4) – (5 + 3) = (7 – 5) + (4 – 3) = 2 + 1 = 3; (6 + 8) – (7 + 4) = (6 – 4) + (8 – 7) = 2 + 1 = 3. Правило вычитания суммы из суммы " width="640"



 b , то разность а – b делится на с , причем частное, получаемое при делении разности на число с , равно разности частных, получаемых при делении а на с и b на с , т.е., (а – b): с = а : с – b : с. Например , (36 – 27) : 3 = 36 : 3 – 27 : 3 = 12 – 9 = 3. Эту теорему можно сформулировать в виде правила: для того чтобы разделить разность на число, достаточно разделить на это число уменьшаемое и вычитаемое, а затем из первого частного вычесть второе. " width="640"
b , то разность а – b делится на с , причем частное, получаемое при делении разности на число с , равно разности частных, получаемых при делении а на с и b на с , т.е., (а – b): с = а : с – b : с. Например , (36 – 27) : 3 = 36 : 3 – 27 : 3 = 12 – 9 = 3. Эту теорему можно сформулировать в виде правила: для того чтобы разделить разность на число, достаточно разделить на это число уменьшаемое и вычитаемое, а затем из первого частного вычесть второе. " width="640"






















