Теория вероятности, случайные события

№

Деятельность учителя

(с обозначением используемых технологий, методов, приемов; применяемого технического оснащения)

Деятельность обучающихся

(с обозначением видов и форм активности)

Планируемый результат,

комментарии

1 этап - Организационный момент- 3 мин.

1.1.

– Добрый день, дорогие ребята, уважаемые гости.

- Наш урок сегодня я хочу начать со слов Джона Локка

Слайд №1

«Никто не знает силы способностей,

пока не использует их».

– Ребята, хочу пожелать вам сегодня каждому узнать силу своих способностей и использовать их на этом уроке.

- Вы уже обратили внимание на мой рабочий стол, на нем не совсем инструменты учителя.

- Может быть, кто то из вас встречал и знает тему в математике с такими рабочими инструментами?

- «Пока я шла к вам на урок, я встретила завуча». Пример чего я вам привела?

- Да наука математика обнаружила интересные закономерности, которые позволяют человеку увереннее чувствовать себя при встрече со случайными событиями.

Какие события вы еще знаете?

Какие действия с этими событиями мы можем делаем?

- Как вы думаете, какова цель нашего урока, если дальше я попрошу показать вас на примере решения задач, как применять правила нахождения вероятностей случайных событий и обобщить полученные ранее знания?

- Кто может сообщить тему урока?

Запись дату и тему урока

– У каждого из вас есть на столах оценочные листы. Подпишите их. На них будут выставляться баллы за проделанные виды работ на уроке.

Приветствуют учителя,

Включаются в деловой ритм урока.

Слушают.

Теория вероятностей

Случай, случайные события

Достоверные, невозможные, совместные, несовместные, противоположные, равновозможные.

Описываем, анализируем, оцениваем, рассчитываем вероятность…

Повторить, закрепить и систематизировать изученный материал

Обобщающий урок по теме «Теория вероятности, случайные события».

Запись дату и тему урока

Подписывают листы оценивания.

Создать благоприятный психологический настрой на работу.

Личностные: формирование ответственного отношения к выполнению домашнего задания.

Регулятивные: фиксация индивидуального затруднения, самооценка

1.2.

- Как вы справились с домашним заданием? В чем были затруднения? Слайд №2

Проверяют домашнее задание по слайду, задают вопросы при возможных затруднениях.

2 этап – Актуализация знаний - 10 мин.

2.1.

 -Какое событие называется случайным (достоверным, невозможным, совместным, несовместным).

- Чему равна вероятность этих события?

Слайд №3

Событие, которое происходит всегда, называют достоверным
Событие, которое не может произойти, называется невозможным.

(Пусть из урны, содержащей

только черные шары, вынимают шар. Тогда появление черного шара –

достоверное событие;

Появление белого

шара – невозможное событие)

Два события, которые в данных условиях могут происходить одновременно, называются совместными, а те, которые не могут происходить одновременно, - несовместными.

(Брошена монета. Появление «герба» исключает появление надписи. События «появился герб» и «появилась надпись» - несовместные.)

0

Р (А)=1(достоверное событие А)

Р (А)=0 (невозможное событие А)

Актуализация опорных знаний и способов действий

Коммуникативные:

аргументация своих ответов.

Познавательные:

осознанное построение речевого высказывания, подведение под понятие.

Регулятивные:

осуществление действий контроля.

2.2.

- Предлагает выполнить «Устный счёт», за каждую решенную задачу вы получаете заработанные баллы, но не забывайте их в оценочный лист

Слайд №4

- Перенесите заработанные баллы в оценочный лист

Работают индивидуально, ответы записывают в листы оценивания

После выполнения проверка по готовым ответам

В листы оценивания заносят баллы за устный счёт.

2.3.

- Предлагает вспомнить классическое определение вероятности

(говорят, потом слайд)

(слайд 5)

- Давайте вместе вспомним алгоритм решения задач с помощью классического определения вероятности

Слайд 6

слайд 7

- Перед вами Задача1 и вопрос

В портфеле лежат 4 книги: математика, русский язык, история России и сборник по физике. Из портфеля наугад вынимается книга. Какова вероятность вытащить учебник математики?

-Отлично, не забывайте оценивать решенную задачу по критериям оценочного листа.

Задача 2.

(слайд 8)

В среднем из 100 карманных фонариков, поступивших в продажу, 5 неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен

- Давайте вспомним правила с равновероятностными событиями?

(Говорят, потом слайд)

(слайд 9)

- Предлагаю решить Задачу 3 и ответьте на вопросы

(слайд 10)

Из карточек составили слово «пирамида».

-Какую карточку с буквой вероятнее всего вытащить?

-Отлично, не забывайте заносить баллы

Классическое определение вероятности:

Вероятностью P события А при проведении некоторого испытания называют отношение числа тех исходов, в результате которых наступает событие А (m – число благоприятных исходов), к общему числу всех (равновозможных между собой) исходов этого испытания (n – число всех возможных исходов).

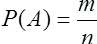
Алгоритм для решения задач с помощью классического определения.

1)обозначить событие (А)

2)сосчитать число всех исходов (n)

3)сосчитать число исходов благоприятствующих данному событию (m)

4)найти отношение благоприятствующих исходов к числу всех исходов

Число всех исходов 4(п).

Благоприятствующих исходов 1(m);

Вероятность события Р(А)= 1/4= 0,25

Число всех исходов 100(п).

Благоприятствующих исходов 95 (m);

Вероятность события Р(А)= 95/100= 0,95

Сложение и умножение вероятностей, повторяют правила

Вероятность Р(С) наступления хотя бы одного из двух несовместных событий А и В равна сумме их вероятностей.

Р(С) = Р(А + В) = Р(А) + Р(В)

Вероятность противоположного события Р(А) = 1 - Р(А).

Вероятность Р(С) совместного наступления двух независимых событий А и В равна произведению вероятностей событий А и В.

Р(С) = Р(А)· Р(В)

Всего 8 букв.

Буква «и» встречается 2 раза – P = 2/8= 1/4;

буква «а» встречается 2 раза – P= 2/8= 1/4;

остальные 1 раз– P = 1/8.

В листы оценивания заносят баллы за устный счёт.

3 этап – Систематизация изученного материала - 20 мин.

3.1.

В конце учебного года вам предстоит пройти Государственную Итоговую Аттестацию в форме ОГЭ встречаются ли заданиями с «Теорией вероятности, случайных событий» текстах по математике?

Слайд №11

Предлагаю вам выполнить Самостоятельную работу по типовым текстам открытого банка задач ФИПИ. На работу у вас 12-15 минут

-В рабочих тетрадях записываете решение и ответ.

- Давайте проверим решение и сверим ваши ответы.

Слайде №12

- У кого задания вызвали затруднения?

- В чем причина?

- У кого задания выполнены правильно?

- Заполняем оценочный лист.

1) Решают задачи

2) Записывают решение в тетради

3) Смотрят на слайд и слушают выступление своих одноклассников

Сверяют записи со слайдом

Выставляют баллы в оценочный лист.

Личностные: осознание ответственности за общее дело.

Познавательные:

выполнение действий по алгоритму. Подведение под понятие, рефлексия способов действий

Коммуникативные: выражение своих мыслей, достижение договоренности и согласование общего решения

4 этап – Физкультминутка - 2 мин

4.1.

– Сейчас проверим, насколько вы разбираетесь в классификации событий. Проведем подвижную паузу в виде викторины.

- Оцените возможность наступления событий, используя для этого следующие действия:

Слайд №13

«достоверное событие»

(все сидят и не встают), «случайное событие»

(поднять руку),

«невозможное событие» (должны встать).

1: «завтра будет хорошая погода».

2: «в январе в поселке пойдет снег».

3: «в 12 часов в поселке идет дождь, а через 24 часа будет светить солнце».

4: «на день рождения вам подарят говорящего крокодила».

5: «круглая отличница получит двойку».

6: «камень, брошенный в воду, утонет».

7: «вы выходите на улицу, а навстречу идет слон».

8: «вас пригласят лететь на Луну».

9: «вы не выиграете, участвуя в беспроигрышной лотерее».

10: «после четверга будет пятница».

Слушают.

Выполняют викторину.

1. Поднимают руку.

2. Все сидят и не встают.

3. Поднимают руку.

4. Встают.

5. Поднимают руку.

6. Все сидят и не встают.

7. Встают.

8. Поднимают руку.

9. Встают.

10. Все сидят и не встают.

Ориентируются в своей системе знаний;

проводят анализ учебного материала

1. этап - Домашнее задание - 2 мин

5.1

- Предлагает домашнее задание на карточках – это типовые задание ОГЭ

Комментирование д/з

Получают карточки с заданием.

Задают вопросы по домашнему заданию

Планирование, Самоопределение.

6 этап - Рефлексия учебной деятельности на уроке - 5 мин.

Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что подлежит усвоению, осознание качества и уровня усвоения.

Познавательные: анализ, подведение под понятие, рефлексия способов действия, формирование адекватного понимания причин успеха и оценка процесса и результатов деятельности

Коммуникативные: умение выражать свои мысли, аргументация

Самооценка результатов своей деятельности

6.1

Слайд 14

- Какую цель мы ставили в начале урока?

-Наша цель достигнута?

- Ребята, скажите, Вы узнали силы своих способностей, которые вы использовали на этом уроке?

У меня на столе остался еще один случайный предмет, который ждет количество набранных вами баллов.

Слайд 15

- Подсчитайте количество набранных баллов и поставьте соответствующие оценки;

Критерии оценки:

22-26 баллов оценка «5»

21-18 баллов оценка «4»

17-12 баллов оценка «3»

11 и меньше баллов оценка «2»

(-Узнать какое количество баллов получилось)

- Вручить «Эликсир силы» для сдачи ОГЭ)

− Оцените свою деятельность на уроке: поднимите руку, если вы поняли, как находить вероятность событий,

или не поднимайте, если не всё понятно.

Слайде №16

- Спасибо всем за работу

- Удачи на ОГЭ

Повторить, закрепить и систематизировать изученный материал

Анализируют свою работу

Оценивают результат своей работы на уроке.

Заполняют лист самооценки.

Суммируют баллы за урок, ставят себе оценку

Устный счет

Задача

1

Задача 2

Задача 3

Самостоятельная работа

Итого

Верное решение и ответ – 2балла

Вычислительная ошибка – 1 бал

Нет решения, нет ответа - 0 баллов

Задача1: __________

Задача 2: __________

Задача 3:__________

Задача 4:__________

Задача 5:__________

Задача1: __________

Задача 2: __________

Задача 3:__________

Задача 4:__________

Задача 5:__________